↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Transformers’ success in language modeling stems from combining contextual and global knowledge, but the underlying mechanisms remain unclear. Existing research often lacks rigorous analysis of training dynamics and sample complexity. This makes it difficult to design efficient training algorithms.
This paper addresses these issues by introducing the Sparse Contextual Bigram (SCB) model, a simplified yet informative model for studying transformers’ learning capabilities. The researchers used a one-layer linear transformer with a gradient-based algorithm to analyze training dynamics and sample complexity of SCB. They provide theoretical convergence and sample complexity guarantees, showing that training can be divided into a sample-intensive initial stage and a more sample-efficient later stage. Furthermore, they demonstrate how transfer learning can be used to bypass the initial intensive stage if a sufficient correlation exists between the pretraining and downstream tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers theoretical insights into the training dynamics of transformers, a widely used deep learning architecture. Understanding these dynamics is key to improving model training efficiency and generalization capabilities. The work introduces a novel minimalist model and provides rigorous convergence and sample complexity analysis, paving the way for more efficient and effective transformer training methods.
Visual Insights#
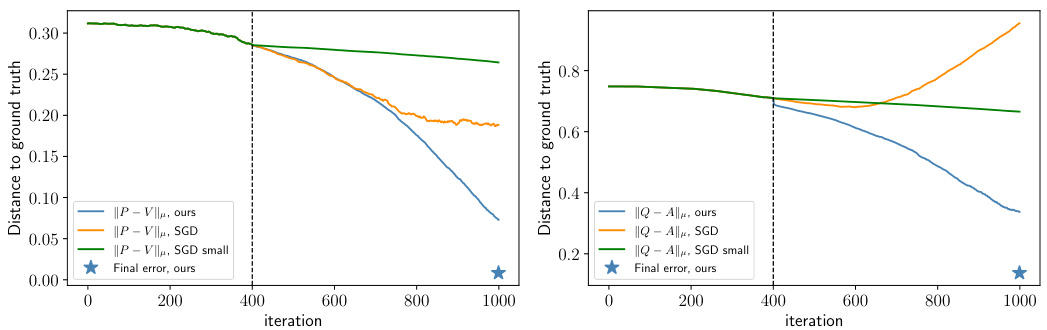
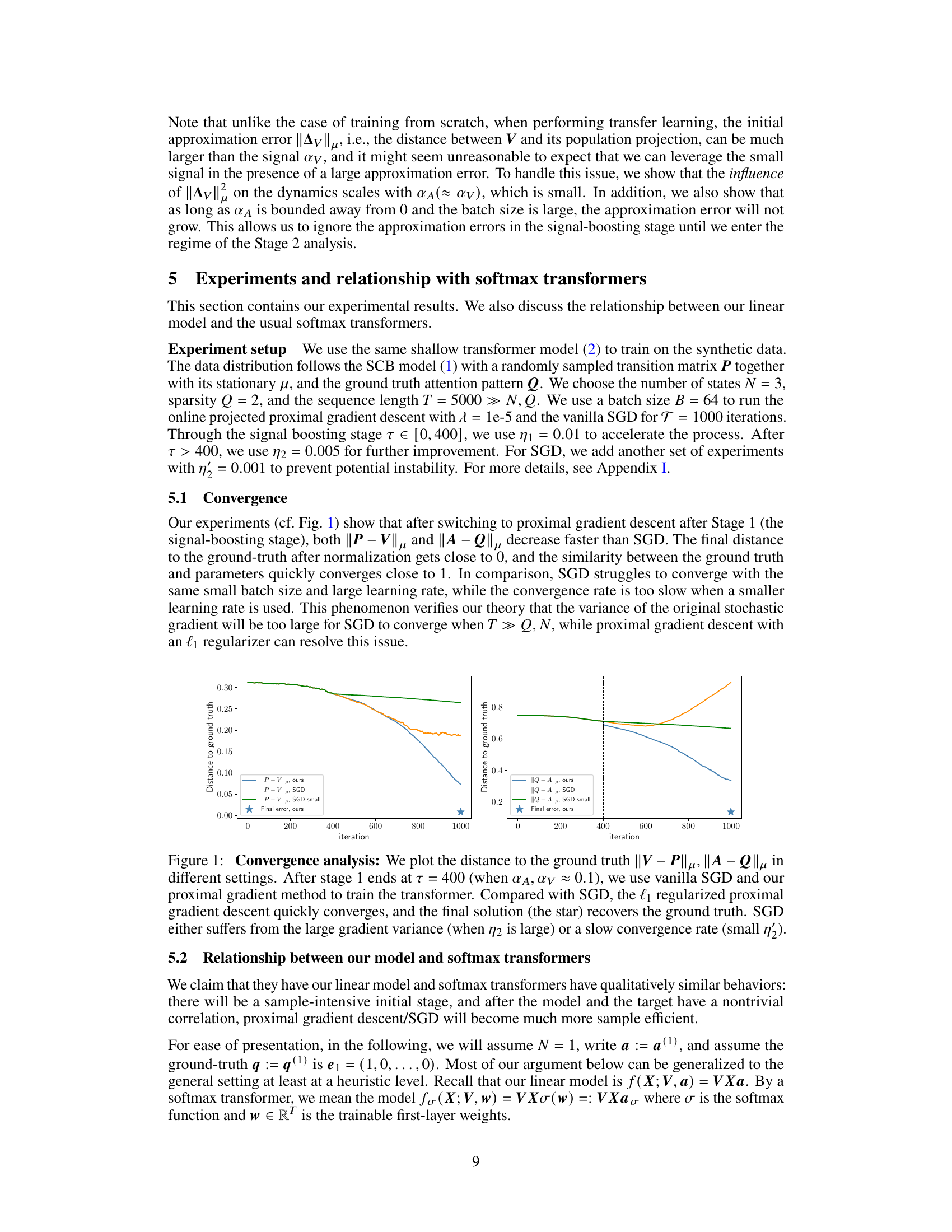
This figure compares the convergence speed of the proposed l1-regularized proximal gradient descent method and vanilla SGD for training a one-layer linear transformer on the Sparse Contextual Bigram (SCB) task. The plots show the distances to the ground truth for both the transition matrix (P) and the attention matrix (Q). It demonstrates that the proposed method significantly outperforms SGD, achieving faster convergence and a much closer approximation of the ground truth. This difference in performance is attributed to the proposed method’s ability to manage the large variance in the gradients that occur with SGD, which hinders its convergence in this specific setting.
In-depth insights#
SCB Model Intro#
The introduction of the Sparse Contextual Bigram (SCB) model is crucial to understanding the paper’s core contribution. It presents a minimalist yet insightful approach to modeling language generation, extending the traditional bigram model. The SCB model’s key innovation lies in incorporating sparse contextual information, where the next word’s prediction depends on a small subset of previous words, determined by the current word. This sparsity makes the model theoretically tractable, allowing for analysis of its training dynamics and sample complexity. The SCB model’s design elegantly bridges in-context learning and global knowledge representation, two key aspects of transformer success. By explicitly modeling contextual dependence alongside transition probabilities, it provides a framework for studying how these two abilities interact in transformer models. Analyzing the learning dynamics of the SCB model with a simple linear transformer offers valuable theoretical insights into the workings of more complex models and clarifies some of the mystery surrounding the success of transformers.
Training Dynamics#
The training dynamics of deep learning models, especially transformers, are complex and not yet fully understood. Analyzing these dynamics is crucial for improving model performance and generalization. This involves examining how model parameters change over time during training, including the effects of optimization algorithms, initialization strategies, and data characteristics. A key area of research is understanding how models learn representations and how these representations evolve during training. Understanding training dynamics can lead to more efficient training procedures, better model architectures, and a deeper comprehension of the underlying learning mechanisms. The theoretical analysis of training dynamics often involves simplifying model architectures or focusing on specific aspects of training, offering valuable insights while needing further exploration to cover the full complexity of real-world scenarios. Empirical studies, using visualization tools and metrics such as loss curves and activation patterns, are also important for complementing theoretical work. Investigating the effects of various hyperparameters on training dynamics is also important to guide the selection of optimal training settings for improved model performance.
Transfer Learning#
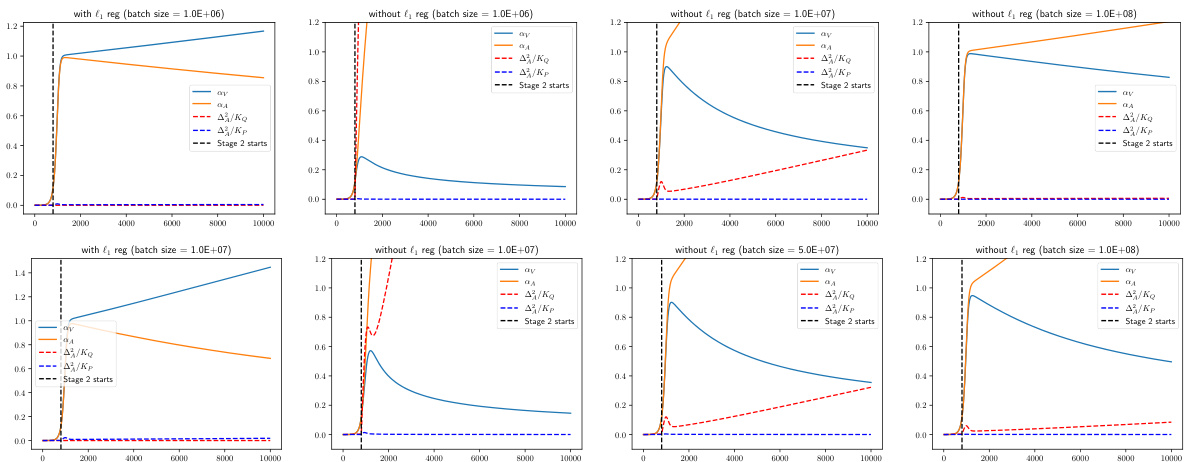
The study’s section on ‘Transfer Learning’ investigates leveraging pre-trained models to enhance the learning process for a new, downstream task. A key finding is that even with a weak correlation between the pre-training and downstream tasks, transferring a pre-trained model can significantly improve efficiency. This is achieved by bypassing the initial, sample-intensive phase of training that is required when learning from scratch. The theoretical analysis demonstrates the conditions under which transfer learning can successfully lead to accelerated convergence and reduced sample complexity. This is a significant advancement because it demonstrates that the benefits of transfer learning extend beyond cases with strong task similarity, thus broadening the scope and potential of this powerful technique. The work also underscores the importance of the relationship between model initialization and convergence speed, which is crucial for understanding and optimizing the training of deep learning models.
Softmax Link#
A hypothetical ‘Softmax Link’ in a research paper likely refers to a mechanism connecting a linear transformation to a probability distribution. This implies a crucial role in converting raw model outputs into meaningful predictions, as softmax is a standard way to normalize values into probabilities. The paper might explore how this specific link impacts the model’s behavior—for example, examining its effect on training dynamics or interpretability. An in-depth analysis would likely involve a mathematical study of the softmax function’s properties, how the link interacts with the model’s other components (like attention), and what specific advantages or disadvantages this softmax-based connection might offer compared to alternative methods for probability estimation. A key focus could be on evaluating the impact of the softmax link on model accuracy and computational efficiency. The authors might also compare the softmax link to other approaches for probability generation, offering detailed performance comparisons and theoretical justifications. Ultimately, a thorough investigation of this link would be vital for fully understanding the workings of the model described.
Future Work#
Future research directions stemming from this work could explore extending the Sparse Contextual Bigram (SCB) model to generate longer sequences, moving beyond the single-token prediction limitation. Investigating the impact of different sparsity patterns and attention mechanisms on model performance and generalization is another crucial avenue. A rigorous theoretical analysis of softmax-based transformers, drawing parallels with the SCB model, could provide deeper insights into the training dynamics and capabilities of these widely used architectures. Finally, empirical evaluations on more diverse and realistic language modeling tasks, such as machine translation or text summarization, would validate the theoretical findings and showcase the practical applicability of the proposed approach.
More visual insights#
More on figures
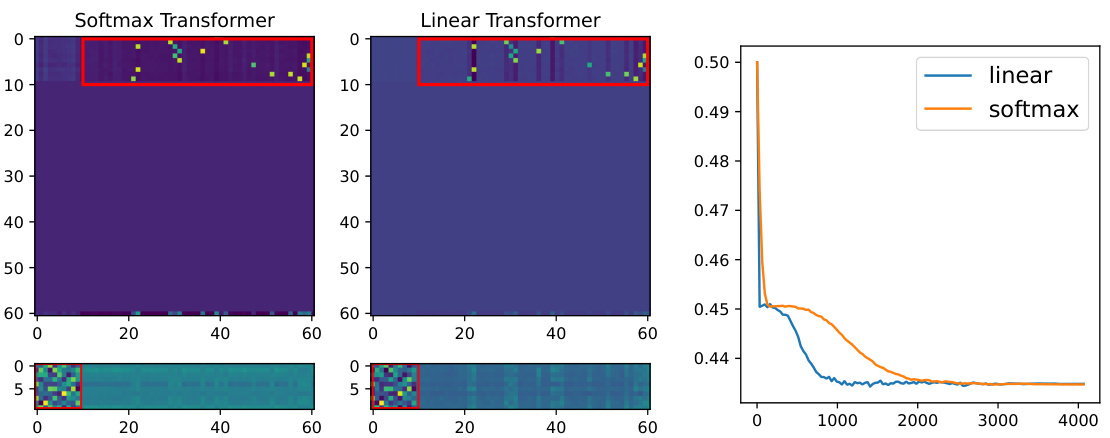
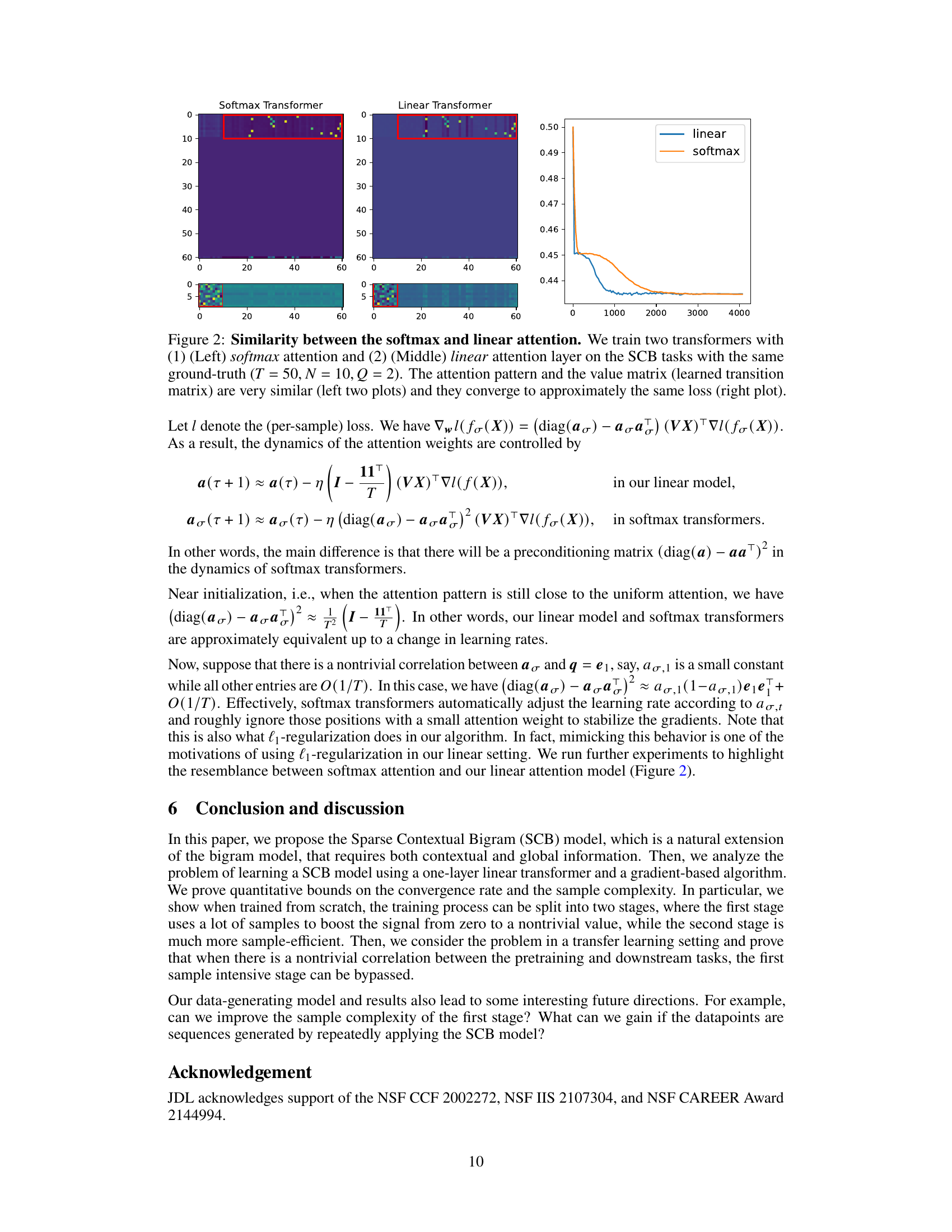
This figure compares the attention patterns and value matrices learned by softmax and linear transformers on the Sparse Contextual Bigram (SCB) task. The left and middle panels show heatmaps of the attention patterns learned by each model type. The right panel shows the training loss curves for each model. The results indicate that the attention patterns and value matrices are similar between the softmax and linear transformers, and both models converge to similar loss values.

This figure compares the convergence speed of the proposed l1-regularized proximal gradient descent method and the vanilla SGD method for training a one-layer linear transformer on the Sparse Contextual Bigram (SCB) task. The plot shows that the proximal gradient descent method converges much faster and more accurately to the ground truth than the SGD method, achieving near-perfect recovery. The SGD method’s performance is hampered by high variance with larger learning rates, while smaller learning rates result in significantly slower convergence.
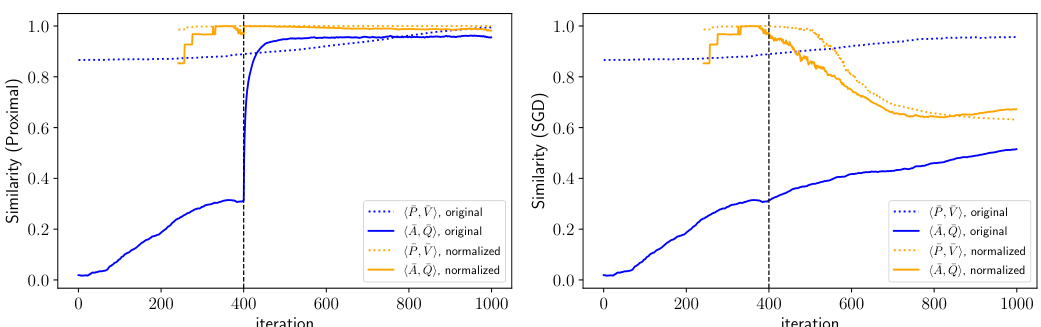
This figure compares the convergence speed of the proposed l1-regularized proximal gradient descent method and vanilla SGD in learning the Sparse Contextual Bigram (SCB) model. The results show that the proposed method significantly outperforms SGD, achieving faster convergence to the ground truth, while SGD struggles with either high variance or slow convergence rate.

This figure shows the convergence comparison of the proposed algorithm and the vanilla SGD for learning the SCB task. The proposed algorithm significantly outperforms the SGD in terms of convergence speed and accuracy. This demonstrates the effectiveness of using preconditioning and l₁-regularization in the training process.
This figure compares the convergence speed of the proposed proximal gradient descent method and the vanilla SGD method for training a one-layer linear transformer on the Sparse Contextual Bigram (SCB) task. The plot shows the distance to the ground truth for both the transition matrix (P) and the attention matrix (Q) over training iterations. The results demonstrate that the proximal gradient descent method converges significantly faster and more accurately to the ground truth than SGD, which struggles with either high variance or slow convergence.
Full paper#