↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Sharpness-Aware Minimization (SAM) is a popular optimization technique for training deep neural networks that improves generalization. However, its convergence properties lacked rigorous theoretical understanding. This created a knowledge gap, hindering our ability to fully leverage SAM’s potential and develop improved variants. Previous studies offered incomplete convergence results.
This paper bridges this gap by providing a comprehensive convergence analysis of SAM and its normalized variants. The authors establish fundamental convergence properties like stationarity of accumulation points and gradient convergence to zero. Their analysis framework is quite general, encompassing several efficient SAM versions, and shows the significance of diminishing step sizes for robust convergence, supporting the practical implementation of SAM. The findings confirm the method’s efficiency and pave the way for future improvements and the development of more advanced optimization algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides the first comprehensive convergence analysis of Sharpness-Aware Minimization (SAM) and its variants. This addresses a major gap in the theoretical understanding of a widely used optimization method, impacting the design and application of SAM across various fields.
Visual Insights#
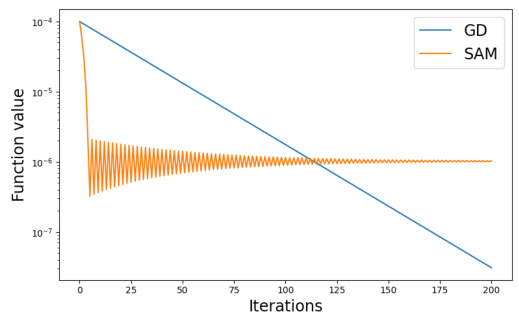
This figure shows a comparison of the convergence behavior of Gradient Descent (GD) and Sharpness-Aware Minimization (SAM) with a constant stepsize when applied to a strongly convex quadratic function. The x-axis represents the number of iterations, and the y-axis represents the function value. The plot demonstrates that while GD converges smoothly to the optimal solution, SAM with a constant stepsize fails to converge and oscillates around a suboptimal point. This highlights the need for alternative stepsize rules, such as diminishing stepsizes, in SAM to ensure convergence.

This table lists five fundamental convergence properties for smooth optimization methods. The properties describe the convergence behavior of iterates (xk), gradients (∇f(xk)), and function values (f(xk)) to a stationary point. They range from the weakest condition (lim inf ||∇f(xk)||=0) to the strongest (convergence of the sequence of iterates to a stationary point). Understanding these properties helps in comparing and analyzing the performance of different optimization algorithms.
In-depth insights#
SAM Convergence#
The convergence analysis of Sharpness-Aware Minimization (SAM) is a complex issue. Early analyses struggled to establish fundamental convergence properties, such as the convergence of gradients to zero or the convergence of function values to the optimum, particularly for non-convex functions and with constant step sizes. A significant contribution was the development of a unified framework that demonstrated these convergence properties under less restrictive conditions. The analysis extends to several normalized variants of SAM, showing convergence even with diminishing perturbation radii. However, some limitations remain. The theoretical analysis does not always translate directly to practical implementations, where aspects like scheduler choice and the non-monotone nature of the function values present challenges. Furthermore, the analysis is primarily deterministic and future work could explore stochastic versions, providing a more comprehensive and applicable understanding of SAM’s behavior in real-world scenarios.
IGD Framework#
An IGD (Inexact Gradient Descent) framework offers a flexible and powerful lens through which to analyze optimization algorithms, especially those involving approximations or noise, like Sharpness-Aware Minimization (SAM). The core idea is to relax the strict requirement of using the exact gradient at each iteration, allowing for inexact gradient calculations within a specified error bound. This approach is particularly relevant for SAM because it inherently involves perturbation, introducing an element of inexactness. An IGD framework provides a theoretical foundation to analyze the convergence behavior of SAM variants, including both normalized and unnormalized versions, despite the inherent error introduced by the perturbation strategy. By framing SAM within the IGD framework, the analysis can be extended to other methods with similar characteristics, providing a unifying theoretical perspective and potentially enabling further generalizations and improvements of gradient-based optimization techniques. A crucial aspect is the manner in which the error bound is defined (absolute vs relative), and how it interacts with the step size selection This influences the convergence rate and affects the applicability of various convergence results. Therefore, a well-defined IGD framework becomes essential for robust theoretical analysis and a deeper understanding of the convergence properties of algorithms dealing with perturbed or approximated gradients.
USAM Analysis#
An analysis of Unnormalized Sharpness-Aware Minimization (USAM) would delve into its convergence properties, comparing it to the normalized SAM. Key aspects would include examining the impact of removing the normalization factor on the algorithm’s stability and efficiency, particularly concerning its ability to escape sharp minima. A crucial point would be to analyze the trade-off between generalization performance and convergence speed. The analysis should investigate how the absence of normalization affects the method’s theoretical guarantees and its practical performance on various datasets and network architectures. The investigation of different step size rules and perturbation radius strategies is vital in understanding the method’s behavior under different conditions. Finally, a comparison of USAM’s convergence rates with those of SAM and other optimization algorithms would provide valuable insights into its overall effectiveness and potential areas of improvement.
Stepsize Strategies#
Stepsize selection is crucial for optimization algorithms, and the choice significantly impacts convergence speed and stability. Constant stepsizes, while simple, often fail to achieve optimal performance, particularly in non-convex landscapes. Diminishing stepsizes, on the other hand, guarantee convergence under certain conditions, but may lead to slow convergence in practice. The paper explores these issues, analyzing the convergence behavior of the algorithm under various stepsize schedules. This investigation reveals the trade-off between the simplicity of constant stepsizes and the theoretical guarantees of diminishing stepsizes. The authors likely propose or evaluate adaptive stepsize schemes, such as those based on line search or curvature information, to balance these considerations. Analyzing the effectiveness of these strategies across various problem settings and comparing their performance against constant and diminishing stepsize methods forms a critical part of the study. The results likely highlight the superiority of adaptive schemes in terms of both efficiency and robustness. The implications of this research underscore the importance of a thoughtful stepsize selection process for effective optimization, emphasizing that a one-size-fits-all approach is rarely optimal.
Future Research#
The paper’s core contribution is a rigorous convergence analysis of Sharpness-Aware Minimization (SAM) and its variants. Future research could explore extending this analysis to stochastic settings, which are more common in practice. Investigating the impact of momentum on convergence would also be valuable. The current analysis focuses on deterministic settings, so incorporating noise and stochasticity into the model would make it more practical. Furthermore, while the paper touches on applications, more comprehensive empirical studies on a broader range of tasks and datasets could further illuminate SAM’s efficacy. Finally, exploring adaptive perturbation radius strategies could improve performance beyond constant or diminishing step-size schemes. In addition, examining SAM within the context of other optimization algorithms, such as those using second-order information, may reveal new synergies and enhance convergence performance.
More visual insights#
More on figures

This figure displays the training loss curves for four different deep neural network models (ResNet18, ResNet34, WideResNet28-10) trained on the CIFAR-10 and CIFAR-100 datasets using SAM with various stepsize strategies. The x-axis represents the training epoch, and the y-axis represents the training loss. Each line corresponds to a different stepsize schedule: ‘Constant’, ‘Diminish 1’, ‘Diminish 2’, and ‘Diminish 3’. The plot visualizes how different stepsize strategies affect the convergence behavior of the training loss during the training process of deep neural networks.
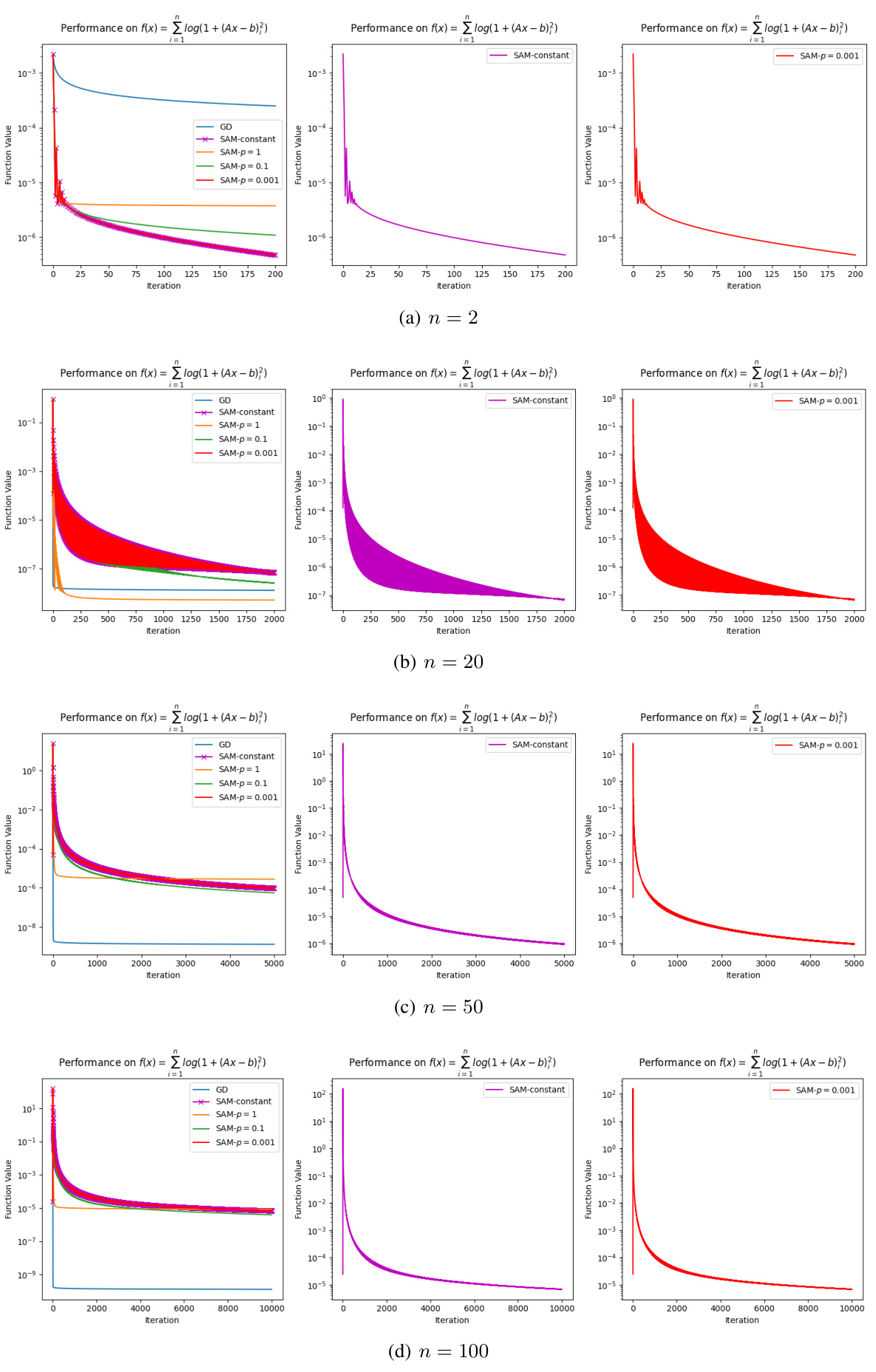
This figure presents the results of numerical experiments comparing the performance of SAM with a constant perturbation radius and SAM with an almost constant perturbation radius. The experiments were conducted on the function f(x) = ∑i=1log(1 + (Ax – b)²) with different dimensions (n = 2, 20, 50, 100). The results show that SAM with an almost constant perturbation radius (pk = C/kp) performs similarly to SAM with a constant perturbation radius (p = C), supporting the claim in Remark 3.6 that these two approaches have similar convergence behavior. The plots show the function value over iterations for both approaches, along with Gradient Descent (GD) as a comparison.
More on tables

This table summarizes the convergence properties of the Sharpness-Aware Minimization (SAM) algorithm for convex functions, as proven in Theorem 3.2 of the paper. It shows the relationship between different classes of convex functions (general setting, bounded minimizer set, unique minimizer) and the resulting convergence properties of the SAM algorithm. The convergence properties include the limit inferior of the gradient norm, the existence of a stationary accumulation point, and the convergence of the iterates themselves.

This table summarizes the convergence properties of SAM and its normalized variants, as well as USAM and its unnormalized variants. It shows the convergence results (e.g., limit of the gradient norm, convergence of function values, convergence of iterates) under different assumptions on the function (general setting, KL property, Lipschitz gradient). The table highlights the different convergence results achieved for convex vs nonconvex functions and also highlights the specific theorems/corollaries which provide the proofs of each result.

This table presents five fundamental convergence properties frequently analyzed in smooth optimization methods. These properties describe the convergence behavior of the iterates (xk), gradients (∇f(xk)), and function values (f(xk)) as the algorithm progresses. Property (1) states that the gradient norms approach zero in the limit inferior sense. Property (2) indicates that every accumulation point is a stationary point. Property (3) signifies that the gradient norms converge to zero. Property (4) states that the function values converge to the optimal value at some stationary point. Property (5) shows that the iterates converge to a stationary point. The relationships between these properties are also illustrated.

This table presents the convergence properties of the Sharpness-Aware Minimization (SAM) algorithm for convex functions, as proven in Theorem 3.2 of the paper. It shows the convergence results under different assumptions about the function’s minimizer set. Specifically, it shows what can be concluded about the limit inferior of the gradient norm, whether a stationary accumulation point exists, and whether the sequence of iterates converges to a solution. The conditions under which these conclusions are valid are that the gradient is Lipschitz continuous and that either there is a bounded minimizer set or a unique minimizer.
This table summarizes the convergence properties of the Sharpness-Aware Minimization (SAM) algorithm for convex functions, as proven in Theorem 3.2 of the paper. It shows the relationship between different convergence properties under different assumptions about the function’s minimizer set (general setting, bounded minimizer set, unique minimizer). The table shows that under increasingly restrictive assumptions on the minimizer set, increasingly stronger convergence properties can be guaranteed for SAM.

This table summarizes the convergence properties of the Sharpness-Aware Minimization (SAM) algorithm for convex functions, as proven in Theorem 3.2 of the paper. It shows the relationship between different convergence properties under varying conditions. For instance, it shows that if the function has a bounded minimizer set, SAM achieves a stationary accumulation point. If there is a unique minimizer, the sequence of iterates converges to that solution.

This table summarizes the fundamental convergence properties that are typically studied for smooth optimization methods. These properties include the convergence of the gradient norms to zero, the existence of stationary accumulation points, the convergence of function values to the optimal value, and the convergence of iterates to an optimal solution. The table provides a concise overview of these properties and their relationships, which serves as a benchmark for comparing the convergence behavior of the Sharpness-Aware Minimization (SAM) method against other optimization methods.
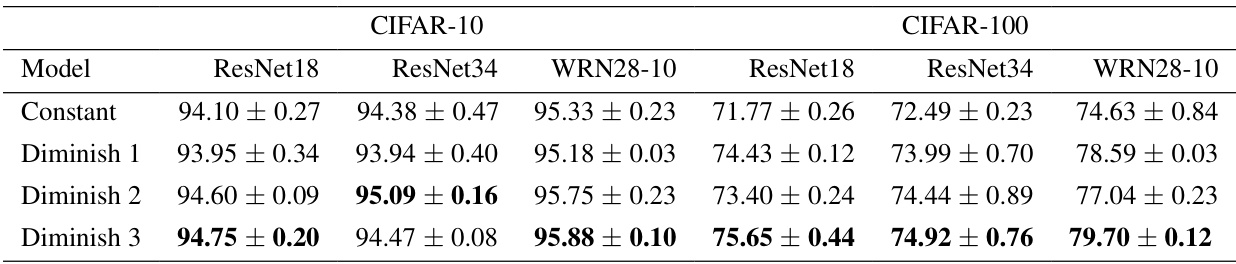
This table presents the test accuracy results on CIFAR-10 and CIFAR-100 datasets for different deep learning models (ResNet18, ResNet34, and WideResNet28-10) and different stepsize strategies (constant and diminishing). The results show the mean accuracy and the 95% confidence interval across three independent runs for each model and stepsize combination. It allows for a comparison of the performance of SAM with different stepsize schemes on popular image classification tasks.

This table summarizes the convergence properties of the Sharpness-Aware Minimization (SAM) algorithm for convex functions, as established in Theorem 3.2 of the paper. It shows the relationship between different convergence properties, such as the limit inferior of the gradient norm going to zero, the existence of a stationary accumulation point, and the convergence of the iterates to a minimizer under different assumptions on the minimizer set (general, bounded, or unique).
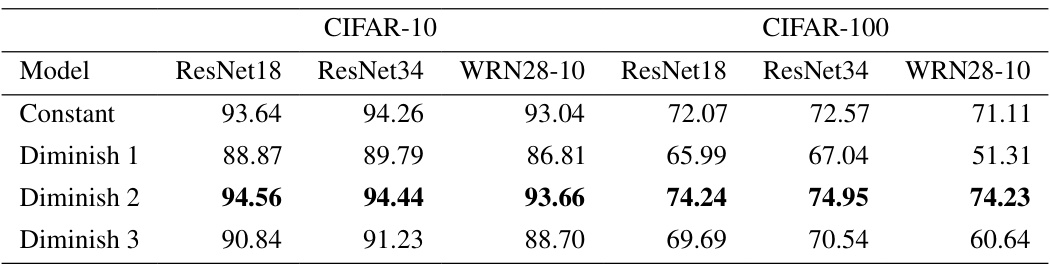
This table presents the test accuracy results for different deep neural network models trained on CIFAR-10 and CIFAR-100 datasets using SAM with various stepsize strategies. The models include ResNet18, ResNet34, and WideResNet28-10. The stepsize strategies are ‘Constant’, ‘Diminish 1’, ‘Diminish 2’, and ‘Diminish 3’, representing different diminishing stepsize schemes. The table shows the mean test accuracy and its 95% confidence interval across three independent runs for each model and stepsize strategy on each dataset. The highest accuracy for each model and dataset is highlighted in bold, allowing comparison of the performance across the different stepsize approaches.
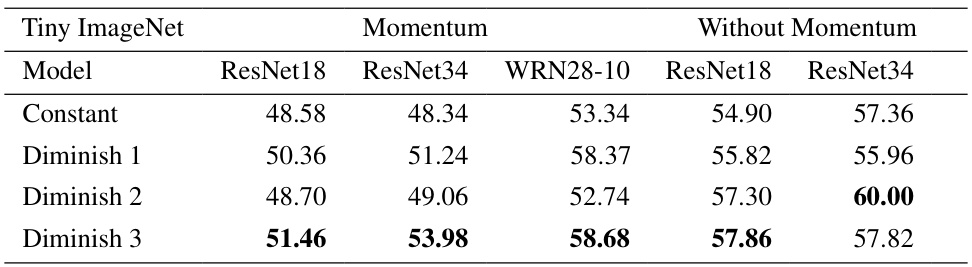
This table presents the test accuracy results on the Tiny ImageNet dataset using different stepsize strategies for the SAM optimization algorithm. It compares the performance of SAM with and without momentum. The results show the test accuracy for four different deep neural network models (ResNet18, ResNet34, WideResNet28-10) under four different stepsize schemes (Constant, Diminish 1, Diminish 2, Diminish 3). The highest accuracy for each model and stepsize scheme is bolded.
Full paper#



















