Who’s Gaming the System? A Causally-Motivated Approach for Detecting Strategic Adaptation

PXGY9Fz8vC

Trenton Chang et el.

TL;DR
#

Many machine learning models inform decisions impacting interacting agents, who might strategically manipulate inputs for better outcomes. Identifying such agents is difficult without knowing their utility functions. Existing methods struggle with this challenge, particularly when costs for manipulation vary across agents. This makes detecting strategic behavior such as upcoding (fraudulent insurance claims) challenging.

This research presents a novel framework to tackle this problem by introducing a ‘gaming deterrence parameter’, quantifying an agent’s gaming willingness. It shows that this parameter is partially identifiable. However, it proves that ranking agents based on the parameter is identifiable by recasting the problem as a causal effect estimation problem, where agents represent different treatments. The study validates this method using synthetic data and a real-world case study of diagnosis coding in the US healthcare system.

Key Takeaways
#

Why does it matter?
#

This paper is crucial for researchers working on strategic classification, anomaly detection, and causal inference due to its novel framework for detecting strategic adaptation in multi-agent settings. It bridges the gap between these fields, providing valuable tools and insights for identifying and mitigating gaming behavior in real-world applications.

Visual Insights
#

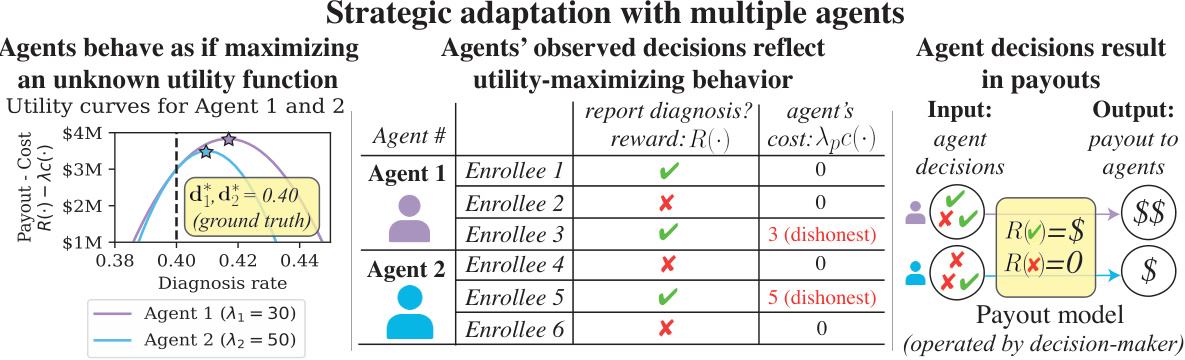
This figure illustrates the core concepts of the paper using a simplified example of two agents making decisions that affect their reward, influenced by a gaming deterrence parameter (λ). The left panel shows how the optimal diagnosis rate (the point where reward minus cost is maximized) varies based on the agent’s willingness to game (λ). The higher the λ, the less willing they are to game (thus, the diagnosis rate is closer to the ground truth). The center panel shows the observed diagnosis decision made by each agent, reflecting the utility maximization behavior. The right panel shows how the decision maker computes the payout based on the agents’ decisions.

This table shows the top five state-level healthcare system statistics that are most positively and negatively correlated with the state gaming rankings as predicted by the S+IPW model. The correlations are measured by Spearman rank correlation and p-values indicate the significance of those correlations against a null hypothesis of zero correlation. Abbreviations include OP PT/SP (Outpatient physical therapy and speech pathology) and SNF (skilled nursing facility).

In-depth insights
#

Gaming Detection
#

The paper explores gaming detection in machine learning models, focusing on scenarios where agents strategically adapt their inputs to influence model outcomes. A key challenge is the identification of agents gaming most aggressively, which is difficult without knowledge of their utility functions. The proposed framework introduces a gaming deterrence parameter, which quantifies an agent’s willingness to game. The authors demonstrate that this parameter is partially identifiable, yet a ranking of all agents by their gaming propensities is achievable. This ranking is obtained by recasting the problem as a causal effect estimation problem, enabling identification of the “worst offenders.” Empirical evaluation in synthetic and real-world datasets (U.S. Medicare claims data) supports the effectiveness of this approach, highlighting its potential for detecting strategic behavior and informing targeted interventions.

Causal Inference
#

Causal inference, in the context of detecting strategic adaptation, offers a powerful framework for ranking agents based on their propensity to game a system. Traditional methods often fail to identify the “worst offenders” because they lack the ability to disentangle the effects of agents’ strategic actions from confounding variables. By framing the problem as a causal effect estimation problem, where agents represent different treatments and their actions are outcomes, identifiable rankings of agents based on a gaming parameter become possible, even when the utility function of agents remains unknown. This approach proves particularly robust because it sidesteps the need for strong assumptions about agents’ cost functions or their gaming behavior, and offers a more nuanced understanding of gaming than simply relying on anomaly detection or supervised learning.

Medicare Upcoding
#

Medicare upcoding, the fraudulent practice of assigning higher-level diagnosis codes to increase reimbursements, presents a significant challenge to the healthcare system. This practice inflates healthcare costs for taxpayers and insurance providers. The paper highlights the difficulty in detecting upcoding due to the lack of readily available ground truth labels and the complexity of establishing causality between provider actions and the resulting financial outcomes. The use of machine learning models to identify potential upcoding cases is explored, focusing on a causally-motivated approach that ranks healthcare providers based on their propensity to engage in upcoding. This causal inference approach offers an innovative solution to a persistent problem, but its effectiveness is dependent on the accuracy of assumptions and data quality, especially in handling confounding factors. The study’s findings emphasize the need for further research into causal inference techniques to refine upcoding detection. The approach, while promising, requires robust methods to account for the various incentives impacting provider behavior, making reliable quantification of gaming deterrence parameters a critical area for future improvements.

Limitations & Future
#

The research paper’s “Limitations & Future” section would critically examine the study’s inherent constraints, acknowledging the strong assumptions made about agent behavior (utility maximization) and the challenge of verifying causal effects without exhaustive ground truth data. It would discuss the limitations of focusing solely on ranking agents instead of precisely quantifying gaming propensity, and the impact of potential unmeasured confounding variables on the accuracy of causal effect estimations. Future research directions could involve exploring alternative methods for handling unknown costs of gaming, leveraging techniques that can handle multi-agent settings more effectively, and investigating how to relax restrictive assumptions such as perfect rationality or cost homogeneity. The section might also highlight the potential for extending the framework to include non-binary decisions, and the importance of addressing ethical implications, particularly the risk of reinforcing biases or power imbalances through the application of such a system. Finally, future work should explore the generalizability to settings with complex reward structures and differing agent capabilities.

Synthetic Data Study
#

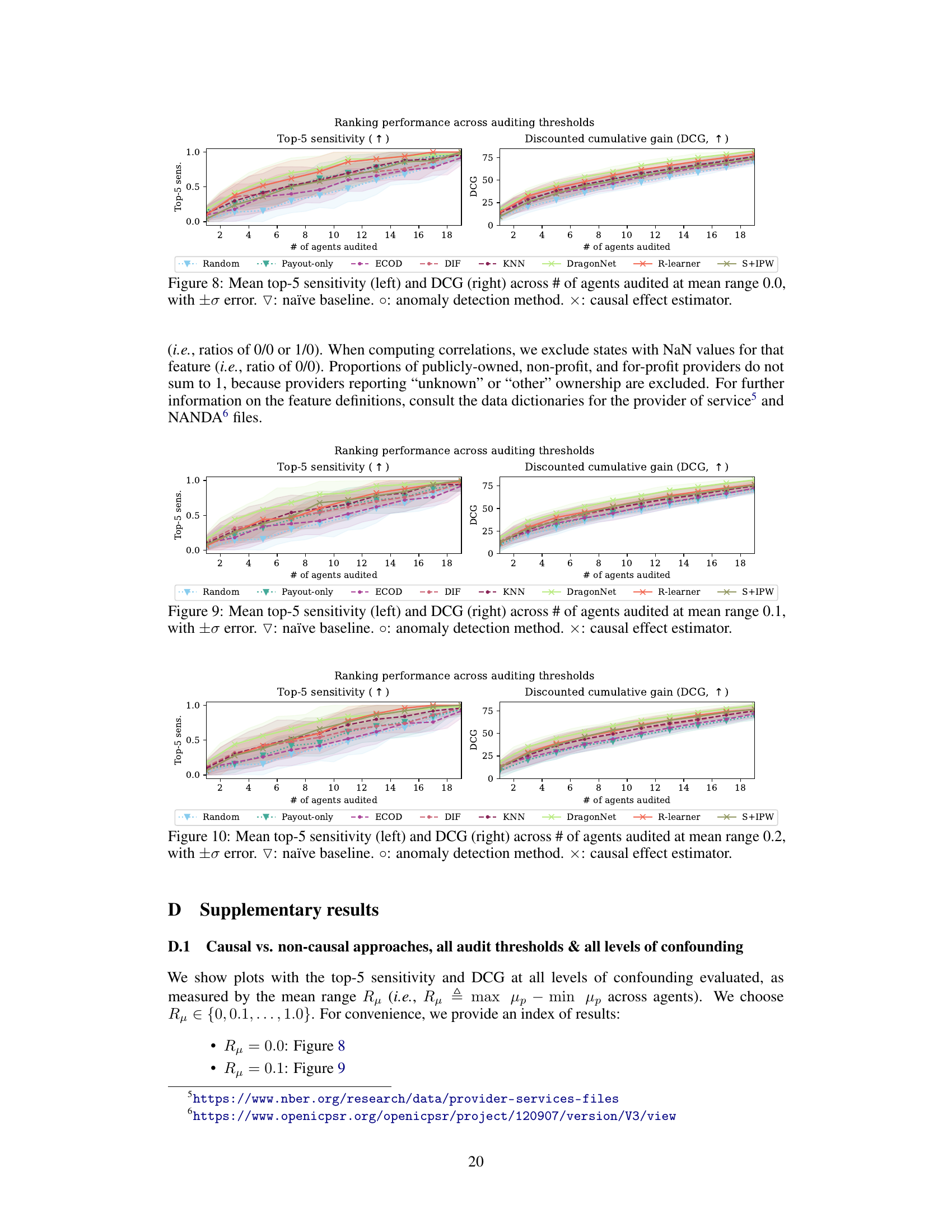
A synthetic data study in a research paper plays a crucial role in validating the proposed methodology. It allows researchers to control all aspects of data generation, including confounding factors and the ground truth of gaming behavior, thus enabling a rigorous evaluation of the model’s performance under various conditions. This controlled environment is essential for establishing causality and isolating the effects of the gaming deterrence parameter without the complexities and biases introduced by real-world data. By manipulating the parameters of data generation, researchers can test the model’s robustness and sensitivity across different scenarios. The results from the synthetic data study provide a foundation for the subsequent real-world analysis, showing that the causal inference model can effectively identify the agents most likely to engage in gaming behavior and produces results correlated with known drivers of gaming.

More visual insights
#

More on figures

This figure demonstrates a toy dataset and causal graph to visualize the concept of causal effect estimation in detecting gaming behavior. The left panel presents a toy dataset with observed factual outcomes (di(p), di(p’)) and missing counterfactual outcomes represented by question marks. The right panel illustrates a causal graph showing how confounders (xi), agent indicators (pi), and agent decisions (di) are related for causal effect estimation in identifying the agents who are gaming most aggressively.

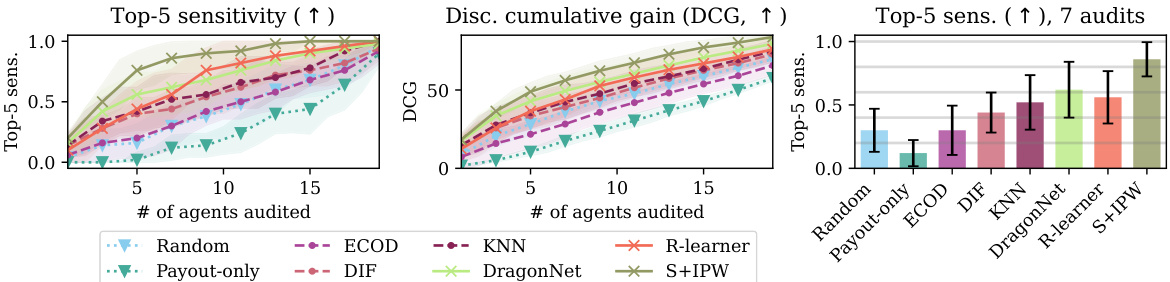
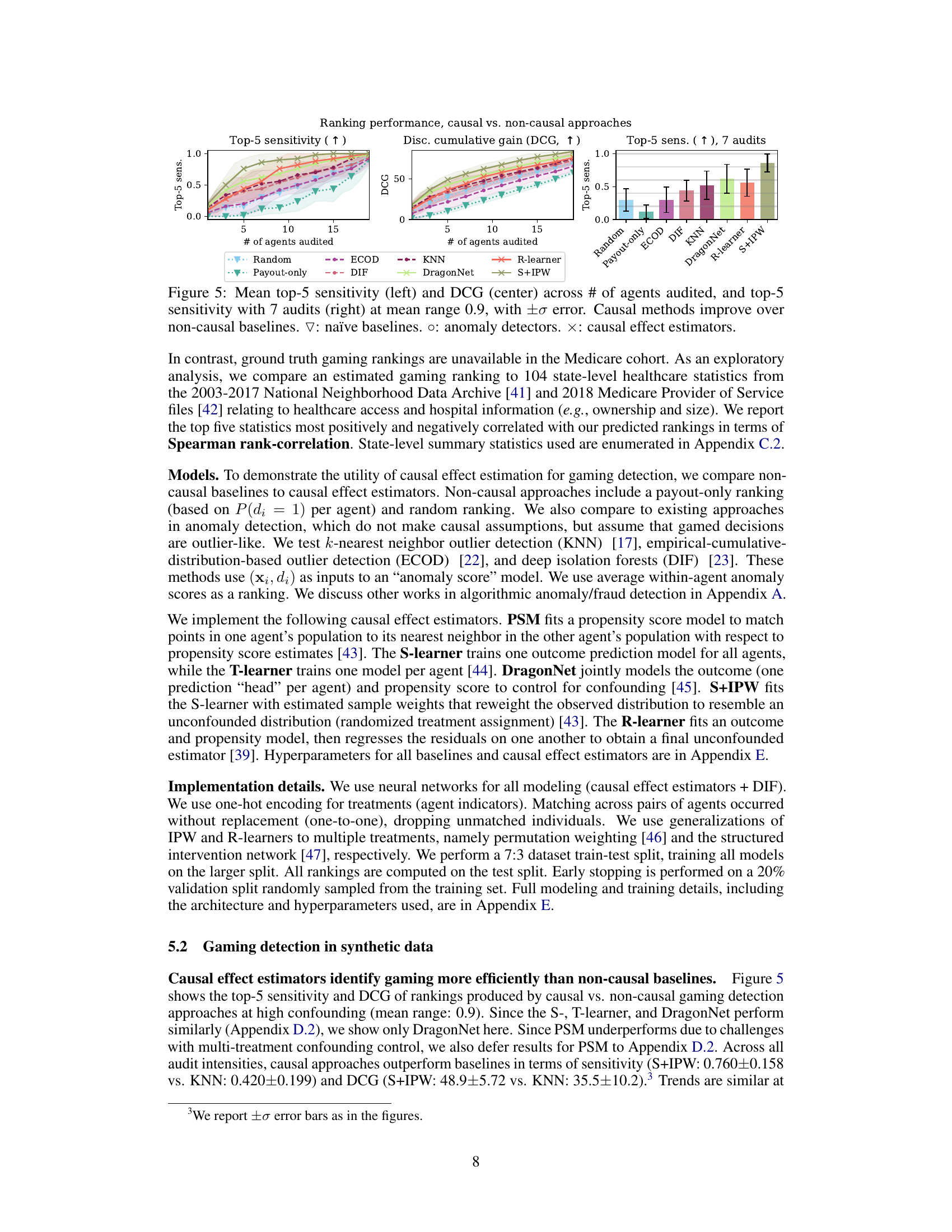
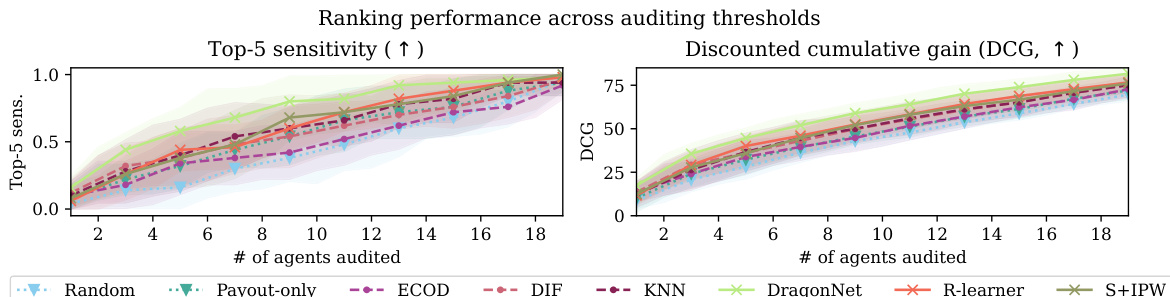
This figure compares the performance of causal and non-causal gaming detection approaches. It presents three subplots: Top-5 sensitivity versus the number of agents audited, Discounted Cumulative Gain (DCG) versus the number of agents audited, and Top-5 sensitivity with 7 audits. The results show that causal effect estimators consistently outperform other methods, including baselines (naive approaches and anomaly detection methods) in terms of both sensitivity and DCG, especially when the number of audits is limited.

This figure displays the performance of causal and non-causal methods for gaming detection in terms of top-5 sensitivity and discounted cumulative gain (DCG), varying the number of agents audited. The left and center panels show the overall performance, while the right panel focuses on the top-5 sensitivity when auditing only 7 agents. The results demonstrate that causal methods consistently outperform non-causal baselines, showcasing their efficiency in identifying gaming agents.

This figure compares the performance of causal and non-causal gaming detection methods using two metrics: top-5 sensitivity and discounted cumulative gain (DCG). The results are shown for different numbers of agents audited, with a specific focus on the top-5 sensitivity when auditing 7 agents. The chart visually demonstrates that causal methods consistently outperform non-causal approaches across various auditing thresholds. The different symbols represent different types of approaches, with triangles representing naive baselines, circles representing anomaly detection methods, and crosses representing causal effect estimators.

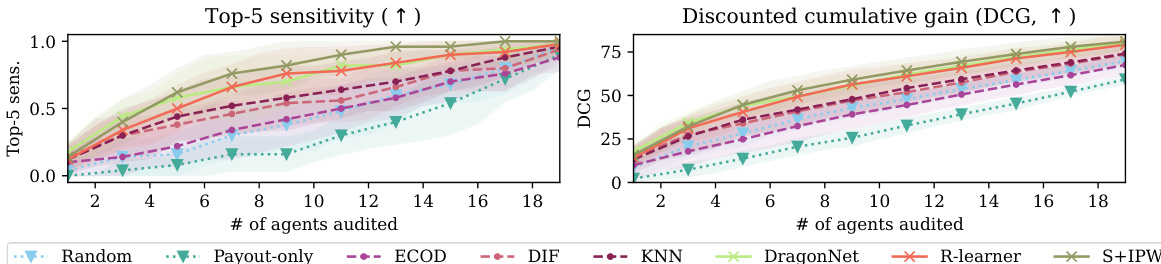
This figure compares the performance of causal and non-causal methods for detecting gaming agents in a synthetic dataset. The left panel shows the top-5 sensitivity (the percentage of the top 5 worst gaming agents correctly identified) across different numbers of agents audited, showing that causal methods are much better. The center panel shows the Discounted Cumulative Gain (DCG), a metric that rewards correctly identifying the worst offenders higher in the ranking. Again, causal methods perform better. The right panel is a zoomed-in view of the left panel, showing the top-5 sensitivity when only 7 agents are audited.

This figure compares the performance of causal and non-causal methods for gaming detection using two metrics: Top-5 sensitivity and Discounted Cumulative Gain (DCG). The results are shown for different numbers of agents audited and demonstrate the superiority of causal approaches in identifying the worst offenders. The plot shows that causal methods achieve significantly higher values for both sensitivity and DCG.

This figure compares the performance of causal and non-causal gaming detection methods in terms of top-5 sensitivity and discounted cumulative gain (DCG) across different numbers of audited agents. The causal methods consistently outperform the non-causal baselines, demonstrating their effectiveness in identifying the worst gaming offenders.

This figure compares the performance of causal and non-causal gaming detection methods. It shows the top-5 sensitivity (the percentage of the top 5 worst offenders correctly identified) and the discounted cumulative gain (DCG, a measure of ranking quality) across different numbers of agents audited. The results indicate that causal methods significantly outperform non-causal methods (naïve baselines and anomaly detection methods) in identifying the worst offenders.

This figure compares the performance of causal and non-causal methods for gaming detection in a synthetic dataset. The top-5 sensitivity shows the percentage of the top 5 worst offenders correctly identified by each method for a given number of audits. The discounted cumulative gain (DCG) is a metric that assesses the ranking quality of each method, giving higher weights to correctly identifying the worst offenders at the top of the ranking. The figure demonstrates that causal methods significantly outperform non-causal methods in terms of both top-5 sensitivity and DCG, especially when considering a limited number of audits. The findings suggest that causal effect estimation is more efficient for identifying gaming agents.

This figure compares the performance of causal and non-causal methods for gaming detection in a synthetic dataset with a high level of confounding (mean range 0.9). The left panel shows top-5 sensitivity, indicating the percentage of the top 5 worst offenders correctly identified by each method at different numbers of audits. The center panel displays the Discounted Cumulative Gain (DCG), a metric that weighs the accuracy of higher-ranked agents more heavily. The right panel shows the top-5 sensitivity specifically at 7 audits. The results demonstrate that causal effect estimators (marked with ‘x’) consistently outperform non-causal baselines (marked with ‘▽’ and ‘o’) in both sensitivity and DCG, indicating their superior ability to identify the most severe gaming cases with fewer audits.

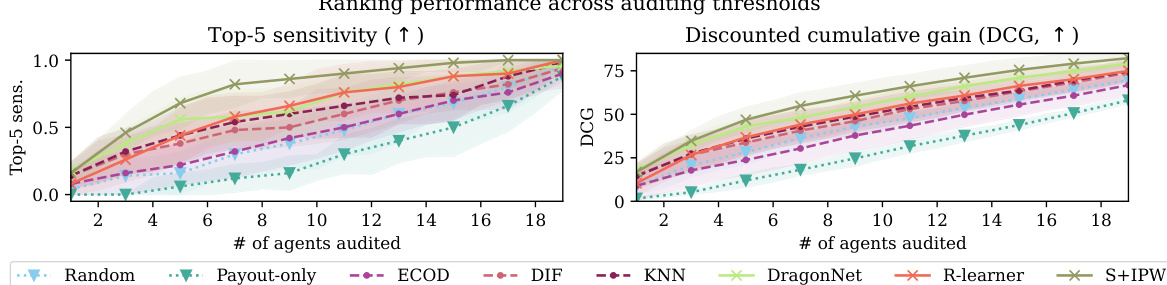
This figure compares the performance of causal and non-causal methods for gaming detection across different numbers of agents audited. The left panel shows the top-5 sensitivity, which measures the percentage of the top 5 worst offenders correctly identified among the top k predicted offenders. The center panel shows the discounted cumulative gain (DCG), which measures the ranking quality based on the predicted and actual ranks of the worst offenders. The right panel focuses specifically on the top-5 sensitivity with 7 audits. The results indicate that causal methods consistently outperform non-causal methods in both ranking quality and efficiency of detecting the worst offenders.

This figure compares the performance of causal and non-causal methods for gaming detection across different numbers of agents audited. The top-5 sensitivity measures the percentage of the top 5 worst offenders correctly identified among the top k agents. The DCG (Discounted Cumulative Gain) is another metric that weighs the rank of correctly identified offenders. The plot shows that causal effect estimators (marked with an x) outperform both naive baselines (▽) and anomaly detection methods (o) in terms of both top-5 sensitivity and DCG. A separate plot on the right also shows that causal methods maintain their superiority even when only 7 agents are audited.

This figure compares the performance of causal and non-causal methods for gaming detection across different numbers of agents audited. The results show that causal methods (represented by ‘x’) outperform non-causal methods (represented by ‘▽’ and ‘o’) in terms of both top-5 sensitivity (the percentage of the top 5 worst offenders correctly identified) and DCG (discounted cumulative gain, a measure of ranking quality). The right panel shows the top-5 sensitivity when only 7 agents are audited.

This figure compares the performance of causal and non-causal methods in detecting gaming agents. The x-axis represents the number of agents audited, while the y-axis shows the top-5 sensitivity (proportion of top 5 worst offenders correctly identified) and DCG (Discounted Cumulative Gain, measuring ranking quality). The figure demonstrates that causal effect estimators outperform both non-causal baselines (random and payout-only) and anomaly detection methods.

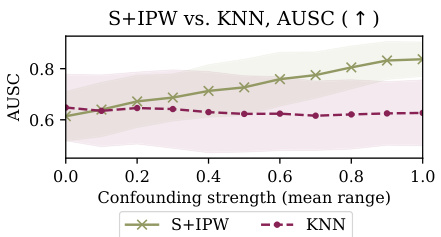
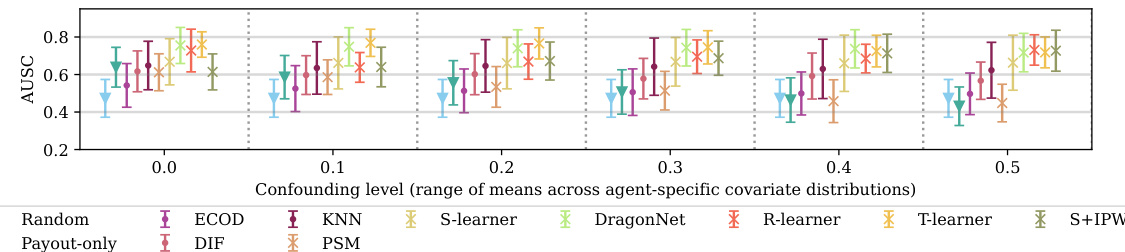
This figure shows the area under the sensitivity curve (AUSC) for different gaming detection methods across various levels of confounding. It compares the performance of causal and non-causal methods, highlighting how causal methods generally maintain a higher AUSC than baselines across different levels of confounding, while anomaly detection methods exhibit performance close to random regardless of the confounding level. The figure also illustrates the degradation of the payout-only method’s performance as confounding increases.

This figure compares the performance of causal and non-causal methods for detecting gaming agents. The left panel shows the top-5 sensitivity, indicating the percentage of the top 5 worst gaming agents correctly identified. The center panel displays the Discounted Cumulative Gain (DCG), measuring the ranking quality. The right panel focuses on the top-5 sensitivity when only auditing 7 agents. Across all metrics, causal methods consistently outperform non-causal approaches (naive baselines, anomaly detection, and payout-only).

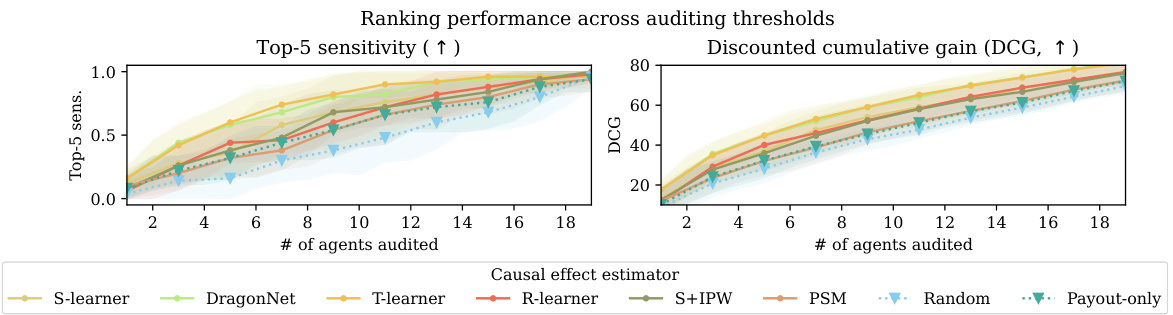
This figure compares the performance of causal effect estimators and non-causal baselines for gaming detection across different numbers of agents audited. The left panel displays top-5 sensitivity, showing the percentage of times the top 5 true worst offenders were caught within the top k predicted offenders. The center panel shows the discounted cumulative gain (DCG), a metric evaluating the ranking’s overall effectiveness in identifying the worst offenders. The right panel shows the same top-5 sensitivity measure but focuses specifically on auditing 7 agents. The results indicate that causal methods outperform non-causal approaches in gaming detection, especially when considering a limited number of audits.

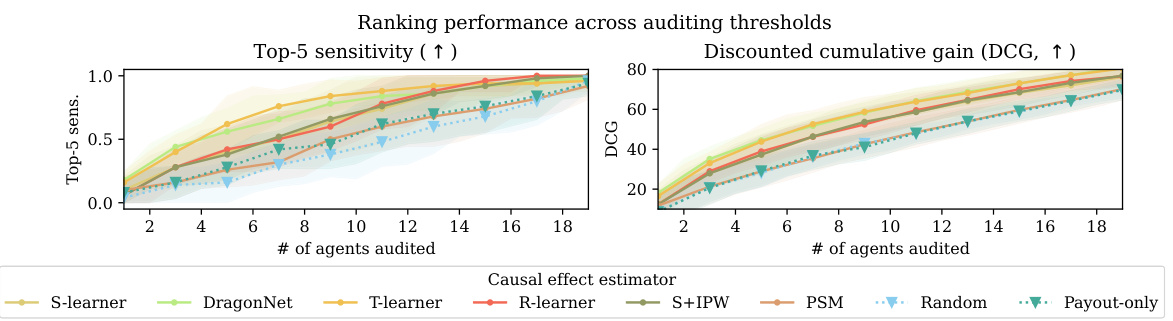
This figure compares the performance of causal and non-causal gaming detection approaches in terms of top-5 sensitivity and discounted cumulative gain (DCG) across different numbers of agents audited. The results demonstrate that causal methods outperform non-causal baselines, especially in terms of identifying the top 5 worst offenders.

This figure displays the performance of causal and non-causal gaming detection methods across different numbers of agents audited. The performance is measured using two metrics: top-5 sensitivity and discounted cumulative gain (DCG). The left panel shows the top-5 sensitivity, which represents the percentage of the top five worst gaming agents that are correctly identified among the top k agents audited. The center panel shows the DCG, which weighs the importance of correctly ranking the worst offenders higher. The right panel shows the top-5 sensitivity specifically when only 7 agents are audited. The results indicate that causal methods consistently outperform non-causal baselines in identifying and ranking the worst gaming agents.

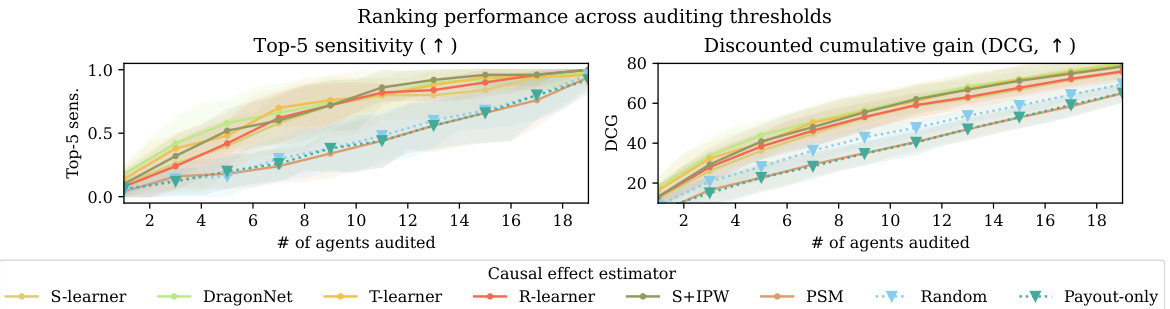
This figure compares the performance of causal and non-causal gaming detection methods across different numbers of agents audited. The left panel shows the top-5 sensitivity, measuring the percentage of the top 5 worst offenders correctly identified. The center panel shows the discounted cumulative gain (DCG), a metric that rewards higher-ranked worst offenders. The right panel shows a zoomed-in view of the top-5 sensitivity when only 7 agents are audited. The results demonstrate that causal effect estimation methods outperform non-causal baselines, particularly in terms of identifying the worst offenders using fewer audits.

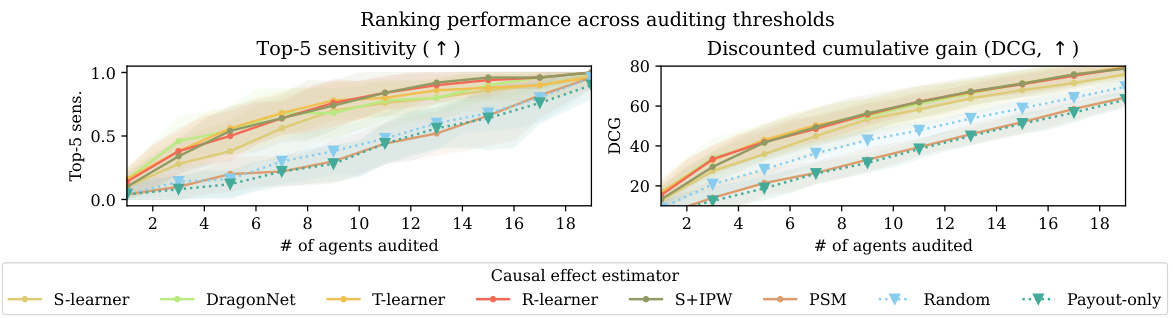
This figure compares the performance of causal and non-causal methods for gaming detection in a synthetic dataset with high confounding (mean range of 0.9). The left panel shows the top-5 sensitivity, which represents the percentage of the top 5 worst offenders correctly identified by the method. The center panel shows the discounted cumulative gain (DCG), a metric that considers the ranking of the agents. The right panel displays the top-5 sensitivity when only 7 agents are audited. The results indicate that causal methods (represented by ×) generally outperform non-causal baselines (▽ and 0), especially in terms of identifying the worst offenders.

This figure compares the performance of causal and non-causal methods for gaming detection in terms of top-5 sensitivity and discounted cumulative gain (DCG) across different numbers of agents audited. The left panel shows top-5 sensitivity, which measures the percentage of the top 5 worst offenders correctly identified. The center panel shows DCG, which measures the ranking quality of top offenders. The right panel displays top-5 sensitivity when only 7 agents are audited. The results indicate that causal methods (represented by ‘x’) outperform non-causal baselines (represented by ‘▽’ and ‘o’) in both metrics, highlighting their effectiveness in detecting gaming behavior.

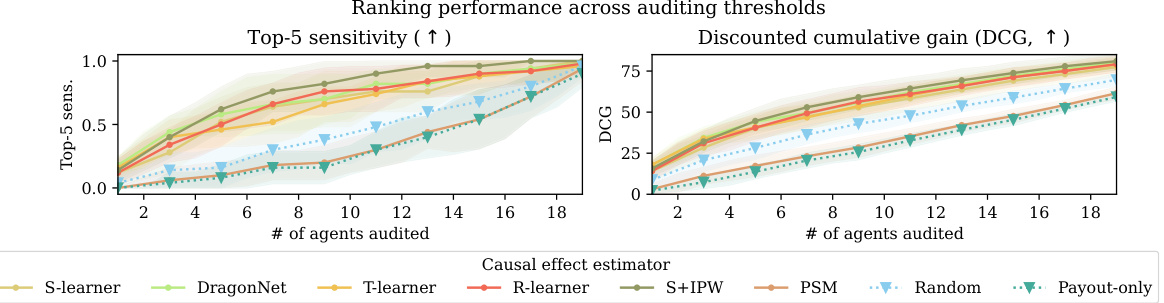
This figure displays the results of comparing causal and non-causal methods for gaming detection. The left panel shows the top-5 sensitivity, measuring the percentage of the top 5 worst offenders correctly identified among the top k agents audited. The center panel presents the Discounted Cumulative Gain (DCG), which weights the correctly identified worst offenders higher. Both metrics are plotted against the number of agents audited. The right panel shows top-5 sensitivity when auditing only 7 agents. The results indicate that causal effect estimation methods outperform both naive and anomaly detection baselines across different metrics and audit levels. The plot uses symbols to distinguish between different categories of methods (naive, anomaly detection, and causal).

This figure compares the performance of causal and non-causal methods for gaming detection in terms of top-5 sensitivity and discounted cumulative gain (DCG). The x-axis represents the number of agents audited, and the y-axis shows the performance metrics. The results demonstrate that causal methods outperform non-causal baselines, particularly as the number of audited agents increases. Three different performance metrics are presented, with error bars for each. Different symbols represent different gaming detection methods.

This figure compares the performance of causal and non-causal methods for gaming detection across different numbers of agents audited. Top-5 sensitivity measures the percentage of the top 5 worst offenders correctly identified among the top k agents. DCG (Discounted Cumulative Gain) weights higher-ranked offenders more heavily than lower-ranked offenders. The results show causal methods generally outperform non-causal baselines in terms of both metrics. The right panel shows the top-5 sensitivity when auditing only 7 agents.

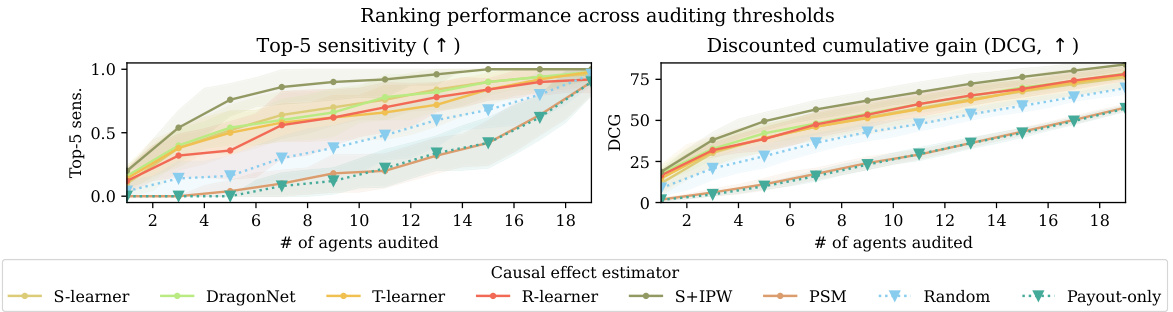
This figure compares the performance of causal and non-causal gaming detection methods across different auditing thresholds. The top-5 sensitivity measures the percentage of the five worst gaming agents correctly identified within the top-k ranked agents. Discounted Cumulative Gain (DCG) provides a weighted ranking score, giving higher weights to correctly ranking the worst agents higher. The figure shows that causal methods (marked with ×) consistently outperform non-causal baselines (▽ and ∘) across various auditing numbers, indicating their superior ability to effectively identify and rank the worst gaming agents. The right panel shows the top-5 sensitivity when 7 agents are audited.