On the Computational Complexity of Private High-dimensional Model Selection

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on high-dimensional sparse regression and differential privacy. It bridges the gap between theoretical efficiency and practical applicability of private model selection, opening new avenues for privacy-preserving machine learning in sensitive data applications. The polynomial-time algorithm and the rigorous theoretical guarantees are significant advancements in the field.

Visual Insights

#

This figure visualizes the performance of the Metropolis-Hastings algorithm across various privacy budgets (ε) and regularization parameters (K). Each subplot represents a different combination of ε and K, showing the evolution of the model’s F1 score (a metric of model accuracy) and Ry (a measure of the model’s goodness of fit). The red dashed line indicates the F1 score of the non-private best subset selection, which serves as a baseline for comparison. The gray shaded region represents the interquartile range (IQR) across ten independent MCMC runs, highlighting the variability in the algorithm’s performance. This visualization helps to understand how the algorithm’s performance and stability are influenced by varying privacy and regularization levels under a strong signal.

This table compares different differentially private (DP) model selection methods from prior works and the proposed method in the paper. It shows the minimum signal strength (β_min) condition required for each method, whether the failure probability approaches 0, and the runtime complexity. The proposed method, using an approximate exponential mechanism via Markov Chain Monte Carlo (MCMC), offers improved runtime and similar utility guarantees compared to existing approaches.

In-depth insights

#

Private Model Selection

#

Private model selection, a crucial aspect of privacy-preserving machine learning, focuses on selecting the optimal model while adhering to strict privacy constraints. The core challenge lies in balancing the need for accurate model selection with the requirement of safeguarding sensitive data. Differentially private mechanisms, such as the exponential mechanism, offer a robust approach to achieving privacy. However, these methods often come with a trade-off: the more stringent the privacy requirements, the greater the loss in statistical utility, potentially leading to suboptimal model selection. Computational efficiency is another significant hurdle, especially in high-dimensional settings, where the search space for the optimal model grows exponentially. The development of efficient algorithms, such as the Metropolis-Hastings Markov Chain Monte Carlo method, that efficiently explores the model space while satisfying differential privacy constraints is therefore essential. Future research should focus on bridging the gap between strong privacy guarantees and high statistical utility, as well as improving the scalability of private model selection algorithms to handle increasingly large and complex datasets.

MCMC Algorithm

#

The effectiveness of the proposed differentially private best subset selection (BSS) method hinges on an efficient Markov Chain Monte Carlo (MCMC) algorithm. This MCMC algorithm is crucial for sampling from a complex, high-dimensional probability distribution that arises from the exponential mechanism used to ensure differential privacy. The algorithm’s efficiency is key, as naive approaches would be computationally intractable. The authors demonstrate that their MCMC algorithm exhibits polynomial mixing time under certain regularity conditions, meaning it converges to its stationary distribution relatively quickly. This ensures that the generated samples accurately reflect the target distribution, preserving both privacy and utility. The theoretical analysis of the mixing time is a significant contribution, providing a formal guarantee of computational feasibility. The chosen Metropolis-Hastings approach, coupled with a double-swap update scheme, facilitates efficient exploration of the model space. Empirical experiments showcase the algorithm’s ability to rapidly identify active features under realistic privacy constraints, supporting the theoretical findings.

Utility and Privacy

#

Balancing utility and privacy in data analysis presents a fundamental challenge. Strong privacy guarantees, often achieved through noise addition or other randomization techniques, can compromise the accuracy and utility of the results. Conversely, prioritizing utility by minimizing privacy-preserving mechanisms may expose sensitive information. The optimal balance depends on the specific application and the sensitivity of the data. Quantifying this trade-off requires careful consideration of the privacy budget (e.g., epsilon and delta in differential privacy) and the utility metric (e.g., accuracy, F1-score, or model recovery). There’s an ongoing research effort to develop mechanisms that offer both strong privacy and high utility, including advanced techniques like the exponential mechanism and techniques based on Markov Chain Monte Carlo methods, which improve computational efficiency in high-dimensional settings. However, achieving optimal utility under strict privacy constraints often requires stronger assumptions on the data generating process or limitations on the model’s complexity. Future research may explore further refinements of these methods and the development of new privacy-preserving techniques tailored to specific data types and applications.

Computational Cost

#

Analyzing the computational cost of differentially private high-dimensional model selection reveals crucial trade-offs. The exponential mechanism, while offering strong privacy guarantees, suffers from an exponential runtime due to its exhaustive search. This motivates the use of a Metropolis-Hastings Markov Chain Monte Carlo (MCMC) algorithm, which trades off some statistical utility for significant computational efficiency. The paper demonstrates polynomial mixing time under certain regularity conditions, implying that the MCMC method achieves a computationally feasible solution. However, the mixing time’s dependence on problem parameters (n, p, s) highlights the computational challenge in high-dimensional settings. The success of the MCMC approach hinges on assumptions about model correlation and signal strength, underscoring a potential bottleneck in practical applications. Future research directions should investigate alternative approaches and explore ways to reduce the dependency on strong assumptions to make the methods more robust and applicable to a wider range of scenarios.

Future Directions

#

The research paper’s ‘Future Directions’ section would ideally explore avenues for enhancing the proposed differentially private best subset selection (DP-BSS) method. Improving computational efficiency is crucial, perhaps through exploring advanced MCMC techniques or alternative optimization strategies beyond Metropolis-Hastings. Relaxing the strong assumptions on the design matrix and signal strength would broaden the applicability of DP-BSS to more realistic scenarios. Furthermore, the paper could delve into theoretical analysis of the algorithm’s robustness under noisy data or model misspecification. Finally, developing a comprehensive framework that extends beyond linear models and addresses a wider range of model selection problems in a differentially private manner would be significant. Investigating the practical implications of the DP-BSS method across diverse sensitive data domains, such as genomics and healthcare, would also be a crucial next step.

More visual insights

#

More on figures

This figure displays the results of the Metropolis-Hastings random walk algorithm under different privacy budgets (ε) and l1 regularization parameters (K). It focuses on the ‘strong signal’ scenario. Each subplot shows the evolution of the F1 score and Ry (a measure of model quality) over iterations of the algorithm. Different colors represent different chains, and the red line indicates the F1 score of the non-private BSS estimator. The figure helps to visualize the convergence of the algorithm and its performance under various privacy constraints and regularization levels.

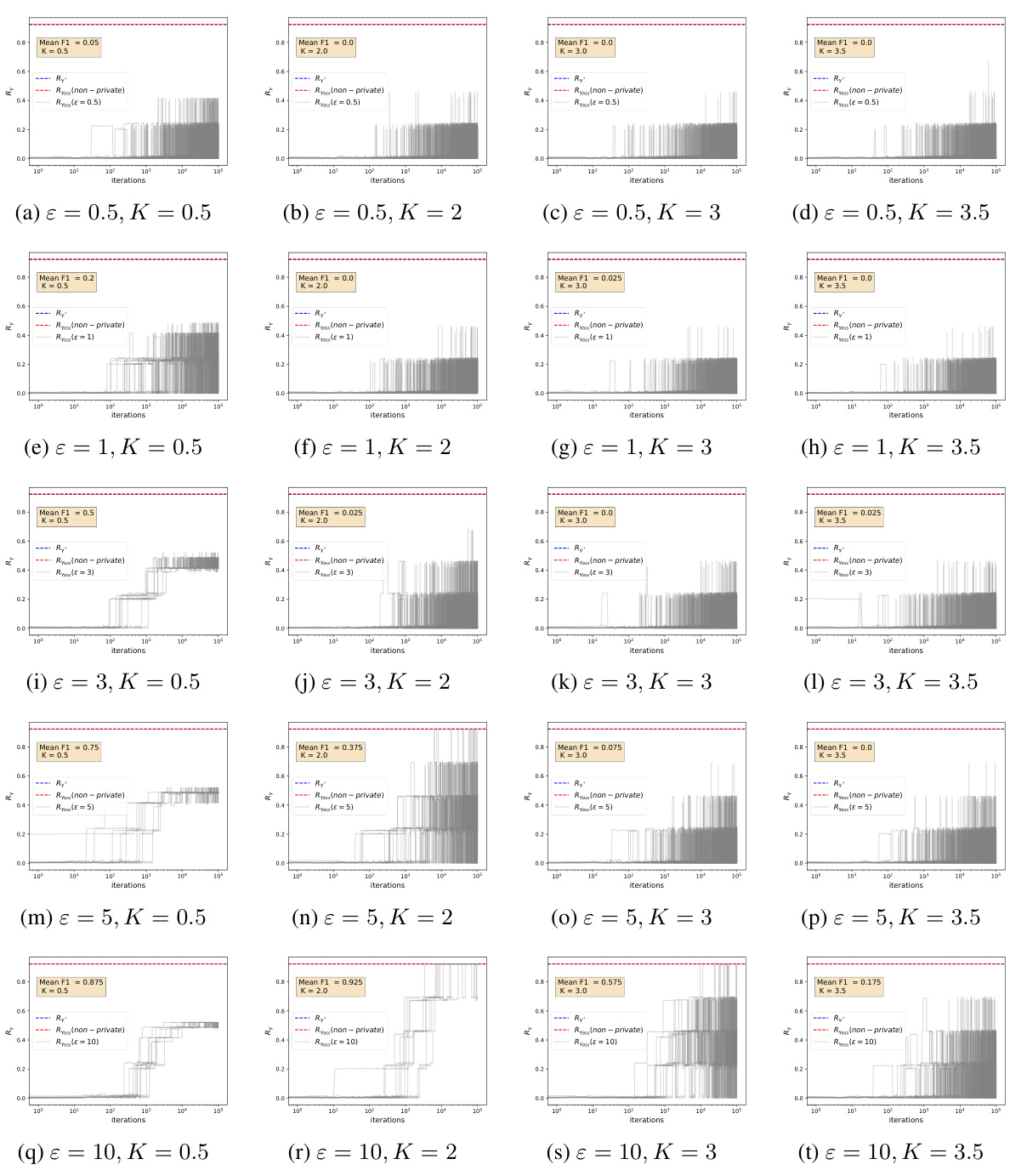
This figure shows the results of the Metropolis-Hastings algorithm for different privacy budgets (ε) and l₁ regularization parameters (K). Each subplot represents a different combination of ε and K, showing how the algorithm’s performance varies across different privacy levels and regularization strengths. The algorithm’s performance is evaluated by calculating the mean F1-score and tracking Ry which is proportional to the log-likelihood of the model, and this value increases as the chain progresses. The red horizontal line indicates the Ry value for the non-private BSS model; the gray area denotes the iterations of the Markov chain. The strong signal case has been shown here. The algorithm shows good performance for larger values of ε (lower privacy) and appropriately chosen K.

This figure displays the results of the Metropolis-Hastings random walk algorithm under various privacy budgets (ε) and l1 regularization parameters (K). The strong signal case is shown, where the signal strength is relatively high. Each subplot represents a different combination of ε and K, showing the F1 score (a measure of model accuracy) and Ry (a measure of model fit) over iterations of the algorithm. The red dashed line represents the F1 score of non-private BSS, serving as a baseline for comparison. This figure helps to visualize how the algorithm’s performance changes under differing levels of privacy and regularization.

Full paper

#