↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Learning sparse functions efficiently using gradient-based methods is a significant challenge in machine learning. Existing theoretical frameworks, such as Statistical Queries (SQ), often fail to capture the nuances of gradient-based optimization. This paper tackles this problem by introducing a new query model called Differentiable Learning Queries (DLQ), which accurately reflects gradient computations. The study focuses on the query complexity of DLQ for learning the support of a sparse function, revealing how this complexity is tightly linked to the choice of loss function.
The researchers demonstrate that the complexity of DLQ matches that of Correlation Statistical Queries (CSQ) only for specific loss functions like squared loss. However, simpler loss functions such as l1 loss show DLQ achieving the same complexity as SQ. Furthermore, they show that DLQ can capture the learning complexity with stochastic gradient descent using a two-layer neural network model. This provides a unified theoretical framework for analyzing gradient-based learning of sparse functions, highlighting the importance of loss function selection and offering valuable insights for researchers in optimization algorithms and deep learning.
Key Takeaways#
Why does it matter?#
This paper is important as it bridges the gap between theoretical analysis and practical gradient-based learning. It provides a novel framework for analyzing the complexity of gradient algorithms for learning sparse functions. The findings are highly relevant to researchers working on optimization algorithms, high-dimensional statistics, and deep learning, potentially inspiring future research on efficient gradient methods and better understanding of generalization.
Visual Insights#

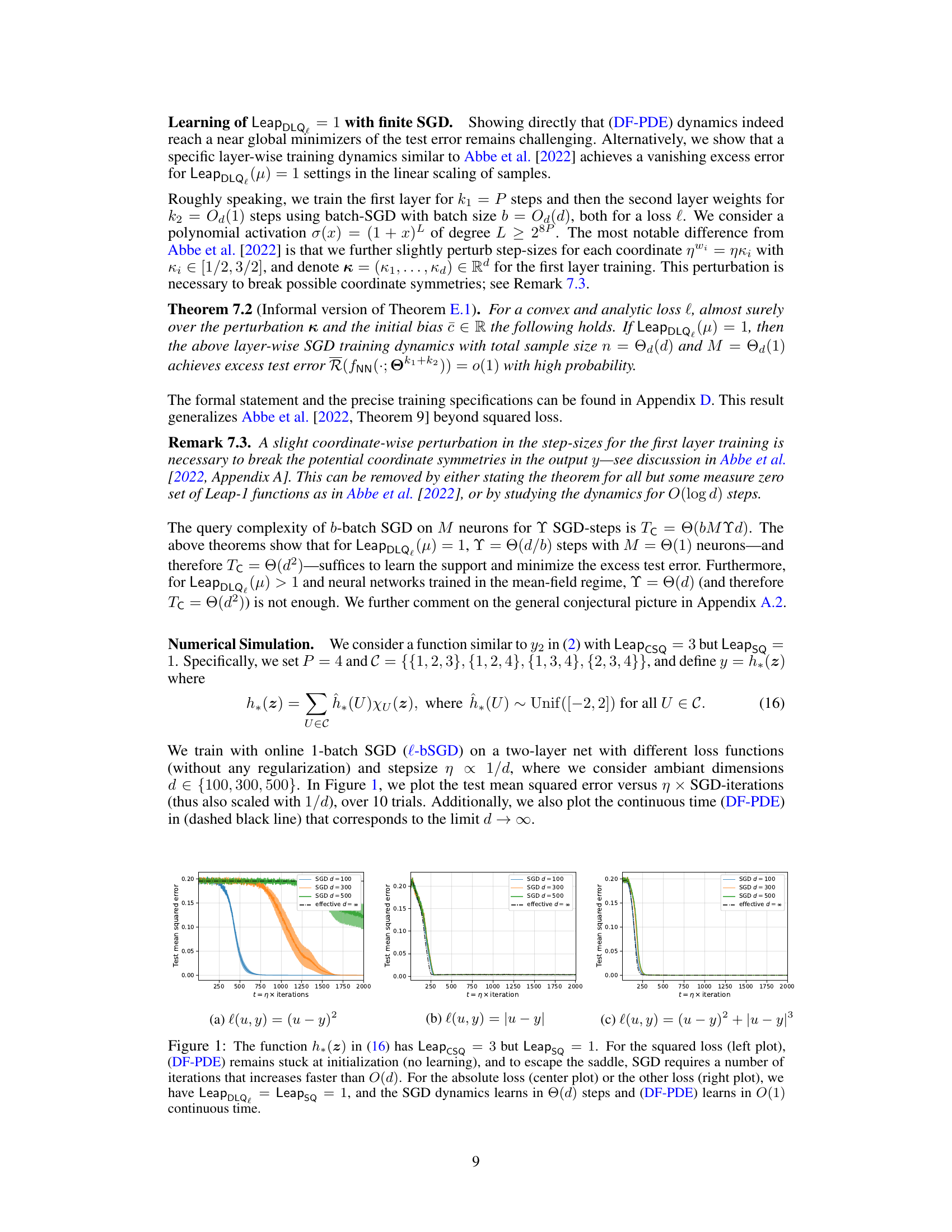
This figure shows the training dynamics of online SGD with different loss functions for a junta learning problem, where the target function depends on a subset of coordinates. The x-axis represents the number of iterations, and the y-axis represents the test mean squared error. The results demonstrate the effect of the loss function on the convergence of SGD. For the squared loss, the training dynamics gets stuck in a saddle point and does not converge. However, for the absolute loss, SGD converges in O(d) iterations, aligning with the theoretical analysis. The figure also compares the SGD dynamics to a continuous-time mean-field model (DF-PDE).

This table summarizes the complexity results of learning sparse functions using different query types: Statistical Queries (SQ), Correlation Statistical Queries (CSQ), and Differentiable Learning Queries (DLQ). It shows how the query complexity (number of queries needed) scales with the input dimension (d) for both adaptive (queries depend on previous answers) and non-adaptive (queries are fixed in advance) algorithms. The complexity is expressed in terms of a leap exponent (adaptive) or cover exponent (non-adaptive), which are determined by the structure of ‘detectable’ subsets of coordinates, which in turn depends on the query type and loss function used.
Full paper#