↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Contextual MNL bandits are used for sequential assortment selection problems, but there’s been a significant gap between theoretical lower and upper bounds on the regret (performance loss) of learning algorithms, especially concerning the maximum assortment size. Existing algorithms either lack efficiency or fail to achieve the optimal regret. This problem is further complicated by variations in reward structures across different algorithms.
This paper introduces OFU-MNL+, a computationally efficient algorithm that achieves a matching upper bound to the established lower bound, demonstrating near-minimax optimality. This is done by establishing tight regret bounds for both uniform and non-uniform reward scenarios. The algorithm’s efficiency stems from an online parameter estimation technique coupled with an optimistic assortment selection approach. The findings show that the algorithm is efficient and improves regret as the assortment size K increases, unless the attraction parameter for the outside option vo scales linearly with K, providing valuable insights into assortment selection problems and efficient learning algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial because it resolves a long-standing open problem in contextual multinomial logit (MNL) bandits: the discrepancy between upper and lower regret bounds. It offers a computationally efficient algorithm, providing a practical solution for real-world applications and guiding future research toward minimax optimality.
Visual Insights#
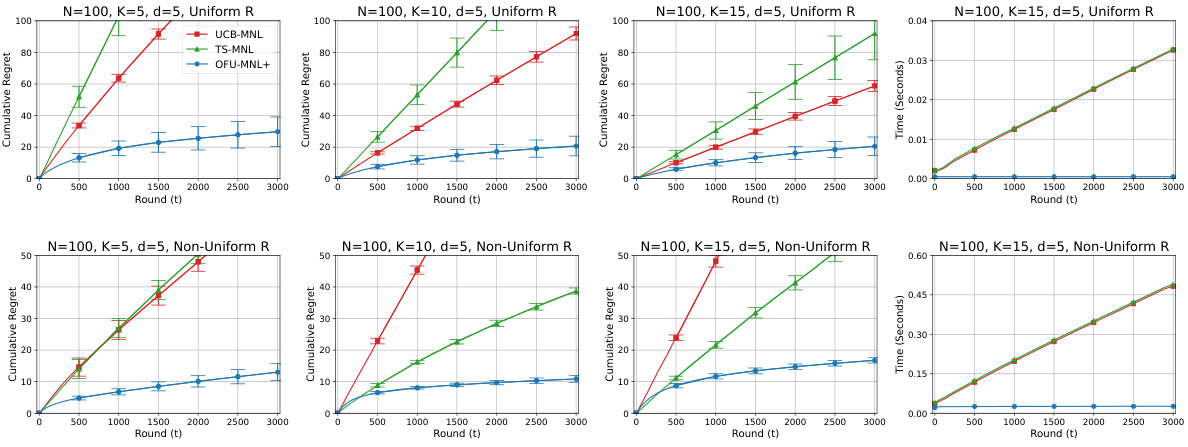
This figure displays the performance of three different algorithms (UCB-MNL, TS-MNL, and OFU-MNL+) in terms of cumulative regret and runtime per round. The results are shown for both uniform and non-uniform reward settings, with different assortment sizes (K=5, 10, 15). The left three graphs show cumulative regret for each setting, and the rightmost graph shows runtime per round for K=15. This allows for a direct comparison of the algorithms’ performance under various conditions.

This table compares the lower and upper regret bounds of different algorithms for the contextual multinomial logit (MNL) bandit problem. It considers variations in problem settings (contexts, rewards, and the attraction parameter for the outside option, (v_0)), and reports the computational cost per round for each algorithm. The table highlights the gap between existing lower and upper bounds and the contributions of the current work in closing this gap.
In-depth insights#
MNL Bandit Regret#
MNL (Multinomial Logit) bandit regret quantifies the performance of algorithms in sequential decision-making problems where user choices follow an MNL model. Lower bounds on regret establish theoretical limits on achievable performance, while upper bounds demonstrate the performance guarantees of specific algorithms. A significant challenge in MNL bandit research is the gap between these bounds, particularly concerning the influence of assortment size (K) and reward structure (uniform vs. non-uniform). Recent work focuses on developing algorithms that achieve near-minimax optimality, meaning their regret matches the lower bound up to logarithmic factors. This optimality often depends on computationally efficient methods, addressing the need for algorithms that are both theoretically sound and practically applicable. Contextual MNL bandits, extending the problem to include user-specific information, add further complexity and necessitate sophisticated algorithm designs to mitigate the impact of the increased dimensionality.
OFU-MNL+ Algorithm#
The OFU-MNL+ algorithm stands out for its computational efficiency and near minimax optimality in addressing contextual multinomial logit (MNL) bandits. Unlike previous algorithms struggling with computational complexity or suboptimal regret bounds, OFU-MNL+ employs an efficient online mirror descent approach for parameter estimation. This clever strategy avoids the computationally expensive maximum likelihood estimation and allows for a constant-time update. Furthermore, the algorithm’s design cleverly incorporates upper confidence bounds, striking a balance between exploration and exploitation to achieve near-optimal regret. Crucially, OFU-MNL+ demonstrates improved regret as the assortment size K increases, aligning with intuitive expectations and unlike previous results, providing a significant advance in practical applications of contextual MNL bandits. The theoretical guarantees are further validated through empirical studies confirming its superior performance compared to existing methods.
Reward Structure Impact#
The impact of reward structure on algorithm performance in contextual multinomial logit (MNL) bandits is a critical consideration. Uniform rewards, where all items share the same expected reward, simplify the problem, allowing for tighter theoretical guarantees and potentially more efficient algorithms. However, non-uniform rewards are more realistic in many real-world applications. The transition from uniform to non-uniform rewards significantly impacts the regret bounds, as uniform rewards often lead to algorithms with better regret bounds that scale favorably with assortment size. This is because uniform rewards provide a more structured learning environment with more readily available information. Understanding this shift and developing robust algorithms that perform well under both scenarios is crucial for practical deployment. This often involves a trade-off between theoretical optimality and computational efficiency, since instance-dependent bounds may be necessary to capture the complexity introduced by varying rewards. Therefore, future research should focus on designing algorithms that explicitly adapt to diverse reward structures, achieving near-optimal regret while remaining computationally efficient.
Minimax Optimality#
Minimax optimality, a crucial concept in decision theory, seeks to find strategies that perform well under the worst-case scenarios. In the context of machine learning, especially in online learning settings like bandits, it aims to minimize the maximum possible regret. A minimax optimal algorithm guarantees a regret bound that is the best possible, considering all possible problem instances. The research paper likely explores the contextual multinomial logit (MNL) bandit problem, aiming to prove the minimax optimality of a novel algorithm. This involves demonstrating both a matching upper and lower bound on the regret, showing that no other algorithm can achieve a significantly better performance. Achieving minimax optimality is a significant contribution because it establishes the fundamental limits of performance for the given problem. The paper likely provides theoretical guarantees and possibly empirical evaluations to support their claims. The computational efficiency of the proposed minimax optimal algorithm is also a critical factor, as many optimal algorithms are computationally intractable. Therefore, the results presented would represent a significant theoretical advancement with practical implications.
Future Research#
Future research directions stemming from this paper could explore several promising avenues. Extending the OFU-MNL+ algorithm to handle more complex reward structures beyond uniform and non-uniform settings is crucial. This might involve incorporating nuanced reward functions or considering scenarios with dynamic reward changes over time. Investigating the impact of different outside option attraction parameters (v0) on regret bounds under diverse reward models requires further attention. The current analysis provides valuable insights but leaves some questions unanswered. Developing tighter instance-dependent regret bounds for both uniform and non-uniform reward scenarios would enhance the theoretical understanding. Additionally, exploring alternative algorithmic approaches, such as those based on Thompson Sampling or other exploration strategies, could reveal potential improvements in efficiency or regret performance. Finally, and perhaps most importantly, rigorous empirical evaluations on large-scale real-world datasets are necessary to validate the theoretical findings and demonstrate the practical efficacy of the proposed OFU-MNL+ algorithm in diverse contexts.
More visual insights#
More on figures

This figure shows the cumulative regret and runtime per round for three different assortment sizes (K=5, 10, 15) under both uniform and non-uniform reward settings. The left three plots display the cumulative regret, while the rightmost plot shows the runtime per round for K=15. The top row represents uniform rewards, and the bottom row represents non-uniform rewards. The results visually demonstrate the performance of the OFU-MNL+ algorithm compared to UCB-MNL and TS-MNL across different settings.
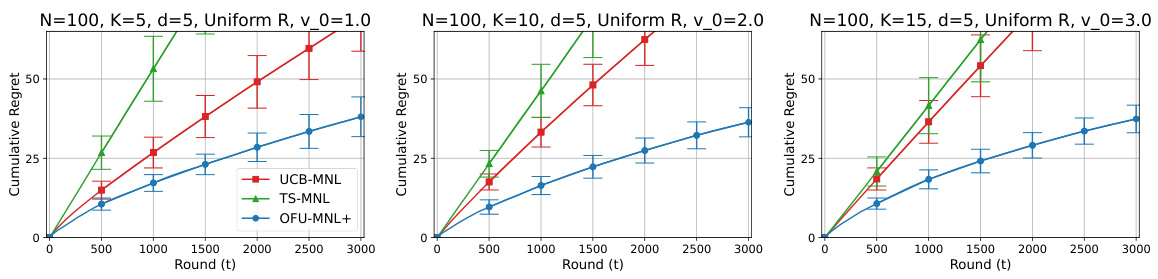
This figure presents the comparison results for cumulative regret and runtime per round for three algorithms: UCB-MNL, TS-MNL, and OFU-MNL+. The results are shown for different assortment sizes (K = 5, 10, 15) under both uniform and non-uniform reward settings. The left three plots illustrate the cumulative regret over 3000 rounds, while the rightmost plot displays the runtime per round for K=15. The results show that OFU-MNL+ consistently outperforms UCB-MNL and TS-MNL in terms of cumulative regret, and maintains a constant runtime per round, unlike the other two algorithms. The figure also visually demonstrates that increasing the assortment size K leads to reduced regret under the uniform reward setting but not under non-uniform rewards.
Full paper#



















