Protected Test-Time Adaptation via Online Entropy Matching: A Betting Approach

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on test-time adaptation and domain generalization in machine learning. It offers a novel approach that addresses the limitations of existing methods, enhancing robustness and accuracy in real-world scenarios. The proposed method, with its unique self-supervised mechanism, provides a valuable contribution, opening exciting avenues for future research. This includes developing more robust and efficient online learning techniques and exploring its application to various domains and tasks.

Visual Insights

#

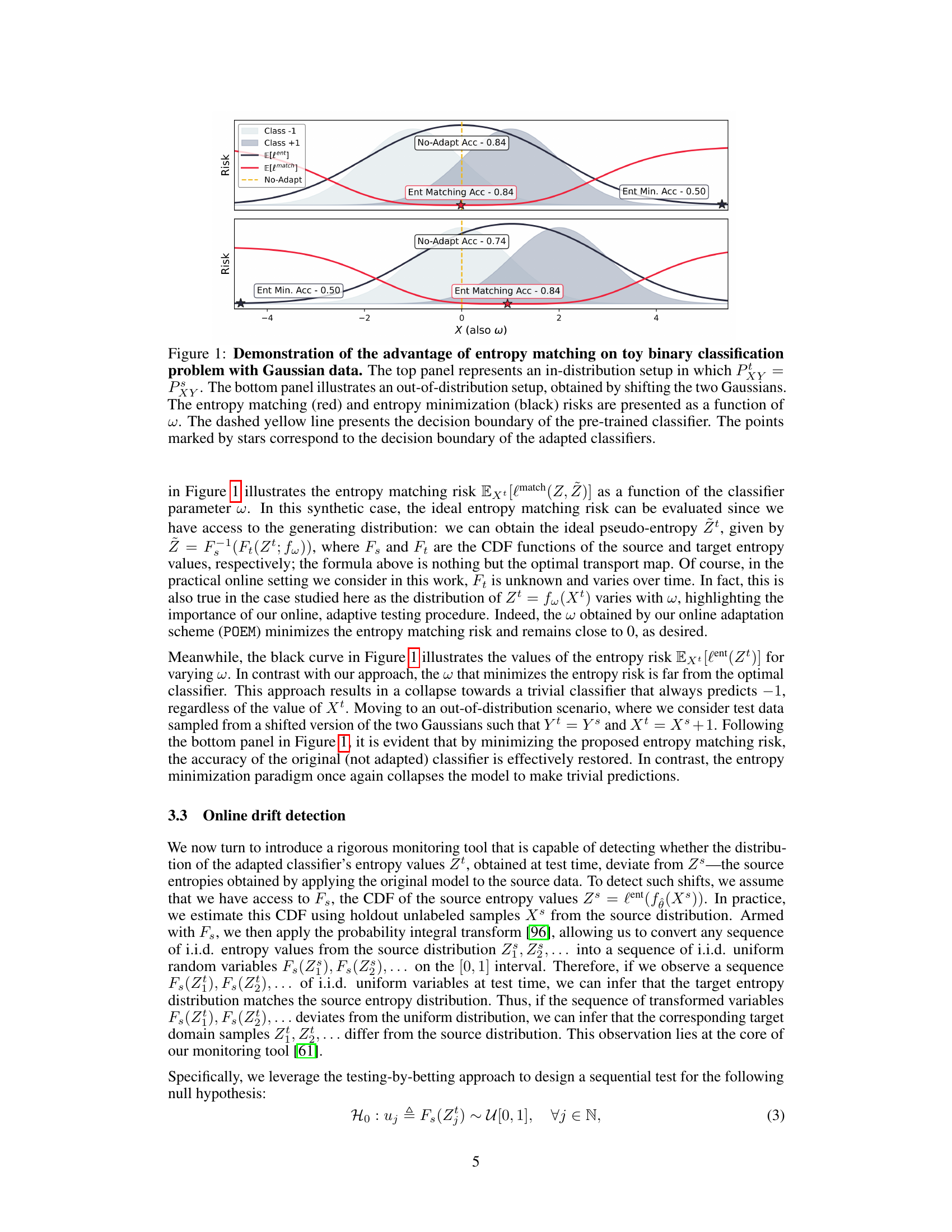
This figure compares two loss functions, entropy minimization and entropy matching, in a simple binary classification problem with Gaussian data. The top panel shows an in-distribution scenario, where the source and target data distributions are the same; both loss functions maintain high accuracy. The bottom panel illustrates an out-of-distribution scenario, where the target distribution has shifted. Entropy minimization leads to a collapse in performance, while entropy matching maintains high accuracy by adapting the decision boundary.

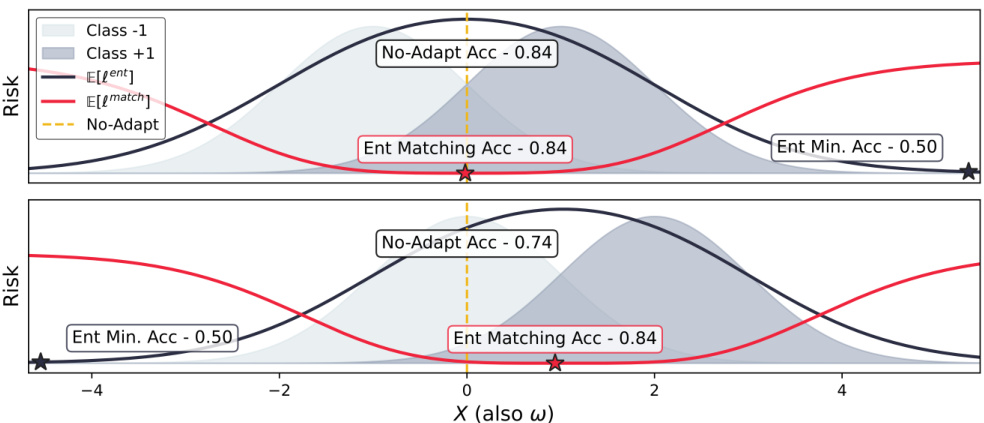
This table presents the average test-time adaptation accuracy results on ImageNet-C dataset for different methods. The accuracy is calculated over all 15 corruption types at severity level 5. COTTA’s lower performance is attributed to its learning rate being optimized for the continual shift setting.

In-depth insights

#

Online Entropy Match

#

Online entropy matching is a novel test-time adaptation technique that dynamically adjusts a classifier’s parameters to match the entropy distribution of the source domain. Unlike traditional self-training approaches that solely focus on minimizing entropy, which can lead to overconfidence, this method incorporates an online statistical framework to detect distribution shifts. This detection triggers an adaptive mechanism that updates model parameters, driving the test-time entropy distribution to match that of the source domain. This process builds robustness to distribution shifts while maintaining accuracy in their absence. The method leverages concepts from betting martingales and optimal transport to achieve fast reactions to shifts and an effective parameter updating strategy, respectively. Experiments demonstrate improved test-time accuracy and calibration compared to existing entropy minimization methods, showcasing its effectiveness in various scenarios. The core idea is to use entropy, but to control the adaptation process using a statistical test and optimal transport, rather than only focusing on loss minimization.

Betting Martingale Test

#

A betting martingale test, in the context of a research paper on protected online entropy matching for test-time adaptation, likely involves a sequential hypothesis test framed as a gambling game. The null hypothesis would represent no distribution shift in the test data’s entropy values compared to the training data. The test statistic is the wealth accumulated through a series of bets, where each bet is placed based on the observed entropy of a new test sample. The betting strategy is crucial; it dictates the magnitude of each bet based on past observations. A successful betting strategy would lead to rapid wealth growth under the alternative hypothesis (a distribution shift), while remaining relatively stable under the null hypothesis. The martingale property ensures fairness, preventing runaway wealth accumulation even when the null is true. This approach offers a robust and principled method for detecting distribution shifts, surpassing methods that rely solely on entropy minimization or thresholding, thus improving test accuracy under distribution shifts while maintaining calibration and accuracy in their absence.

Adaptation Algorithm

#

An adaptation algorithm, in the context of a machine learning model dealing with distribution shifts, dynamically adjusts model parameters to improve performance on unseen data. Online adaptation, a crucial aspect, updates the model incrementally as new data arrives. Self-training, often employed, uses model predictions as pseudo-labels to guide parameter updates. The effectiveness hinges on a balance: minimizing entropy to boost accuracy while preventing overconfidence or model collapse. Online drift detection mechanisms play a vital role, flagging distribution shifts and triggering adaptation only when necessary, thus maintaining performance on stable data and preventing unnecessary model updates. A sophisticated adaptation algorithm will seamlessly integrate these components, leveraging statistical testing and optimization methods for robustness and efficiency. Optimal transport, a mathematical concept, might be incorporated to efficiently map the test-time data distribution closer to the training distribution, improving the effectiveness of adaptation.

Empirical Evaluation

#

An Empirical Evaluation section in a research paper would rigorously assess the proposed method’s performance. This would involve selecting relevant datasets, establishing appropriate evaluation metrics (like accuracy, precision, recall, F1-score, etc.), and comparing the results against existing state-of-the-art methods. Careful consideration of experimental design is crucial; this includes the choice of datasets representative of real-world scenarios, controlling for confounding variables, and ensuring sufficient sample sizes. The analysis should go beyond simple performance metrics, investigating aspects like model robustness, sensitivity to hyperparameter choices, and computational efficiency. A strong Empirical Evaluation would also include error bars and statistical significance tests to support the claims made. Visualization of results using graphs and tables improves clarity and facilitates the understanding of trends and comparisons. Finally, the discussion should acknowledge any limitations and propose future directions for improvements.

Future Work

#

The authors suggest several promising avenues for future research. A theoretical analysis to solidify the empirical findings and explore the precise conditions under which entropy matching surpasses minimization is crucial. Addressing label shift at test time, a situation where the source and target domains have differing label distributions, is another significant challenge. They propose two potential solutions: a prediction-balanced reservoir sampling technique and a weighted source CDF approach to improve the method’s robustness to these imbalances. Finally, they suggest investigating the use of alternative entropy measures, such as Tsallis entropy, or cross-entropy, to enhance the method’s adaptability and flexibility in various scenarios. This multifaceted future work plan demonstrates a commitment to further solidifying and expanding the capabilities of their proposed approach.

More visual insights

#

More on figures

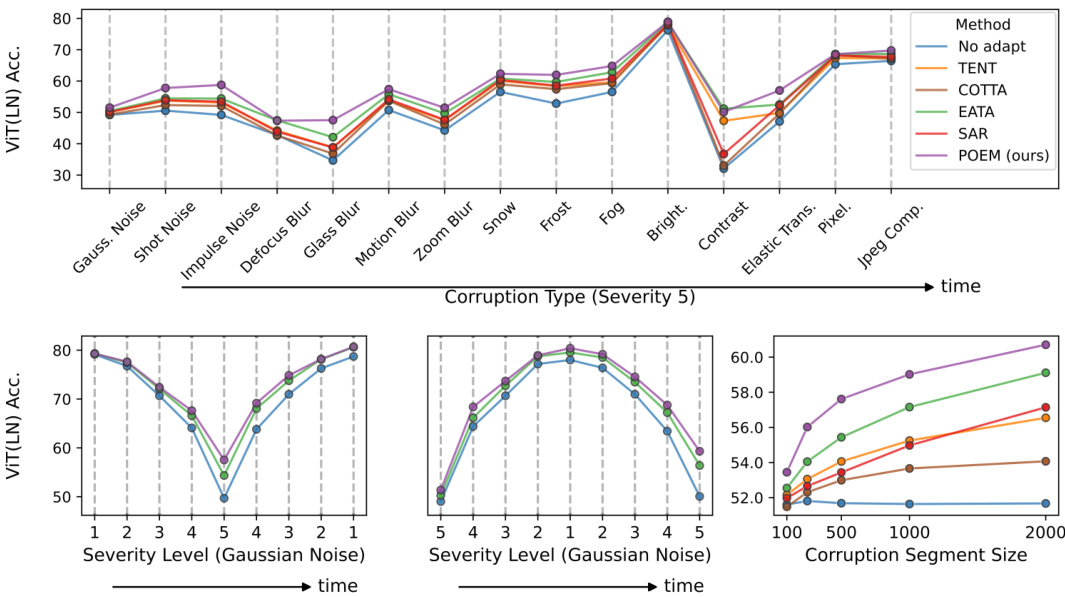
This figure shows the results of continual test-time adaptation experiments on the ImageNet-C dataset using a Vision Transformer (ViT) model. The top panel displays the per-corruption accuracy with a corruption segment size of 1000 examples. The bottom-left and bottom-center panels show the accuracy changes under severity shifts, while the bottom-right panel shows the mean accuracy as a function of the corruption segment size. The figure demonstrates POEM’s performance compared to the best baseline method (EATA) and a no-adaptation approach across various scenarios.

The left panel shows the calibration error (ECE) and parameter change (||w||) for different adaptation methods on the ImageNet dataset. Lower values indicate better calibration and less modification to the original model parameters. The right panel shows the betting variable (e) over time for both in-distribution and out-of-distribution scenarios. This variable controls the aggressiveness of the bets in the testing-by-betting framework, and its behavior reflects the adaptation process.

This figure shows the behavior of the wealth process (martingale) and the betting variable epsilon in three different scenarios: in-distribution, out-of-distribution without adaptation, and out-of-distribution with adaptation. The top panel displays the martingale in log scale, while the bottom panel shows epsilon. The results demonstrate that the proposed adaptation mechanism effectively controls the martingale’s growth in the presence of distribution shift, preventing excessive model updates.

This figure presents the results of continual test-time adaptation experiments conducted on ImageNet-C using a Vision Transformer (ViT) model. The top panel shows per-corruption accuracy with a corruption segment size of 1000 examples. The bottom-left and bottom-center panels illustrate the effect of severity shifts on accuracy. The bottom-right panel demonstrates how the mean accuracy changes as a function of corruption segment size.

This figure shows the cumulative distribution function (CDF) of the entropy of the predictions made by different test-time adaptation methods on ImageNet data. The left panel shows the results when the models are tested on in-distribution data (ImageNet validation set) and the right panel shows the results when tested on out-of-distribution data (ImageNet-C with brightness corruption). The dotted black line represents the CDF of the entropy of the original model’s predictions on the source data. The figure demonstrates how the different methods affect the distribution of the test entropy. The goal of protected online entropy matching (POEM) is to have the target entropy distribution match the source entropy distribution to maintain robustness against distribution shifts.

The figure shows the results of continual test-time adaptation experiments conducted on the ImageNet-C dataset using a Vision Transformer (ViT) model. The top panel displays the per-corruption accuracy for different corruption types at severity level 5, with a corruption segment size of 1000 examples. The bottom left and center panels illustrate the accuracy changes during severity shifts (low to high and back to low, and high to low and back to high). The bottom right panel shows the mean accuracy as a function of the corruption segment size, demonstrating the effect of segment size on the adaptation performance.

This figure shows the results of continual test-time adaptation experiments on the ImageNet-C dataset using a Vision Transformer (ViT) model. The top panel displays per-corruption accuracy with a segment size of 1000 examples. The bottom-left and bottom-center panels illustrate the accuracy changes under severity shifts (low to high and back, and high to low and back). The bottom-right panel shows how mean accuracy changes with different corruption segment sizes. Only POEM, EATA, and the no-adaptation baseline are shown for clarity.

This figure presents the results of continual test-time adaptation experiments on the ImageNet-C dataset using a Vision Transformer (ViT) model. The top panel shows the per-corruption accuracy with a corruption segment size of 1000 examples, averaged over 10 independent runs. The bottom panels illustrate the accuracy changes under different severity shift scenarios (low to high and back, high to low and back) for gaussian noise, comparing POEM with EATA and the no-adaptation baseline. The bottom-right panel displays the mean accuracy under continual corruptions as the corruption segment size varies.

More on tables

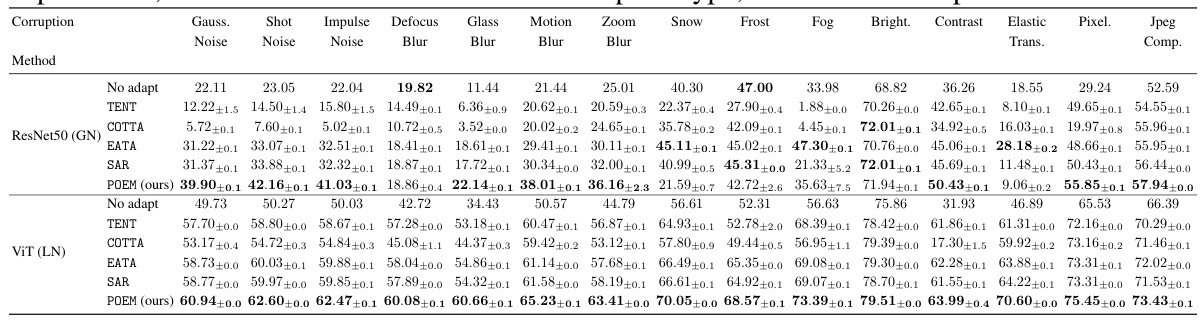
This table presents a detailed breakdown of the performance of different test-time adaptation methods on the ImageNet-C dataset. It shows the accuracy achieved by each method for each of the 15 different corruption types at severity level 5. The results are averaged over 10 independent experimental runs, and standard errors are included to show variability.

This table presents the results of applying different test-time adaptation methods to the ImageNet validation set (in-distribution data). It compares the top-1 and top-5 accuracy, empirical calibration error (ECE), and the change in model parameters (||w||) for each method. Lower values for ECE and ||w|| indicate better performance and less modification to the original model.

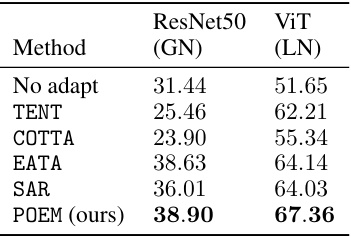
This table presents the average accuracy of different test-time adaptation methods on ImageNet-C dataset when facing a single corruption type at severity level 5. It shows the performance of several methods including the proposed POEM method and baselines like TENT, COTTA, EATA, and SAR. The table highlights the superior performance of the proposed method compared to the others. Detailed results broken down by each corruption type are available in Table 2.

Full paper

#