The Evolution of Statistical Induction Heads: In-Context Learning Markov Chains

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in deep learning and NLP because it offers a novel approach for understanding the mechanisms of in-context learning in large language models (LLMs). By introducing a simplified, controlled task, it enables more rigorous analysis and provides mechanistic insights into how LLMs learn from context. This opens avenues for developing more efficient and reliable LLMs and advancing our understanding of the capabilities of deep learning models.

Visual Insights

#

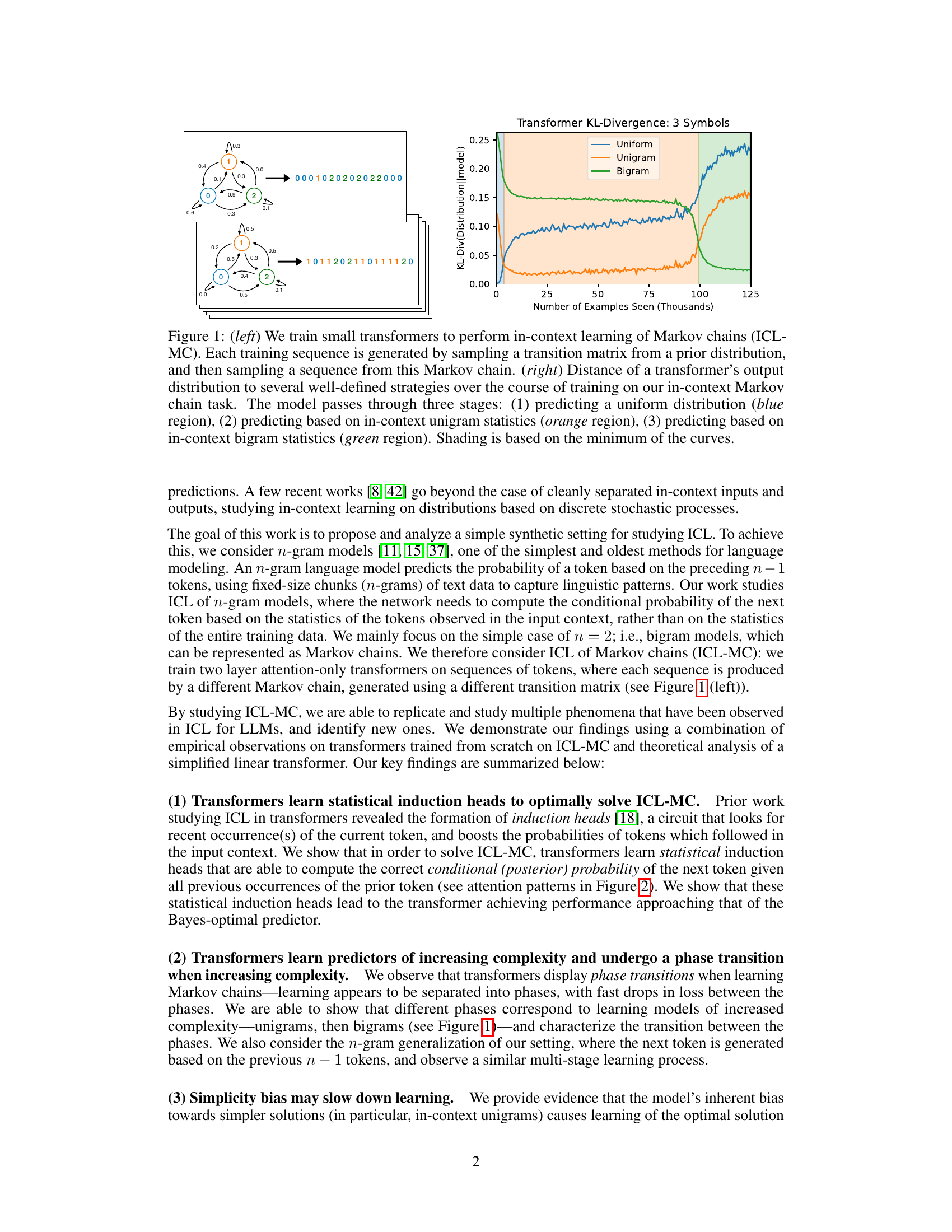
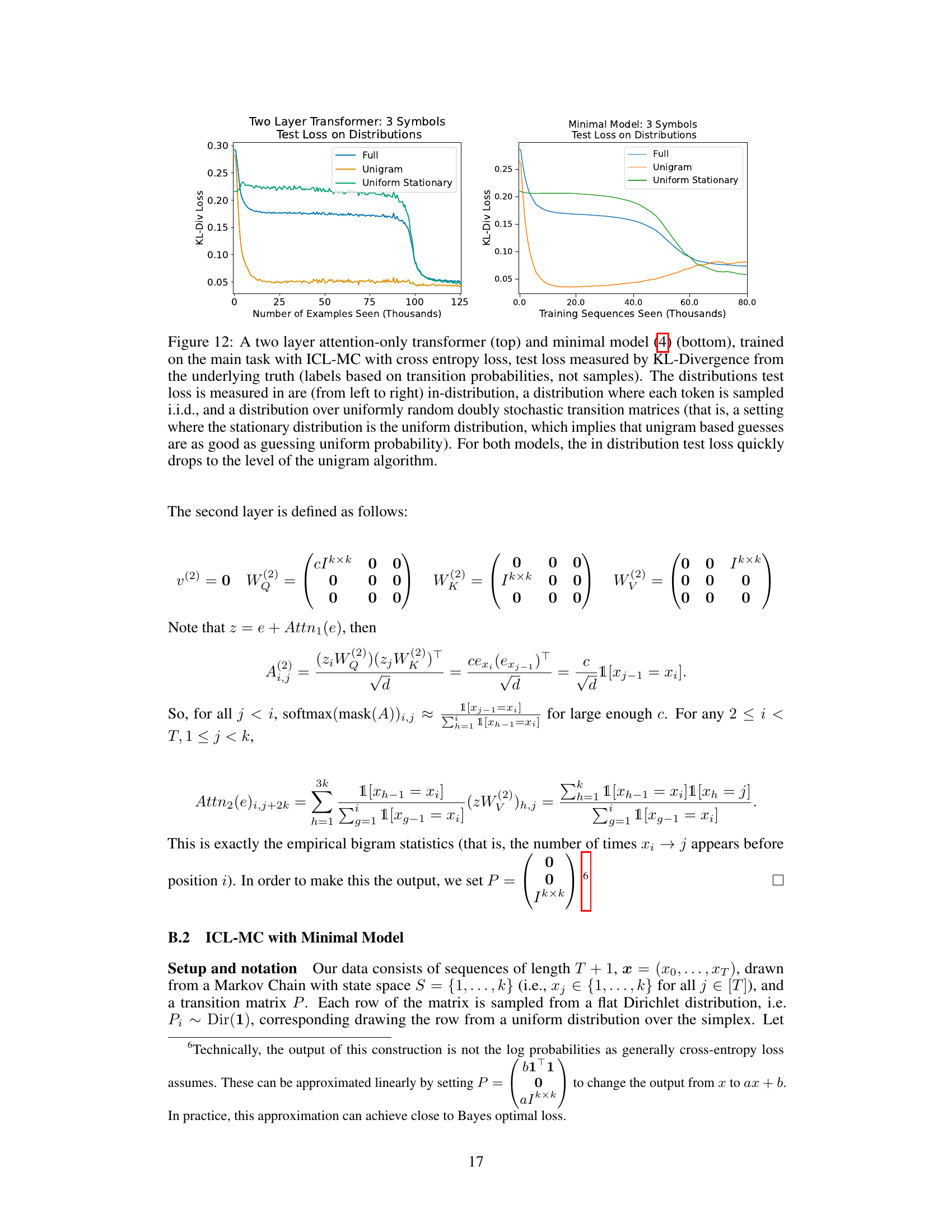
The figure shows the training process of small transformers on an in-context learning task involving Markov chains. The left panel illustrates the task setup, where sequences are generated from randomly sampled Markov chains. The right panel displays the KL divergence between the model’s predictions and three strategies (uniform, unigram, bigram) across training iterations. It reveals a multi-phase learning process, starting with uniform predictions, then transitioning to unigram-based predictions, and finally converging to the optimal bigram solution.

In-depth insights

#

ICL-MC Task

#

The ICL-MC task, as described in the paper, is a novel synthetic benchmark designed to investigate the in-context learning capabilities of large language models. It cleverly leverages the simplicity of Markov Chains with random transition matrices, allowing for precise control over data distribution. The task’s core is to predict the next token in a sequence, given prior tokens generated from an underlying Markov chain sampled from a predefined prior distribution. This setup facilitates a nuanced study on how models learn to infer underlying probabilistic patterns. The use of Markov Chains offers a mathematically well-defined structure, making it simpler to analyze learning dynamics than more complex linguistic tasks. Success hinges on the model’s ability to extract the correct bigram statistics and accurately represent the conditional probabilities of the next token, a process of statistical induction, that is directly tested through the evaluation metrics. Moreover, ICL-MC offers a framework for analyzing the emergence of statistical induction heads within transformer networks.

Transformer ICL

#

The heading ‘Transformer ICL’ suggests an investigation into how transformer models perform in-context learning (ICL). The core idea is likely to explore the mechanisms by which transformers learn from examples provided within the input sequence, without explicit training on those specific examples. A key aspect would involve analyzing how the model’s architecture, particularly the attention mechanism, facilitates this ICL. The analysis might explore different phases of learning in transformers, possibly revealing a hierarchical process where simpler patterns are learned before more complex ones. Furthermore, research might focus on the role of induction heads, specialized components within the network that seem critical for ICL. The study might also explore the impact of various factors such as the number of layers, attention heads, and training data distribution on the effectiveness of ICL in transformers. Ultimately, understanding ‘Transformer ICL’ aims to provide a mechanistic understanding of this emergent capability, which is crucial for improving LLMs.

Multi-Phase Learning

#

The concept of “Multi-Phase Learning” in the context of large language models (LLMs) and their in-context learning capabilities is particularly insightful. The paper reveals a hierarchical learning process, where models don’t directly jump to optimal solutions. Instead, they progress through distinct phases, each characterized by a specific level of complexity. Initially, predictions might be essentially random, then transition to relying on simpler, less accurate statistics (like unigrams), before finally reaching the more sophisticated solution (like bigrams). This multi-stage progression is not merely an empirical observation but is supported by theoretical analysis using a simplified model, showing the crucial role of layer interactions and the potential for simpler solutions to hinder the attainment of optimal performance. This phase transition is likely a general phenomenon, not limited to this specific task, and suggests inherent biases in LLMs and their training dynamics. The presence of multiple phases highlights the complex interplay between model architecture, training data, and the inductive biases shaping the learning process. Further research should investigate the generality of these phases and explore strategies to accelerate the transition to optimal performance, potentially bypassing suboptimal solutions.

Simplicity Bias

#

The concept of “Simplicity Bias” in the context of the research paper highlights the tendency of neural networks, particularly in in-context learning scenarios, to initially favor simpler solutions before progressing to more complex, optimal ones. This bias manifests as the model first learning to predict using single-token statistics (unigrams) in the Markov chain task, even though the optimal solution involves bigram statistics. This initial preference for simpler solutions, while seemingly counterintuitive, might stem from the inherent structure and training dynamics of the neural network architecture, causing it to converge on simpler patterns before tackling complex dependencies. The paper suggests that this bias can actually delay the learning of the optimal solution. Modifying the data distribution to reduce the utility of unigram statistics accelerates convergence, showcasing the significant impact of the simplicity bias on learning speed and efficiency. This phenomenon underscores the crucial interaction between the inductive bias inherent in neural networks and the data distribution, underscoring the importance of careful consideration of training data and architecture in achieving optimal in-context learning. Further investigation into the underlying mechanisms and the potential for mitigating this bias could yield valuable insights into improving the performance and efficiency of large language models.

Future of ICL

#

The future of in-context learning (ICL) is brimming with potential. Further research into the mechanisms underlying ICL in large language models (LLMs), particularly the role of induction heads and the interplay between layers, is crucial. This includes investigating how these mechanisms adapt to various data distributions and task complexities. Developing more robust and efficient ICL methods that avoid the pitfalls of simplicity bias and promote faster convergence is also key. Exploring the generalization of ICL beyond simple synthetic tasks to more realistic and complex scenarios in natural language processing will be essential. Finally, addressing the ethical considerations and potential risks of ICL is paramount. This involves developing safeguards to prevent misuse and ensuring fairness and transparency in the application of ICL technology.

More visual insights

#

More on figures

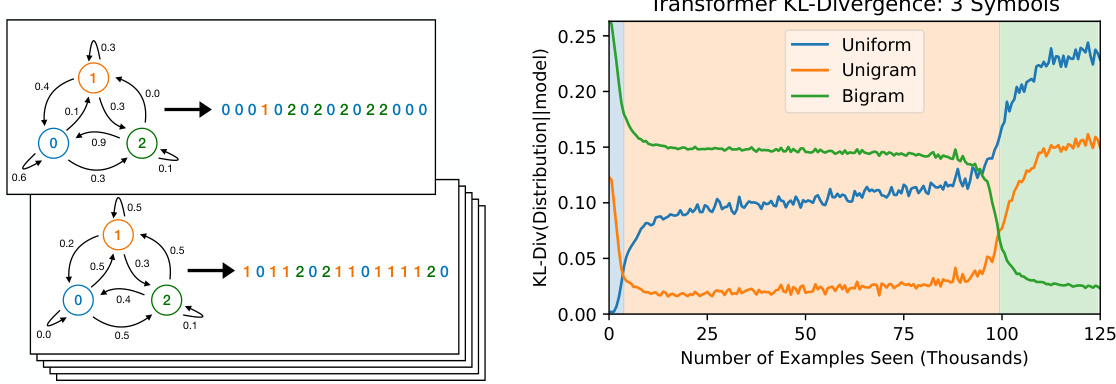
This figure shows the attention patterns of a transformer trained on the ICL-MC task at different stages of training. The intensity of the blue lines represents the attention weights. At the beginning of training, the attention is diffuse. As training progresses, the model learns to focus its attention on relevant tokens, mimicking the bigram calculation process. At the end of training, each token in the first layer attends to the preceding token, while the last token in the second layer attends to the tokens that previously followed it.

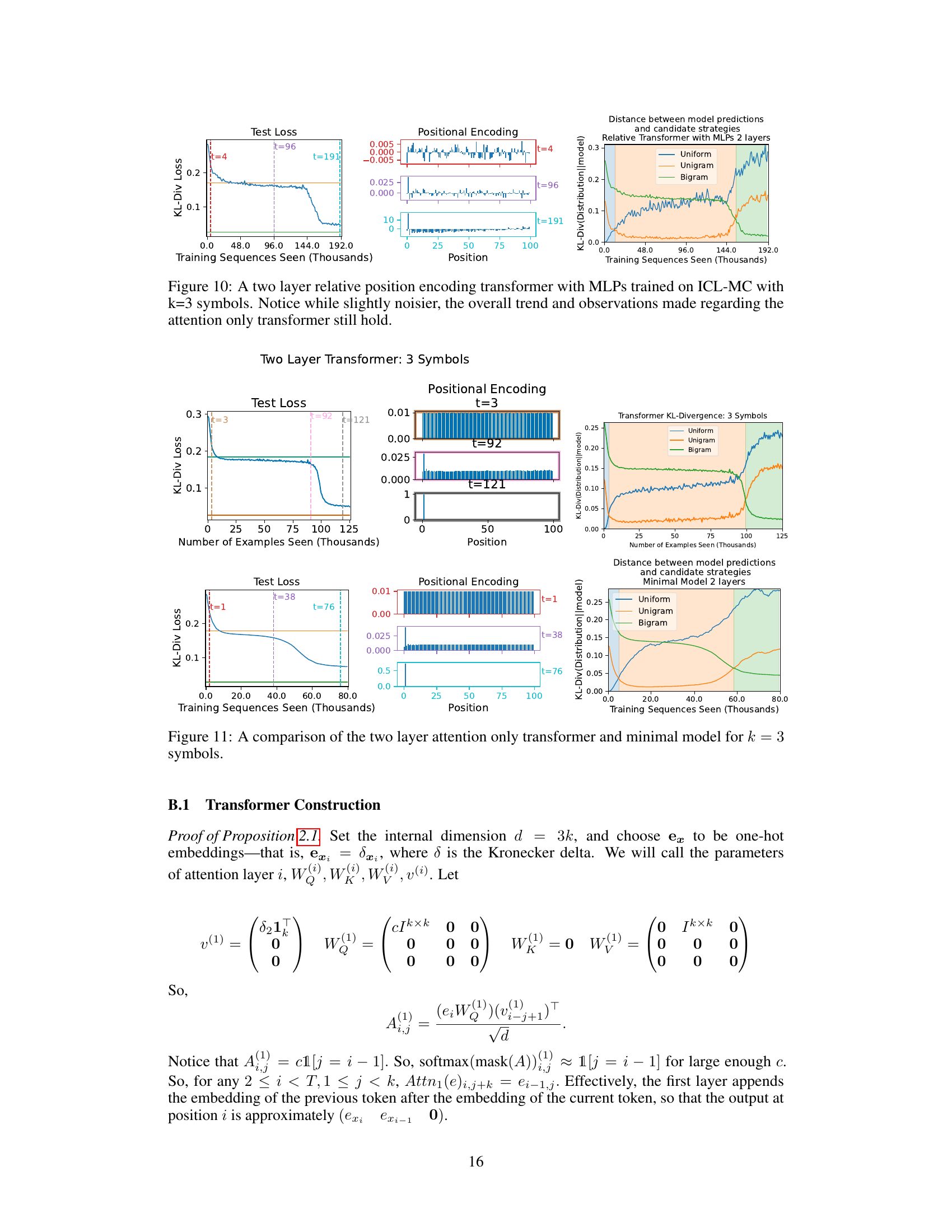
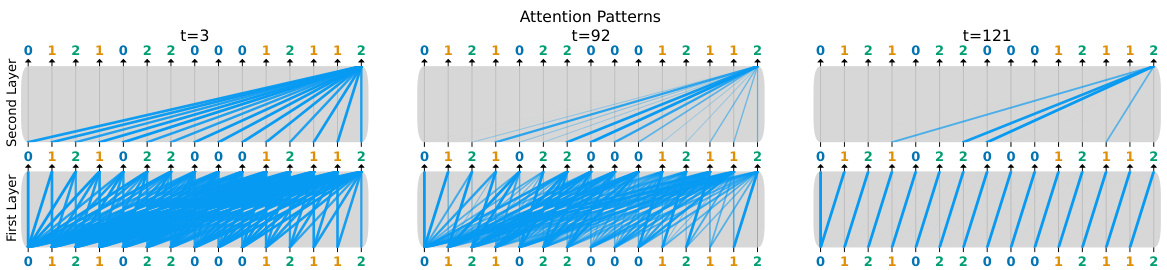
This figure compares the performance of a two-layer transformer and a simplified minimal model on the ICL-MC task. The leftmost graphs show the test loss (KL-divergence from the true distribution) over the course of training, for both models. The orange and green lines represent the loss of the unigram and bigram strategies respectively, providing a benchmark. The center graphs display the positional encoding weights learned by each model. The rightmost graphs show the KL-divergence between the model predictions and the three strategies (uniform, unigram, bigram) across training epochs. This illustrates how the models learn to approximate these strategies over time, with a clear phase transition from unigram to bigram indicated by shading.

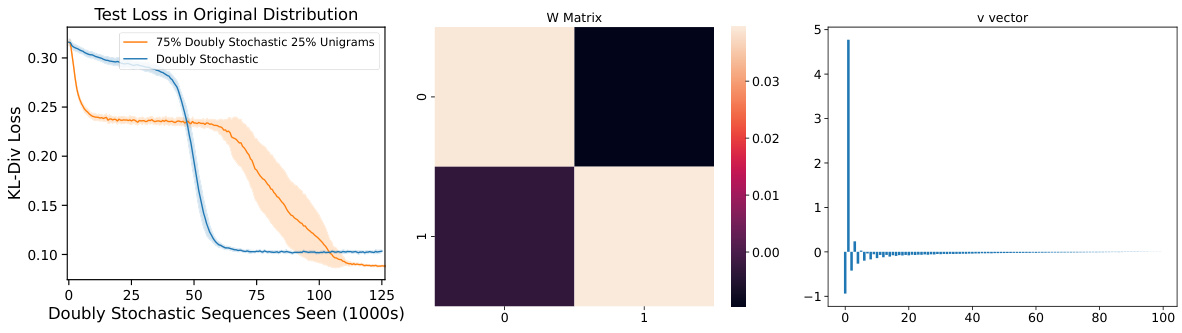
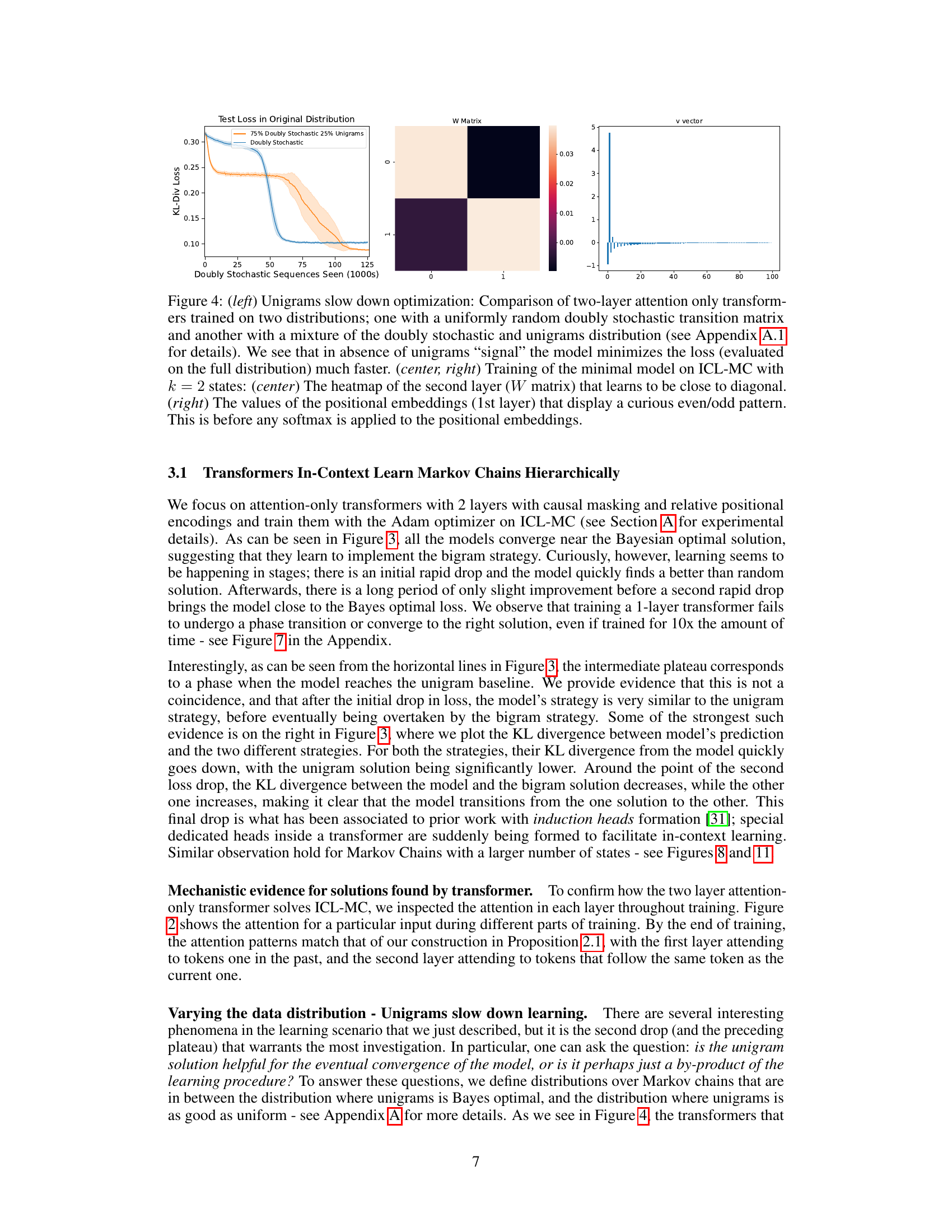
This figure shows that the presence of unigram signals slows down the training process of a two-layer attention-only transformer on the ICL-MC task. The left panel compares the test loss of transformers trained on a purely doubly stochastic distribution and a mixture of doubly stochastic and unigram distributions. The central and right panels illustrate the minimal model’s training dynamics by showing the weight matrix (W) and positional embeddings (v) respectively; illustrating how the minimal model learns to approach the bigram solution, with the W matrix resembling an identity matrix and v showing an alternating positive/negative pattern.

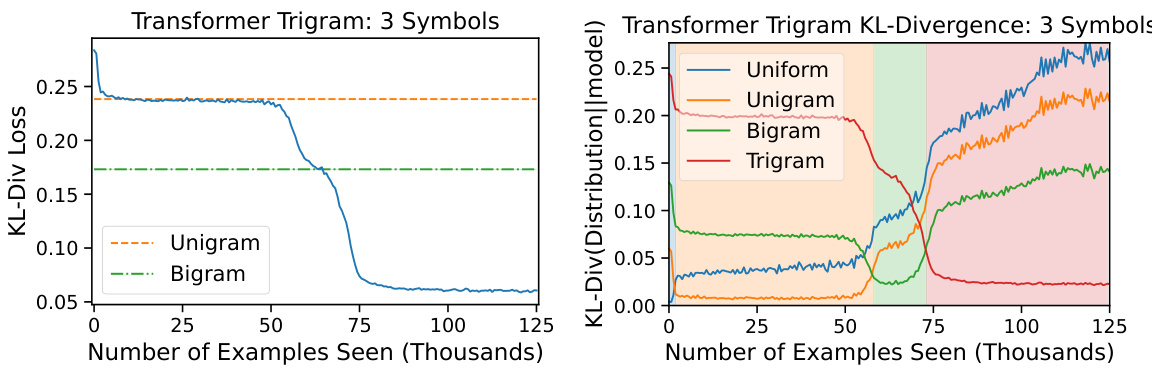
This figure shows the training results of a three-headed transformer on a trigram prediction task. The left panel displays the training loss, which demonstrates a multi-stage learning process with distinct phases of learning. The right panel shows the KL divergence between the model’s predictions and various baselines (uniform, unigram, bigram, and trigram) over the course of training. The KL divergence plot visually illustrates the transition between these stages, confirming that the model progressively learns more complex patterns (from unigram to trigram) during the training process.

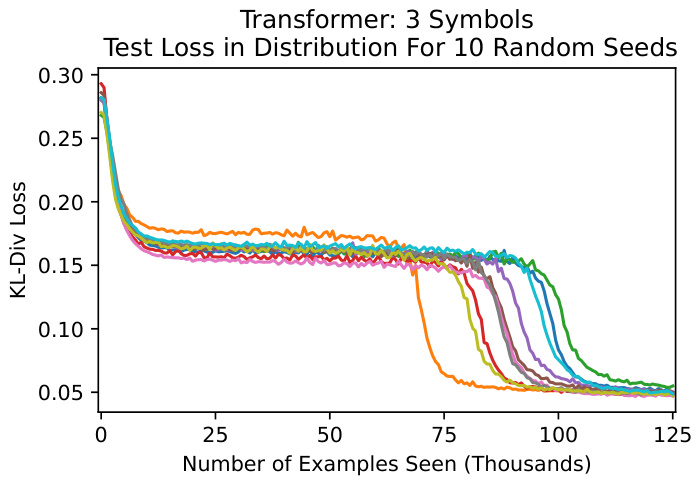
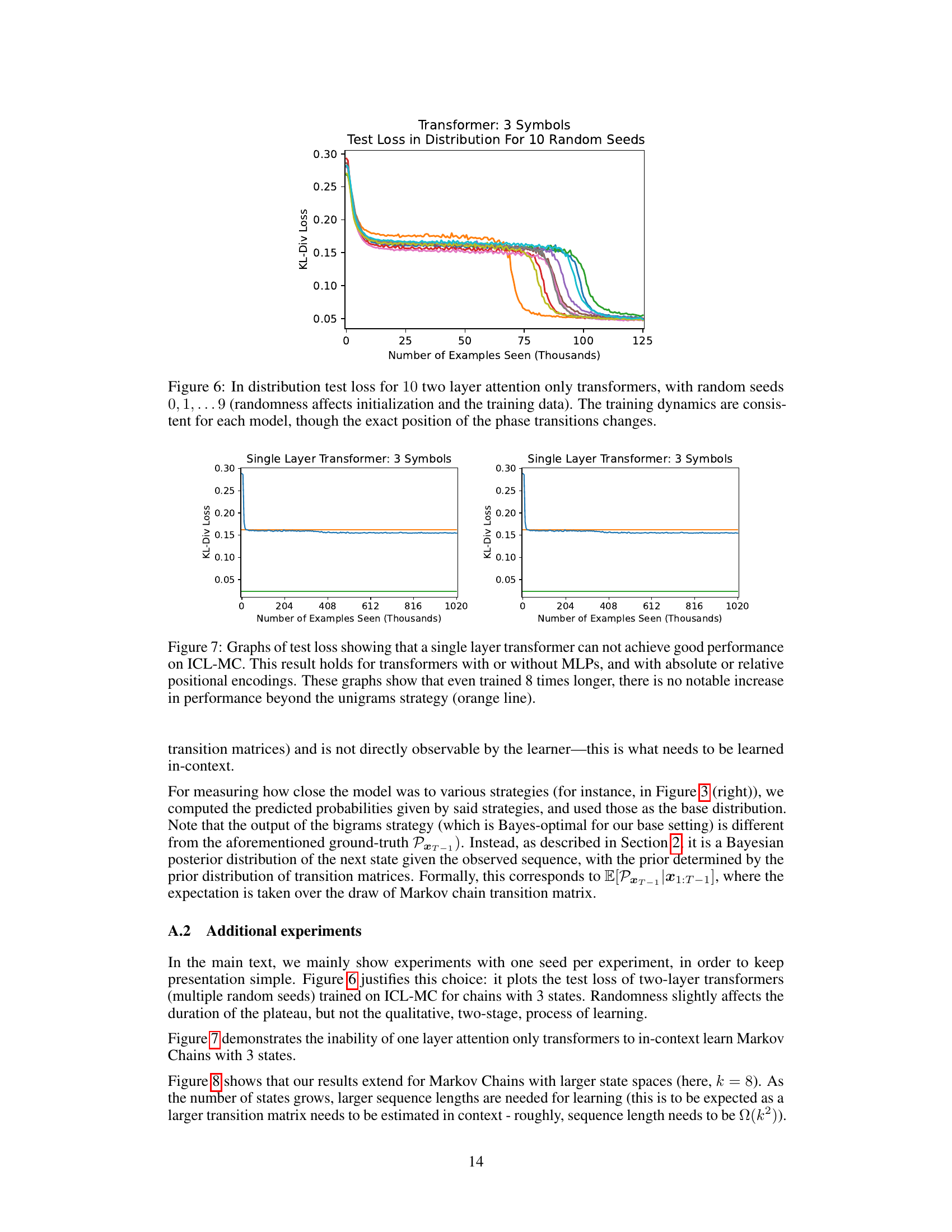
This figure displays the test loss curves for ten different two-layer attention-only transformers trained on the in-context learning of Markov chains task. Each transformer used a different random seed, resulting in variations in the initialization and training data. Despite these variations, the overall training dynamics remain consistent across all ten models, showing a two-phase learning process. The first phase involves a rapid initial drop in the loss, followed by a prolonged period of slow improvement. The second phase is characterized by a sudden, sharp drop in loss, converging towards the optimal solution. Although the exact timing of the phase transitions varies across models, the overall pattern of the two-phase learning process remains consistent.

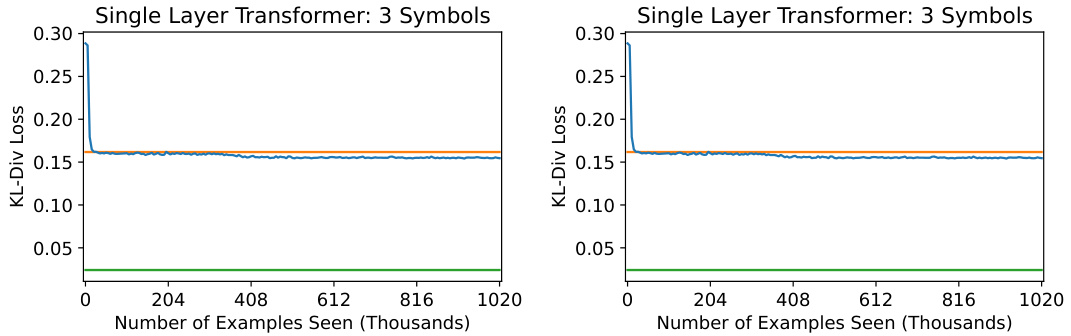
The figure shows the training loss curves for single-layer transformers trained on the in-context learning Markov chain task. Two different single-layer transformer models are shown, each trained for different numbers of epochs. The results demonstrate that single-layer transformers fail to achieve performance better than a simple unigram baseline, even with substantially increased training time. This is evidence that multiple layers are necessary for successfully learning the more complex bigram solution.

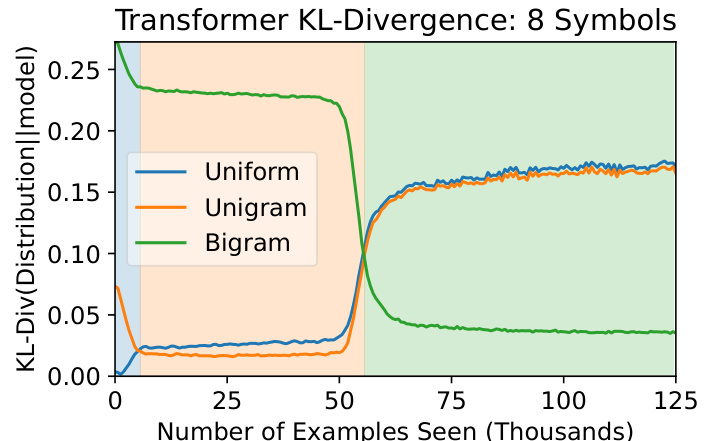
This figure shows the KL-divergence between a transformer model’s predictions and three different strategies (uniform, unigram, and bigram) during training on a Markov Chain task with 8 symbols. The x-axis represents the number of training examples seen, and the y-axis shows the KL-divergence. The figure demonstrates that the model initially learns a suboptimal unigram strategy before transitioning to a more complex bigram strategy. A longer sequence length (200) was needed for the unigram phase to be clearly observable.

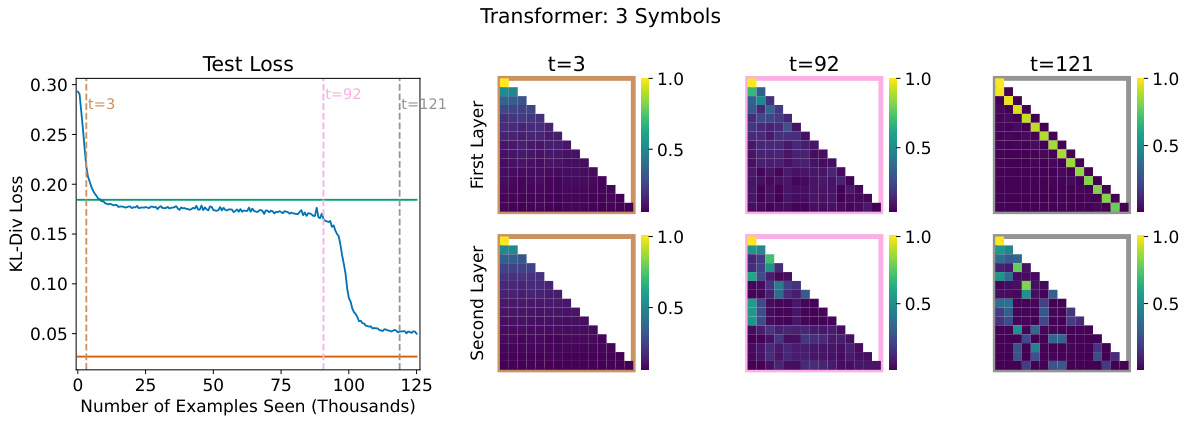
This figure visualizes the attention patterns in a two-layer transformer trained on the In-Context Learning Markov Chains (ICL-MC) task. It shows how the attention weights evolve during training, demonstrating a shift from simpler to more complex strategies. In the initial stage, attention is local, focusing on the previous token. Later, the second layer learns to attend to tokens that followed the same token as the last one, effectively capturing bigram statistics.

The figure compares the performance of a two-layer transformer and a simplified minimal model on an in-context learning task for Markov chains. It shows the test loss over training, highlighting multiple phases in the learning process, with the transition between simpler (unigram) and more complex (bigram) solutions. The effective positional encodings from the transformer and the KL-divergence between models and different strategies are also visualized.

The left panel shows the experimental setup for in-context learning of Markov chains. The right panel shows the KL divergence between the model’s predictions and three different strategies (uniform, unigram, bigram) during training. The figure shows that the model progresses through three phases: initially predicting uniformly, then using unigram statistics, and finally using bigram statistics.

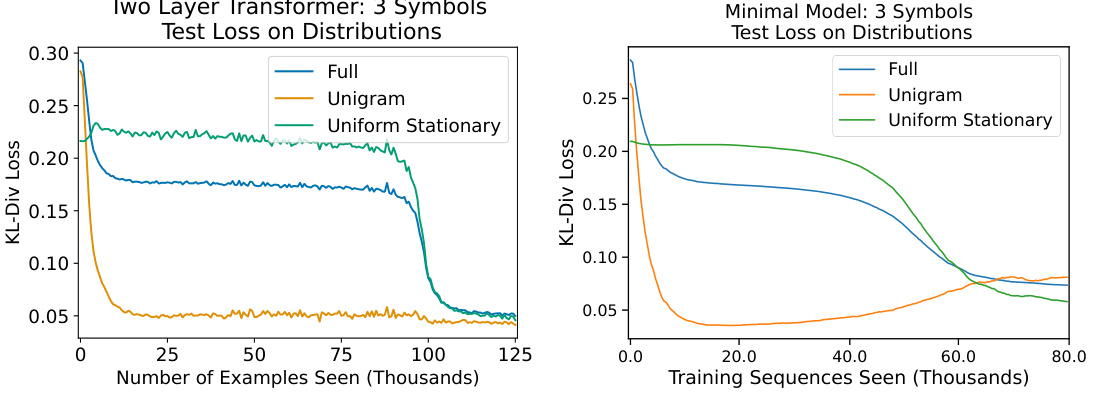
This figure compares the performance of a two-layer transformer and a simplified minimal model on the in-context learning of Markov chains task. It shows the test loss (KL-divergence from the true distribution), the effective positional encoding, and the KL-divergence between model predictions and three strategies (uniform, unigram, and bigram). The results indicate a multi-stage learning process for both models, where they initially learn the simpler unigram strategy before transitioning to the optimal bigram strategy.

Full paper

#