↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world problems involve multiple, often conflicting objectives, requiring careful balancing. Existing multi-objective reinforcement learning (MORL) methods typically rely on predefined preferences, which may be difficult or impossible to obtain. Furthermore, safety is paramount in many applications, requiring constraints on specific actions or outcomes. These challenges limit the applicability of MORL to real-world scenarios.
This paper introduces a novel offline adaptation framework called PDOA that addresses these limitations. PDOA learns a diverse set of policies during training, and adapts a distribution of target preferences at deployment, using only a few demonstrations to implicitly indicate the desired trade-offs and safety constraints. Experimental results show that PDOA effectively infers policies that align with real preferences and satisfy safety constraints, even when safety thresholds are unknown. This makes PDOA a promising tool for real-world applications.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles the challenge of offline multi-objective reinforcement learning (MORL) with constraints, a crucial area for real-world applications. It proposes a novel framework that avoids the need for manually designed preferences, instead leveraging demonstrations to implicitly infer preferences, making it more practical and efficient. The extension to handle safety constraints is also significant, addressing a major limitation in many MORL methods. This work opens avenues for research in adapting MORL to real-world scenarios with multiple conflicting objectives and safety requirements.
Visual Insights#
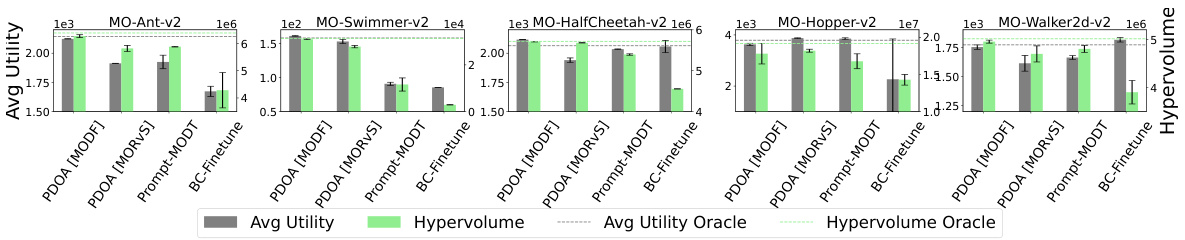
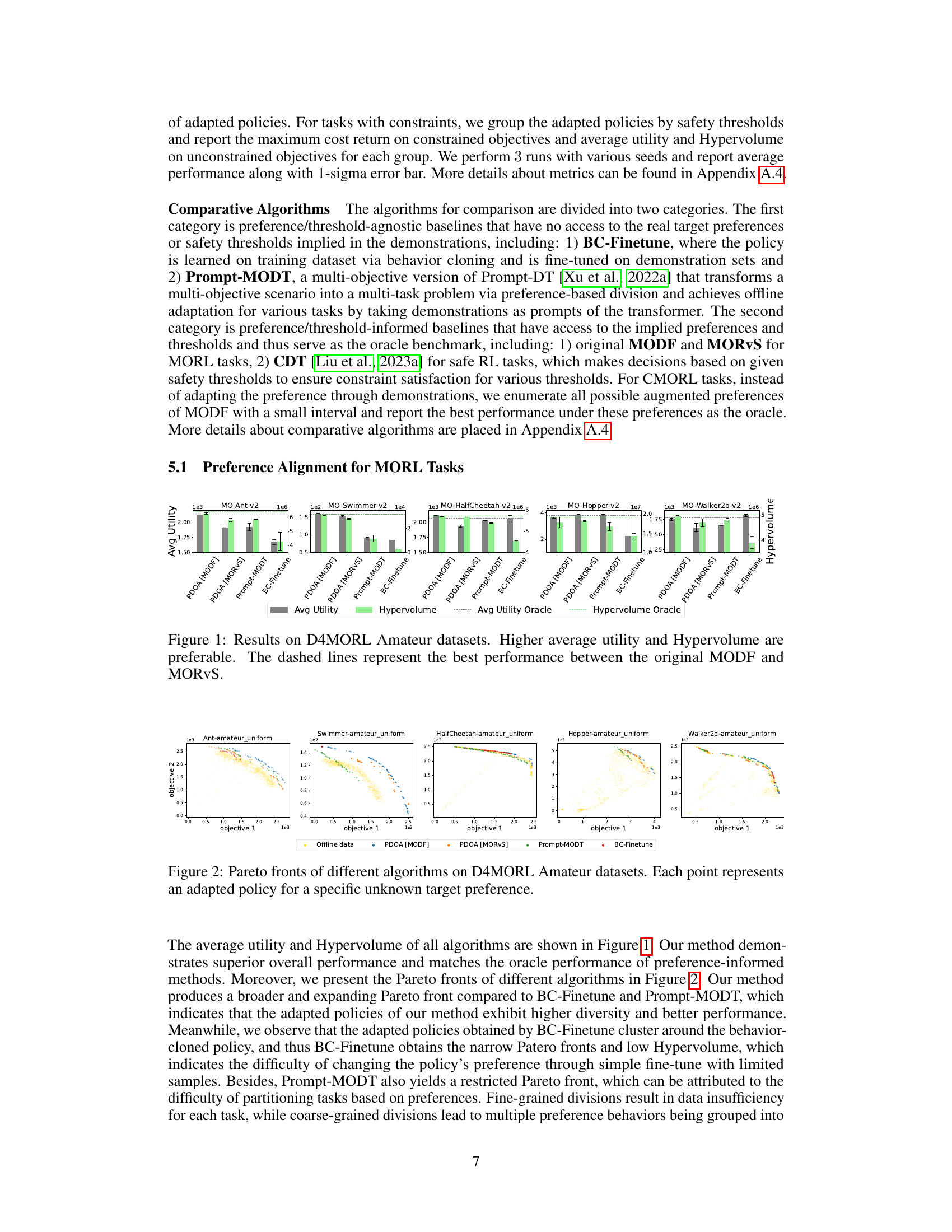
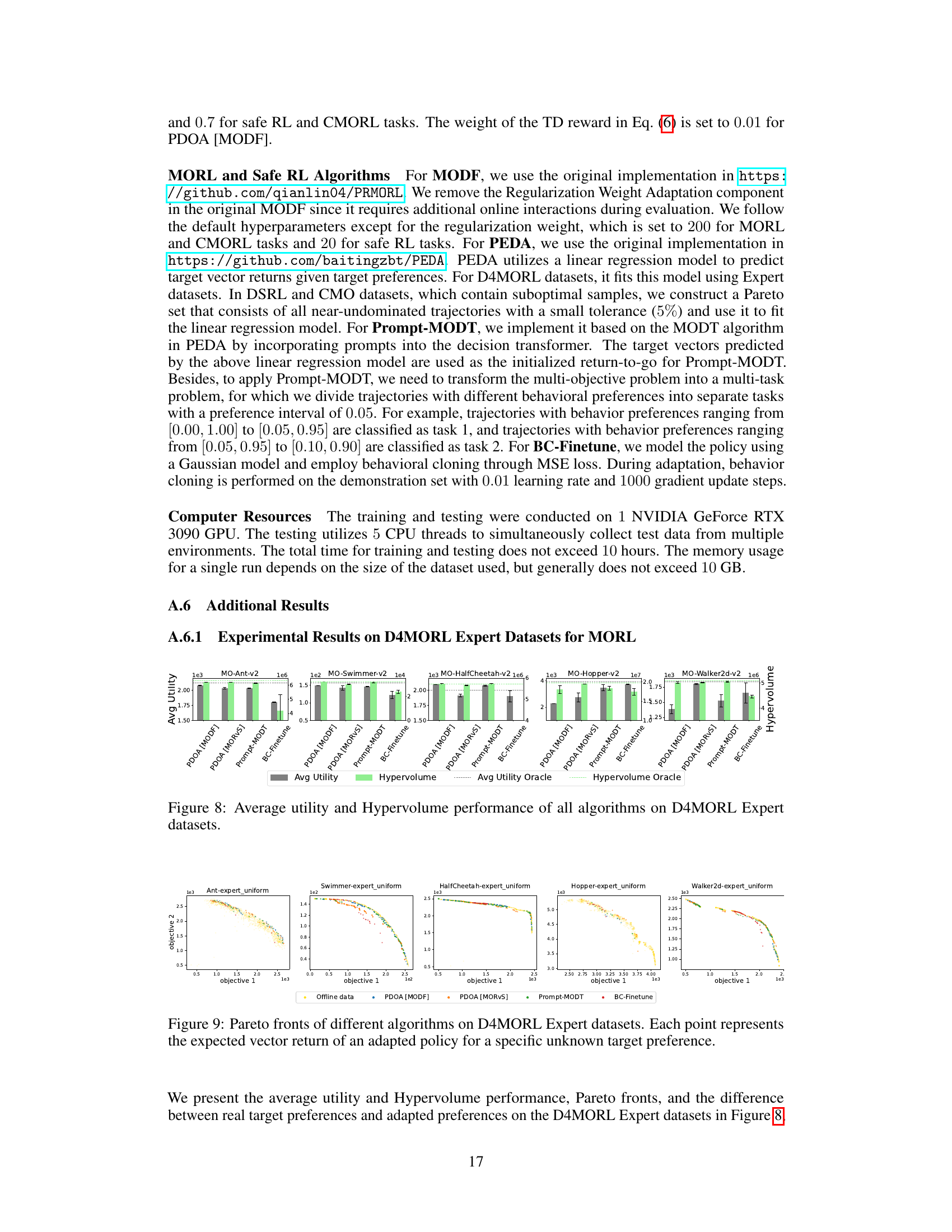
This figure presents the average utility and hypervolume achieved by different algorithms on the D4MORL Expert datasets. The algorithms include PDOA using MODF and MORVS, Prompt-MODT, BC-Finetune, and the oracle performance (original MODF and MORVS). The results are shown for five different MuJoCo tasks: Ant, Swimmer, HalfCheetah, Hopper, and Walker2d. Each bar represents the average performance across multiple runs, and error bars indicate the standard deviation. The dashed lines represent the oracle performance, serving as the best achievable results given full knowledge of the preferences.

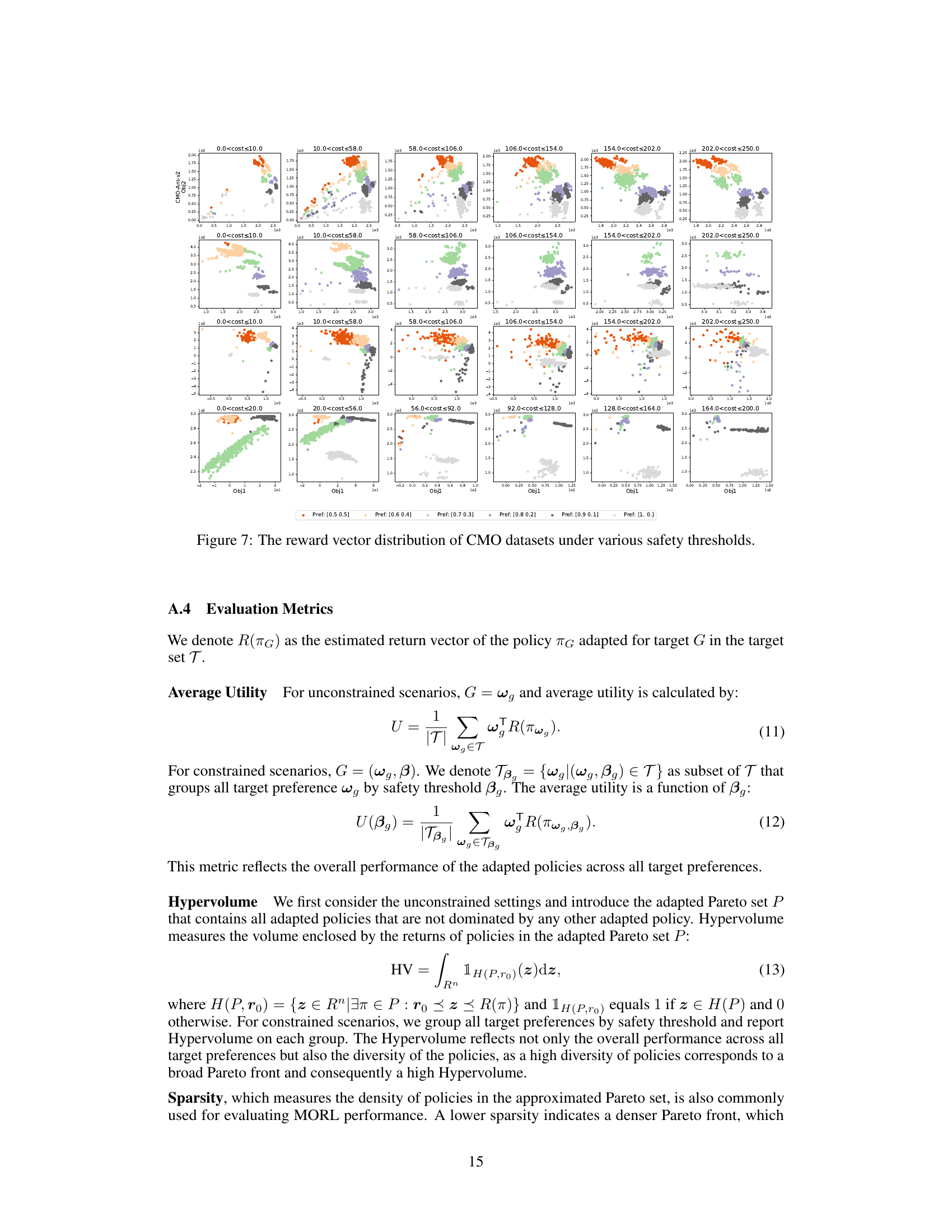
This table provides detailed information about the different Constrained Multi-Objective Reinforcement Learning (CMORL) tasks used in the paper’s experiments. It shows the behavioral preference set, cost function (velocity constraint), threshold range for the velocity constraint, and the objectives of each task (a combination of speed, jumping height, and energy consumption). This information is crucial for understanding the experimental setup and the specific challenges each task presents.
In-depth insights#
Offline MORL Adapt#
Offline multi-objective reinforcement learning (MORL) adaptation presents a significant challenge. Existing MORL methods typically rely on pre-defined preferences, often requiring extensive human effort to specify. An offline adaptation framework is highly desirable as it would allow leveraging existing datasets without the need for additional online interactions or manual preference tuning. This is particularly relevant in safety-critical applications where online interactions are risky. A successful approach would involve methods to infer preferences implicitly from demonstrations, effectively bridging the gap between available data and desired policy behavior. Key research questions revolve around robust preference estimation from limited demonstrations, efficient adaptation algorithms, and generalization performance across varying environments and objectives. Addressing the challenges of uncertainty, noise in data, and efficient inference methods is critical to the success of offline MORL adaptation. Furthermore, ensuring that the adapted policies comply with constraints, especially safety constraints, is paramount. A well-defined framework should carefully balance exploration and exploitation of available data to ensure performance and safety are maintained.
Constrained MORL#
Constrained Multi-Objective Reinforcement Learning (Constrained MORL) tackles the challenge of optimizing multiple, potentially conflicting objectives while adhering to safety or resource constraints. It extends standard MORL by incorporating limitations, making it more applicable to real-world scenarios. The core difficulty lies in finding policies that achieve a desirable balance between the objectives, represented by a Pareto front, while simultaneously satisfying the constraints. Methods often involve techniques like constraint satisfaction, penalty methods, or Lagrangian formulations, which aim to integrate the constraints into the optimization process. However, determining suitable constraint thresholds and preference weights for objectives can be highly dependent on the problem’s specifics and human expertise. The need for efficient methods to infer these parameters from data, possibly through techniques like offline adaptation using demonstrations, is paramount for the practical use of constrained MORL in diverse application areas, particularly in domains where extensive online experimentation is impractical or risky.
Preference Inference#
Preference inference in multi-objective reinforcement learning (MORL) is crucial because it allows agents to learn optimal policies without explicit human specification of preferences. Inferring preferences directly from demonstrations offers a significant advantage over traditional methods requiring explicit preference weighting, which can be subjective and time-consuming. Several approaches exist: one might learn a mapping from demonstrations to a distribution over preferences, allowing for the selection of a policy that best aligns with the implicit preferences shown in the data. Alternatively, a model could be trained to predict preferences given observations of an agent’s behavior, with techniques like inverse reinforcement learning being applicable here. A key challenge is handling the uncertainty inherent in inferring preferences from limited data. Robustness to noise and outliers in the demonstration data is paramount. The effectiveness of preference inference will depend heavily on the quality and diversity of the demonstrations and the capabilities of the inference model employed. Methods for evaluating and validating the inferred preferences against true, but possibly unknown, preferences are also essential for building trust and ensuring reliable performance.
Empirical Validation#
An Empirical Validation section in a research paper would rigorously test the proposed approach. It should present results from various experiments designed to showcase the model’s capabilities and limitations. Clear visualizations such as graphs and tables are crucial for presenting key performance metrics. The experiments should be carefully designed to address specific research questions, with appropriate baselines for comparison. The choice of evaluation metrics should be justified and clearly linked to the overall goals of the paper. Statistical significance testing is necessary to ensure that observed differences are not merely due to chance, strengthening the validity of the findings. A robust validation would involve testing across diverse datasets, and potentially analyzing the model’s performance under varying conditions or with different parameter settings. Detailed discussion of the results, including both successes and failures, is vital for presenting a complete and objective evaluation. Furthermore, attention should be paid to the reproducibility of the experiments, outlining the specifics of the experimental setup to allow for replication by other researchers. In short, a strong Empirical Validation section is vital for convincing readers of the approach’s efficacy and reliability.
Future Works#
Future research directions stemming from this work could explore several promising avenues. Extending the offline adaptation framework to handle more complex scenarios, such as those with non-linear preferences or high-dimensional state spaces, would significantly broaden its applicability. Investigating the impact of different demonstration selection strategies on the effectiveness of the adaptation process is crucial for optimizing performance. Developing theoretical guarantees for the convergence and sample efficiency of the proposed method is a key next step for building greater confidence in its reliability. Finally, applying the framework to real-world applications in diverse domains such as robotics and autonomous driving will be essential for validating its practicality and identifying potential challenges in complex and safety-critical situations. A thorough analysis of the robustness of the framework to various forms of noise and uncertainty in the offline data would also be valuable for ensuring reliable performance in practice.
More visual insights#
More on figures

This figure compares the performance of several multi-objective reinforcement learning (MORL) algorithms on the D4MORL Amateur datasets. Each point on the Pareto front represents a different policy that has been adapted to a specific, unknown target preference. The Pareto front shows the trade-off between two objectives. A larger and more expansive Pareto front indicates better performance, as it shows that the algorithm can find a wider range of policies that achieve a good balance between the two objectives. The figure suggests that the proposed PDOA method outperforms other baselines in terms of achieving a wider range of policies with better balance between the objectives.

This figure compares the performance of different algorithms (PDOA [MODF], PDOA [MORVS], Prompt-MODT, BC-Finetune) on the D4MORL Amateur datasets across five different multi-objective reinforcement learning tasks. The y-axis represents the average utility and hypervolume, while the x-axis represents the different tasks. Higher values in both metrics indicate better performance. Dashed lines represent the best performance achieved by either MODF or MORVS (original, non-adapted methods) on each task. This figure visually demonstrates the superior performance of the proposed PDOA framework compared to the baselines.
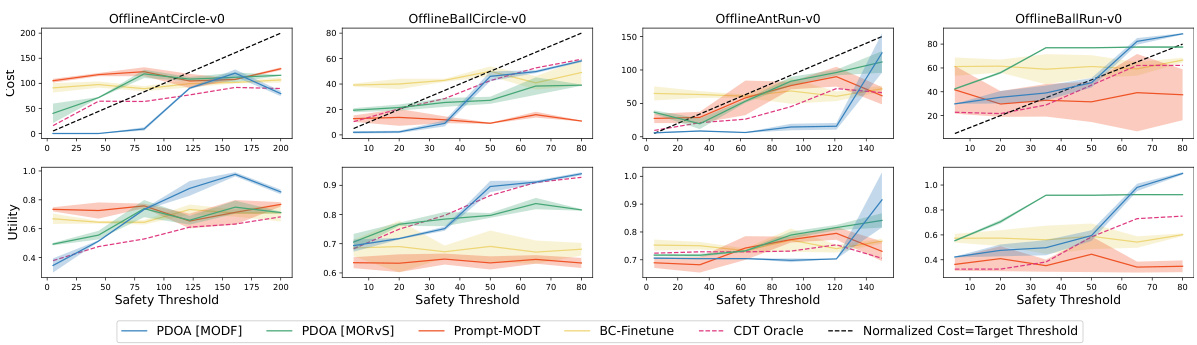
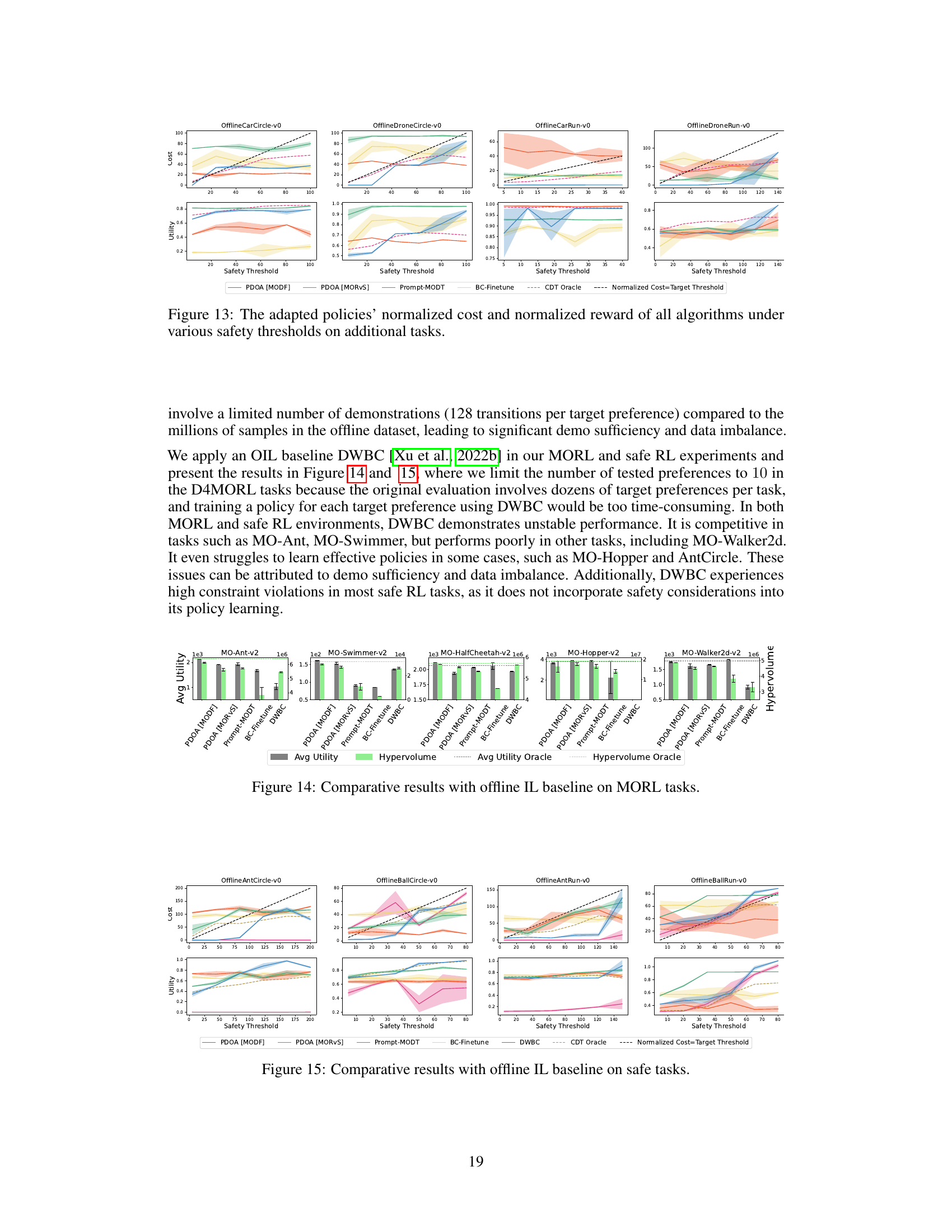
This figure compares the performance of different algorithms on safe RL tasks under various safety thresholds. The x-axis represents the safety threshold, and the y-axis shows both the normalized cost (top row) and utility (bottom row) of the policies generated by each algorithm. The black dashed line indicates the safety threshold; points above this line represent policies that violate the safety constraints. The plot shows how well each algorithm balances utility maximization with constraint satisfaction across different safety thresholds. The algorithms compared include PDOA (using MODF and MORVS), Prompt-MODT, BC-Finetune, and CDT (an oracle baseline that knows the thresholds).
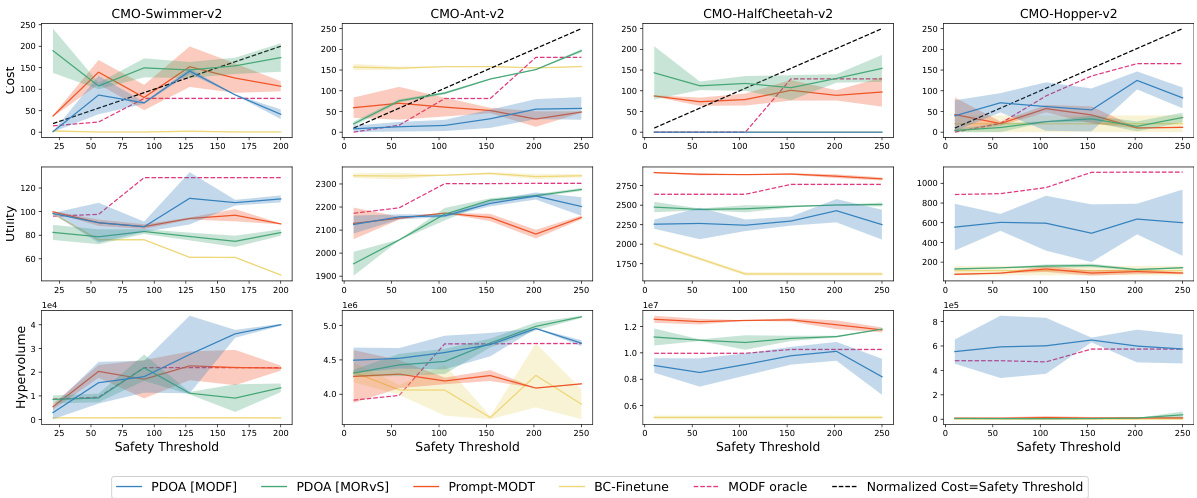
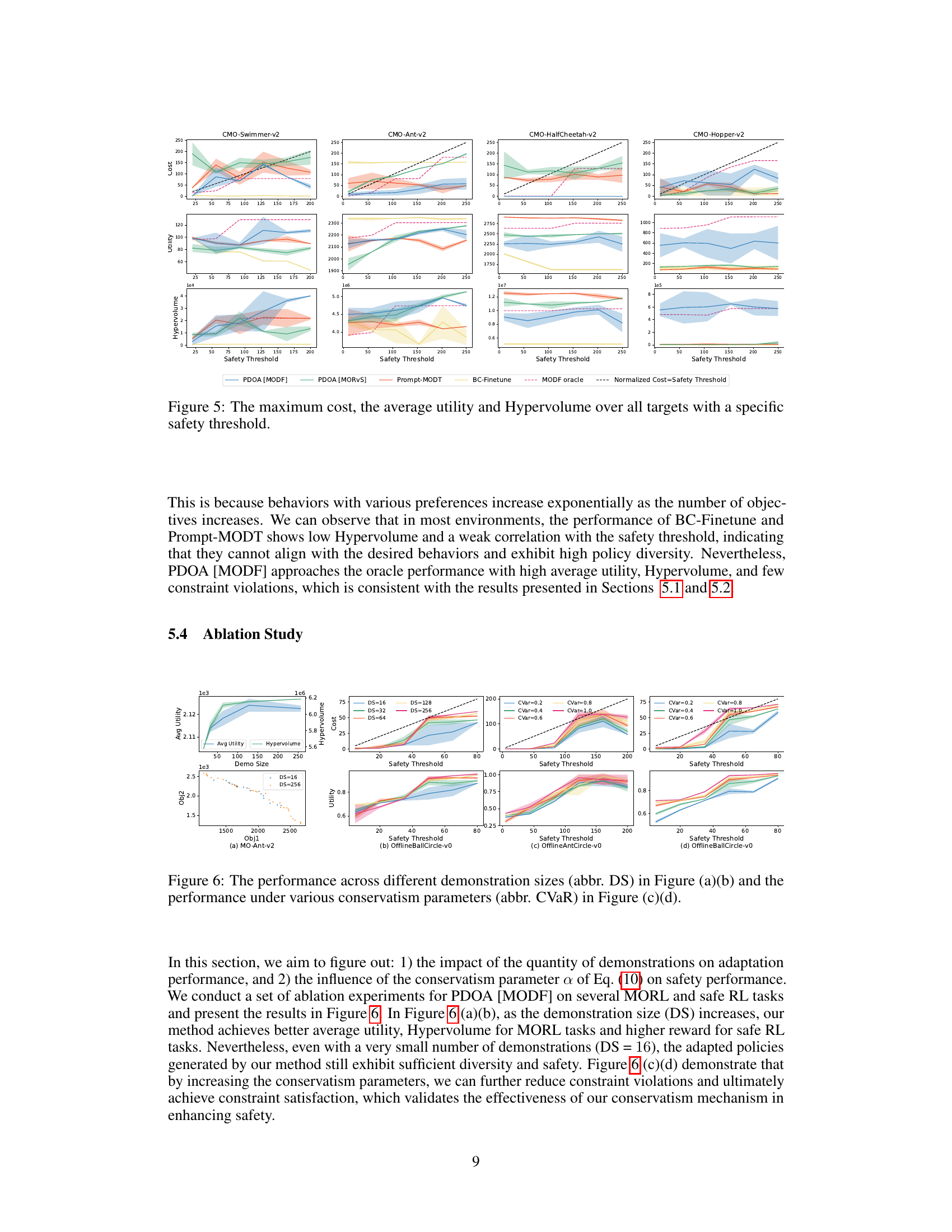
This figure shows the performance of different algorithms on constrained multi-objective reinforcement learning tasks. Specifically, it presents the maximum cost incurred, the average utility achieved, and the hypervolume covered by the Pareto front for various safety thresholds. The results illustrate the ability of the proposed PDOA framework to maintain a balance between maximizing utility and satisfying safety constraints, particularly when comparing it to baselines that do not consider safety during training.
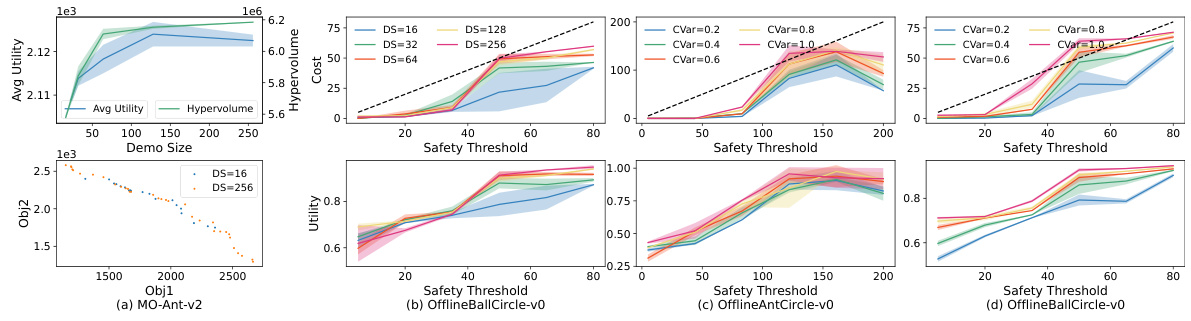
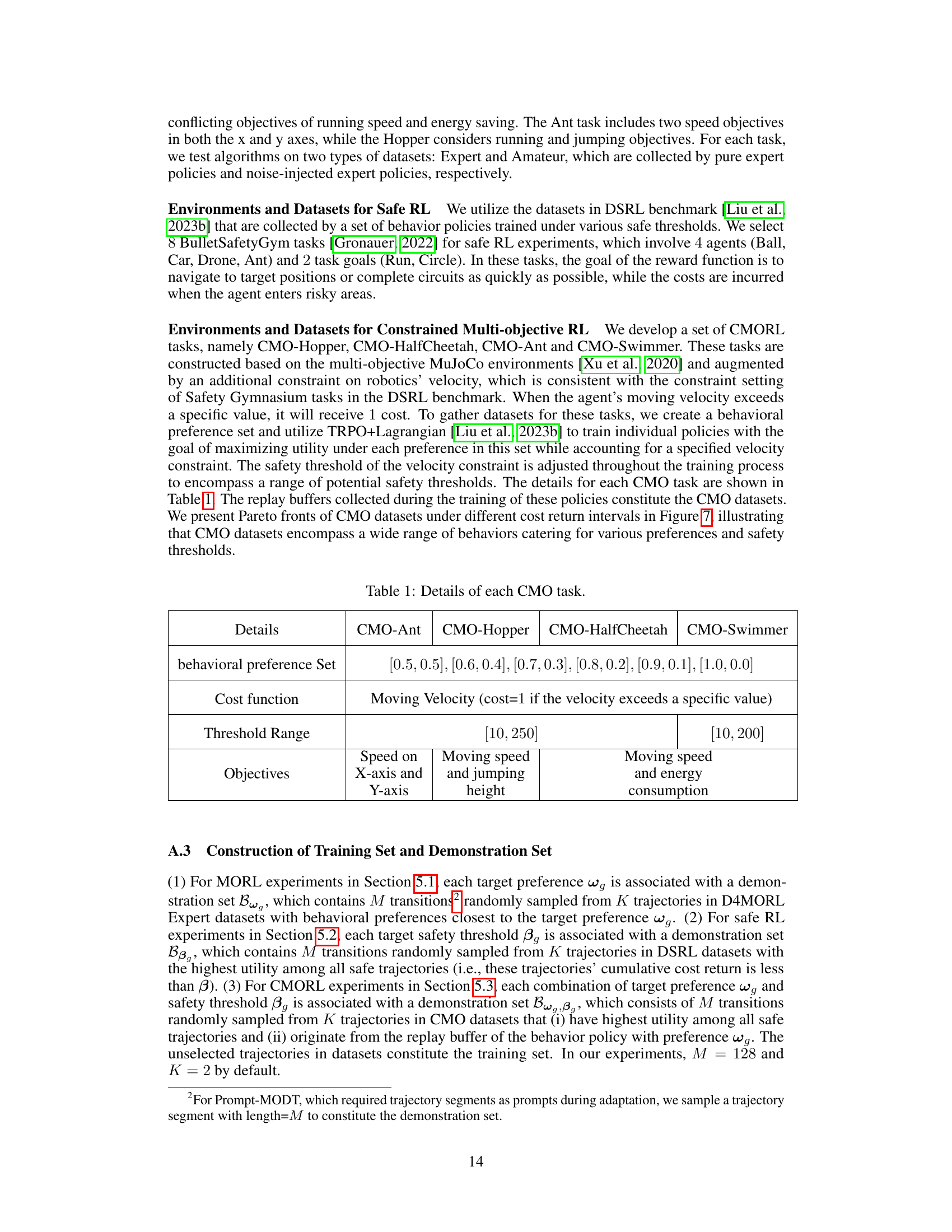
This figure presents ablation study results on the impact of demonstration size and conservatism parameter on the performance of PDOA[MODF]. Figures (a) and (b) show that increasing the demonstration size leads to better average utility and hypervolume in MORL tasks and higher reward in safe RL tasks. Even with small demonstration sizes, the method shows sufficient diversity and safety. Figures (c) and (d) demonstrate that increasing the conservatism parameter reduces constraint violations and improves safety, validating the conservatism mechanism.

This figure shows the reward vector distributions for six different constrained multi-objective reinforcement learning (CMORL) tasks under different safety thresholds. Each subfigure represents a specific task and cost range. The x and y axes show the rewards for two objectives, while the points are colored according to the behavioral preference used to generate the data. The figure illustrates how the reward distributions change with different cost constraints and preferences.

This figure presents the results of five different algorithms (PDOA [MODF], PDOA [MORVS], Prompt-MODT, BC-Finetune, and the oracle performance from MODF and MORVS) on five multi-objective reinforcement learning tasks from the D4MORL Amateur dataset. The performance is measured by two metrics: Average Utility and Hypervolume. Higher values for both metrics indicate better performance. The dashed lines show the best performance achieved by the original MODF and MORVS algorithms, serving as a benchmark against which the other algorithms are compared.

This figure compares the performance of different algorithms in multi-objective reinforcement learning using the D4MORL Expert dataset. Each point on the Pareto front represents a different policy adapted to a specific, unknown target preference. The algorithms compared include PDOA (using MODF and MORVS), Prompt-MODT, and BC-Finetune. The figure helps visualize how well each algorithm balances multiple objectives and achieves diversity in the resulting policies.

This figure compares the real target preferences against the adapted preferences obtained using the PDOA (Preference Distribution Offline Adaptation) framework on the D4MORL Expert datasets. Each subplot represents a different MuJoCo task (Ant, Swimmer, HalfCheetah, Hopper, Walker2d). The x-axis shows the real target preference on objective 1, while the y-axis displays the adapted preference on objective 1, as estimated by the PDOA method. The lines represent the results using two different offline MORL algorithms (MODF and MORvS) within the PDOA framework. The diagonal dashed line indicates a perfect match between real and adapted preferences. Deviations from this line illustrate the accuracy of the PDOA method in aligning adapted preferences with the ground truth.

This figure displays the performance of the PDOA framework on four different safe RL tasks. For each task, the x-axis represents the normalized cost, while the y-axis represents the normalized reward. Each point represents a policy generated by the PDOA [MODF] and PDOA [MORVS] algorithms, with different preferences. The plot shows the relationship between the cost and reward for policies with varying preferences, demonstrating the capability of the framework to generate policies that achieve different trade-offs between cost and reward while satisfying the constraints.

This figure compares the performance of several algorithms (PDOA[MODF], PDOA[MORVS], Prompt-MODT, BC-Finetune, and CDT Oracle) on four additional safe reinforcement learning tasks (OfflineCarCircle-v0, OfflineDroneCircle-v0, OfflineCarRun-v0, OfflineDroneRun-v0) under different safety thresholds. The plot shows the normalized cost versus normalized reward for each algorithm and threshold. It illustrates the trade-off between safety (low cost) and performance (high reward). The goal is to find policies that satisfy the safety constraints while maximizing reward.

This figure compares the performance of different algorithms (PDOA [MODF], PDOA [MORvS], Prompt-MODT, BC-Finetune, and CDT Oracle) on four different safe RL tasks (OfflineAntCircle-v0, OfflineBallCircle-v0, OfflineAntRun-v0, and OfflineBallRun-v0) across various safety thresholds. The x-axis represents the safety threshold, while the y-axis shows both the normalized cost (top row) and normalized utility (bottom row) achieved by the algorithms’ resulting policies. The black dashed line indicates the threshold where policies violate the constraints. The figure illustrates the ability of the PDOA algorithms to effectively meet the safety constraints while maintaining a reasonable level of utility, outperforming the other algorithms, especially at tighter safety thresholds.
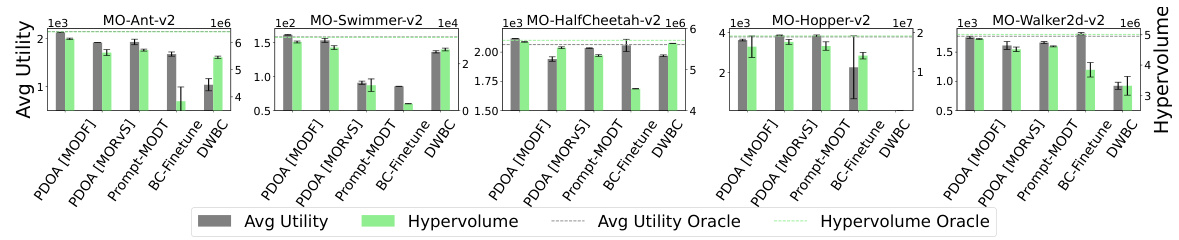
This figure compares the performance of different algorithms (PDOA [MODF], PDOA [MORVS], Prompt-MODT, BC-Finetune, and DWBC) on the D4MORL Expert datasets across five multi-objective tasks: MO-Ant-v2, MO-Swimmer-v2, MO-HalfCheetah-v2, MO-Hopper-v2, and MO-Walker2d-v2. For each task, two metrics are shown: Average Utility and Hypervolume, both representing different aspects of the algorithms’ performance in balancing multiple objectives. The dashed lines represent the best performance achievable with full knowledge of the true target preferences (oracle performance). The results show the effectiveness of the proposed PDOA framework compared to existing baseline approaches.

This figure presents the performance of several algorithms on safe reinforcement learning tasks with safety constraints. The x-axis represents the safety threshold, while the y-axes represent the normalized cost and utility (reward) of the learned policies. Each point represents the performance of a policy trained using a particular method. The black dashed line indicates the safety threshold that must not be violated. Policies with costs exceeding the threshold are shown above the line. The figure helps to assess the ability of different methods in meeting safety constraints while maximizing reward.

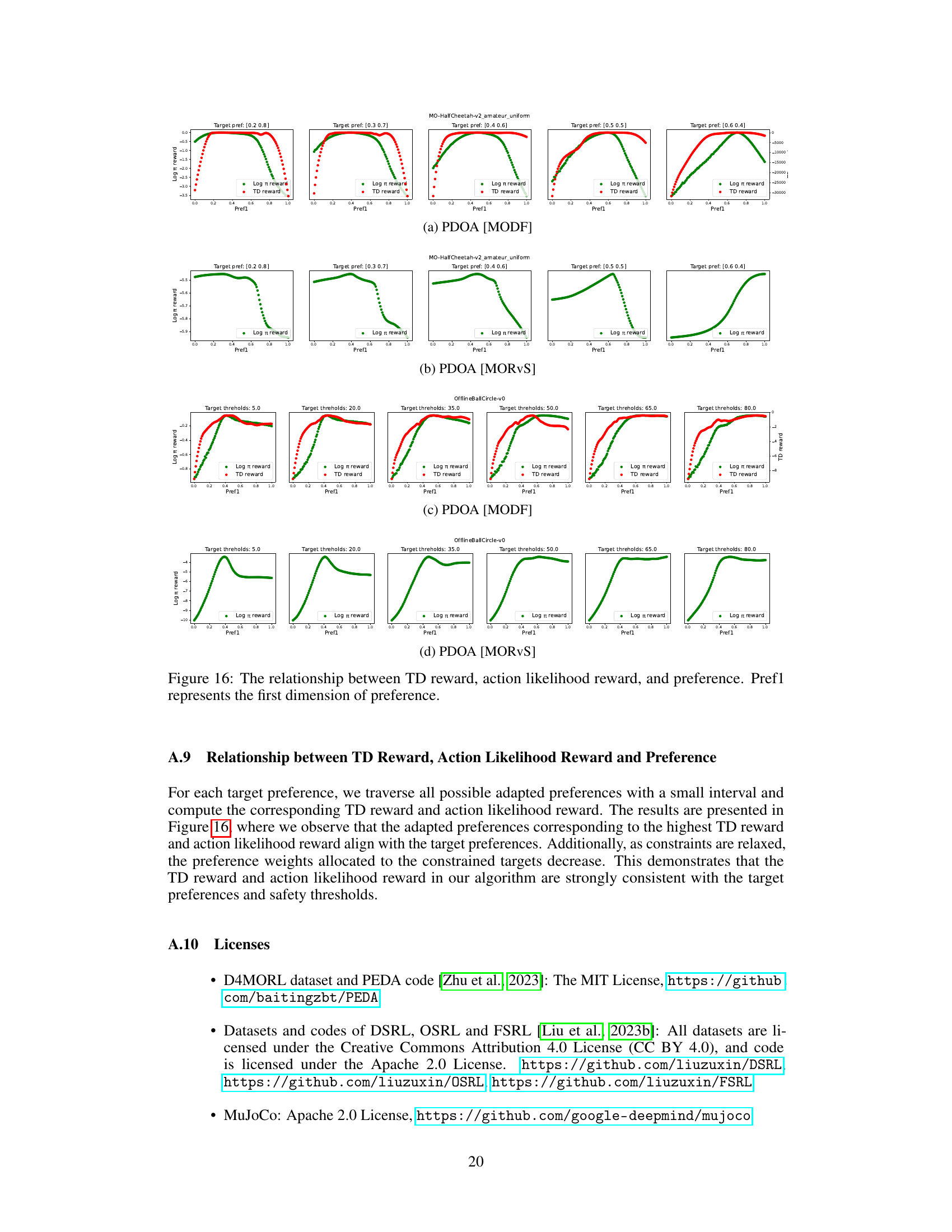
This figure visualizes the relationship between TD reward, action likelihood reward, and preference for both PDOA[MODF] and PDOA[MORVS]. It shows the correlation between these factors and the target preferences across various tasks (MO-HalfCheetah and OfflineBallCircle). The plots illustrate how the TD and action likelihood rewards vary with the first dimension of preference (Pref1), providing insights into how the algorithm identifies the target preference.
Full paper#