↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large Language Models (LLMs) surprisingly exhibit Chain-of-Thought (CoT) reasoning, solving complex problems by generating intermediate reasoning steps. However, the underlying mechanisms remain unclear. This limits our ability to design more effective and interpretable LLMs. Existing research offers limited understanding of CoT’s inner workings and conditions for its appearance.
This research investigates how CoT reasoning emerges in transformers through controlled experiments. The study introduces iterative tasks and algorithms to analyze the emergence of CoT in a simplified setting. By examining attention patterns within a two-layer transformer, researchers identified a specialized attention mechanism, named “iteration heads,” that facilitates CoT. The study demonstrates how iteration heads enable the transformer to solve iterative problems effectively, highlighting the importance of attention mechanisms in enabling more complex reasoning. The findings reveal that iteration heads exhibit good transferability between tasks, showcasing the value of data curation strategies for improving LLM performance.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a mechanistic explanation for the emergence of Chain-of-Thought (CoT) reasoning in large language models (LLMs). By using controlled experiments and interpretable architectures, the research sheds light on how CoT capabilities arise, which is vital for improving LLM design and understanding their reasoning processes. This understanding is critical for advancing AI safety and building more robust and reliable AI systems. The findings also open new avenues for researching data curation techniques to enhance LLM performance.
Visual Insights#

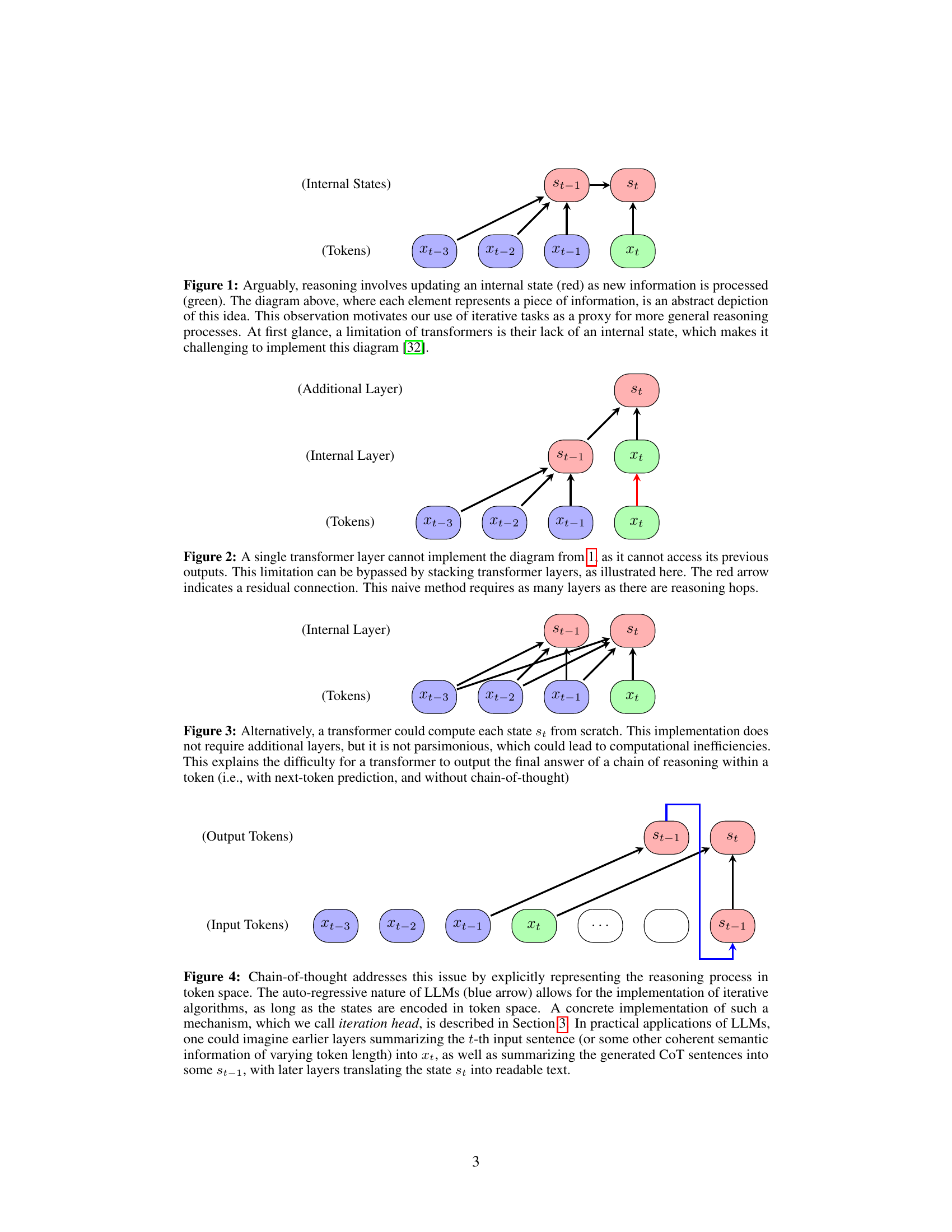
This figure illustrates the concept of reasoning as an iterative process of updating an internal state based on incoming information. Each node represents a piece of information, with green nodes representing new information and the red node representing the internal state. The arrows show how the internal state is updated with each new piece of information. The figure highlights the challenge of implementing this type of iterative reasoning in transformers, which typically lack an explicit internal state mechanism.

This table shows the difference between a single-token prediction and a chain-of-thought prediction. In single-token prediction, the model directly answers the question with one token. In chain-of-thought prediction, the model first generates reasoning steps before giving the final answer. This illustrates how chain-of-thought improves the quality of answers generated by large language models, even when they are not explicitly trained for reasoning tasks. The example question is ‘What is 8 × 8 × 3?’
In-depth insights#
CoT Emergence#
The emergence of Chain-of-Thought (CoT) reasoning in large language models (LLMs) is a fascinating area of research. While LLMs are initially trained on next-token prediction tasks, they surprisingly exhibit the ability to perform complex reasoning when prompted appropriately. This phenomenon is not explicitly programmed but rather emerges from the intricate interplay of model architecture and training data. The paper highlights the role of specialized attention mechanisms, referred to as ‘iteration heads’, in enabling CoT reasoning. These iteration heads appear to facilitate iterative processing by enabling the model to maintain and update an internal state as it progresses through the reasoning steps. The emergence of these iteration heads seems to be influenced by the training data, with iterative tasks leading to their development. Crucially, these skills exhibit transferability, demonstrating that the CoT capabilities acquired through training on one type of iterative task can generalize to others. This observation suggests a modularity to CoT reasoning, implying that specific components (such as iteration heads) can be applied across various reasoning problems. This mechanistic understanding of CoT emergence is crucial for advancing the development of more capable and interpretable LLMs.
Iteration Heads#
The concept of “Iteration Heads” in the context of the provided research paper offers a novel mechanistic interpretation of Chain-of-Thought (CoT) reasoning in transformer models. It posits that specialized attention mechanisms, termed “iteration heads,” emerge within the transformer’s architecture to facilitate iterative reasoning processes. These heads are not explicitly programmed but rather self-organize during training on sufficiently complex iterative tasks. The research indicates that these iteration heads exhibit a specific pattern of weights that allow for the efficient tracking and updating of internal states throughout the iterative process. This mechanistic understanding of CoT reasoning provides crucial insights into how transformers learn to solve complex problems by breaking them down into manageable steps. The study highlights the transferability of the learned CoT skills across different iterative tasks, suggesting a potential for generalization and efficient learning. Further research into iteration heads could significantly advance the development of more robust and efficient reasoning capabilities in large language models.
Iterative Tasks#
The concept of “Iterative Tasks” in the context of this research paper centers on problems solvable through iterative algorithms. These tasks are designed to be challenging for standard transformer models using single-token prediction, because they necessitate the accumulation of information and state over multiple steps. The paper cleverly leverages iterative tasks to demonstrate how Chain-of-Thought (CoT) reasoning emerges in transformers. Simple yet revealing iterative tasks, like copying sequences, polynomial iterations, and parity checks, highlight the limitations of single-token prediction while showcasing the efficacy of CoT. These controlled experiments allow for in-depth analysis of attention mechanisms, revealing the development of specialized “iteration heads” crucial to the success of CoT reasoning. The focus on iterative tasks provides a mechanistic lens into CoT and facilitates understanding of how transformers learn multi-step reasoning processes.
Transferability#
The concept of transferability in the context of Chain-of-Thought (CoT) reasoning within large language models (LLMs) is crucial. It examines whether CoT abilities learned on a specific task generalize to other, seemingly unrelated tasks. Positive transferability suggests that training on a simple iterative task, like copying or parity problems, enhances performance on more complex iterative problems, showcasing the emergence of a generalizable reasoning mechanism. This implies that LLMs might develop internal “circuits” dedicated to multistep reasoning, transferable across different tasks with similar underlying logical structures. Negative transferability, however, highlights the limitations of this generalization. The extent of transfer is highly dependent on factors like task similarity, model architecture, and training data characteristics. The degree of similarity in the underlying computational processes dictates the success of transfer. Investigating transferability is vital for understanding CoT’s true potential and improving LLM efficiency and robustness. Future research should explore the boundaries of this transfer, focusing on developing methods for predicting which skills will transfer and quantifying the extent of that transfer.
Ablation Studies#
Ablation studies systematically remove components of a model or system to assess their individual contributions. In the context of this research paper, ablation studies likely involved removing or altering aspects of the transformer architecture, such as attention mechanisms, layers, or specific weight distributions, to evaluate their impact on the model’s capacity to perform iterative reasoning tasks. The results of these studies are crucial to understanding the mechanistic underpinnings of chain-of-thought reasoning. They help determine whether certain components are essential to CoT capabilities or if the model’s success depends on a combination of factors. By demonstrating the importance of specific architectural elements, such as the hypothesized ‘iteration heads’, ablation studies provide strong evidence for the proposed mechanisms and refine our understanding of how these models work. The transferability of CoT skills observed across various tasks and the effect of hyperparameters further strengthens the insights gained, illuminating the key elements for effective iterative reasoning.
More visual insights#
More on figures
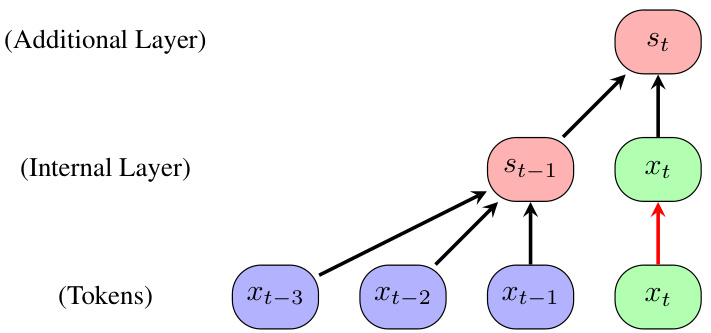
This figure illustrates how a single transformer layer cannot maintain an internal state across multiple reasoning steps because it lacks access to previous outputs. The diagram shows that to implement the iterative reasoning process, multiple layers are needed. Each layer processes the current input token and the previous internal state (residual connection) to generate the next internal state. This approach, however, is inefficient as it needs a number of layers equal to the number of reasoning steps required.
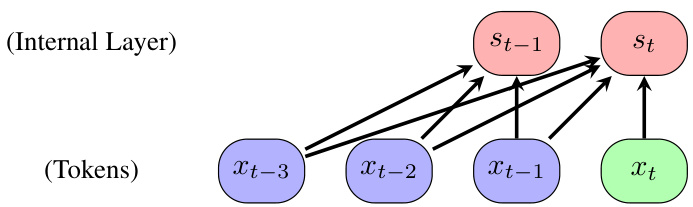
This figure shows a diagram illustrating how reasoning involves updating an internal state as new information is processed. Each element in the diagram represents a piece of information. The figure highlights that transformers lack an internal state, making it challenging to directly implement the diagram’s concept.
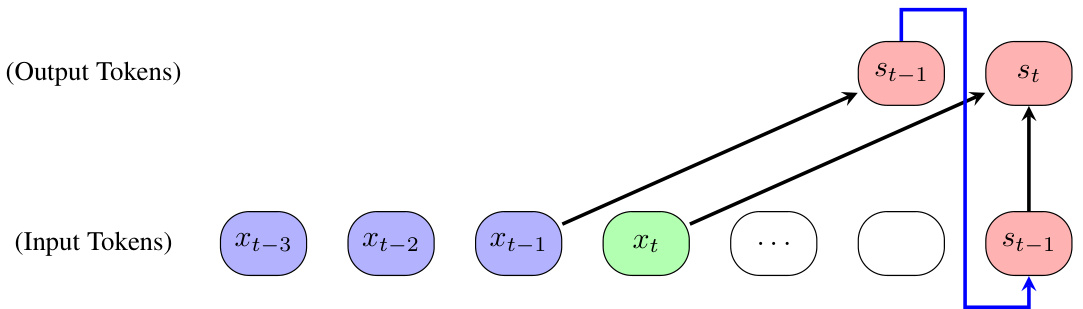
This figure illustrates how chain-of-thought reasoning allows transformers to solve iterative tasks. It shows that by explicitly representing the reasoning steps as tokens, the autoregressive nature of LLMs can be leveraged to implement iterative algorithms. The figure highlights the key concept of an ‘iteration head’, a mechanism that enables the transformer to maintain and update an internal state (st) across multiple reasoning steps, eventually leading to a final answer. The internal states are represented as tokens, enabling iterative processing within the transformer’s autoregressive framework. The diagram contrasts this approach with the limitations of single-token prediction, illustrating the benefits of CoT reasoning for handling iterative tasks.
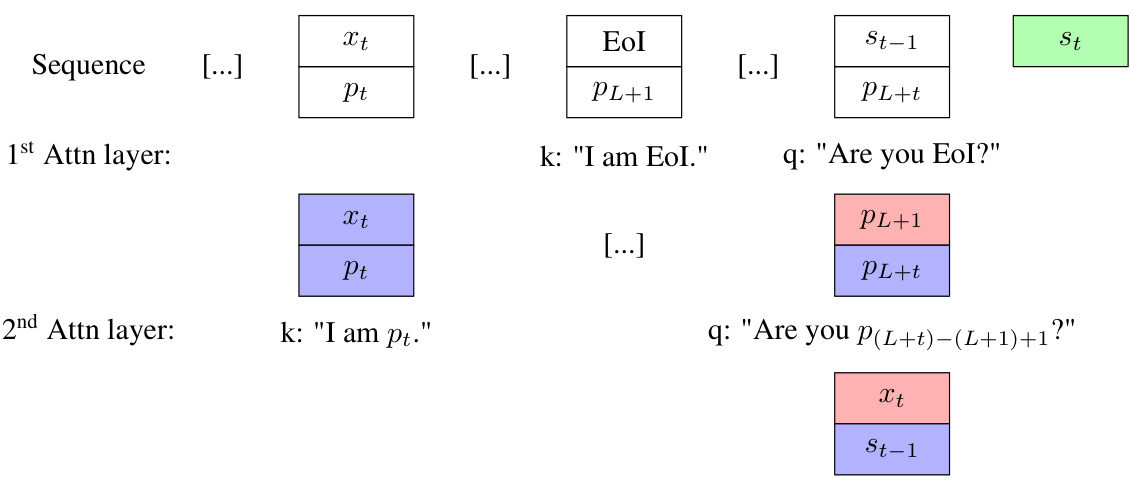
This figure illustrates how a two-layer transformer can implement an iterative algorithm using an ‘iteration head.’ The first layer uses attention to identify the end-of-input token and retrieves the position of the current token. The second layer uses attention to retrieve both the previous state (st-1) and current token (xt) which allows the MLP to calculate the next state (st). This demonstrates how the transformer can effectively perform iterative reasoning.

The figure displays attention maps and accuracy dynamics when training a transformer on the parity problem. The left side shows that the first attention layer focuses on identifying the end-of-input token, while the second attention layer focuses on extracting relevant tokens for iterative processing. The right side illustrates how the model’s accuracy on this task increases with the number of training epochs, particularly for shorter sequences, showcasing a characteristic pattern of stepwise improvements.
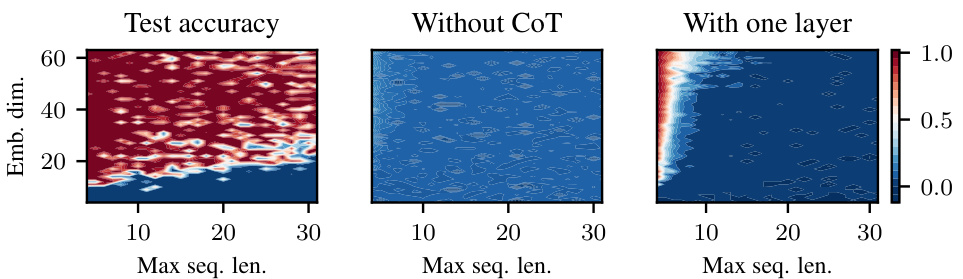
This figure compares the test accuracy of three different model setups when learning the polynomial iteration task. The x-axis shows the maximum sequence length, and the y-axis shows the embedding dimension. The leftmost plot shows a two-layer transformer using chain-of-thought (CoT), the middle plot shows a two-layer transformer without CoT, and the rightmost plot shows a one-layer transformer with CoT. Redder colors indicate better performance. The figure demonstrates that using CoT with a two-layer transformer leads to significantly better performance than the other methods.

The figure shows the attention maps learned by a transformer when solving the parity problem. The left panel shows the attention weights for the first and second layers. The yellow lines highlight how the model focuses on the end-of-input (EoI) token in the first layer and on the current token in the second layer to perform iterative reasoning. The right panel illustrates the accuracy of the model during training as a function of the sequence length, showing fast learning for shorter sequences and slower learning for longer sequences.
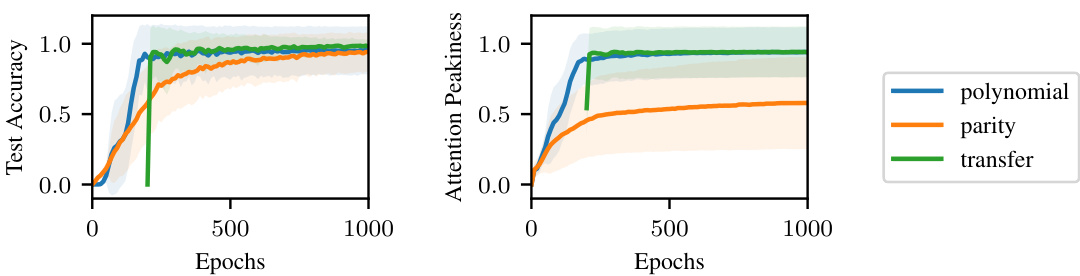
This figure compares the learning curves of three scenarios: learning the polynomial iteration task, learning the parity problem, and learning the parity problem after pre-training on the polynomial iteration task. The left panel shows the test accuracy over epochs, while the right panel shows the attention peakiness score, indicating whether the network learns the iteration head. The green curve demonstrates the benefit of transfer learning, where pre-training on a related task improves learning efficiency for the target task.
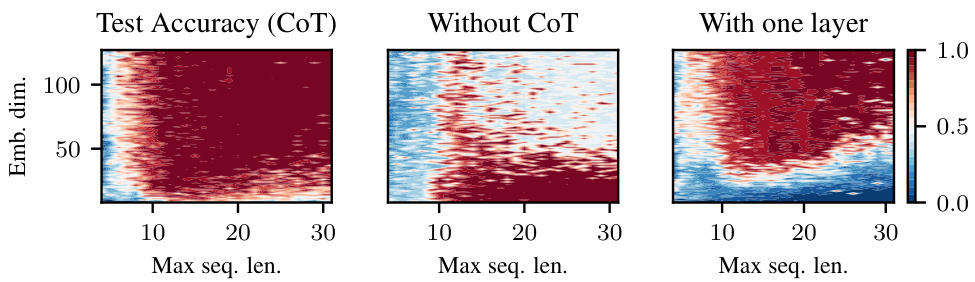
This figure shows the test accuracy of a two-layer transformer trained on the polynomial iteration task, comparing three different training scenarios: with chain-of-thought (CoT), without CoT, and with CoT using only one layer. The accuracy is shown as a heatmap across different embedding dimensions and maximum sequence lengths. Red indicates better performance. The figure highlights the superior performance of the two-layer transformer with CoT, demonstrating the usefulness of this approach for solving iterative tasks.

The figure shows the results of an experiment to learn the polynomial iteration task. The left panel displays a heatmap showing the ‘peakiness’ score (a measure of how concentrated the attention is) for the first and second attention layers as a function of embedding dimension and maximum sequence length. The right panel shows examples of attention maps that illustrate an alternative circuit learned by the model, where attention is not focused on all positions but rather subsampled, especially in lower embedding dimensions.

This figure shows a comparison of the test accuracy achieved using SGD and Adam optimizers across various learning rates and batch sizes. The contour plots illustrate the performance of each optimizer under different hyperparameter settings. Redder colors indicate higher accuracy. The plot helps to visualize the optimal regions in the hyperparameter space for each optimizer, highlighting the effects of learning rate and batch size on model performance.

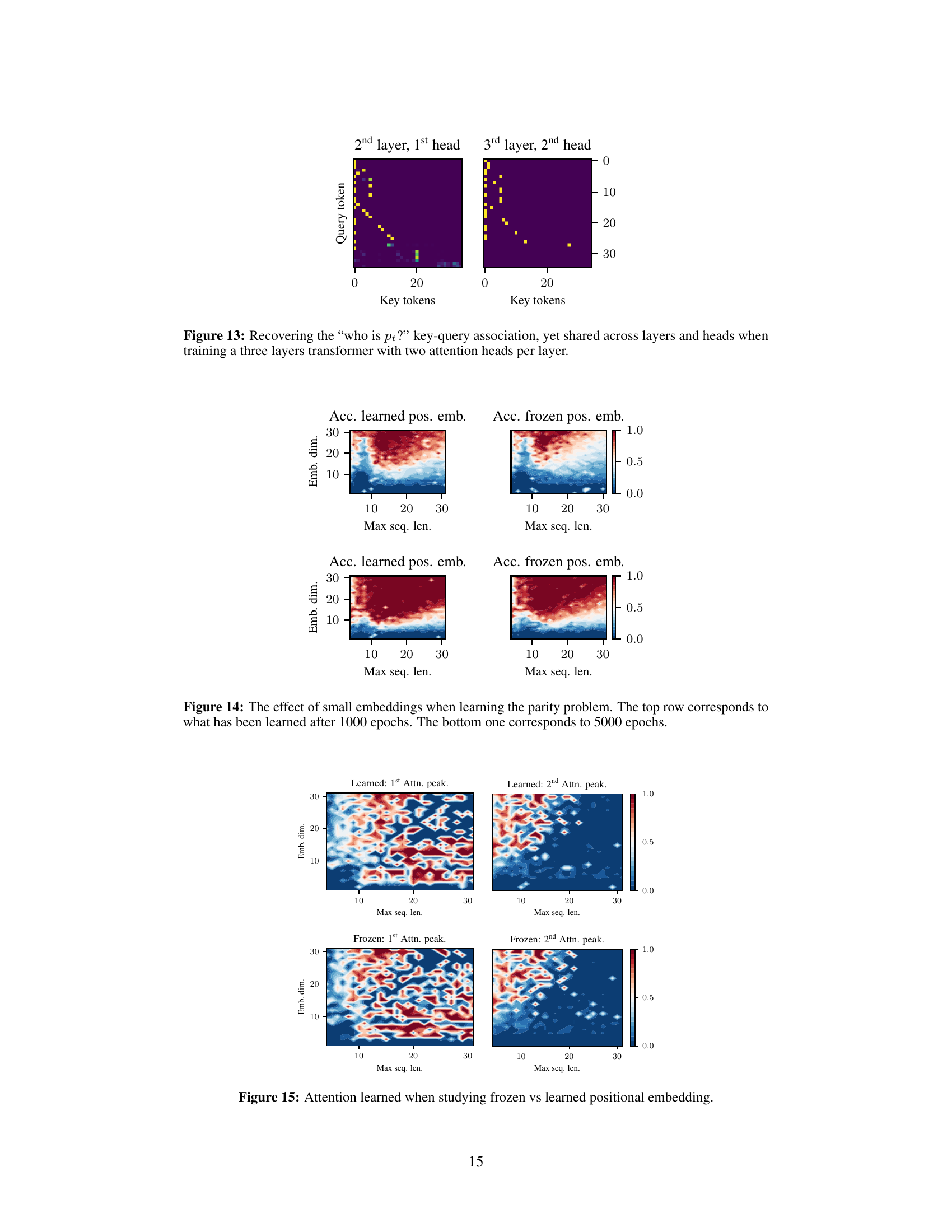
The figure shows the attention maps for a three-layer transformer with two attention heads per layer when trained on an iterative task. It demonstrates that the ‘who is pt?’ key-query association, crucial for iterative reasoning, is not confined to a single layer or head, but rather distributed across multiple layers and heads. This suggests a more complex and robust mechanism for iterative reasoning in larger transformer models than initially hypothesized.

This figure shows the effect of small embedding dimensions on the learning of the parity problem. It presents heatmaps displaying the test accuracy as a function of embedding dimension and maximum sequence length, separately for learned and frozen positional embeddings. The top row shows results after 1000 training epochs, while the bottom row shows results after 5000 epochs. The differences between the two rows highlight how the model’s performance evolves over time and how its capacity to handle longer sequences increases with training.

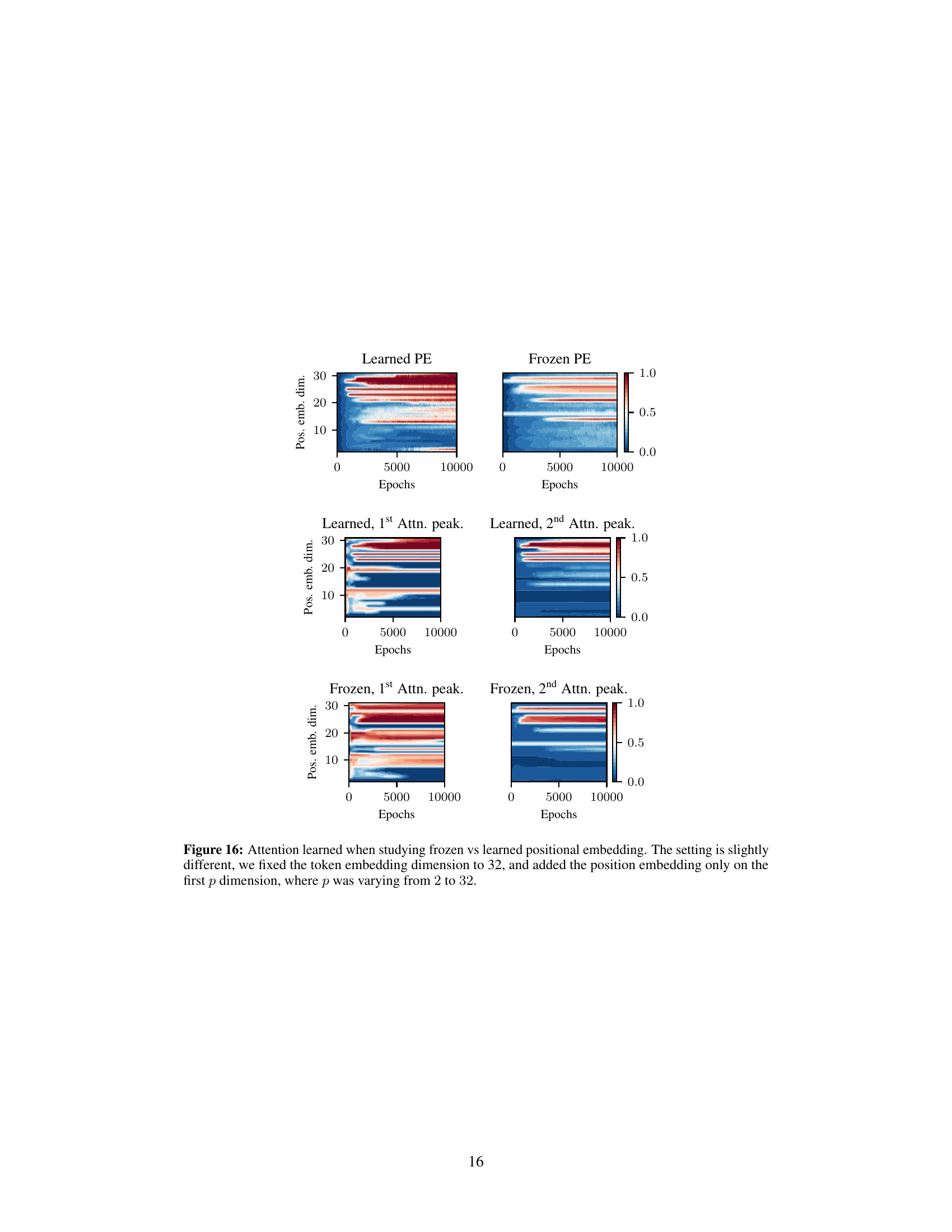
This figure compares the attention peakiness scores (a measure of how closely the attention maps follow the patterns of Figure 6) for both learned and frozen positional embeddings. The top row shows the results when the positional embeddings are learned, while the bottom row shows the results when they are frozen. The left column shows the results for the first attention head, while the right column shows the results for the second attention head. The x-axis represents the maximum sequence length, and the y-axis represents the embedding dimension. The color scale represents the attention peakiness score, with higher values indicating greater concentration of attention. This figure helps to illustrate the effect of learned positional embeddings on the attention mechanism of the transformer model and their contribution to the emergence of iteration heads.
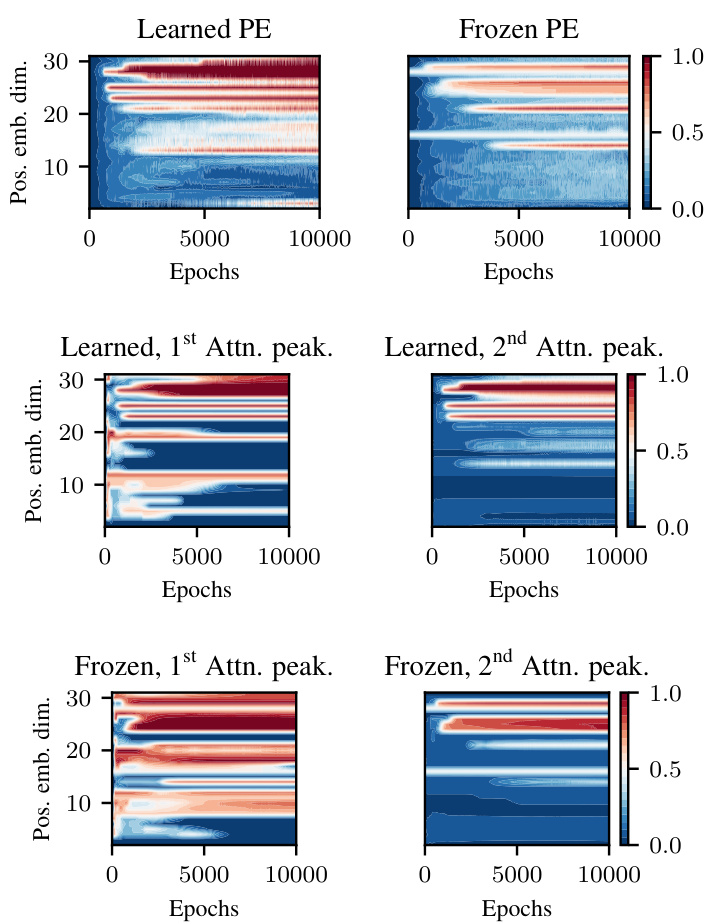
This figure displays the results of an experiment comparing learned and frozen positional embeddings in a transformer model. The experiment focused on learning the parity problem using a model with a token embedding dimension of 32. The positional embeddings were added only to the first p dimensions, with p ranging from 2 to 32. The figure shows the attention peakiness scores (measuring how concentrated the attention is) for both learned and frozen positional embeddings, broken down by the first and second attention heads, and plotted against the maximum sequence length and number of epochs. This helps understand the impact of positional embeddings on learning iteration heads and solving the parity problem.
Full paper#