TL;DR#
The paper tackles a critical problem in differential privacy: comparing continuous distributions while preserving data privacy. Existing methods struggle with continuous data due to the infinite number of possible values and the sensitivity of discretization. This makes it challenging to ensure that a single data change doesn’t drastically affect the outcome, violating the core principles of differential privacy.
The authors introduce a novel algorithm that cleverly handles these challenges. Instead of repeatedly discretizing the data, it uses a technique involving randomly setting discretization points with noise, limiting the impact of individual data points on the result. This technique, along with a carefully designed privacy analysis and utility analysis, allows the algorithm to accurately assess whether two continuous distributions are similar or significantly different while guaranteeing differential privacy. The research opens up exciting possibilities for privacy-preserving data analysis in various fields that rely on continuous data.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and hypothesis testing. It bridges a significant gap in the field by tackling the challenging problem of equivalence testing for continuous distributions, opening new avenues for privacy-preserving data analysis in various domains dealing with sensitive continuous data such as health, finance, and economics. The proposed algorithm and its analysis offer valuable insights and techniques that can be adapted and extended to other privacy-related problems.
Visual Insights#

🔼 This figure illustrates how two neighboring datasets (S and S’) differing by a single data point affect the binning process used in the algorithm. The addition of Bernoulli random variables to the bin indices (π₁, π₂ etc.) is highlighted, showing how this helps correlate the bins even with the addition or removal of a single data point. It demonstrates the algorithm’s robustness to changes in the datasets. The top row shows the sorted data for dataset S, and the bottom row is for dataset S’. The figure depicts a situation where a change occurs at the beginning of the sorted data in one dataset but at the end in the other, to illustrate how it affects the bins defined by using the added Bernoulli random variables.
read the caption
Figure 1: Two neighboring inputs that differ on one datapoint, appearing first in S and last in S'. In this example, the index defining the first bin, π₁, is such that for S we go B₁ = 0 and for S' we have B₁ = 0; but the index defining the 2nd bin, π2 it does hold that B2 = 0, B2 = 1 so the indices starting from bin 2 onwards align.

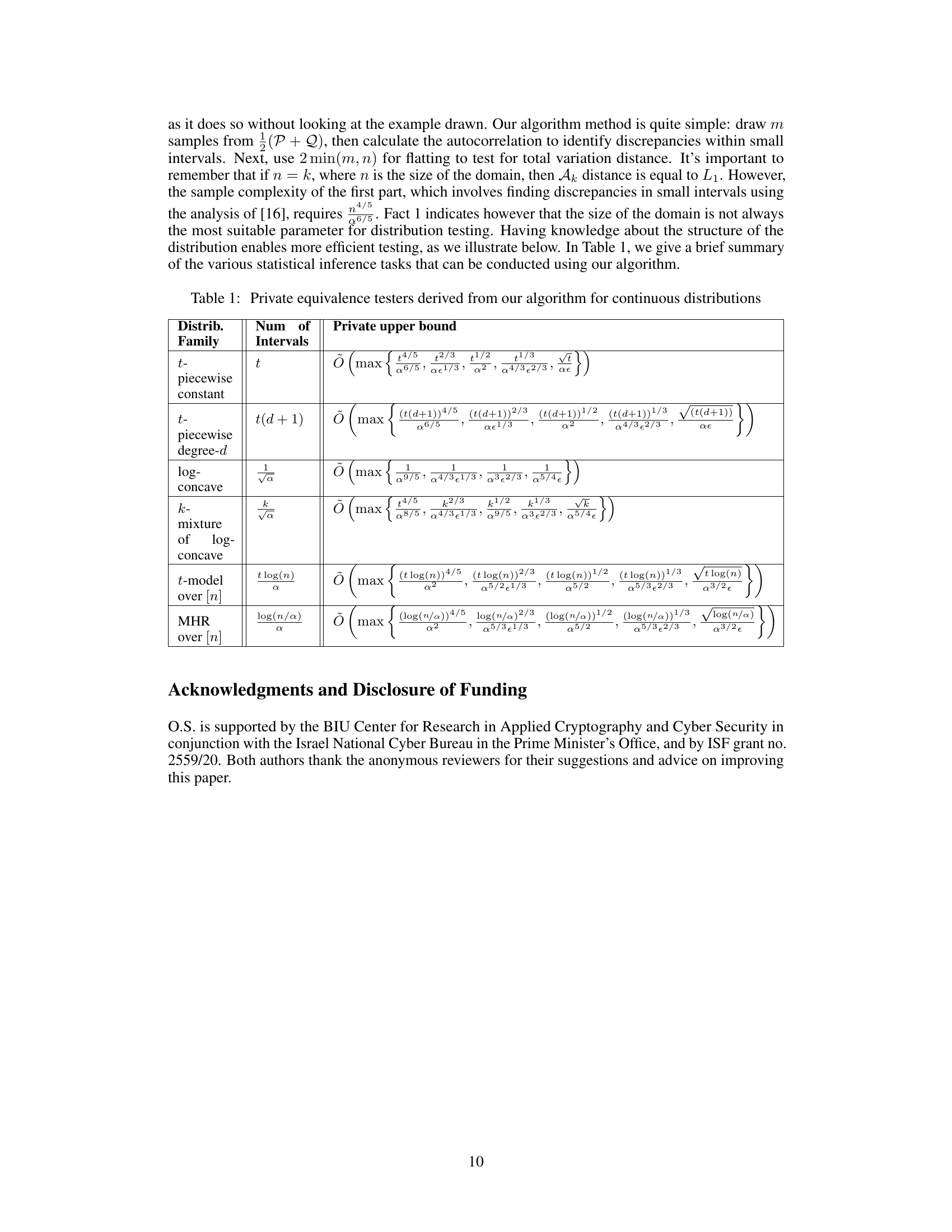
🔼 This table presents a summary of various statistical inference tasks achievable using the algorithm introduced in the paper. It shows the private upper bound on the sample complexity for different families of continuous distributions. These families include piecewise constant, piecewise degree-d, log-concave, k-mixtures of log-concave, t-model over [n], and MHR over [n]. The table lists the number of intervals required (t) for each family, and the corresponding private upper bound on the sample complexity in terms of t, k, α, and ε. This table demonstrates the algorithm’s versatility in handling various distributional structures and parameters.
read the caption
Table 1: Private equivalence testers derived from our algorithm for continuous distributions
Full paper#