TL;DR#
Communicating multiple data samples efficiently is crucial in many machine learning applications, especially in distributed or remote settings. Existing methods often rely on directly transmitting the data, leading to high communication costs, particularly when dealing with large models or numerous samples. This is particularly problematic in areas like federated learning where communication is a major bottleneck. The paper addresses this by introducing a new framework called “Universal Sample Coding”.
The core of Universal Sample Coding involves using a reference distribution, known to both sender and receiver, to estimate the target distribution from which the samples originate. By strategically using this reference distribution, the communication can be significantly compressed, thereby reducing the number of bits required for transmission. This method is applied to both federated learning and generative model scenarios demonstrating significant communication cost reduction. The theoretical analysis provides lower bounds on the achievable communication cost, and an algorithm is designed to approach this bound in practice. This showcases the potential to greatly reduce communication overhead, paving the way for more efficient applications in machine learning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in communication-efficient machine learning and distributed systems. It provides novel methods for reducing communication overhead in federated learning and generative model applications. The theoretical bounds and practical algorithms presented offer significant improvements for various applications where the transmission of multiple samples is necessary. It also opens new research avenues in exploring how this technique can improve other generative model applications and handle continuous variables.
Visual Insights#
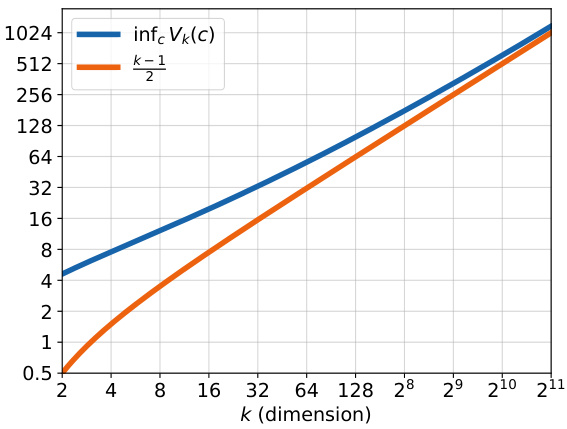
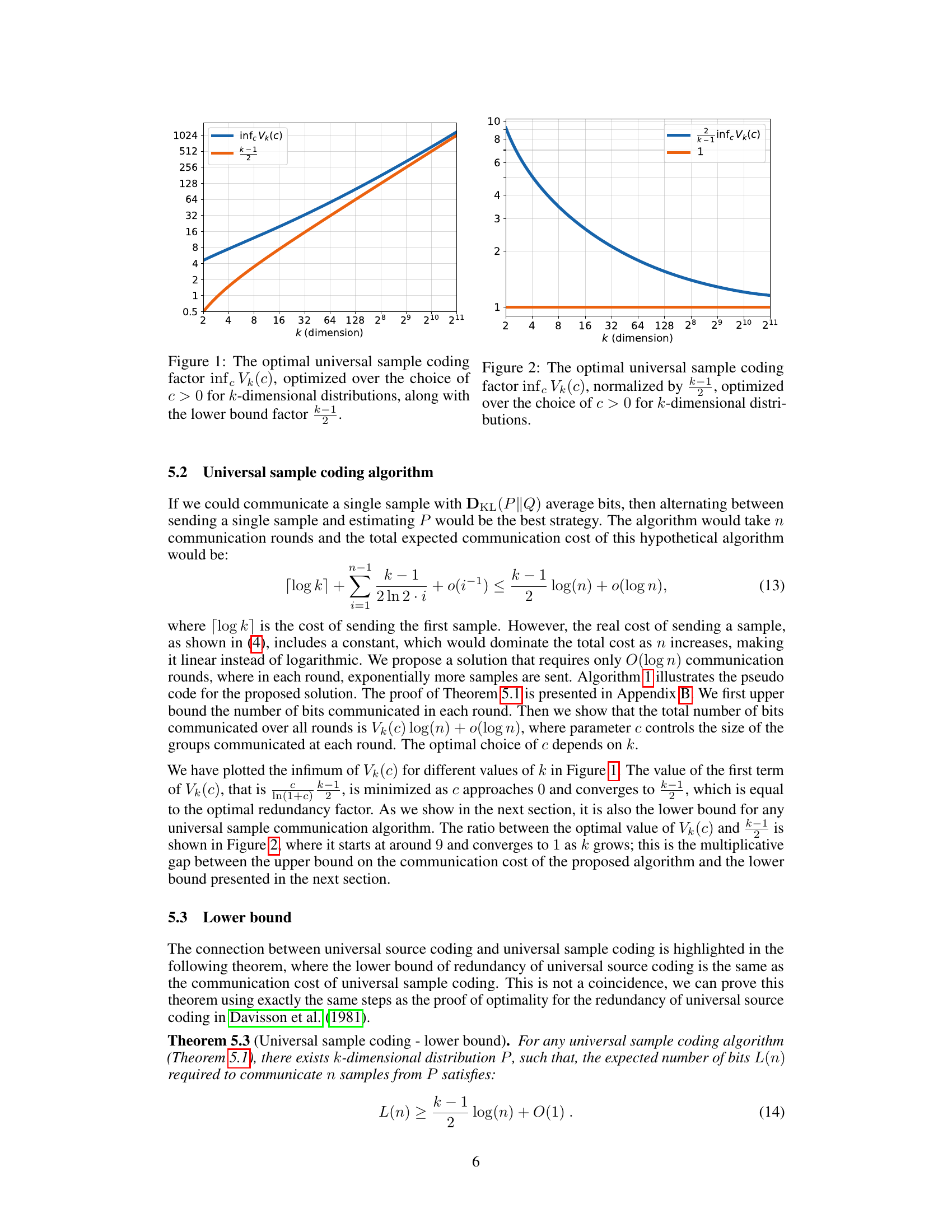
🔼 This figure shows the optimal universal sample coding factor, denoted as infc Vk(c), plotted against the dimensionality (k) of the distributions. The factor represents the multiplicative gap between the upper bound on communication cost (from the proposed algorithm) and the theoretical lower bound. The plot also includes a line representing the lower bound factor of 1, which provides a reference point for comparison. It demonstrates how the optimal factor changes as the dimensionality of the data increases.
read the caption
Figure 1: The optimal universal sample coding factor infc Vk(c), optimized over the choice of c > 0 for k-dimensional distributions, along with the lower bound factor 1.

🔼 This table summarizes the minimum number of bits required to communicate a sample from a probability distribution P to a remote decoder, under two scenarios: matched and mismatched source coding and sample communication. In matched source coding, the encoder and decoder share prior knowledge of distribution P, enabling optimal compression at the entropy H(P). In mismatched source coding, the decoder uses a different distribution Q, increasing the communication rate by the Kullback-Leibler (KL) divergence between P and Q. In sample communication, the goal is only for the receiver to obtain any sample from P, even if the specific sample from the encoder is different. In the matched case, no bits are required since shared knowledge of P enables both to sample it locally, while in mismatched scenario, only the KL-divergence cost needs to be paid.
read the caption
Table 1: Rate required to communicate a given/any sample from P
In-depth insights#
Universal Sample Coding#
The concept of Universal Sample Coding tackles the challenge of efficiently transmitting multiple samples from an unknown probability distribution. It extends traditional channel simulation by iteratively refining a reference distribution, reducing the KL-divergence between the target and reference distributions in each communication round. This results in significant communication cost savings, especially when dealing with high-dimensional data. The authors present a practical algorithm achieving near-optimal communication cost, demonstrating its effectiveness in federated learning and generative model sample communication. A key advantage lies in the algorithm’s ability to generate samples at the receiver, thus avoiding direct transmission of the complete samples. The approach also establishes a connection between sample communication and universal source coding redundancy, providing a theoretical framework. Theoretical bounds on communication cost are established and supported by empirical results. While limited by its applicability to discrete distributions, the proposed universal sample coding method offers a promising direction for more efficient communication in various machine learning applications.
Federated Learning#
The section on Federated Learning (FL) showcases the practical application of universal sample coding, significantly reducing communication overhead. It leverages the FedPM algorithm, employing probability distributions to parameterize models. Instead of transmitting entire model updates, clients send samples from their local model distributions. The central server uses these samples, along with a global model distribution, to estimate a global model update. This approach leverages channel simulation to reduce communication costs by effectively transmitting only the information that distinguishes the local client updates from the global model. The authors demonstrate a substantial 37% reduction in communication load compared to a state-of-the-art communication-efficient FL method. This highlights the efficacy and practicality of the proposed sample communication technique in real-world FL scenarios, paving the way for more efficient and scalable collaborative machine learning systems.
Generative Models#
The section on Generative Models explores the intersection of generative models and channel simulation, proposing a novel avenue for research. It highlights the potential to significantly reduce communication costs associated with generative model outputs like images, audio, and video by leveraging sample communication. Instead of generating and then compressing a sample at a central server, the proposed approach enables users to generate samples locally at significantly lower costs. This is particularly relevant for applications like text-to-image generation, where multiple samples are often generated and transmitted. The core idea rests on the observation that if a user has access to a model (Q) similar to the target generative model (P), then the amount of data needed to communicate samples from P is greatly reduced, being proportional to the KL-divergence between P and Q. This connection is not only conceptually significant but promises to alleviate the growing communication burden posed by the increasing popularity of generative AI across various applications.
Algorithm Analysis#
An algorithm analysis section for a research paper on universal sample coding would delve into the time and space complexity of the proposed coding scheme. It should quantify the computational cost associated with encoding and decoding samples, considering factors such as the number of samples, the dimensionality of the distribution, and the complexity of the probability estimation method. Scalability analysis would be crucial, demonstrating how the algorithm performs with increasing data volumes. A comparison to existing source coding techniques is necessary to highlight the advantages of the new approach. Theoretical bounds, such as the lower bound on communication cost derived in the paper, provide a benchmark for evaluating the algorithm’s efficiency and optimality. The analysis should discuss the trade-off between computational cost and communication efficiency, acknowledging any limitations or restrictions on the algorithm’s applicability. The analysis should also assess the algorithm’s robustness to noisy data or imperfect probability estimation, providing insights into its practical performance. Finally, the analysis should provide empirical results to support the theoretical findings, using experiments on various datasets and scenarios to demonstrate the effectiveness of the algorithm in different settings.
Future Directions#
The research paper’s exploration of universal sample coding opens exciting avenues. Extending the approach to continuous distributions is crucial, possibly through Bayesian estimation or model-based methods. The application to generative models, especially large language models, is promising, potentially reducing communication costs substantially. Further investigation into efficient probability estimation techniques is needed, exploring both model-based and non-parametric approaches. Improving the theoretical lower bound is a significant area; tightening the gap between the upper and lower bounds would refine the understanding of fundamental limits. Finally, assessing the robustness of the algorithm to noisy channels and the impact of non-independent samples is important for real-world applications. These are critical areas that would benefit future research.
More visual insights#
More on figures

🔼 This figure illustrates the optimal universal sample coding factor (infc Vk(c)) as a function of the dimensionality (k) of the probability distributions. The factor represents the multiplicative gap between the upper bound on the communication cost of the proposed algorithm and the theoretical lower bound. The figure shows that the optimal factor decreases as the dimensionality increases, approaching the lower bound of 1. This indicates that the efficiency of the proposed algorithm improves for higher-dimensional distributions.
read the caption
Figure 1: The optimal universal sample coding factor infc Vk(c), optimized over the choice of c > 0 for k-dimensional distributions, along with the lower bound factor 1.
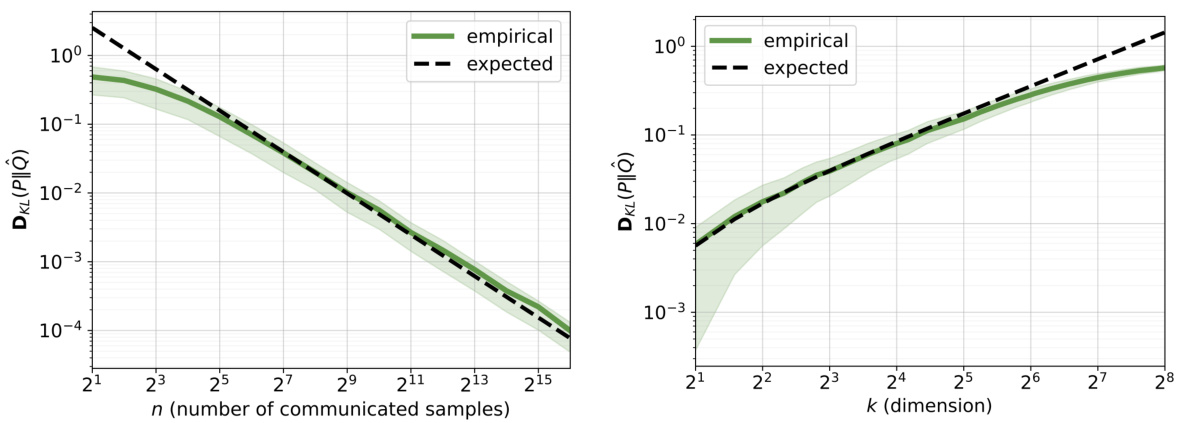
🔼 This figure shows the KL-divergence between the true probability distribution (P) and its estimate (Q) obtained using the proposed universal sample coding algorithm for different numbers of communicated samples (n). The experiment was conducted for an 8-dimensional distribution (k=8). The solid line represents the mean KL-divergence, and the shaded area represents the 20th to 80th percentiles, illustrating the variability of the estimates across multiple runs of the experiment.
read the caption
Figure 3: KL-divergence between the true and estimated probabilities for dimension k = 8, for a range of number of communicated samples n. Solid line indicates the mean, while the shaded area shows the 20th to 80th percentiles.

🔼 This figure displays the communication cost for transmitting varying numbers of samples from an 8-dimensional distribution. It compares the empirical results with the theoretical upper and lower bounds derived in the paper. The shaded region represents the 20th to 80th percentiles of the communication cost across multiple experimental runs, illustrating the variability in performance. The plot demonstrates how the observed communication cost lies between the predicted upper and lower bounds, providing experimental validation of the theoretical analysis.
read the caption
Figure 5: Communication cost of communicating n samples from an 8-dimensional distribution (k = 8). Solid line indicates the mean, while shaded area shows the 20th to 80th percentiles.
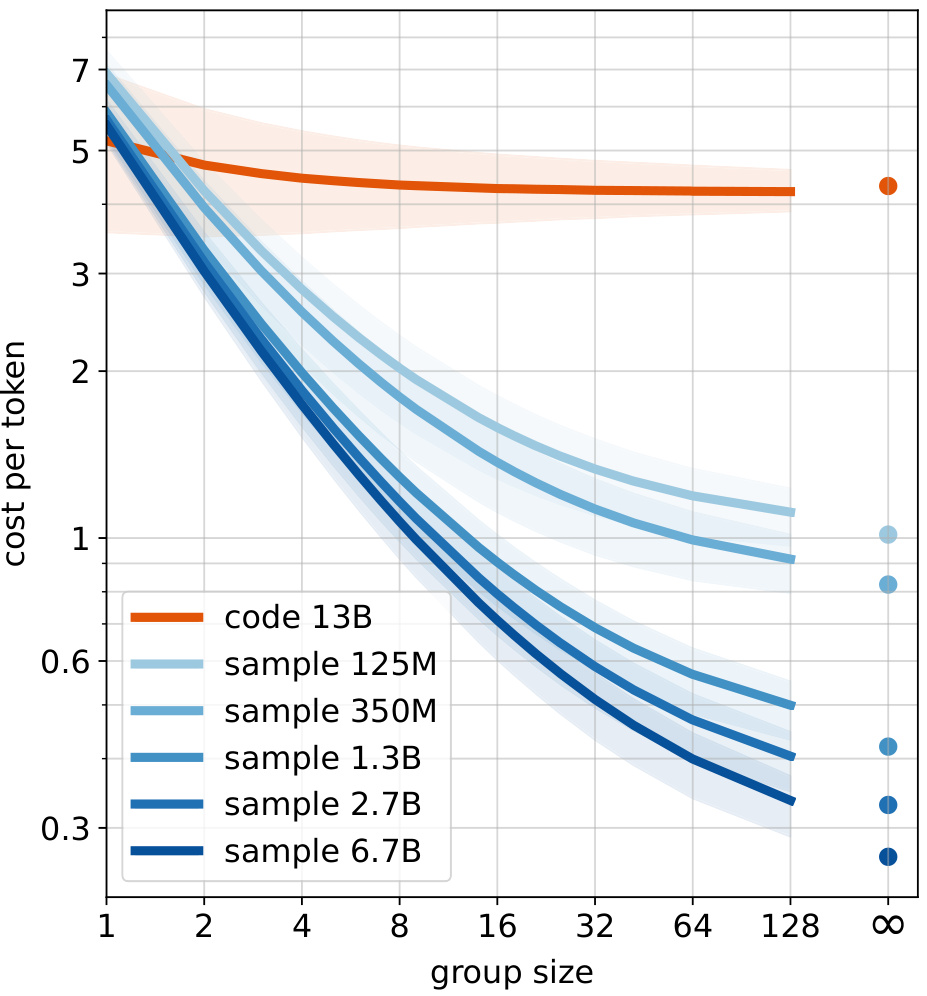
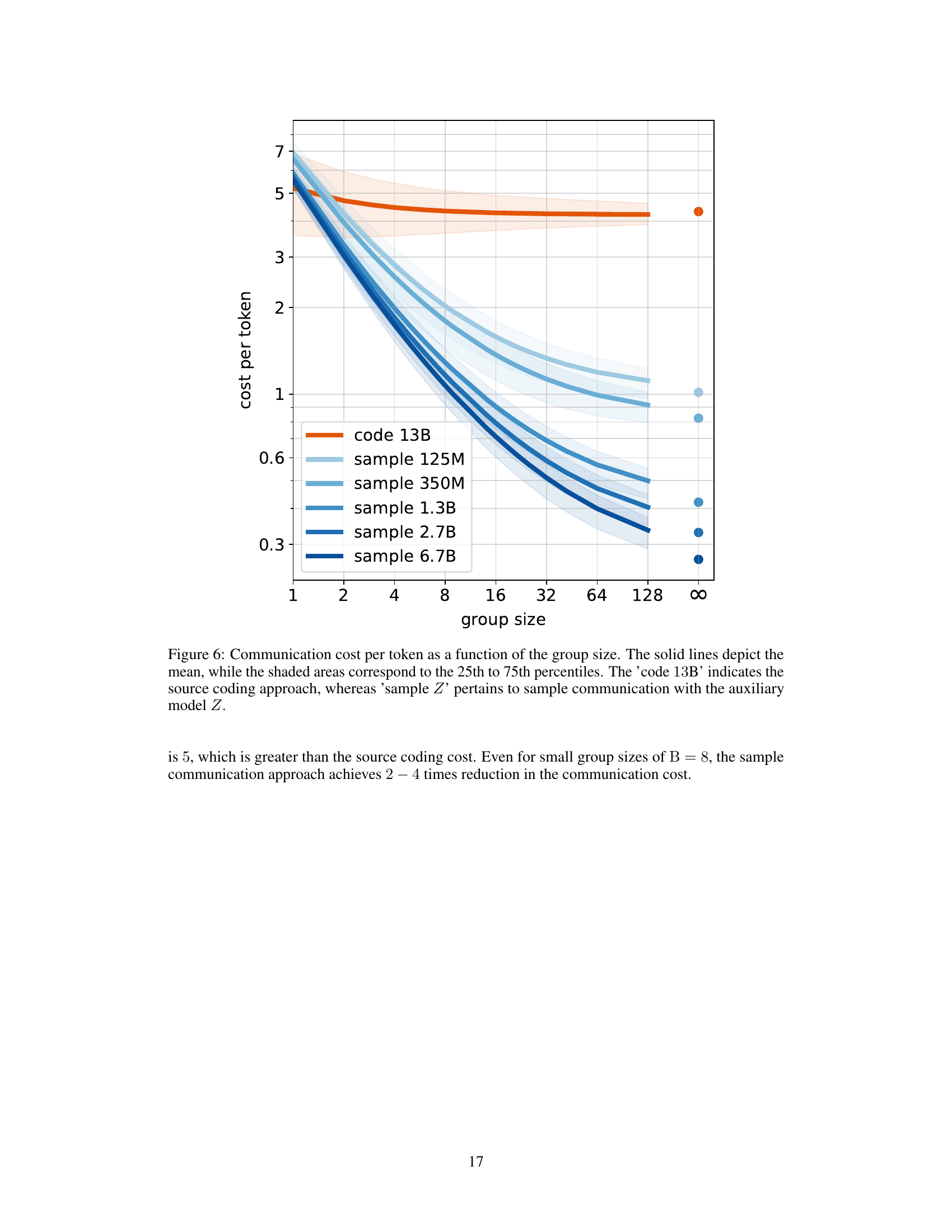
🔼 This figure shows the communication cost per token for different group sizes when using either source coding or sample communication. Source coding is the traditional method of compressing and transmitting data, while sample communication is the novel technique proposed in the paper. The figure compares the performance of sample communication using auxiliary models of varying sizes (125M, 350M, 1.3B, 2.7B, 6.7B parameters) against the source coding method. The results demonstrate that the sample communication method outperforms source coding for larger group sizes, highlighting the efficiency gains of the proposed approach.
read the caption
Figure 6: Communication cost per token as a function of the group size. The solid lines depict the mean, while the shaded areas correspond to the 25th to 75th percentiles. The ‘code 13B’ indicates the source coding approach, whereas ‘sample Z’ pertains to sample communication with the auxiliary model Z.
More on tables
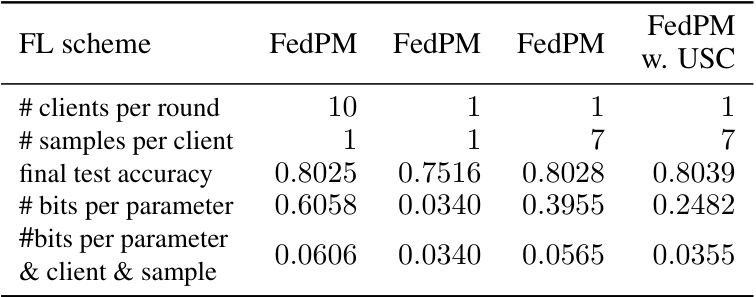
🔼 This table presents the results of applying four different Federated Probabilistic Mask Training (FedPM) schemes. The first scheme (FedPM) uses 10 clients per round and communicates 1 sample per client, achieving 80.25% test accuracy with 0.6058 bits/parameter. The second scheme (FedPM) uses only 1 client per round and 1 sample per client, resulting in lower accuracy (75.16%) but significantly less communication (0.0340 bits/parameter). The third scheme (FedPM) increases the number of samples per client to 7, while maintaining 1 client per round, leading to an accuracy of 80.28% and communication cost of 0.3955 bits/parameter. Finally, the fourth scheme (FedPM w. USC) incorporates the proposed universal sample coding (USC), using 7 samples per client and achieving the highest test accuracy (80.39%) with the lowest communication cost (0.2482 bits/parameter).
read the caption
Table 2: Accuracy and communication cost of FedPM for different simulation scenarios. Values are averaged over 20 runs, with standard deviation bellow 0.003.
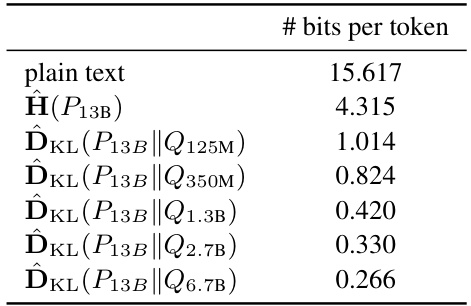
🔼 This table presents the per-token communication cost when sending samples from a 13-billion parameter language model (13B). It compares the cost of plain text transmission (15.617 bits/token), which is the entropy of the full distribution, to the costs achieved using different sizes of auxiliary models (Q) to perform sample communication. The KL-divergence between the 13B model and each auxiliary model is given, showing how much the communication cost can be reduced by using an appropriately sized auxiliary model in sample communication.
read the caption
Table 3: Per token cost of sending samples from 13B model. Entropy is a lower bound for source coding, while the KL-divergence serves as a bound for sample communication.
Full paper#