↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) in continuous environments is challenging due to the difficulty of achieving the ’no-regret’ property—guaranteeing that an algorithm’s performance converges to the optimal policy. Existing methods either rely on very specific assumptions or have regret bounds that are too large to be useful in practice. Many approaches also suffer from an unavoidable exponential dependence on the time horizon, making them unsuitable for real-world applications.
This paper addresses these issues by focusing on local linearity within continuous Markov Decision Processes (MDPs). The authors propose a new representation class called ‘Locally Linearizable MDPs’ which generalizes previous approaches. They also introduce a novel algorithm, CINDERELLA, designed to exploit this local linearity for effective learning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning (RL), especially those working with continuous state and action spaces. It introduces a novel algorithm, CINDERELLA, that achieves state-of-the-art regret bounds for a broad class of continuous MDPs, solving a major open problem in the field. Its generalizable approach using local linearity opens avenues for tackling real-world RL problems previously deemed unfeasible. The findings are essential for developing efficient and practical RL solutions, expanding the scope of RL applicability to complex systems in various domains.
Visual Insights#

This figure illustrates the core idea of Locally Linearizable MDPs. Panel (a) shows how the state-action space Z is divided into multiple regions. These regions don’t need to be geometrically regular; they can be arbitrarily shaped. Panel (b) illustrates that within each region, the Bellman operator (which updates the value function) can be approximated by a linear function of a feature map. The linear parameters (θ) can vary between regions, allowing for flexibility in modeling non-linear environments.
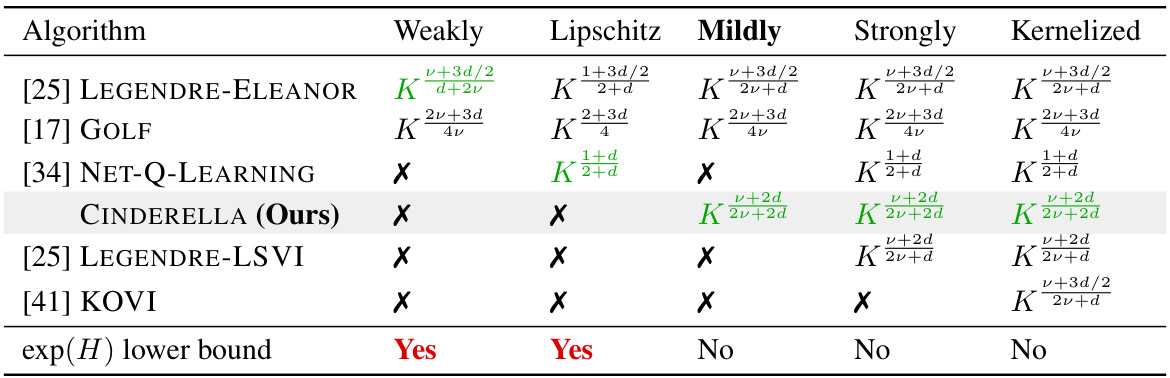
This table compares the regret bounds (in terms of the number of episodes K) achieved by different reinforcement learning algorithms on various classes of continuous Markov Decision Processes (MDPs). The MDP classes are categorized by their smoothness assumptions: Weakly Smooth, Strongly Smooth, Lipschitz, Mildly Smooth, and Kernelized. Each row represents a different algorithm, indicating whether it provides no-regret guarantees for each MDP class (X denotes no guarantee). The final row indicates whether a given MDP class is considered feasible (i.e., achievable with a polynomial regret bound in terms of the horizon H) or not (exponential lower bound). The table highlights that CINDERELLA, the algorithm proposed in this paper, provides superior regret bounds across multiple MDP classes and is the only algorithm applicable to all feasible settings.
Full paper#



















