↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Predicting rare events is notoriously difficult due to the limited data available and the long timescales involved. Traditional Monte Carlo (MC) methods struggle with the accuracy and efficiency in such scenarios. This paper focuses on policy evaluation in reinforcement learning, specifically investigating the effectiveness of temporal difference (TD) learning, a powerful algorithm for sequential data analysis. The study delves into the theoretical comparison between TD and MC, demonstrating that TD offers significant advantages, particularly in the context of rare event prediction.
The core of the research lies in proving a central limit theorem for the least-squares TD (LSTD) estimator in finite-state Markov chains. The authors provide an upper bound on the relative asymptotic variance of the LSTD estimator, revealing that it scales polynomially with the number of states, contrasting sharply with the exponential scaling observed in MC methods. This suggests that LSTD can achieve much higher accuracy with much less data than MC, especially when dealing with rare events. The paper further supports this theoretical analysis with detailed experiments on two specific problems (mean first passage time and committor function), which confirm the superior performance of LSTD, showcasing significant advantages in efficiency and accuracy.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers dealing with rare event prediction, a challenging problem across many fields. It offers novel theoretical insights into the efficiency of temporal difference learning (TD) over Monte Carlo methods, providing a stronger mathematical foundation for TD’s use in such scenarios and potentially influencing the design of future algorithms.
Visual Insights#
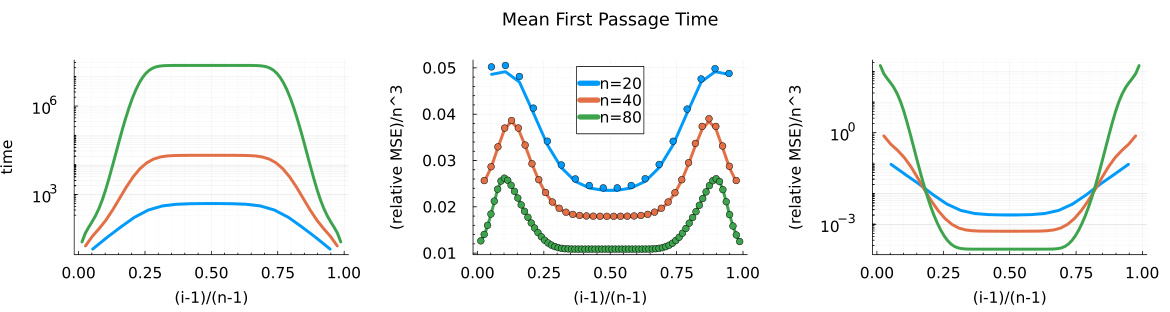
This figure compares the performance of Monte Carlo (MC) and Least-Squares Temporal Difference (LSTD) estimators for predicting the mean first passage time in a Markov chain with exponentially increasing typical escape time as the number of states (n) increases. The left panel shows the exact mean first passage time for three different values of n. The middle panel shows the relative asymptotic variance and empirical mean squared error (MSE) of the LSTD estimator with a lag time of 1. The right panel shows the exact relative asymptotic MSE of the MC estimator. The results highlight the superior performance of LSTD for this rare event prediction problem, especially as n grows large, where the MC estimator’s error increases exponentially while the LSTD estimator’s error grows much more slowly.
In-depth insights#
TD vs. MC Efficiency#
The core of the analysis revolves around comparing the efficiency of Temporal Difference (TD) learning against Monte Carlo (MC) methods, particularly for rare event prediction. A key finding highlights TD’s superior relative accuracy, especially when dealing with events that occur infrequently. This efficiency stems from TD’s ability to leverage temporal correlations within data, enabling it to learn from shorter trajectories. In contrast, MC methods need significantly longer trajectories to reach a comparable accuracy, which becomes computationally expensive and data-intensive for rare events. The study provides a mathematical framework that formalizes and substantiates this advantage, showcasing how TD’s relative asymptotic variance scales polynomially rather than exponentially with the size of the state space, a significant improvement when rare events are involved. This implies that even with limited data, TD can yield accurate predictions, effectively addressing a significant challenge in forecasting uncommon occurrences. The work also explores the effect of the trajectory length, demonstrating the presence of an optimal choice for efficient estimations.
Rare Event Prediction#
The research paper explores the intriguing challenge of rare event prediction, a problem frequently encountered in various scientific and engineering domains. The core focus lies in evaluating the efficiency of temporal difference (TD) learning, particularly the least-squares TD (LSTD) method, against the traditional Monte Carlo (MC) approach, specifically within the context of rare events. The analysis demonstrates that LSTD offers superior efficiency, achieving the desired accuracy with far fewer observed transitions compared to MC, even when dealing with events characterized by extremely long timescales. This efficiency advantage is rigorously established through theoretical analysis, including the derivation of upper bounds on the relative asymptotic variance of the LSTD estimator. The theoretical findings are supported by experimental results that showcase the polynomial scaling of LSTD’s relative variance compared to the exponential scaling of MC’s variance in the number of states. The study highlights the potential of TD learning, and LSTD in particular, for significantly enhancing the accuracy and efficiency of rare event predictions across a variety of applications.
LSTD Asymptotic Variance#
The section on ‘LSTD Asymptotic Variance’ would likely delve into a crucial theoretical analysis of the Least-Squares Temporal Difference (LSTD) algorithm’s performance. It would focus on the asymptotic behavior of the LSTD estimator’s variance, meaning the variance as the number of observed transitions approaches infinity. This is a key aspect because it informs us about the statistical efficiency of LSTD compared to other methods, particularly in the context of rare event prediction where computational cost is a significant constraint. A central limit theorem would probably be established to characterize the distribution of the LSTD estimator. The analysis would likely go further, providing a mathematical bound for the asymptotic variance; this bound would help to understand how the variance scales with parameters of the Markov chain, such as the number of states, transition probabilities, and the reward structure. The effectiveness of the LSTD method in situations with rare events heavily relies on this analysis, providing a justification for its practical advantage over other approaches like Monte Carlo methods. Comparisons to Monte Carlo’s asymptotic variance would be essential to demonstrate the superior efficiency of LSTD. Overall, this section is crucial for solidifying the theoretical foundations of LSTD’s application in rare event prediction, proving the efficiency gains mathematically.
Empirical Validations#
An Empirical Validations section in a research paper would rigorously test the claims made. It would present data from experiments designed to validate the paper’s theoretical results, including specific methodologies, data sets used, and detailed results. The section should demonstrate that the study’s findings are reliable and generalizable by showing strong statistical significance. This section would also discuss any limitations observed during validation, potential sources of error, and the robustness of results given different conditions. Visualizations, such as graphs and tables, would effectively communicate the results, and a thorough analysis would explore any unexpected outcomes, highlighting potential implications and suggesting avenues for future research. The quality of this section is crucial; it strengthens the paper’s overall credibility and scientific rigor.
Future Research#
The “Future Research” section of this paper could explore several promising avenues. Extending the theoretical framework beyond the tabular setting to encompass continuous state spaces is crucial for broader applicability. This would involve developing perturbation bounds for linear systems in continuous spaces and adapting the theoretical results to handle approximation error in continuous state Markov processes. Another important direction is investigating the effectiveness of online temporal difference learning algorithms in the context of rare event prediction, particularly addressing the slow convergence often observed in such scenarios. A detailed comparison of LSTD with other TD methods, like those employing function approximation or different update rules, would provide valuable insights into the relative strengths and weaknesses of different approaches. Finally, empirical studies focusing on real-world applications of LSTD to rare event prediction, such as in climate science, finance, or healthcare, are needed to showcase its practical utility and to identify potential limitations and areas for improvement.
More visual insights#
More on figures
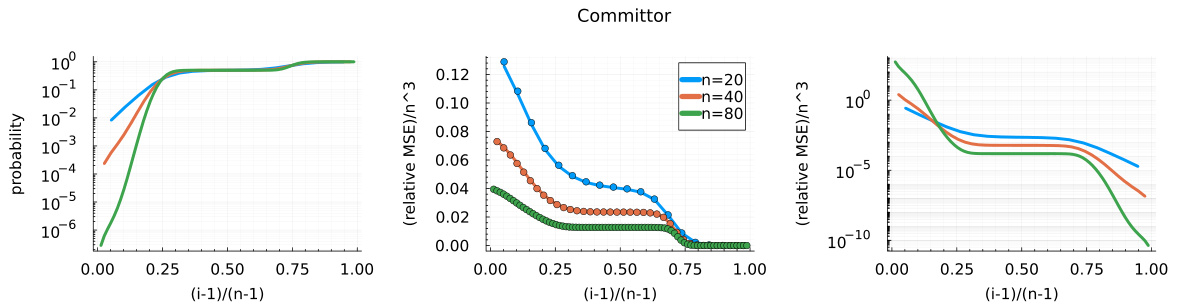
This figure compares the performance of Least Squares Temporal Difference (LSTD) and Monte Carlo (MC) methods for estimating the committor function in a one-dimensional nearest-neighbor Markov chain. The left panel shows the exact committor function for different chain sizes (n=20, 40, 80). The middle panel displays the relative asymptotic variance and empirical relative mean squared error (MSE) of the LSTD estimator, highlighting its superior performance compared to MC. The right panel shows the exact relative asymptotic MSE of the MC estimator.
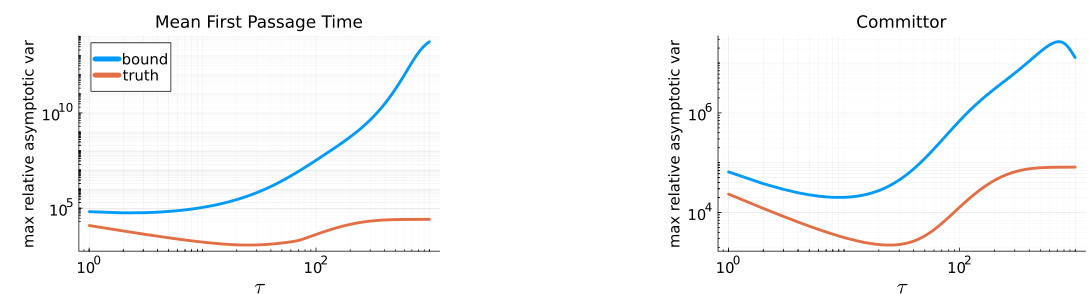
This figure compares the theoretical bounds and the actual values for the maximum relative asymptotic variance of the mean first passage time and committor estimators as a function of the lag time (τ). The number of states (n) is fixed at 40. The plot shows how the theoretical bounds from equations (6) and (7) relate to the actual behavior of the estimators. The results highlight how the choice of lag time significantly impacts the variance, and for a particular τ value, the variance of the LSTD estimator is much lower than the variance of the MC estimator.

This figure compares the performance of Monte Carlo (MC) and Least-Squares Temporal Difference (LSTD) estimators for predicting the mean first passage time in a Markov chain with different numbers of states (n=20, 40, 80). The left panel shows the exact mean first passage times, highlighting the exponentially increasing timescale of rare events as the number of states grows. The middle panel presents the relative asymptotic variance and empirical relative mean squared error (MSE) of the LSTD estimator, demonstrating its superior performance compared to MC (right panel). The empirical MSE confirms the theoretical results, especially regarding how MC error increases exponentially as the number of states increase, while the LSTD estimator grows far more slowly. This illustrates the efficiency of LSTD, even in scenarios involving rare events.

The left panel shows a graph where edge thickness represents the transition probability between nodes. The right panel is the same graph after removing edges with probabilities below a certain threshold, resulting in a ‘minorizing graph’. This illustrates the concept of a minorizing graph used in the paper’s theoretical analysis.
Full paper#



















