TL;DR#
Current neural architecture search (NAS) methods struggle to generate truly novel architectures, often producing incremental improvements over existing designs. This is largely due to their limited and often unexpressive search spaces, which restrict the range of possible architectures that can be explored. The inherent limitations of these spaces hinder the exploration of fundamentally different architectural paradigms and limit the potential of NAS to drive transformative progress in the field.
To address these challenges, the paper introduces “einspace,” a highly expressive search space based on a probabilistic context-free grammar. Einspace is designed to support a wide range of architectures with various complexities, including many state-of-the-art designs. Experiments demonstrate that Einspace consistently finds competitive architectures and achieves significant improvements when initialized with strong baselines. The use of simple search algorithms highlights the expressivity of the space and suggests that further advancements are possible using more sophisticated techniques. This work represents a key step towards a more transformative NAS paradigm that emphasizes search space expressivity and strategic initialization.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel and highly expressive search space for neural architecture search (NAS), addressing a key limitation in the field. Its flexibility allows for the discovery of architectures beyond the typical, opening new avenues for research and potentially leading to more innovative and high-performing neural networks. The use of simple search strategies to achieve competitive results suggests further improvements are possible with more sophisticated methods. This work will inspire further research into expressive search space design and more effective search strategies for NAS.
Visual Insights#
🔼 This figure shows three state-of-the-art neural network architectures (ResNet18, ViT, and MLP-Mixer) and their corresponding derivation trees within the proposed einspace search space. The top row displays the architectures, where the black node represents the input tensor and the red node signifies the output. The bottom row illustrates the derivation trees generated by the context-free grammar used to define einspace. In the derivation trees, the top node represents the starting symbol of the grammar, grey nodes represent non-terminal symbols (intermediate steps in architecture generation), and leaf nodes depict the terminal operations (the actual layers in the neural network). The color-coding of the nodes provides information about the type of operation represented (explained in section 3.1 of the paper).
read the caption
Figure 1: Three state-of-the-art architectures and their associated derivation trees within einspace. Top row shows the architectures where the black node is the input tensor and the red is the output. Bottom row shows derivation trees where the top node represents the starting symbol, the grey internal nodes the non-terminals and the leaf nodes the terminal operations. See Section 3.1 for details on other node colouring. Best viewed with digital zoom.
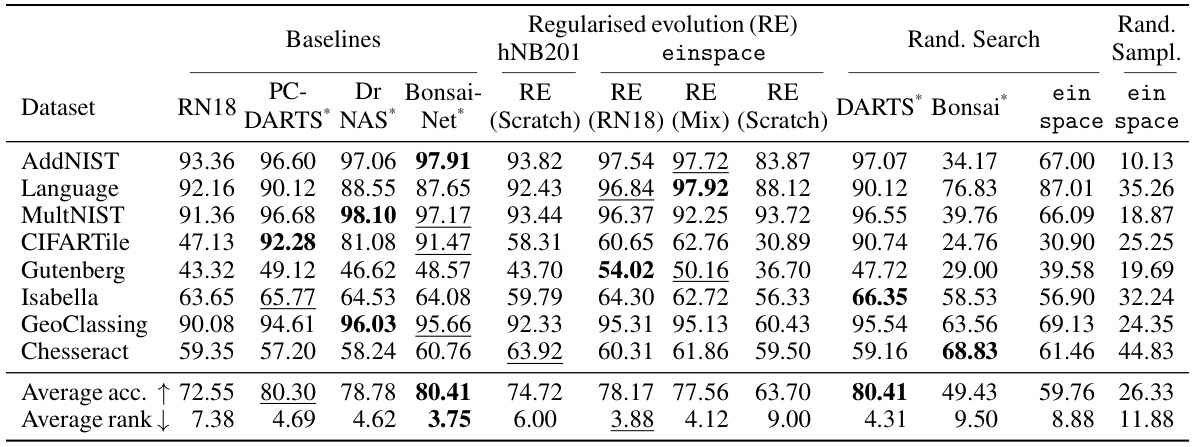
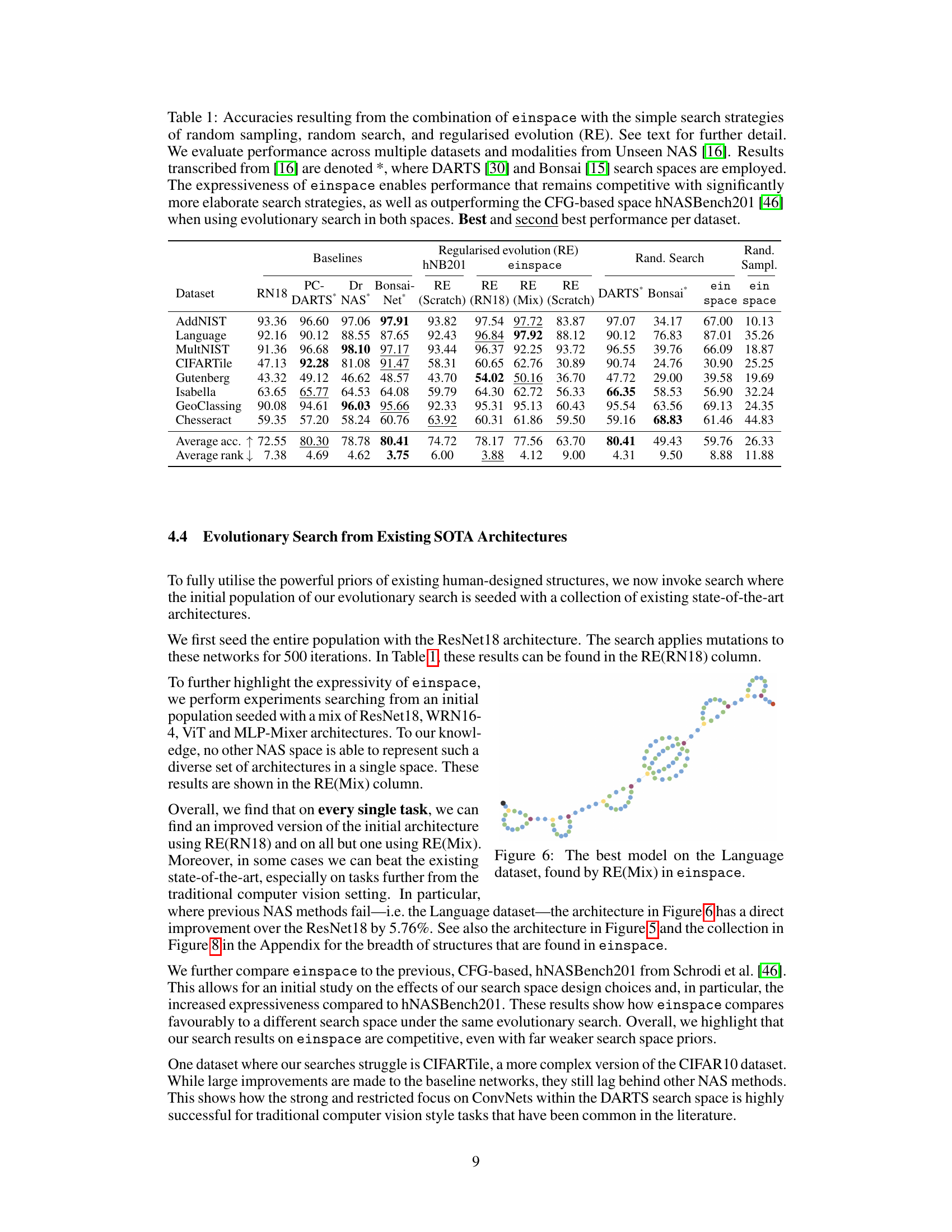
🔼 This table presents the accuracy results achieved by employing various search strategies (random sampling, random search, and regularized evolution) within the proposed einspace search space. It compares the performance of einspace against several established NAS methods (PC-DARTS, DrNAS, Bonsai-Net) on eight diverse tasks from the Unseen NAS benchmark. The table highlights the impact of the expressive nature of einspace, demonstrating competitive results even with relatively simple search strategies. It also shows that einspace outperforms existing CFG-based spaces such as hNASBench201 when evolutionary search is used.
read the caption
Table 1: Accuracies resulting from the combination of einspace with the simple search strategies of random sampling, random search, and regularised evolution (RE). See text for further detail. We evaluate performance across multiple datasets and modalities from Unseen NAS [16]. Results transcribed from [16] are denoted *, where DARTS [30] and Bonsai [15] search spaces are employed. The expressiveness of einspace enables performance that remains competitive with significantly more elaborate search strategies, as well as outperforming the CFG-based space hNASBench201 [46] when using evolutionary search in both spaces. Best and second best performance per dataset.
In-depth insights#
Einspace Search Space#
The Einspace search space, as presented in the research paper, is a significant advancement in neural architecture search (NAS). Its core innovation lies in its expressiveness, moving beyond the limitations of previous search spaces that often favored specific architectural patterns like convolutional networks. Einspace leverages a parameterized probabilistic context-free grammar (PCFG) to define a highly flexible search space capable of representing a vast range of network architectures including ResNets, Transformers, and MLP-Mixers. This expressiveness allows for the exploration of fundamentally different network designs, going beyond incremental improvements and potentially leading to novel architectural breakthroughs. The use of a PCFG allows for complex structures, diverse operations, and various sizes, greatly enhancing the search space’s versatility. However, the expressiveness also poses challenges. The sheer size of Einspace increases search complexity, demanding carefully crafted search strategies to avoid getting lost in the vast space. Strategic search initialization using strong baseline architectures becomes crucial to efficiently guide the search towards high-performing models. The incorporation of probabilistic extensions and carefully balanced priors within the grammar is a key factor in managing the search space’s complexity and ensuring the generation of valid architectures.
CFG-based NAS#
CFG-based Neural Architecture Search (NAS) leverages the power of context-free grammars to represent and explore the space of possible neural network architectures. This approach offers several advantages. First, CFGs provide a structured and elegant way to define a search space, allowing for the systematic generation and evaluation of architectures with varying levels of complexity and diversity. Second, CFGs can encode high-level design principles and biases, enabling the incorporation of prior knowledge and inductive biases from existing architectures. This can significantly improve search efficiency and the quality of discovered architectures. Third, CFGs enable the exploration of a vastly larger and more diverse search space than many other NAS methods that often rely on restrictive cell-based or other limited approaches. This flexibility translates to greater potential for discovering novel and more powerful network architectures. However, challenges remain. The expressivity of CFG-based NAS can also lead to computationally expensive searches. Careful design of the grammar and the choice of search algorithms are crucial for balancing exploration, exploitation, and computational cost. Furthermore, the interpretation and analysis of the generated architectures can be complex, particularly for highly intricate grammars. Despite these difficulties, CFG-based NAS offers a promising and flexible framework for advancing the field and remains an active area of research, particularly concerning the development of more sophisticated search strategies and scalable approaches.
Unseen NAS Results#
An analysis of ‘Unseen NAS Results’ would necessitate a detailed examination of the paper’s experimental methodology and findings. It would likely involve a discussion of the specific datasets used within the Unseen NAS benchmark, a comparison to existing state-of-the-art models on those same datasets, and an assessment of the performance gains achieved by the new search space. Key aspects to analyze would include the choice of search algorithm, metrics used to evaluate performance, and any statistical significance testing performed. A crucial element would be the identification of novel architectures discovered, which would showcase the ability of the search space to generate non-trivial and effective designs. Additionally, a comparison to the performance of random search would highlight the impact of the proposed method on the efficiency and effectiveness of the NAS process. Attention should be given to potential limitations, including computational cost, the potential for overfitting to specific datasets, and the potential for lack of generalizability to other tasks. Overall, the analysis should critically evaluate the strength and implications of the reported Unseen NAS results to determine if the new search space presents a significant advancement in the field of neural architecture search.
Evolutionary Search#
Evolutionary search, in the context of neural architecture search (NAS), is a powerful optimization strategy that mimics natural selection. It involves generating a population of neural network architectures, evaluating their performance on a target task, and iteratively selecting the best-performing architectures to create new, improved generations. This process leverages mechanisms like mutation (introducing random changes) and crossover (combining features of successful architectures) to explore the vast search space of possible designs. Unlike gradient-based methods, evolutionary search doesn’t rely on calculating gradients, making it suitable for complex, non-differentiable search spaces. However, its effectiveness heavily depends on the choice of evolutionary operators, population size, and selection criteria. The computational cost of evolutionary search can be substantial, as it necessitates training numerous architectures during each iteration. Despite this, the capacity to discover novel architectures and improve upon existing ones makes evolutionary search a compelling approach, particularly when combined with well-defined search spaces and informative initialization strategies.
Future of NAS#
The future of Neural Architecture Search (NAS) hinges on addressing its current limitations. Increased search space expressivity is crucial, moving beyond the relatively narrow spaces currently employed to explore truly novel architectures, potentially incorporating elements from diverse paradigms like transformers and MLP-Mixers. More efficient search algorithms are needed to navigate these expanded spaces, possibly involving techniques like learning search space probabilities or leveraging hierarchical search strategies. Improved search initialization with strong baselines or human-designed architectures can significantly boost performance, reducing the need for extensive exploration from scratch. Greater attention to task diversity and benchmark design is also key, ensuring the robustness and generalizability of discovered architectures across a wider range of applications. Finally, integrating NAS with other AI advancements, such as automated machine learning and transfer learning techniques, holds enormous potential to simplify the process and further unlock the transformative power of NAS.
More visual insights#
More on figures

🔼 This figure shows three state-of-the-art neural network architectures (ResNet18, ViT, and MLP-Mixer) and their corresponding derivation trees within the proposed einspace search space. The top row displays the architectures visually, with the input tensor represented by a black node and the output tensor by a red node. The bottom row illustrates the derivation trees generated by the parameterized probabilistic context-free grammar (PCFG) that defines einspace. Each derivation tree shows how the architecture is constructed from fundamental operations, with the top node as the starting symbol, gray internal nodes representing non-terminal operations, and leaf nodes representing terminal operations. Different colors are used to distinguish the type of operation (branching, aggregation, routing, computation) as explained in Section 3.1.
read the caption
Figure 1: Three state-of-the-art architectures and their associated derivation trees within einspace. Top row shows the architectures where the black node is the input tensor and the red is the output. Bottom row shows derivation trees where the top node represents the starting symbol, the grey internal nodes the non-terminals and the leaf nodes the terminal operations. See Section 3.1 for details on other node colouring. Best viewed with digital zoom.

🔼 This figure shows three state-of-the-art neural network architectures (ResNet18, ViT, and MLP-Mixer) and their corresponding derivation trees within the proposed einspace search space. Each architecture is represented visually with the input tensor in black and the output in red. The derivation trees illustrate how these architectures are constructed from fundamental operations within einspace, using a context-free grammar. The top node of the tree represents the starting symbol of the grammar. Internal nodes are non-terminals and represent modules, while the leaf nodes are terminal operations, each colored to represent their operational role.
read the caption
Figure 1: Three state-of-the-art architectures and their associated derivation trees within einspace. Top row shows the architectures where the black node is the input tensor and the red is the output. Bottom row shows derivation trees where the top node represents the starting symbol, the grey internal nodes the non-terminals and the leaf nodes the terminal operations. See Section 3.1 for details on other node colouring. Best viewed with digital zoom.

🔼 This figure shows three state-of-the-art neural network architectures (ResNet18, ViT, and MLP-Mixer) and their corresponding derivation trees within the proposed einspace search space. The top row displays the architectures visually, with the input tensor represented by a black node and the output tensor by a red node. The bottom row illustrates the derivation trees for each architecture, showing how they are generated by the context-free grammar used to define einspace. The top node in each derivation tree is the starting symbol, grey nodes represent non-terminal operations, and leaf nodes represent the terminal operations used in the architecture. Different colors are used to visually represent different groups of operations in the derivation trees.
read the caption
Figure 1: Three state-of-the-art architectures and their associated derivation trees within einspace. Top row shows the architectures where the black node is the input tensor and the red is the output. Bottom row shows derivation trees where the top node represents the starting symbol, the grey internal nodes the non-terminals and the leaf nodes the terminal operations. See Section 3.1 for details on other node colouring. Best viewed with digital zoom.
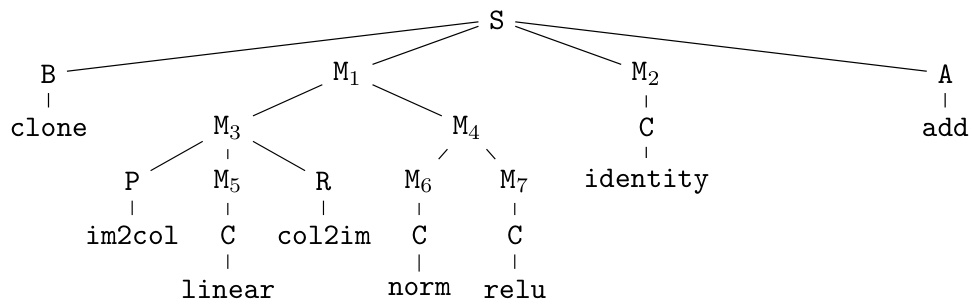
🔼 This figure shows the derivation tree for a simple convolutional block with a skip connection, constructed using the einspace context-free grammar. The tree visually represents how fundamental operations (leaf nodes) combine to form larger modules (internal nodes) and ultimately, the complete architecture (root node). It illustrates the hierarchical and recursive nature of the grammar, enabling the generation of diverse and complex architectures.
read the caption
Figure 3: Example derivation tree of a traditional convolutional block with a skip connection.
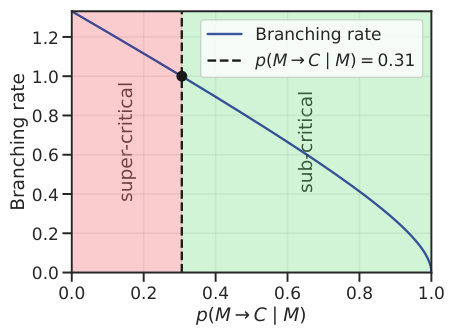
🔼 This figure shows a graph illustrating the relationship between the branching rate and the probability of selecting a computation module (p(M→C|M)) in the CFG. The x-axis represents p(M→C|M), and the y-axis represents the branching rate. The curve represents the boundary between the super-critical and sub-critical regions. The super-critical region (pink) indicates a high branching rate where the CFG can generate infinitely long architectures. The sub-critical region (green) indicates a low branching rate, ensuring that the CFG generates finite architectures. A dashed vertical line indicates a threshold probability of p(M→C|M) = 0.31. A black point on the curve shows that with a p(M→C|M) slightly below 0.31, the branching rate is slightly above 1. Therefore, the probability p(M→C|M) is set to be > 0.31 to guarantee that the CFG is in the sub-critical region and does not generate infinitely long architectures.
read the caption
Figure 4: To ensure our CFG is consistent and does not generate infinite architectures, we make sure the branching rate is in the sub-critical region by setting p(M→C|M)>0.31.

🔼 This figure showcases the top-performing architecture discovered by the Regularized Evolution (RE) algorithm initialized with a mix of state-of-the-art architectures (RE(Mix)) on the AddNIST dataset, within the einspace search space. The architecture’s structure and complexity are visually represented, highlighting the capacity of einspace to find diverse and high-performing architectures.
read the caption
Figure 5: The top RE(Mix) architecture on AddNIST, found in einspace.

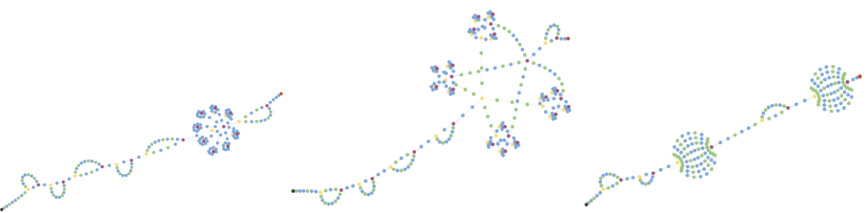
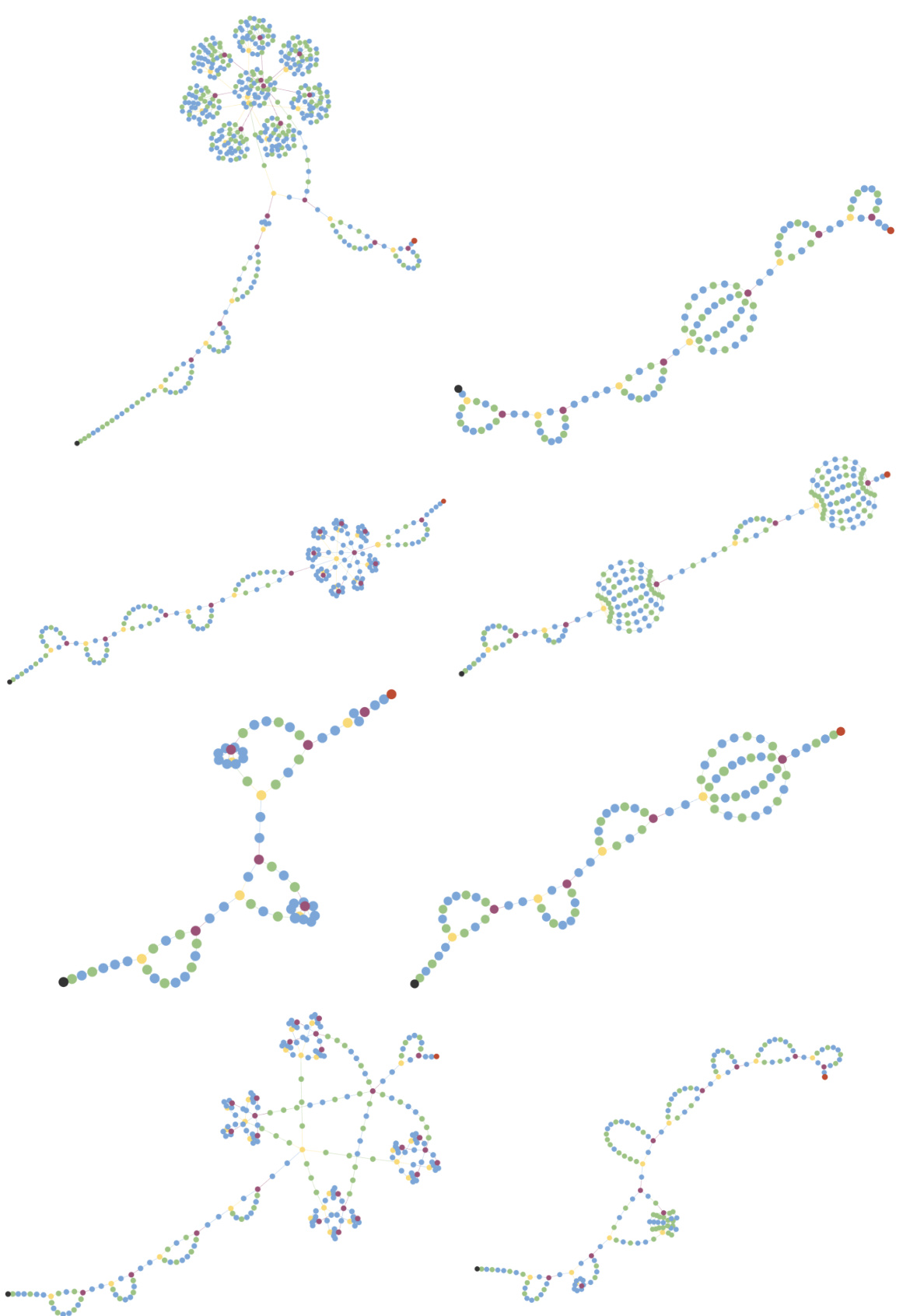
🔼 This figure visualizes the top-performing neural network architectures discovered by the regularized evolution (RE) algorithm initialized with a mix of state-of-the-art architectures (RE(Mix)) in the einspace search space. Each sub-figure represents a different dataset from the Unseen NAS benchmark: AddNIST, Language, MultNIST, CIFAR-Tile, Gutenberg, Isabella, GeoClassing, and Chesseract. The architectures are depicted graphically, with each node representing a specific operation (e.g., convolution, normalization, activation), and the color indicating the node type. The figure demonstrates the diversity of architectures generated by the einspace search space, highlighting its capability to discover novel and high-performing architectures across various tasks.
read the caption
Figure 8: The top architectures found by RE(Mix) in einspace on Unseen NAS. From left to right, row by row: AddNIST, Language; MultNIST, CIFARTile; Gutenberg, Isabella; GeoClassing, Chesseract.

🔼 This figure shows three state-of-the-art neural architectures (ResNet18, ViT, MLP-Mixer) and how they are represented as derivation trees within the proposed einspace search space. The top row displays the architectures visually, highlighting input and output tensors. The bottom row presents the corresponding derivation trees generated by the context-free grammar, illustrating how the architectures are constructed from fundamental operations. Each node in the tree represents an operation or module, with the terminal nodes signifying fundamental operations and non-terminal nodes representing more complex modules. The node colors represent different types of operations. This visualization demonstrates the expressiveness of einspace in representing diverse architectures.
read the caption
Figure 1: Three state-of-the-art architectures and their associated derivation trees within einspace. Top row shows the architectures where the black node is the input tensor and the red is the output. Bottom row shows derivation trees where the top node represents the starting symbol, the grey internal nodes the non-terminals and the leaf nodes the terminal operations. See Section 3.1 for details on other node colouring. Best viewed with digital zoom.

🔼 This figure illustrates how three different state-of-the-art neural network architectures (ResNet18, ViT, and MLP-Mixer) are represented within the einspace search space using derivation trees. Each architecture’s derivation tree shows how the architecture is built up from fundamental operations, illustrating the expressiveness of the proposed search space. The top row displays the architectures, while the bottom row shows their respective derivation trees. The nodes in the derivation trees represent different operations and their connections in the architecture, using different colors to distinguish various types of operations.
read the caption
Figure 1: Three state-of-the-art architectures and their associated derivation trees within einspace. Top row shows the architectures where the black node is the input tensor and the red is the output. Bottom row shows derivation trees where the top node represents the starting symbol, the grey internal nodes the non-terminals and the leaf nodes the terminal operations. See Section 3.1 for details on other node colouring. Best viewed with digital zoom.
🔼 This figure shows three state-of-the-art neural network architectures (ResNet18, ViT, and MLP-Mixer) and their corresponding derivation trees within the einspace search space. The top row displays the architectures themselves, illustrating the flow of tensors from input (black) to output (red). The bottom row shows the derivation trees generated by the probabilistic context-free grammar (PCFG) that defines the einspace search space. These trees break down each architecture into a hierarchical structure of fundamental operations (leaf nodes), non-terminal operations (grey nodes), and the starting symbol (top node). The color-coding of nodes in the trees provides further information about the operation type (detailed in Section 3.1), showing how complex architectures are built from simpler operations within the grammar.
read the caption
Figure 1: Three state-of-the-art architectures and their associated derivation trees within einspace. Top row shows the architectures where the black node is the input tensor and the red is the output. Bottom row shows derivation trees where the top node represents the starting symbol, the grey internal nodes the non-terminals and the leaf nodes the terminal operations. See Section 3.1 for details on other node colouring. Best viewed with digital zoom.
More on tables

🔼 This table presents the accuracy results obtained by applying three different search strategies (random sampling, random search, and regularized evolution) within the einspace search space on eight diverse datasets from the Unseen NAS benchmark. It compares einspace’s performance to several baselines from the literature (PC-DARTS, DrNAS, Bonsai-Net, and a ResNet18) using the same datasets and metrics. The table highlights the competitive performance achieved by einspace, particularly with regularized evolution, even when using simple search algorithms, demonstrating its effectiveness in discovering high-performing architectures. It also shows superior performance compared to the hNASBench201 search space when using evolutionary search.
read the caption
Table 1: Accuracies resulting from the combination of einspace with the simple search strategies of random sampling, random search, and regularised evolution (RE). See text for further detail. We evaluate performance across multiple datasets and modalities from Unseen NAS [16]. Results transcribed from [16] are denoted *, where DARTS [30] and Bonsai [15] search spaces are employed. The expressiveness of einspace enables performance that remains competitive with significantly more elaborate search strategies, as well as outperforming the CFG-based space hNASBench201 [46] when using evolutionary search in both spaces. Best and second best performance per dataset.

🔼 This table presents the results of three different search strategies (random sampling, random search, and regularized evolution) applied to the einspace search space on several datasets from the Unseen NAS benchmark. It compares the performance of einspace against several baselines from the literature, highlighting its competitive performance, especially when using the regularized evolution strategy.
read the caption
Table 1: Accuracies resulting from the combination of einspace with the simple search strategies of random sampling, random search, and regularised evolution (RE). See text for further detail. We evaluate performance across multiple datasets and modalities from Unseen NAS [16]. Results transcribed from [16] are denoted *, where DARTS [30] and Bonsai [15] search spaces are employed. The expressiveness of einspace enables performance that remains competitive with significantly more elaborate search strategies, as well as outperforming the CFG-based space hNASBench201 [46] when using evolutionary search in both spaces. Best and second best performance per dataset.
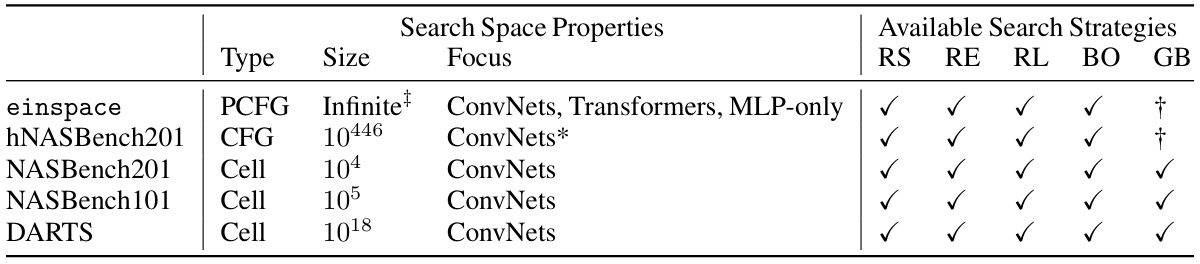
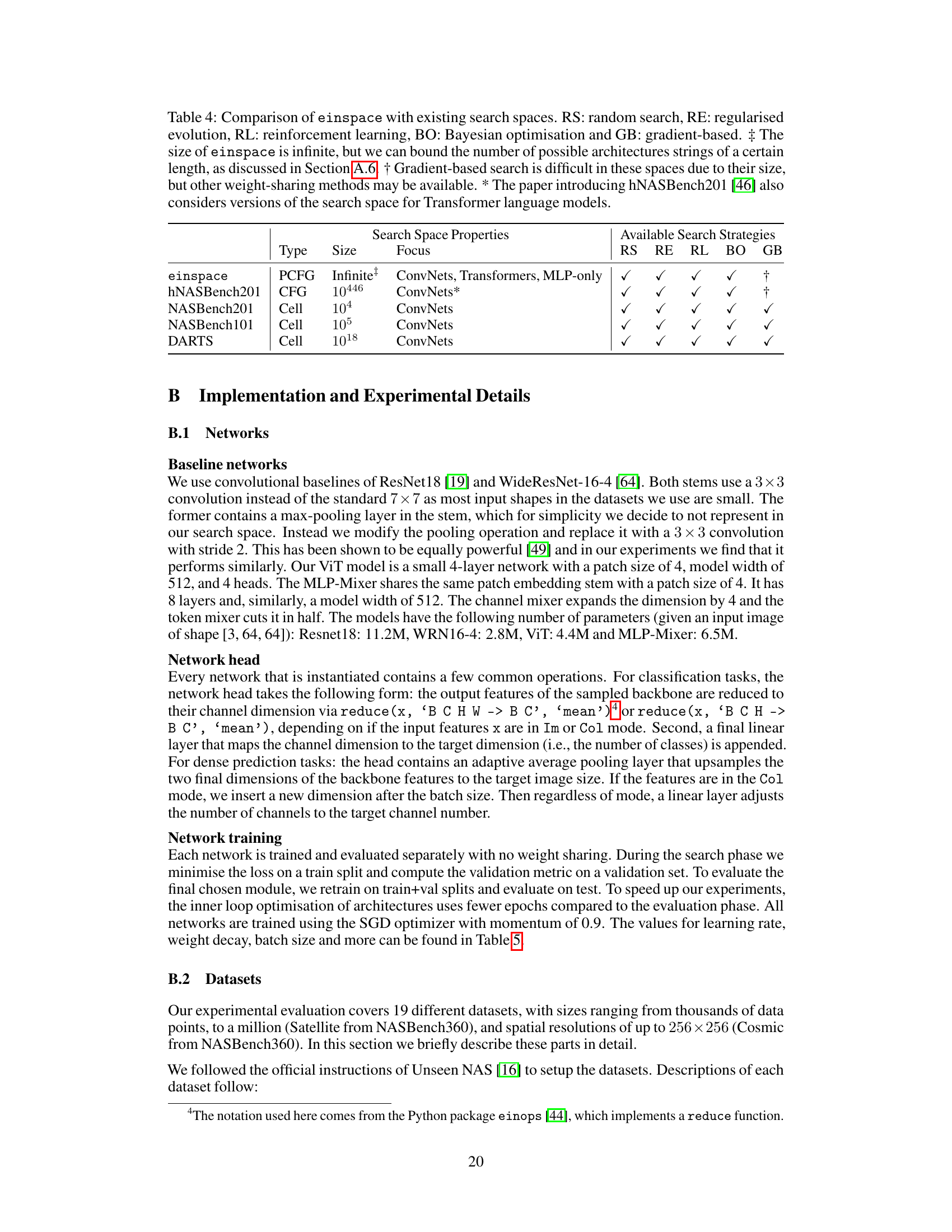
🔼 This table compares the properties of the proposed einspace search space with four other existing search spaces in the literature. The comparison is made based on the type of grammar used (PCFG, CFG, Cell), size of the space (finite or infinite), the focus of the space (ConvNets, Transformers, MLP, etc.), and the available search strategies (RS, RE, RL, BO, GB). It also includes notes regarding specific characteristics of the spaces.
read the caption
Table 4: Comparison of einspace with existing search spaces. RS: random search, RE: regularised evolution, RL: reinforcement learning, BO: Bayesian optimisation and GB: gradient-based. ‡ The size of einspace is infinite, but we can bound the number of possible architectures strings of a certain length, as discussed in Section A.6. † Gradient-based search is difficult in these spaces due to their size, but other weight-sharing methods may be available. * The paper introducing hNASBench201 [46] also considers versions of the search space for Transformer language models.

🔼 This table presents the results of using three different search strategies (random sampling, random search, and regularized evolution) within the proposed einspace search space, compared to various baselines from the literature. The results are shown across eight diverse datasets from the Unseen NAS benchmark [16], covering various modalities (vision, language, audio, chess). The table highlights the performance gains achieved by using einspace, especially when employing regularized evolution, and demonstrates its competitiveness against more complex search strategies and other state-of-the-art search spaces like hNASBench201.
read the caption
Table 1: Accuracies resulting from the combination of einspace with the simple search strategies of random sampling, random search, and regularised evolution (RE). See text for further detail. We evaluate performance across multiple datasets and modalities from Unseen NAS [16]. Results transcribed from [16] are denoted *, where DARTS [30] and Bonsai [15] search spaces are employed. The expressiveness of einspace enables performance that remains competitive with significantly more elaborate search strategies, as well as outperforming the CFG-based space hNASBench201 [46] when using evolutionary search in both spaces. Best and second best performance per dataset.
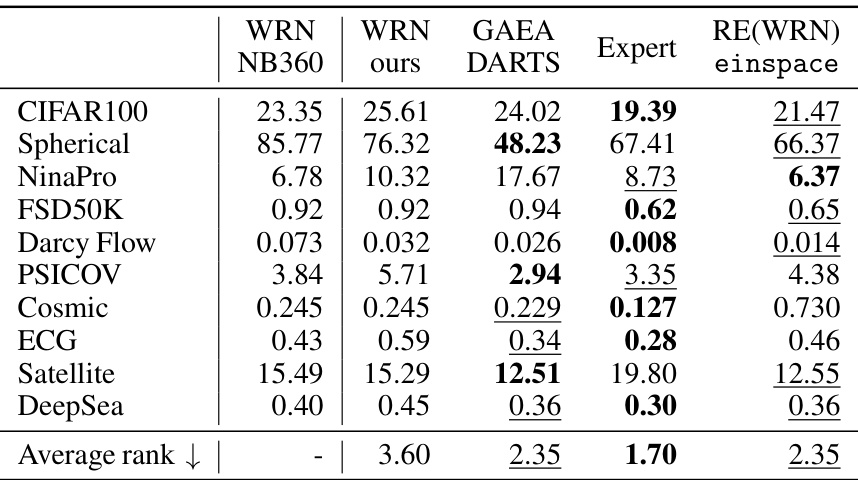
🔼 This table presents the results of three different search strategies (random sampling, random search, and regularized evolution) applied to the einspace search space on eight diverse datasets from the Unseen NAS benchmark. It compares the performance of these strategies against several baselines (ResNet18, PC-DARTS, DrNAS, Bonsai-Net) from previous work. The table shows that even simple search strategies in the expressive einspace can achieve competitive results, and that the performance of the regularized evolution approach surpasses other baseline methods in multiple datasets. The table also provides a comparison to the results of using another CFG-based search space (hNASBench201) demonstrating the superior performance of the proposed method.
read the caption
Table 1: Accuracies resulting from the combination of einspace with the simple search strategies of random sampling, random search, and regularised evolution (RE). See text for further detail. We evaluate performance across multiple datasets and modalities from Unseen NAS [16]. Results transcribed from [16] are denoted *, where DARTS [30] and Bonsai [15] search spaces are employed. The expressiveness of einspace enables performance that remains competitive with significantly more elaborate search strategies, as well as outperforming the CFG-based space hNASBench201 [46] when using evolutionary search in both spaces. Best and second best performance per dataset.

🔼 This table presents the results of three different search strategies (random sampling, random search, and regularized evolution) applied to the einspace search space on eight diverse datasets from the Unseen NAS benchmark [16]. It compares the performance of these simple search methods on einspace to several baselines from previous work, including results from DARTS [30] and Bonsai [15] search spaces. The table highlights that einspace’s expressiveness allows it to achieve competitive results even with simple search strategies, and in some cases outperforms a previously reported CFG-based search space (hNASBench201 [46]). The table also indicates the best and second-best performing architecture for each dataset.
read the caption
Table 1: Accuracies resulting from the combination of einspace with the simple search strategies of random sampling, random search, and regularised evolution (RE). See text for further detail. We evaluate performance across multiple datasets and modalities from Unseen NAS [16]. Results transcribed from [16] are denoted *, where DARTS [30] and Bonsai [15] search spaces are employed. The expressiveness of einspace enables performance that remains competitive with significantly more elaborate search strategies, as well as outperforming the CFG-based space hNASBench201 [46] when using evolutionary search in both spaces. Best and second best performance per dataset.

🔼 This table presents the 0-1 error results for CIFAR-10 using three different approaches: a baseline ResNet18 model (RN18), regularized evolution initialized with ResNet18 (RE(RN18)), and regularized evolution initialized with a mix of architectures (RE(Mix)). The lower the 0-1 error, the better the performance. The table highlights the performance improvement achieved by the evolutionary search methods, especially RE(RN18), over the baseline ResNet18 model.
read the caption
Table 8: Lower is better. Performance on CIFAR10 as measured by the 0-1 error.

🔼 This table compares the runtime and number of parameters of the architectures found by different neural architecture search (NAS) methods on eight datasets from the Unseen NAS benchmark [16]. The methods compared are DrNAS, PC-DARTS, regularized evolution (RE) on hNASBench201, and RE on einspace (using a mix of existing architectures as initialization). The table highlights the trade-off between search efficiency (runtime) and model complexity (number of parameters) across different NAS approaches and datasets. Note that some PC-DARTS runtimes are missing because the authors of [16] did not make the logs available.
read the caption
Table 9: Runtime of search algorithms, as well as the number of model parameters for the found architectures. Numbers for PC-DARTS on two datasets are missing due to missing logs from the authors of [16]. RE on einspace is the RE(Mix) variant, while RE on hNASBench201 searches from scratch.

🔼 This table presents the results of three different search strategies (random sampling, random search, and regularized evolution) applied to the einspace search space on various datasets from the Unseen NAS benchmark. It compares the performance of einspace to several baselines, highlighting the impact of the search strategy and the expressiveness of the search space. The table also includes comparative results from other neural architecture search spaces (DARTS and Bonsai) for context.
read the caption
Table 1: Accuracies resulting from the combination of einspace with the simple search strategies of random sampling, random search, and regularised evolution (RE). See text for further detail. We evaluate performance across multiple datasets and modalities from Unseen NAS [16]. Results transcribed from [16] are denoted *, where DARTS [30] and Bonsai [15] search spaces are employed. The expressiveness of einspace enables performance that remains competitive with significantly more elaborate search strategies, as well as outperforming the CFG-based space hNASBench201 [46] when using evolutionary search in both spaces. Best and second best performance per dataset.
Full paper#