TL;DR#
Continual learning, where models learn new tasks without forgetting previous ones, is a significant challenge. Existing methods often struggle with semi-supervised scenarios (using both labeled and unlabeled data), especially when dealing with noisy or inaccurate information. The problem is further complicated by the issue of catastrophic forgetting, where learning a new task causes the model to ‘forget’ previously learned ones.
This paper introduces a novel approach called Persistence Homology Distillation (PsHD) to address these challenges. PsHD leverages topological data analysis, a field of mathematics that studies shapes and their properties, to capture the underlying structure of the data. This allows the model to learn new information without losing information from previous tasks, even if the data is noisy. PsHD shows improved stability and outperforms existing methods across various benchmark datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in continual learning because it tackles the challenge of catastrophic forgetting using unlabeled data. Its novel persistence homology distillation method provides enhanced stability and outperforms existing techniques, offering a significant advancement in semi-supervised continual learning. This opens exciting avenues for future research into robust and efficient continual learning algorithms.
Visual Insights#
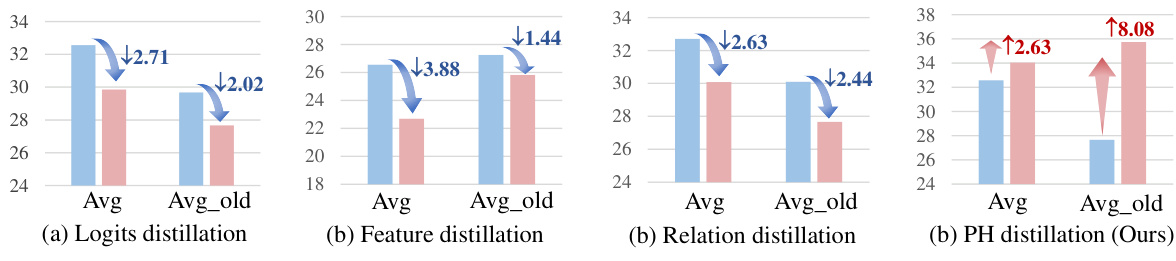
🔼 This figure shows the impact of using extra unlabeled data for distillation in semi-supervised continual learning. Four different methods are compared: iCaRL, PodNet, R-DFCIL, and the authors’ proposed Persistence Homology Distillation (PsHD). The performance is measured by the average incremental accuracy across all tasks (Avg) and the average accuracy on previously learned tasks (Avg_old). The results highlight how PsHD mitigates the negative impact of noisy or inaccurate information in unlabeled data, unlike other methods.
read the caption
Figure 1: The performance interference of extra unlabeled data distillation. The four approaches are (a) iCaRL, (b) PodNet, (c) R-DFCIL and (d) our persistence homology distillation methods. Avg and Avg_old mean the average incremental accuracy of all tasks and old tasks, respectively.
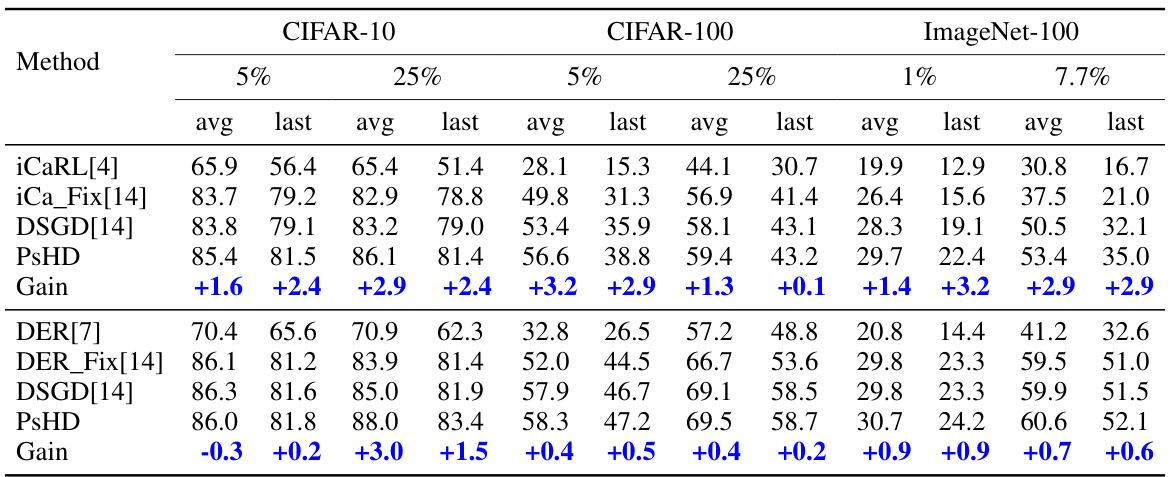
🔼 This table presents the average incremental accuracy and average accuracy for different continual learning methods (iCaRL, iCaRL with Fixmatch, DSGD, DSGD with Fixmatch, DER, DER with Fixmatch and PsHD) across three benchmark datasets (CIFAR-10, CIFAR-100, and ImageNet-100) under different numbers of labeled samples. The results are shown for different percentages of labeled data and highlight the improvements achieved by the proposed PsHD method compared to the state-of-the-art. A memory buffer size of 2000 samples is used.
read the caption
Table 1: Average incremental accuracy and average accuracy of various methods on 5-tasks CIFAR-10, 10-tasks CIFAR-100 and 10-tasks ImageNet-100 settings following the learning sequence [14], with a memory buffer size of 2000. The improvements of PsHD compared to the state-of-the-art methods are highlighted in blue color.
In-depth insights#
Topological Features#
The concept of “Topological Features” in a research paper likely refers to the use of topological data analysis (TDA) to extract meaningful characteristics from complex datasets. TDA focuses on shape and structure rather than raw numerical values, offering robustness to noise and variations. These features may be represented as persistent homology barcodes or diagrams, capturing the evolution of topological structures across different scales. The key advantage lies in TDA’s ability to reveal high-level, global properties, which might be missed by traditional methods relying solely on local patterns. Successful applications often involve using these features for tasks such as classification, clustering, or anomaly detection, where the underlying shape of the data is crucial for accurate modeling. The paper likely explores how these topological features provide improved performance or robustness compared to standard feature extraction techniques, particularly in settings with high-dimensional data, noise, or structural changes.
PsHD Distillation#
The proposed PsHD (Persistence Homology Distillation) method tackles the challenge of catastrophic forgetting and noise sensitivity in semi-supervised continual learning. PsHD leverages persistence homology to extract multi-scale topological features from data, which are inherently robust to noise and variations in data representation. Unlike traditional distillation methods focusing on sample-wise or pairwise similarities, PsHD captures intrinsic structural information, leading to improved stability across tasks. An acceleration algorithm is incorporated to mitigate the computational cost associated with persistence homology calculations. The effectiveness of PsHD is demonstrated through experiments on various datasets and comparisons with state-of-the-art methods, showing significant improvements in accuracy and stability, even with reduced memory buffer sizes. This highlights PsHD’s potential as a powerful technique for robust and efficient semi-supervised continual learning.
SSCL Stability#
Analyzing the stability of Semi-Supervised Continual Learning (SSCL) methods is crucial because continual learning inherently faces catastrophic forgetting. SSCL stability hinges on the ability of a model to learn new tasks without significantly impairing performance on previously learned ones. Factors affecting stability include the chosen model architecture, the distillation method used to preserve old knowledge, the effectiveness of regularization techniques, and the interplay between labeled and unlabeled data. A robust SSCL method should exhibit resilience to noise in the unlabeled data and maintain consistent performance across tasks, even under significant changes in data distribution. This stability analysis should be conducted thoroughly through theoretical analysis (e.g., stability bounds) and comprehensive empirical evaluation on diverse datasets and learning scenarios. Understanding what specific techniques lead to greater stability, especially in the presence of noise, is essential for advancing SSCL research and building more practical continual learning systems.
Computational Cost#
Analyzing the computational cost of persistence homology in the context of semi-supervised continual learning reveals a significant challenge. Standard persistent homology computation scales poorly with data size, making its direct application to large datasets impractical. The authors acknowledge this limitation and propose an acceleration algorithm to mitigate this issue. Their approach involves grouping nearby samples with similar topological structures, computing local persistence diagrams only for these groups, and using these to approximate the overall topological features. This strategy significantly reduces the computational burden, although the precise extent of the improvement and its scalability to even larger datasets require further investigation. The efficiency of the acceleration method is crucial for the practical application of the proposed framework, particularly in scenarios with substantial amounts of unlabeled data. Further research should analyze the trade-off between computational cost reduction and the accuracy of topological feature representation achieved by this approximation.
Future of PsHD#
The future of Persistence Homology Distillation (PsHD) appears bright, given its demonstrated success in semi-supervised continual learning. PsHD’s inherent robustness to noise and its ability to preserve intrinsic structural information offer significant advantages over existing methods. Future research could explore several avenues: extending PsHD to more complex data modalities beyond images, such as text, time series, or point clouds, adapting the simplicial complex construction for these diverse data types. Improving the computational efficiency of PsHD is another crucial area, perhaps through further algorithmic optimizations or the incorporation of hardware acceleration. Investigating the theoretical properties of PsHD more thoroughly, including its generalization capabilities and sensitivity to different types of noise, would strengthen its foundation. Finally, exploring the synergy between PsHD and other continual learning techniques like generative replay or regularization methods could lead to even more powerful and stable continual learning models. By addressing these areas, PsHD could become a leading technique for handling real-world continual learning problems, which often involve high-dimensional, noisy data streams.
More visual insights#
More on figures

🔼 This figure illustrates the process of topological data analysis using persistence homology. (a) shows a filtration of a simplicial complex, where points are gradually connected to form higher-dimensional simplices as a threshold parameter increases. (b) displays the persistence barcode, which represents the lifespan of topological features (connected components, loops, voids, etc.) across different scales. Each bar corresponds to a topological feature, with its length indicating its persistence. Features with longer lifespans are considered more significant. (c) shows the persistence diagram, which is a scatter plot of the birth and death times of topological features. Points close to the diagonal represent short-lived features (noise), while points far from the diagonal signify persistent features (structural information).
read the caption
Figure 2: Illustration of topological data analysis. (a) Filtration of simplicial complex, (b) corresponding persistence barcode, and (c) persistence diagram.
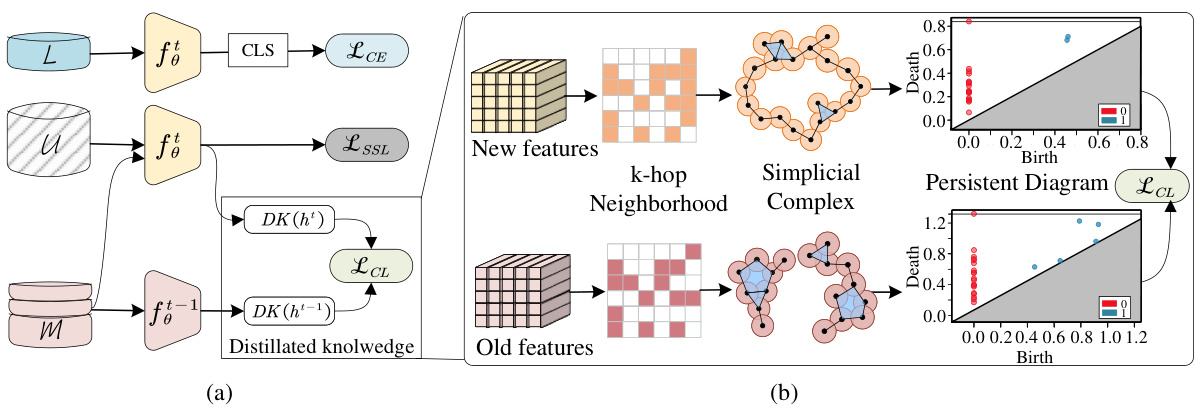
🔼 This figure illustrates the proposed persistence homology distillation (PsHD) method for semi-supervised continual learning. Panel (a) shows the overall architecture, highlighting the cross-entropy loss (LCE) for labeled data, the semi-supervised loss (LSSL) for unlabeled data, and the continual learning loss (LCL) based on the memory buffer. Panel (b) focuses on the PsHD loss (LCL), which uses persistence homology to capture the topological structure of both new and old features, creating a more robust and stable learning process that is less sensitive to noise.
read the caption
Figure 3: Illustration of our proposed persistence homology distillation for semi-supervised continual learning. (a) represents the backbone of SSCL, LCE and LSSL are the cross-entropy loss on labeled data and semi-supervised loss on unlabeled data. LCL means the continual learning loss on the memory buffer. (b) corresponds to our PsHD loss, serving as LCL, employed on the replied samples.
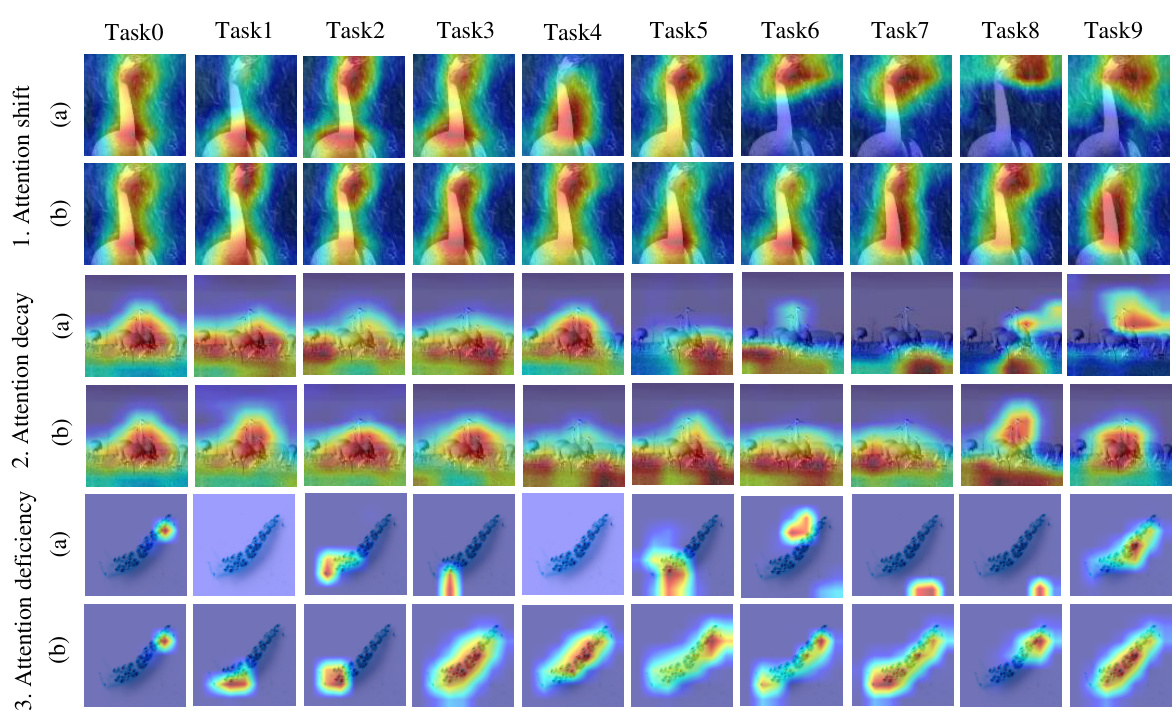
🔼 This figure visualizes the activation heatmaps of old categories during continual learning with and without persistence homology distillation. It shows how the model’s attention to relevant image regions changes across tasks. The (a) columns represent results without the proposed distillation method (PsHD), while (b) columns showcase the results with PsHD. The color intensity indicates the level of activation; redder areas highlight regions of higher activation, indicating stronger attention. The figure demonstrates the positive impact of the PsHD method on preserving the focus on relevant features across tasks, preventing catastrophic forgetting.
read the caption
Figure 4: Visualization of activation heatmap during the continual learning process, where the categories belong to Task0. 1-3(a) correspondence to PsHD without the Lhd, and 1-3(b) correspondence to PsHD with Lhd. The red area localizes class-specific discriminative regions.

🔼 This figure visualizes the impact of the hyperparameter λ (lambda) and the choice of considering 0-dimensional holes (H0) or both 0 and 1-dimensional holes (H01) on the performance of the proposed persistence homology distillation method across three datasets: CIFAR-10, CIFAR-100, and ImageNet-100. For each dataset and setting, it shows the average incremental accuracy (Avg↑) and backward transfer (BWT↓) as a function of λ. The goal is to demonstrate the model’s robustness to noise and the effectiveness of different topological feature representations.
read the caption
Figure 5: Effectiveness of h-simplex features in persistent homology. H0_Avg and H01_Avg represent the average incremental accuracy based on considering 0-dimensional holes and 0,1-dimensional holes persistence. BWT evaluates the forgetting degree.

🔼 This figure visualizes the activation heatmaps of old categories during continual learning with and without the proposed persistence homology distillation (PsHD). The top row shows the results without PsHD, while the bottom row uses PsHD. Each column represents a task in the continual learning process. The heatmaps highlight the regions of the image that are most important for classification, allowing for a visual comparison of how effectively each method maintains focus on relevant features across tasks. The redder areas indicate stronger activations.
read the caption
Figure 4: Visualization of activation heatmap during the continual learning process, where the categories belong to Task0. 1-3(a) correspondence to PsHD without the Lhd, and 1-3(b) correspondence to PsHD with Lhd. The red area localizes class-specific discriminative regions.
More on tables
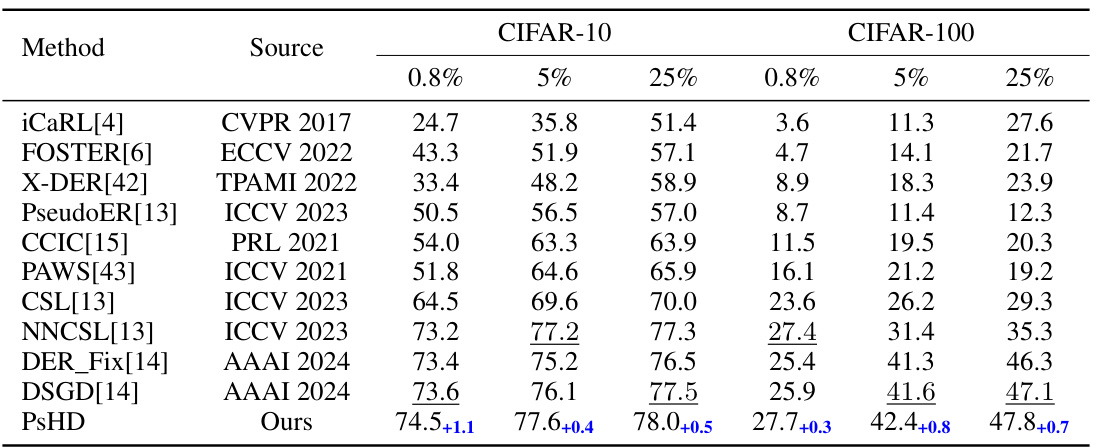
🔼 This table presents the average accuracy and standard deviation of various methods on CIFAR-10 and CIFAR-100 datasets under different supervision levels (0.8%, 5%, 25%). The learning sequence follows the NNCSL method [13], and the memory buffer size is set to 500. The best-performing method in each setting is underlined.
read the caption
Table 2: Average accuracy with the standard derivation of different methods test with 5-tasks CIFAR-10 and 10-tasks CIFAR-100 settings following learning sequence of [13] with 500 samples replayed. The data with underline is the best performance within existing methods.
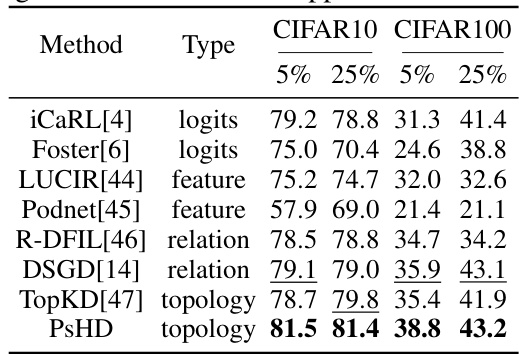
🔼 This table compares the average accuracy of various knowledge distillation methods (logits, feature, relation, and topology distillation) on two datasets (CIFAR-10 and CIFAR-100) with different labeling ratios (5% and 25%). The results demonstrate the effectiveness of different distillation methods in semi-supervised continual learning and highlight the performance of PsHD (Persistence Homology Distillation), a novel topology-based method, which achieves the highest accuracy across all settings. This showcases the benefit of leveraging intrinsic topological features for robust knowledge preservation in continual learning.
read the caption
Table 3: Average accuracy of different knowledge distillation methods applied on SSCL.

🔼 This table presents a comparison of the stability of different distillation methods (Podnet, LUCIR, R-DFCIL, DSGD, TopKD, and PsHD) under different levels of Gaussian noise (σ = 0.2, 1.0, 1.2). For each method and noise level, the table shows the Backward Transfer (BWT) and Average Accuracy (AA↑). BWT indicates the degree of forgetting (a negative value means less forgetting). AA↑ is the average accuracy. The results demonstrate the relative robustness of each method to noise interference.
read the caption
Table 4: Comparison of distillation methods with Gaussian noise interference on CIFAR10 with 5% supervision. σ is the standard deviation.

🔼 This table presents the ablation study of the proposed persistence homology distillation method. It shows the average and last accuracy on CIFAR-10 and CIFAR-100 datasets with 5% and 25% label ratios, respectively. The results are compared for different configurations: using only semi-supervised loss (LSSL), using only persistence homology distillation loss (Lhd), and using both losses. The improvements achieved by adding the proposed Lhd loss are highlighted, demonstrating its effectiveness in enhancing the overall performance.
read the caption
Table 5: Ablation study of proposed persistence homology distillation

🔼 This table shows the average accuracy of different methods with varying percentages of labeled data in the memory buffer. The results demonstrate the impact of the labeled data ratio on model performance in semi-supervised continual learning. It shows how the proportion of labeled vs. unlabeled data in the memory buffer influences the overall accuracy of the model.
read the caption
Table 6: Effect of data allocation in memory buffer

🔼 This table presents the average accuracy results of different continual learning methods on CIFAR-10 and CIFAR-100 datasets under various label ratios (0.8%, 5%, and 25%). The methods compared include PseudoER, CCIC, CSL, NNCSL, and the proposed PsHD. The table also shows the results when the memory buffer size is reduced to 2000 (PsHD*). The results demonstrate the performance improvements of PsHD, especially its memory efficiency when the buffer size is reduced. The learning sequence follows [13].
read the caption
Table 7: Average accuracy of different methods following learning sequence of [13] with memory buffer size 5120. * represents that the size of memory buffer is 2000.

🔼 This table presents a comparison of the average incremental accuracy and average accuracy achieved by different continual learning methods on three benchmark datasets: CIFAR-10, CIFAR-100, and ImageNet-100. The results are presented for different label ratios (5%, 25% for CIFAR-10/100, and 1%, 7.7% for ImageNet-100) and reflect performance after 5, 10 and 10 tasks, respectively. The table highlights the improvement obtained by the proposed PsHD method compared to the state-of-the-art.
read the caption
Table 1: Average incremental accuracy and average accuracy of various methods on 5-tasks CIFAR-10, 10-tasks CIFAR-100 and 10-tasks ImageNet-100 settings following the learning sequence [14], with a memory buffer size of 2000. The improvements of PsHD compared to the state-of-the-art methods are highlighted in blue color.

🔼 This table compares the average accuracy of different methods for semi-supervised continual learning using a memory buffer of size 5120. It shows the average accuracy across six different experimental settings (different datasets and labeling ratios). The table also includes results with a smaller memory buffer (2000), demonstrating the memory efficiency of PsHD. The methods compared include several state-of-the-art methods, such as NNCSL, DER_Fix, and DSGD, along with the proposed PsHD method.
read the caption
Table 7: Average accuracy of different methods following learning sequence of [13] with memory buffer size 5120. * represents that the size of memory buffer is 2000.
Full paper#



















