↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Solving partial differential equations (PDEs) using neural networks is an active research area. Fourier Neural Operators (FNOs) are a promising approach due to their computational efficiency and ability to capture long-range dependencies. However, a lack of theoretical understanding hinders the reliable training and optimization of deep FNOs. Training instability and difficulty in achieving optimal performance are significant obstacles.
This paper introduces a mean-field theory for FNOs, providing a theoretical framework to analyze their behavior. By examining the ordered-chaos phase transition, the researchers established a connection between the FNO’s expressivity and its trainability. They found that the ordered and chaotic phases correspond to vanishing and exploding gradients, respectively. This crucial finding informs practical initialization strategies for stable FNO training and provides valuable insights into the limitations and potentials of FNOs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with Fourier Neural Operators (FNOs). It offers a much-needed theoretical foundation for understanding FNO expressivity and trainability, addressing existing issues of instability and providing practical initialization guidelines. This work directly impacts current research trends in solving PDEs with neural networks and opens avenues for improving FNO performance and design.
Visual Insights#

This figure illustrates the ordered-chaos phase transition in a Fourier Neural Operator (FNO) based on the weight initialization parameter (σ2). The left side shows the ordered phase where, during forward propagation, spatial hidden representations (H(l)) converge to a uniform state, leading to vanishing gradients during backpropagation. Conversely, the right side depicts the chaotic phase, where representations either converge to distinct states or diverge, resulting in exploding gradients. The transition point between these phases is identified as ’the edge of chaos'.
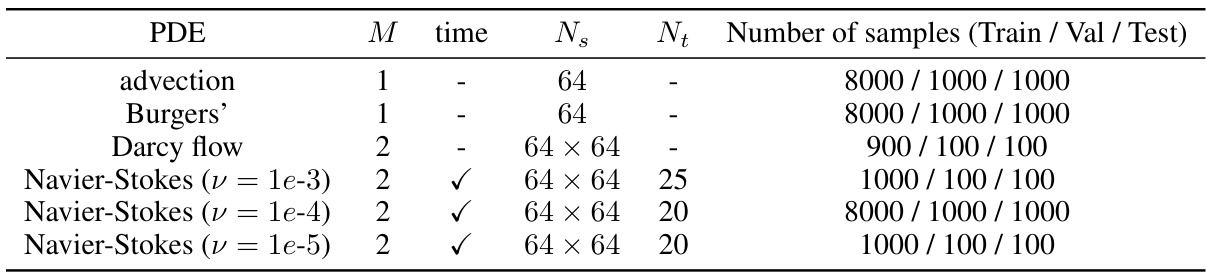
This table summarizes the characteristics of the datasets used in the paper’s experiments. It lists the number of spatial dimensions (M), whether the data is time-dependent, the spatial resolution (Ns), the temporal resolution (Nt) if applicable, and the number of samples used for training, validation, and testing for each dataset (advection, Burgers’, Darcy flow, and Navier-Stokes equations at different viscosities).
In-depth insights#
FNO Mean-Field Theory#
The heading ‘FNO Mean-Field Theory’ suggests a theoretical investigation into the behavior of Fourier Neural Operators (FNOs). A mean-field approach simplifies the analysis of complex systems by considering the average behavior of a large number of interacting units. In the context of FNOs, this might involve analyzing the propagation of information through the network by examining the average activation patterns across many neurons. This approach is particularly useful when analyzing deep FNOs, where traditional methods become computationally intractable. The theory may uncover insights into the FNO’s expressivity and trainability. Understanding phase transitions (ordered-chaotic) is vital as it can explain phenomena like vanishing or exploding gradients, impacting the learning process. A connection between expressivity and trainability could be uncovered, offering guidance on optimal network architectures and initialization strategies for stable training. Overall, the ‘FNO Mean-Field Theory’ would provide a powerful framework to understand and improve FNOs for solving partial differential equations.
Expressivity & Trainability#
The concepts of “Expressivity and Trainability” in the context of neural networks, particularly Fourier Neural Operators (FNOs), are deeply intertwined. Expressivity refers to the network’s capacity to represent complex functions, while trainability focuses on how easily and stably the network’s parameters can be learned. The research likely explores how the network’s architecture, particularly the Fourier transform component and weight initialization, affects both of these characteristics. A key finding might be a connection between the network’s behavior (ordered or chaotic) and its trainability. An ordered phase may correspond to vanishing gradients, preventing effective learning. Conversely, a chaotic phase might lead to exploding gradients, resulting in instability. The optimal region for training likely lies at the ’edge of chaos,’ a transition between these two phases. The analysis may leverage mean-field theory to analyze infinite-width networks, providing a theoretical framework to understand the network’s behavior and guide initialization strategies for more stable and effective training.
Edge-of-Chaos Init#
The concept of “Edge-of-Chaos Init” in the context of neural networks, particularly Fourier Neural Operators (FNOs), centers on initializing network weights to operate at the critical point between ordered and chaotic regimes. An ordered regime implies vanishing gradients, hindering training, while a chaotic regime leads to exploding gradients, also detrimental to learning. The edge of chaos represents a sweet spot where gradients neither vanish nor explode, enabling efficient training. This initialization strategy leverages mean-field theory to analyze the network’s behavior, linking expressivity (how well the network distinguishes between inputs) and trainability. The optimal initialization allows for a balance between these factors. Finding the precise edge-of-chaos setting can depend on factors like network architecture, activation functions, and dataset characteristics, necessitating further research to generalize this approach effectively. Empirical results often demonstrate that initializing near this critical point is crucial for stable and effective FNO training across various PDE problems.
PDE Benchmarks#
A dedicated section on PDE benchmarks in a research paper would be invaluable. It should detail the specific partial differential equations (PDEs) used for evaluation, emphasizing their relevance and diversity. Key aspects of each PDE should be described, including dimensionality, linearity/nonlinearity, type (e.g., elliptic, parabolic, hyperbolic), and boundary conditions. The benchmark’s purpose should be clearly stated, whether it’s for comparing different numerical solvers, assessing the performance of machine learning models, or evaluating the scalability of algorithms. Metrics used for comparison (e.g., accuracy, runtime, memory usage) must be carefully defined and justified. Ideally, the benchmarks should include a range of complexities to challenge various approaches. The paper should discuss the availability of datasets and code associated with the benchmarks, aiding reproducibility. The discussion of potential limitations in the chosen benchmarks, including their representativeness of real-world problems, is crucial for establishing the benchmark’s validity. Finally, the benchmark’s long-term goals and maintenance plan should be addressed.
Future Research#
Future research directions stemming from this work could explore extending the mean-field theory to more complex FNO architectures, including those with skip connections or adaptive mechanisms. Investigating the impact of different activation functions beyond ReLU and Tanh on the ordered-chaos phase transition would also be valuable. A key area for future work is developing more robust initialization strategies that reliably place the network at the edge of chaos, potentially using techniques beyond simple Gaussian initialization. Finally, empirical validation on a wider range of PDEs and datasets with varying complexities and dimensionality is crucial to further solidify the theoretical findings. This includes exploring the impact of mode truncation on expressivity and trainability in greater depth.
More visual insights#
More on figures

This figure shows the average gradient norm during backpropagation for several Fourier Neural Operators (FNOs) with different initial weight variance parameters (σ²). The plots illustrate how the gradient norm changes across layers (depth) of the network. The behavior is shown to depend on the initial σ² value, with some showing consistent increase or decrease as the gradient propagates through the network.

This figure shows how the average gradient norm changes during backpropagation in different FNO models with varying initial weight variance (σ²). Each line represents a different initial σ², ranging from 0.5 to 4.0. The x-axis represents the layer number, while the y-axis shows the logarithm of the average gradient norm. The plot demonstrates that the gradient either consistently increases or decreases depending on the initial σ², highlighting the impact of initialization on the training stability of FNOs.

This figure shows the average gradient norm across different layers during backpropagation for various FNO architectures. The initial weight variance (σ²) is varied, and its impact on gradient behavior is observed. The plots illustrate how gradient norms change consistently (either increasing or decreasing) as backpropagation progresses through the layers depending upon the initial weight variance.

This figure illustrates the ordered-chaos phase transition in a Fourier Neural Operator (FNO) based on the weight initialization parameter (σ²). The left side shows the ordered phase where the hidden representations converge uniformly during forward propagation, resulting in vanishing gradients during backpropagation. Conversely, the right side depicts the chaotic phase where representations diverge or converge to distinct states, leading to exploding gradients. This transition highlights the impact of weight initialization on FNO behavior and its implications for training stability.

This figure shows the phase transition diagram for Deep Convolutional Networks (DCNs) with different activation functions (Tanh and ReLU). The diagrams illustrate how the network’s behavior transitions between an ‘ordered’ phase (where representations of different inputs converge) and a ‘chaotic’ phase (where representations diverge). This transition is controlled by the variance of the weight initialization (σ²) and the variance of the bias initialization (στ). The edge of chaos, representing the optimal initialization for training stability, is highlighted. The vanishing and exploding gradients regions are also identified, associated with the ordered and chaotic phases, respectively.
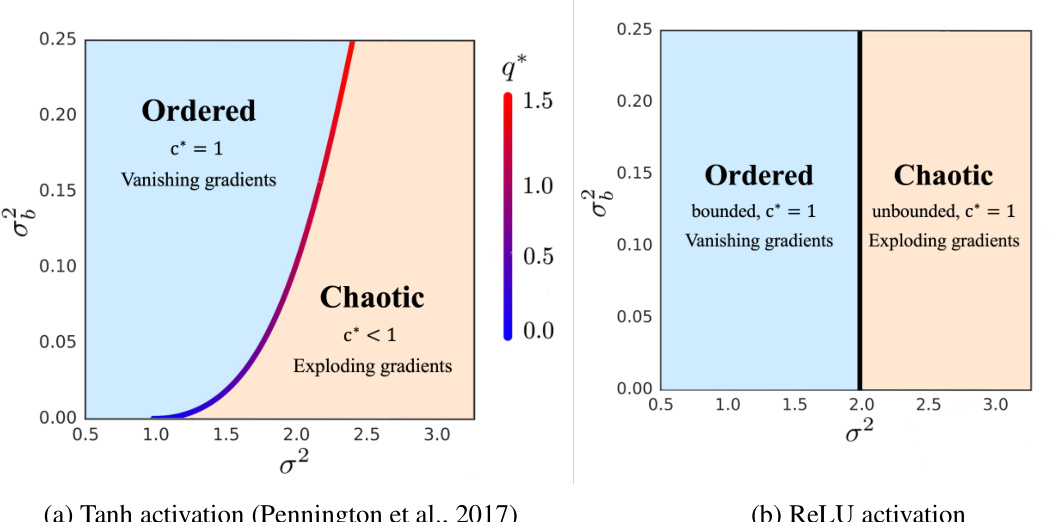
This figure shows the phase transition diagram for Deep Convolutional Neural Networks (DCNNs). The diagrams illustrate the relationship between the initial variance of weights (σ²) and biases (σb²), and the behavior of the network during forward and backward propagation. The left diagram (a) uses the Tanh activation function, while the right diagram (b) uses the ReLU activation function. The x-axis represents σ², and the y-axis represents σb². The color scale indicates the average gradient magnitude. The ordered phase is characterized by vanishing gradients, while the chaotic phase is characterized by exploding gradients. The network is stably trained only at the edge of chaos, the transition point between the ordered and chaotic phases. The key difference between the Tanh and ReLU activations is how the edge of chaos is defined: For Tanh, there is a continuous transition, while for ReLU, the transition is sharp and occurs at a specific value of σ².
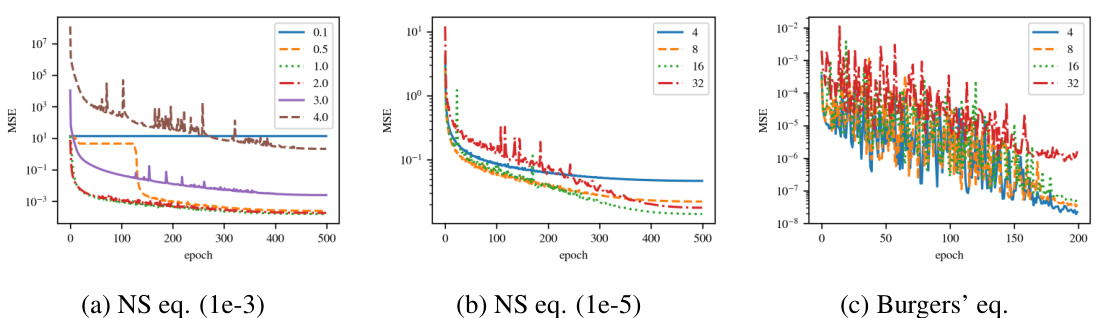
This figure shows the average gradient norm across different layers of several Fourier Neural Operators (FNOs). The initial weight variance (σ²) is varied across several runs, and its impact on the gradient norm over the layers is shown in a log scale. The results show that the gradient norm either consistently increases or decreases, depending on the initial σ² value.

This figure shows the average gradient norm across different layers during backpropagation for various initial weight variances (σ²). It demonstrates how the gradient norm changes as the backpropagation progresses through the network. The plot shows that the gradient either consistently grows (exploding gradients) or shrinks (vanishing gradients) depending on the initial value of σ². The behavior observed provides insights into the stability of FNO training related to initialization.

This figure shows how the average gradient norm changes during backpropagation for different initial values of the weight variance (σ²). The plot demonstrates that the gradient either consistently increases (exploding gradients) or decreases (vanishing gradients) as it propagates through the network’s layers, depending on the initial σ². The behavior is consistent across layers, revealing a relationship between the initial weight variance and gradient stability during training.
This figure illustrates the ordered-chaos phase transition in a Fourier Neural Operator (FNO) as a function of the weight initialization parameter (σ²). The left side shows the ordered phase where spatial representations converge uniformly, leading to vanishing gradients during backpropagation. The right shows the chaotic phase where representations either converge to different states or diverge, resulting in exploding gradients. The transition between these phases highlights a crucial aspect of FNO training stability.

This figure shows how the average gradient norm changes across different layers of several Fourier Neural Operators (FNOs). Each line represents a different initial weight variance (σ²). The x-axis shows the layer number, and the y-axis shows the gradient norm on a logarithmic scale. The plot illustrates that depending on the initial variance, the gradient norm either increases or decreases consistently as backpropagation progresses.

This figure illustrates the ordered-chaos phase transition in a Fourier Neural Operator (FNO) based on the weight initialization parameter (σ²). The left side shows the ‘ordered phase’, where the spatial representations converge uniformly, leading to vanishing gradients during backpropagation. The right side shows the ‘chaotic phase’, resulting in either distinct states or divergence, causing exploding gradients. The transition between these phases is crucial for stable FNO training.
The figure shows how the average gradient norm changes during backpropagation for different FNOs. The initial variance parameter (σ²) is varied, demonstrating its significant impact on gradient behavior. As gradients propagate towards earlier layers, they consistently increase or decrease depending on the initial σ² value, highlighting the importance of appropriate initialization for stable training.

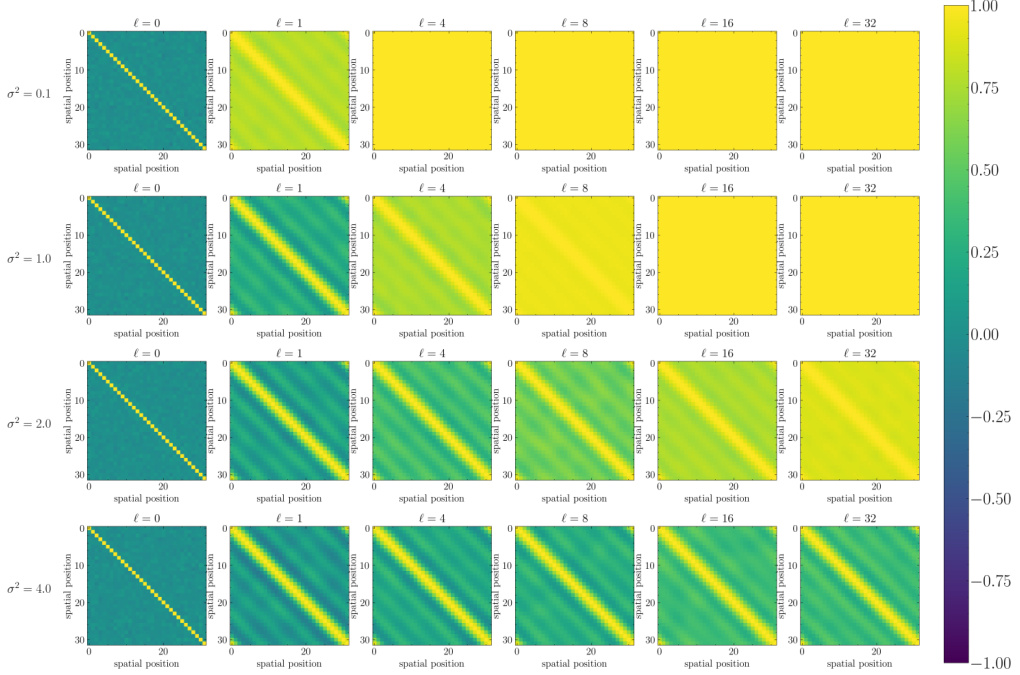
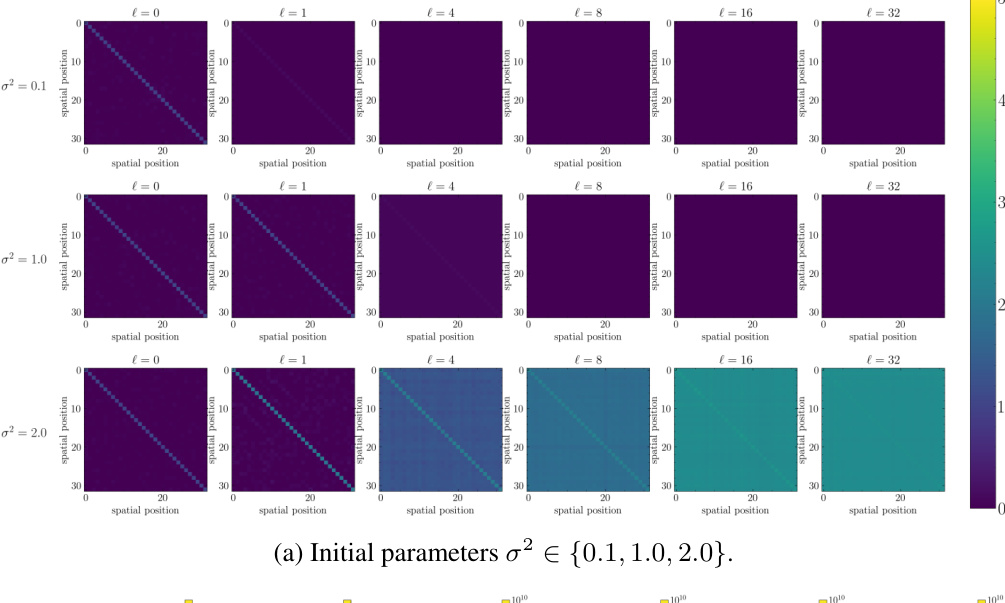
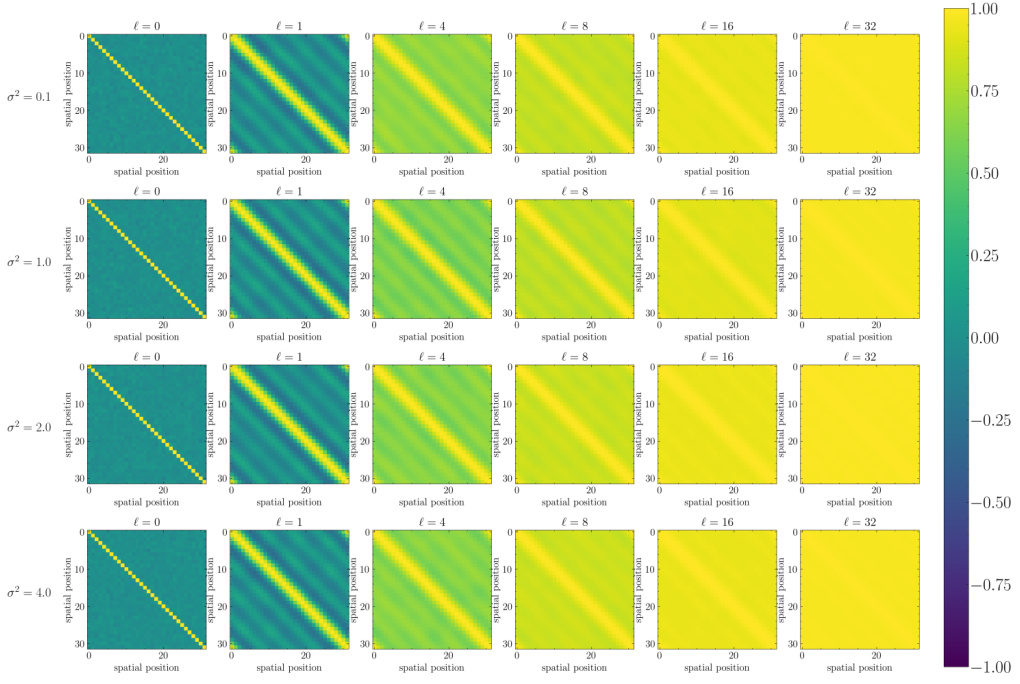
The figure visualizes the correlation of the covariance matrix Σ(l) at different layers (l=0,1,4,8,16,32) of a simplified Fourier Neural Operator (FNO) using the Tanh activation function and without mode truncation. Each subplot represents a layer, showing how the correlation between spatial positions changes during forward propagation. The color scale indicates the strength of the correlation. The pattern shows how the model’s understanding of spatial relationships evolves as it processes the input.
This figure shows the average gradient norm across different layers of several Fourier Neural Operators (FNOs) during backpropagation. The initial weight variance (σ²) is varied, and each line in the plot represents a different σ². The y-axis is a logarithmic scale of the gradient norm, and the x-axis represents the layer number. The plot demonstrates how the gradient norm changes consistently depending on the chosen value of σ² as backpropagation progresses. A consistent increase or decrease in gradient norm is observed depending on σ².

This figure shows the average gradient norm over the depth of several FNOs with different initial weight variances (σ²). The plot shows how the gradient norm changes as backpropagation proceeds through the network layers. The gradient norm either consistently increases (exploding gradients) or decreases (vanishing gradients) depending on the initial σ² value, illustrating the impact of initialization on training stability.
More on tables
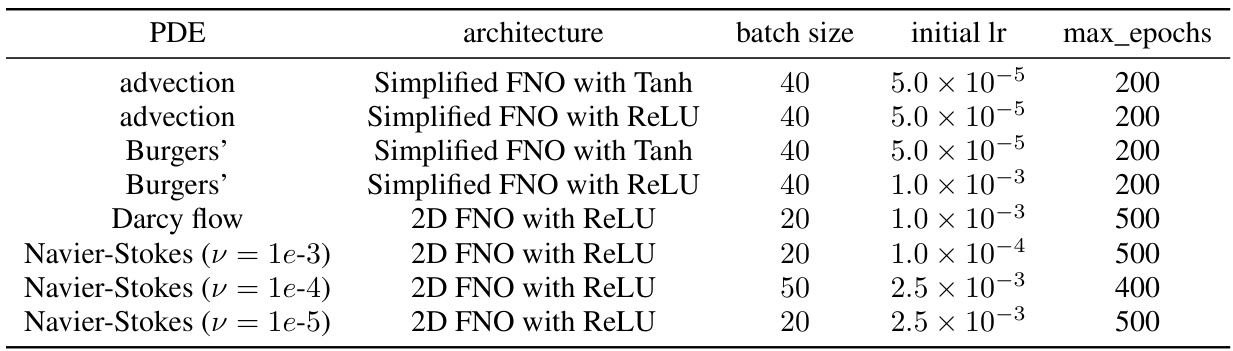
This table shows the training settings used in the experiments described in Section 4 of the paper. It lists the PDE (Partial Differential Equation) solved, the architecture of the Fourier Neural Operator (FNO) used (simplified or 2D, with Tanh or ReLU activation), the batch size, the initial learning rate, and the maximum number of epochs for training. These settings are specific to each experimental configuration and provide crucial details for reproducibility.
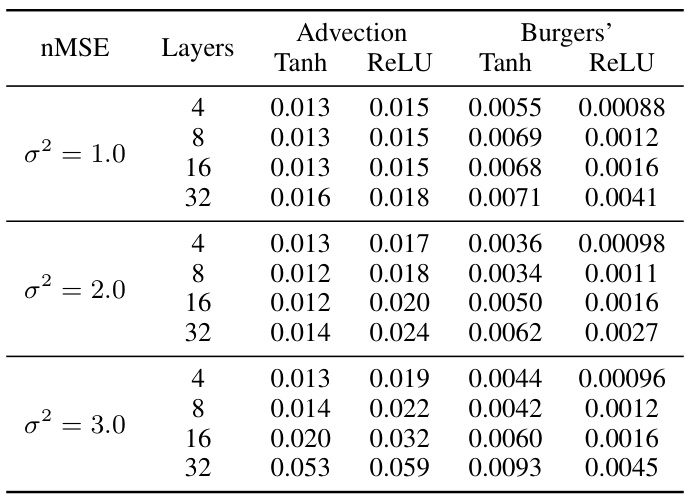
This table presents the test performance (measured by normalized mean squared error, or nMSE) of a simplified 1D Fourier Neural Operator (FNO) on two 1D Partial Differential Equations (PDEs): the advection and Burgers’ equations. The results are broken down by the activation function used (Tanh and ReLU), the number of layers in the FNO (4, 8, 16, and 32), and the initial variance parameter (σ²) which is a key aspect of the paper’s investigation into initialization strategies. Lower nMSE values indicate better performance.

This table shows the normalized mean squared error (nMSE) achieved by a 2D original Fourier Neural Operator (FNO) model using the ReLU activation function on Darcy Flow and Navier-Stokes (NS) equation datasets. The results are broken down by the number of layers in the FNO (4, 8, 16, and 32), and different initial weight variance parameters (σ² = 1.0, 2.0, and 3.0). For NS equation, different viscosity values (v = 1e-3, 1e-4, and 1e-5) are also considered.
Full paper#



















