↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multi-agent imitation learning (MAIL) typically aims to match an expert’s behavior. However, this approach falls short when agents act strategically, deviating from recommendations to maximize their own benefit. The resulting “value gap” metric, while easily minimized, fails to account for this strategic deviation. This paper highlights this inadequacy. The value gap’s focus on matching observed expert behavior is insufficient when agents can deviate based on their individual utility functions and counterfactual scenarios., which causes a large regret gap.
To address this, the paper introduces the “regret gap” as a more robust objective. The regret gap accounts for potential agent deviations by explicitly considering the impact of recommendations outside the observed behavior. The paper proposes two novel algorithms, MALICE and BLADES, that efficiently minimize the regret gap. MALICE relies on an assumption about the expert’s coverage of the state space, while BLADES utilizes a queryable expert. Both achieve theoretically optimal regret gap bounds, demonstrating the feasibility of efficient regret minimization in MAIL. The results highlight the importance of considering strategic agent behavior and using regret as a metric for improved robustness in multi-agent systems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in multi-agent imitation learning because it addresses the limitations of existing methods by focusing on regret minimization instead of just value matching. This shift provides robustness against strategic agents, a critical aspect often overlooked. The proposed algorithms and theoretical analysis open new avenues for developing more effective coordination strategies in various multi-agent systems, pushing the field forward. The efficient reductions provided for minimizing the regret gap, under different assumptions, provide valuable tools for researchers to tackle real-world multi-agent coordination problems.
Visual Insights#

This figure summarizes the relationship between value equivalence and regret equivalence in the context of multi-agent imitation learning (MAIL). It shows that under sufficiently expressive reward functions and agent deviation classes, achieving regret equivalence (where the learner’s policy is as good as the expert’s, even considering strategic agent deviations) implies value equivalence (where the learner’s and expert’s policies have the same value for all agents under obedient behavior). However, the converse is not true; value equivalence does not guarantee regret equivalence. This highlights that regret equivalence is a stronger requirement than value equivalence in MAIL, reflecting the challenge of accounting for strategic agent behavior.

This table summarizes the upper and lower bounds on the regret gap for different multi-agent imitation learning (MAIL) algorithms. The regret gap measures how much better an expert’s policy performs compared to a learner’s policy, even when strategic agents may deviate from recommendations. The table shows bounds for both existing single-agent IL algorithms adapted to the multi-agent setting (J-BC, J-IRL) and the novel algorithms proposed in the paper (MALICE, BLADES). The bounds depend on factors like the horizon (H), recoverability (u), and coverage (β).
In-depth insights#
MAIL Regret Gap#
The concept of a ‘MAIL Regret Gap’ introduces a crucial refinement to multi-agent imitation learning (MAIL). Traditional MAIL focuses on minimizing the value gap, ensuring the learner’s policy performs as well as the expert’s within the observed state distribution. However, this ignores the strategic nature of agents who might deviate if beneficial. The regret gap, in contrast, directly addresses this by quantifying the maximum incentive any agent has to deviate from the learner’s recommendations, considering counterfactual scenarios outside the expert’s demonstrated behavior. This shift highlights a fundamental difference between single-agent and multi-agent IL: achieving value equivalence in MAIL is far easier than achieving regret equivalence, as the latter necessitates understanding agents’ potential reactions to unseen recommendations. The paper explores this distinction and proposes algorithms that address minimizing the regret gap under various assumptions, highlighting the challenge but also suggesting potential solutions to more robust multi-agent learning.
Value vs. Regret#
The core of the “Value vs. Regret” discussion lies in contrasting two fundamental objectives in multi-agent imitation learning (MAIL). Value-based approaches aim to minimize the difference in performance between a learned agent and an expert, focusing on matching observed behavior. However, this ignores strategic agents who might deviate from recommendations if beneficial. Regret-based approaches, conversely, account for such strategic deviations by explicitly considering the potential for agents to exploit the learned policy. While value equivalence is relatively easy to achieve using existing single-agent imitation learning techniques, it provides no guarantee of robustness to strategic deviations; regret equivalence is significantly more challenging, requiring consideration of counterfactual scenarios. The key insight is that focusing solely on value may lead to policies vulnerable to exploitation, highlighting the importance of the regret perspective in truly robust MAIL solutions.
Algorithm Reductions#
The core of this research lies in its novel algorithm reductions that tackle the challenge of multi-agent imitation learning (MAIL). Instead of directly addressing the complexities of MAIL, the authors cleverly reduce the problem to more manageable subproblems. This is achieved by strategically leveraging existing single-agent imitation learning (SAIL) algorithms, adapting them to the multi-agent setting under specific assumptions. Two main reduction strategies are explored: one based on the assumption of full coverage of expert demonstrations and another that grants access to a queryable expert. These reductions are significant because they convert the inherently difficult problem of minimizing the regret gap in MAIL into solving a series of more tractable optimization problems. This approach not only leads to efficient algorithms (MALICE and BLADES) but also provides theoretical guarantees on the regret gap, showcasing the power of reduction techniques in simplifying intricate problems. The theoretical analysis, including upper and lower bounds on the regret gap, demonstrates that the reductions are both effective and theoretically grounded. However, the success of these reductions is contingent upon the validity of their underlying assumptions.
Coverage Assumption#
The ‘Coverage Assumption’ in multi-agent imitation learning (MAIL) is crucial for the success of algorithms aiming to minimize the regret gap. It essentially posits that the expert’s demonstrations adequately cover the state space, meaning there is sufficient data to learn how the expert would respond to arbitrary agent deviations in various situations. This assumption is critical because minimizing the regret gap requires understanding counterfactual situations – those where agents deviate from recommendations, which may not be represented in the expert data. Without coverage, the algorithm might lack training data for critical scenarios, leading to poor generalization when facing strategic agents and high regret. Therefore, this assumption simplifies the complexity of the problem, enabling efficient regret-minimizing algorithms, but simultaneously introduces a limitation in applicability to real-world problems where exhaustive expert demonstrations are rare.
Future of MAIL#
The future of multi-agent imitation learning (MAIL) hinges on addressing its current limitations. Robustness to strategic agents is paramount; current methods often fail when agents deviate from the learned policy, highlighting a need for algorithms that explicitly account for such deviations. Improved efficiency is another key area; current approaches can be computationally expensive and data-hungry. Future research should explore more efficient algorithms, possibly drawing on techniques from online learning and optimization. Addressing the lack of generalizability is also crucial; current methods may perform well on specific tasks or environments but fail to generalize to others. Addressing covariate shift and developing techniques robust to distributional changes are necessary for wider applicability. Finally, incorporating richer models of agent behavior is essential; current approaches often assume simplistic agent models, which limits their effectiveness. More sophisticated models, possibly informed by game theory and behavioral economics, could lead to more accurate and robust learning. Ultimately, the future of MAIL lies in creating algorithms that are robust, efficient, generalizable, and based on more realistic agent models.
More visual insights#
More on figures
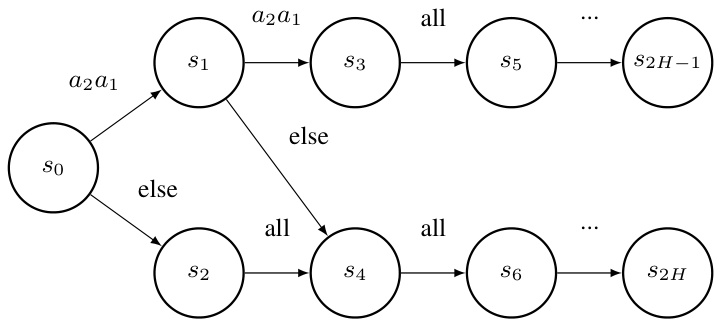
The figure shows a Markov Game where the expert policy only visits states s2, s4,…s2H. However, if an agent deviates from the expert’s recommendation, state s1 becomes reachable. This highlights the challenge of minimizing regret in multi-agent imitation learning, as the learner needs to know what the expert would have done in these unvisited states (counterfactual scenarios).
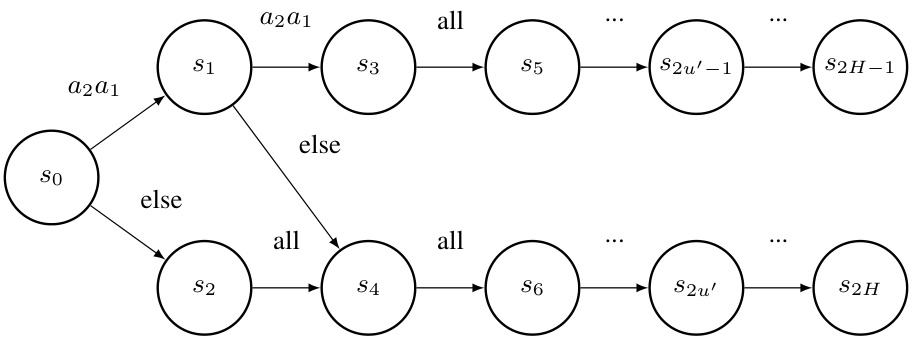
This figure illustrates a Markov game where the regret gap is Ω(ευH) for both J-BC and J-IRL algorithms. The game consists of 2H states arranged in two parallel chains. The expert policy (σε) focuses on one chain, while the learner’s policy (σ) matches it perfectly on the states visited by σε. However, a strategic deviation by an agent creates a counterfactual scenario where the expert’s actions are unknown, resulting in a large regret gap. This highlights that minimizing the value gap does not guarantee minimizing the regret gap in multi-agent scenarios.
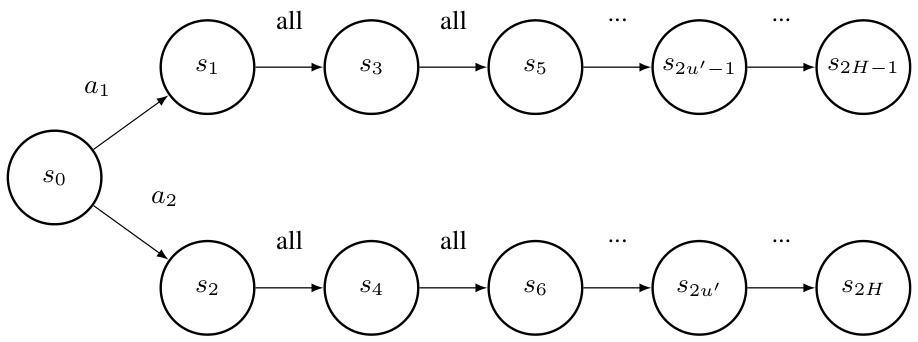
This figure illustrates an example Markov Game demonstrating that the regret gap for both Joint Behavioral Cloning (J-BC) and Joint Inverse Reinforcement Learning (J-IRL) can be as large as Ω(ευH). The figure highlights a scenario where, even with small value gaps, large regret gaps can emerge due to the difference between the expert and learner’s behaviour in states that are not visited under the expert’s policy (but are visited when an agent deviates). This underscores the difficulty of achieving regret equivalence in multi-agent imitation learning.
More on tables

This table summarizes the upper and lower bounds on the regret gap for different multi-agent imitation learning algorithms. The regret gap measures how much better an expert’s policy performs than a learned policy, even when agents are allowed to strategically deviate from recommendations. The algorithms are compared under two different assumptions: (1) a coverage assumption on the expert’s demonstrations (β-coverage) and (2) access to a queryable expert. The bounds are expressed in terms of the horizon (H) of the Markov game, the coverage constant (β), and the recoverability constant (u).

This table summarizes the upper and lower bounds on the regret gap for different multi-agent imitation learning (MAIL) approaches. The regret gap measures the difference in the maximum incentive for an agent to deviate from the learned policy versus the expert policy. The table shows results for four approaches (J-BC, J-IRL, MALICE, BLADES), each under different assumptions (coverage, queryable expert). The bounds are expressed in terms of the horizon (H) of the Markov game, the recoverability constant (u), and the coverage constant (β).
Full paper#



















