TL;DR#
Learning low-dimensional functions from high-dimensional data is a core challenge in machine learning. Existing theoretical analyses, often based on correlational statistical queries, suggested limitations on gradient descent algorithms like SGD. These analyses pointed to a gap between the computationally achievable performance and the information-theoretic limit. This paper focuses on single-index models, a class of functions with low intrinsic dimensionality.
This research demonstrates that SGD, when modified to reuse minibatches, can overcome the limitations highlighted by the correlational statistical query lower bounds. By reusing data, the algorithm implicitly exploits higher-order information beyond simple correlations, achieving a sample complexity close to the information-theoretic limit for polynomial single-index models. This significant improvement is attributed to the algorithm’s ability to implement a full statistical query, rather than just correlational queries. The findings challenge conventional wisdom about SGD’s limitations and suggest new avenues for enhancing learning efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial because it demonstrates that SGD, a widely used algorithm, can learn low-dimensional structures in high-dimensional data more efficiently than previously thought. This challenges existing theoretical understanding and opens new avenues for optimizing neural network training, impacting various machine learning applications.
Visual Insights#
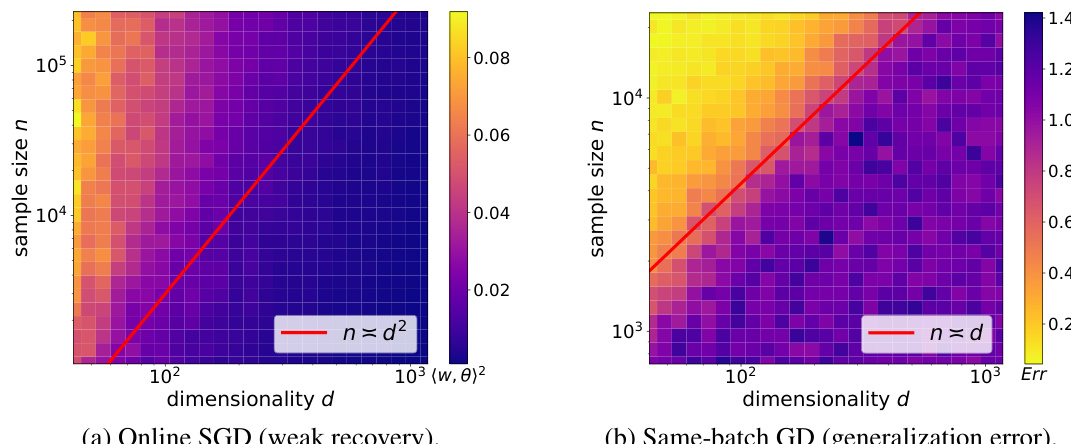
🔼 This figure shows the results of training a two-layer ReLU neural network with 1024 neurons using two different approaches: online SGD with a batch size of 8 and GD on the same batch of size n for 2¹⁴ steps. The target function is f*(x) = H3((x, θ)), where H3 is the third Hermite polynomial. The heatmaps display the weak recovery (overlap between learned parameters w and the target direction θ) for online SGD and the generalization error for GD, averaged over 10 runs. The results highlight a significant difference in performance between the two approaches, with online SGD failing to achieve low test error even with a large number of samples, while GD with batch reuse achieves low generalization error with n ~ d samples.
read the caption
Figure 1: We train a ReLU NN (3.1) with N = 1024 neurons using SGD (squared loss) with step size η = 1/d to learn a single-index target f*(x) = H3((x, θ)); heatmaps are values averaged over 10 runs. (a) online SGD with batch size B = 8; (b) GD on the same batch of size n for T = 214 steps. We only report weak recovery (i.e., overlap between parameters w and target θ, averaged across neurons) for online SGD since the test error does not drop.
Full paper#



















