TL;DR#
3D Gaussian Splatting (3DGS) is widely used for 3D scene reconstruction but lacks uncertainty quantification, hindering its application in robotics and other fields where uncertainty is critical. Existing methods are either computationally expensive or lack accuracy. This necessitates the development of efficient and accurate uncertainty quantification methods.
This paper introduces a novel uncertainty estimation method built upon Bayesian inference. It uses a variational multi-scale approach, constructing diversified parameter space samples by leveraging scale information in 3DGS parameters. An offset table technique efficiently draws these samples. The learned offset posterior quantifies uncertainty for each Gaussian component and improves the rendering quality. Experiments demonstrate superior calibration and rendering compared to previous methods, and the ability to remove noisy Gaussians automatically.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical limitation of 3D Gaussian Splatting (3DGS), a popular technique for 3D scene reconstruction, by introducing a novel method for uncertainty estimation. This is crucial for applications like robotics, where understanding uncertainty is key for safe and reliable navigation. The proposed variational multi-scale approach improves the efficiency and accuracy of uncertainty quantification. It opens new avenues for research into robust and reliable 3D scene reconstruction. The method’s ability to automatically remove noisy data also enhances the quality of reconstructed scenes.
Visual Insights#

🔼 This figure shows the results of applying the proposed uncertainty estimation method to remove noisy Gaussians from a 3D scene reconstructed using 3D Gaussian Splatting (3DGS). By removing Gaussians with high parameter uncertainty (mostly background elements), the model retains a high-fidelity representation of the main object (a desk) even after removing a large percentage of the total Gaussians (up to 90%). This demonstrates the effectiveness of the method in enhancing scene quality by eliminating noise.
read the caption
Figure 1: The results of cleaning up an unbounded scene reconstructed with 3DGS using our uncertainty estimation. We remove the Gaussians with large parameter uncertainty, the majority of which are under-reconstructed background. The desk at the center of the scene remains complete even after removing 90% of the Gaussians.

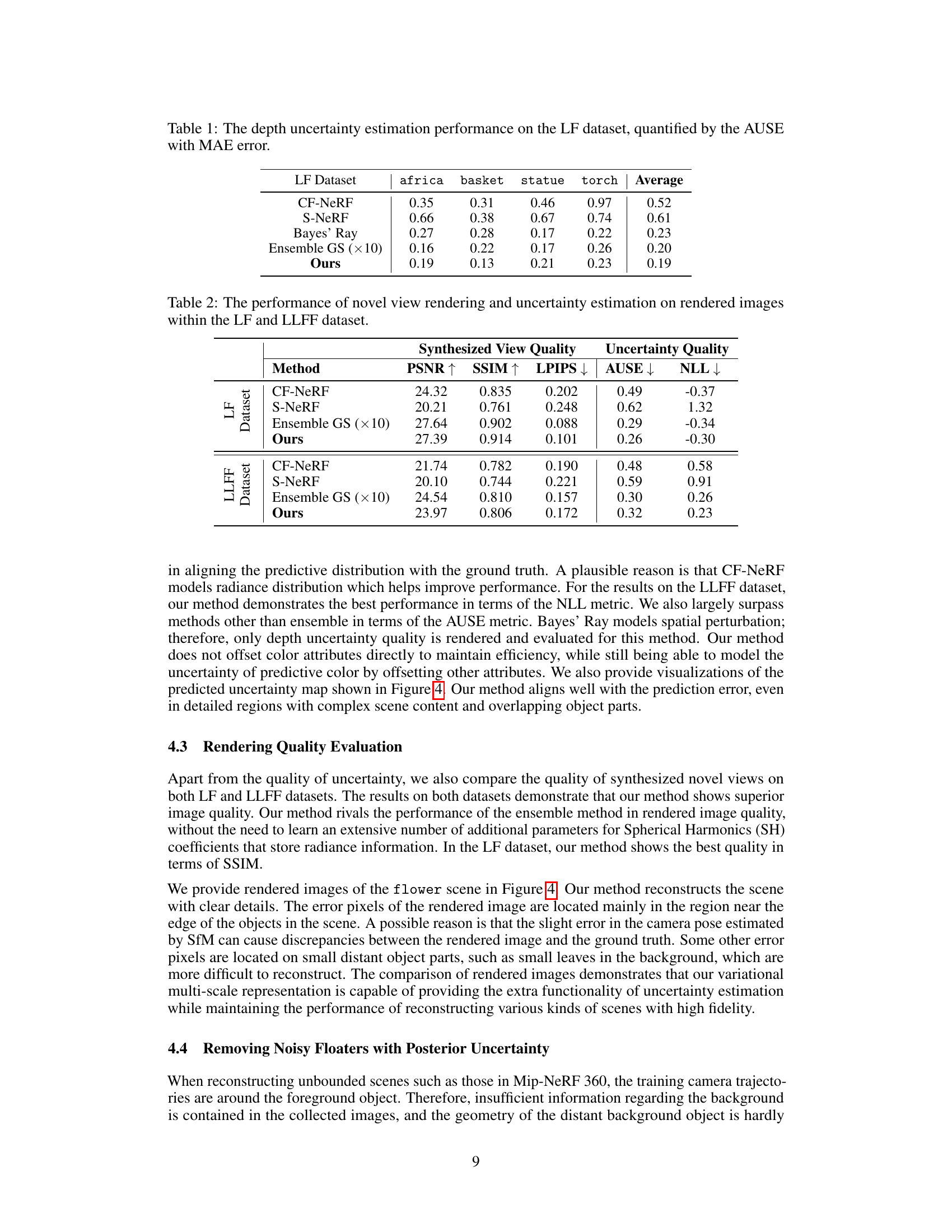
🔼 This table presents a quantitative evaluation of depth uncertainty estimation methods on the LF dataset. The Area Under Sparsification Error (AUSE) metric, combined with Mean Absolute Error (MAE), assesses the alignment between predicted uncertainty and actual error. Lower AUSE values indicate better calibration between predicted uncertainty and the ground truth MAE.
read the caption
Table 1: The depth uncertainty estimation performance on the LF dataset, quantified by the AUSE with MAE error.
In-depth insights#
Multi-scale 3DGS#
The concept of “Multi-scale 3DGS” suggests an enhancement to the standard 3D Gaussian Splatting (3DGS) method. Standard 3DGS represents a scene using a collection of Gaussians, but a multi-scale approach would likely involve representing the scene at multiple levels of detail. This could improve rendering efficiency by using fewer, larger Gaussians for coarser views and progressively more, smaller Gaussians for finer details, similar to techniques used in Level of Detail (LOD) methods. The method’s effectiveness would depend on the efficient handling of these multiple scales. It might involve hierarchical data structures or clever sampling strategies to avoid the computational overhead of managing many Gaussians simultaneously. Another key aspect would be how the multi-scale representation informs uncertainty estimation. Perhaps the uncertainty could be modeled differently at different scales, providing more reliable uncertainty at coarser scales and potentially more granular information at finer scales. The overall benefit would be higher-quality renderings and more accurate uncertainty quantification, especially in complex scenes or when dealing with limited data.
Bayesian Inference#
Bayesian inference provides a powerful framework for quantifying uncertainty in 3D Gaussian Splatting (3DGS) by directly addressing the limitations of traditional MLE approaches. Instead of producing point estimates, Bayesian inference focuses on estimating the full posterior distribution of model parameters, capturing uncertainty due to limited data and model assumptions. This is particularly valuable in applications where uncertainty quantification is crucial, such as robotics and navigation. In the context of 3DGS, Bayesian inference enables the probabilistic modeling of the scene, which is inherently noisy, due to sensor limitations, occlusion and object movement. By incorporating a prior distribution over the model parameters, Bayesian inference regularizes the model and improves robustness against overfitting. This leads to more reliable predictions and uncertainty estimations, enhancing the utility of the 3DGS reconstruction for downstream tasks. Further, variational inference, a key technique within the Bayesian framework, offers a practical approach to approximate the intractable posterior distributions encountered in complex models such as 3DGS. This allows for efficient estimation of uncertainty even with high-dimensional parameter spaces.
Variational Inference#
Variational inference, within the context of this research paper, is presented as a powerful technique to efficiently approximate intractable probability distributions. The core concept revolves around the use of a simpler, tractable distribution (the variational distribution) to approximate the complex, true posterior distribution. The method’s effectiveness hinges on the judicious selection of this variational distribution, which should be flexible enough to capture the essential characteristics of the target distribution but also computationally manageable. The paper leverages this framework to estimate uncertainty in 3D Gaussian splatting by constructing a multi-scale representation. Variational inference allows for the learning of the parameters of the variational distribution via optimization, specifically minimizing the Kullback-Leibler (KL) divergence between the variational and true distributions. This minimization process effectively quantifies the uncertainty associated with each Gaussian component, providing a principled way to identify and remove noisy Gaussians, ultimately enhancing the quality and fidelity of the 3D scene reconstruction. The use of a multi-scale approach further enhances the model’s ability to capture fine details and uncertainty at various scales, thus leading to more robust and accurate results compared to single-scale methods.
Uncertainty Estimation#
The paper proposes a novel uncertainty estimation method for 3D Gaussian Splatting (3DGS), a technique used for real-time 3D scene reconstruction. The core idea is to leverage variational multi-scale inference, creating a diverse set of model parameters by strategically offsetting selected Gaussian attributes. This approach cleverly balances diversity and efficiency in exploring the parameter space, crucial for accurate uncertainty quantification. A key component is the introduction of an offset table, which learns the distribution of these offsets, further enhancing efficiency. The learned posterior distribution then allows for the quantification of uncertainty at both the individual Gaussian and prediction levels. Experimental results demonstrate improved calibration and rendering quality compared to existing methods, showcasing the effectiveness of the proposed multi-scale framework. The application of uncertainty estimates to remove noisy Gaussians, effectively improving scene fidelity, highlights the practical value of the proposed method.
Floater Removal#
The concept of ‘Floater Removal’ in the context of 3D scene reconstruction using Gaussian Splatting is crucial for enhancing visual quality. Floaters, often arising from insufficient data or under-reconstructed background regions, manifest as noisy or blurry artifacts that detract from the overall scene fidelity. The paper proposes a novel uncertainty-aware method to address this problem by leveraging the estimated uncertainty of individual Gaussian components. By identifying and removing Gaussians with high uncertainty, the method effectively cleans up the scene, preserving the high-fidelity parts while eliminating these undesirable artifacts. This approach not only improves the visual appeal but also contributes to the efficiency of the reconstruction process by reducing the number of Gaussians required for representation. The effectiveness of the method is particularly noteworthy in unbounded scenes where the background is often poorly reconstructed, making it a significant contribution to the 3D Gaussian Splatting technique.
More visual insights#
More on figures

🔼 This figure compares three different methods for approximating Bayesian inference in the context of scene representation. (a) Laplace’s Approximation uses a single Gaussian to represent the posterior distribution. (b) Ensemble methods use multiple models to generate a set of samples that cover the posterior distribution. (c) The proposed multi-scale variational inference method leverages explicit scale information in the 3D Gaussian Splatting parameters to efficiently generate diverse samples from the posterior distribution by constructing multi-scale Gaussians. This allows for more efficient and accurate uncertainty estimation.
read the caption
Figure 2: The comparison between our multi-scale variational inference and other methods. (a) Laplace's Approximation fits posterior with normal distribution where the mean equals maximum a posteriori solution θMAP and precision equals fisher information I(θ). (b) The ensemble method learns multiple models simultaneously to form the model space samples. (c) Our method builds a multi-scale representation of the scene, where inference is done by sampling the offset distribution and forming finer Gaussians.

🔼 This figure illustrates the proposed variational multi-scale representation for 3D Gaussian Splatting. It shows how base Gaussians (major scene components) are spawned into multi-scale finer Gaussians. An offset table, learned through variational inference with a multi-scale prior, efficiently controls this spawning process by offsetting a subset of Gaussian attributes. This allows for efficient uncertainty quantification by inferring predictive and parameter uncertainty from the learned offset table.
read the caption
Figure 3: The pipeline of our variational multi-scale representation. We spawn base Gaussians, which are the major components in the scene, into multi-scale finer Gaussians. We learn an offset table to perform the spawn operation by offsetting a subset of attributes. The offset table is learned with variational inference with multi-scale prior. The predictive and parameter uncertainty can be inferred from the variational parameters stored in the table.

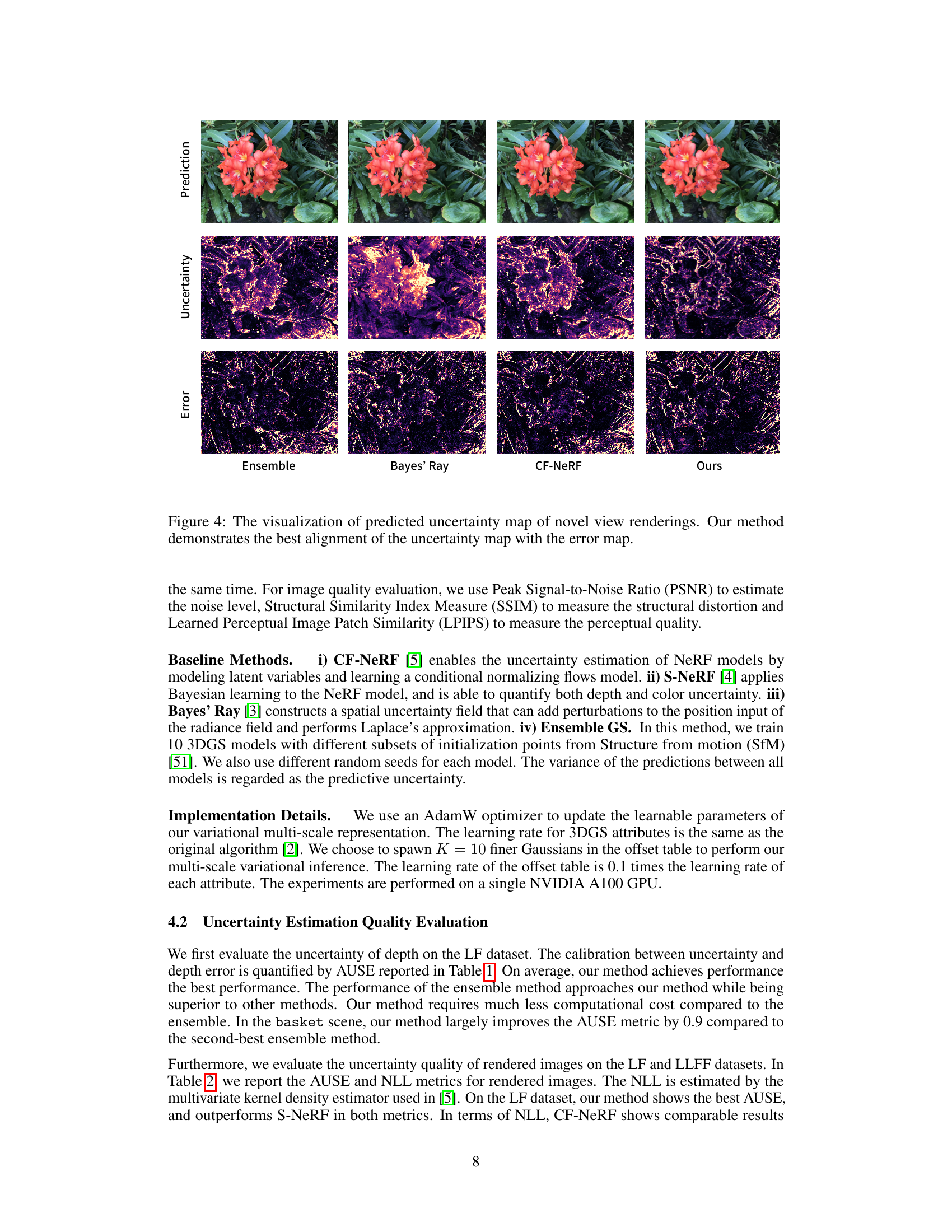
🔼 This figure compares the predicted uncertainty maps of novel view renderings generated by four different methods: Ensemble, Bayes’ Ray, CF-NeRF, and the proposed method. Each method’s uncertainty map is displayed alongside the corresponding error map (difference between prediction and ground truth). The figure visually demonstrates that the proposed method’s uncertainty map most accurately reflects the areas of high error in the rendered image, indicating a superior alignment between estimated uncertainty and actual rendering errors.
read the caption
Figure 4: The visualization of predicted uncertainty map of novel view renderings. Our method demonstrates the best alignment of the uncertainty map with the error map.

🔼 This figure visualizes the results of removing noisy Gaussians from scenes in the Mip-NeRF 360 dataset. By progressively removing Gaussians with high posterior uncertainty (those contributing least to the scene), the algorithm effectively cleans up the reconstructed scene, reducing noise and floaters. The removal process is shown in three stages: 50% Gaussians, 30% Gaussians. The zoomed-in details emphasize that the main objects of interest remain intact and high-quality, despite the significant reduction of Gaussians.
read the caption
Figure 5: The results of noisy Gaussian removal on Mip-NeRF 360 scenes. By gradually deleting the Gaussians with large posterior uncertainty, our method removes the blurred floaters. The object of interest remains complete after the clean-up.
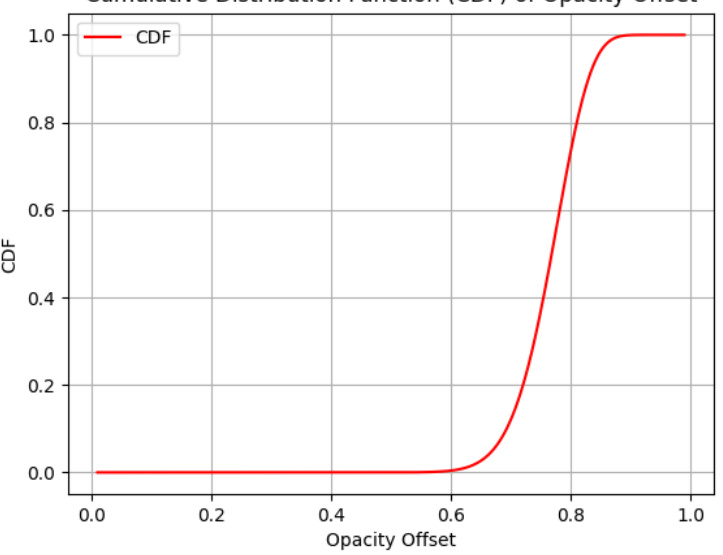
🔼 This figure shows the cumulative distribution function (CDF) of the prior distribution for the opacity offset (χa). The prior is designed to encourage small perturbations to the opacity during variational inference. The CDF demonstrates a high probability of the offset being close to 1, indicating a preference for small increases in opacity. The sigmoid function used to map a normally distributed variable η to χa contributes to the shape of this CDF, ensuring numerical stability during optimization.
read the caption
Figure 6: The Cumulative Distribution Function (CDF) of opacity offset prior.

🔼 This figure shows additional qualitative results of the proposed method on the LLFF dataset. For each scene (Room, Horns, Trex), the ground truth images, rendered images from novel viewpoints, the error maps (difference between the ground truth and rendered images), and the predicted uncertainty maps are shown. The error maps and uncertainty maps are aligned, showing that the uncertainty estimates capture the error well.
read the caption
Figure 7: Addtional visualization results.
More on tables
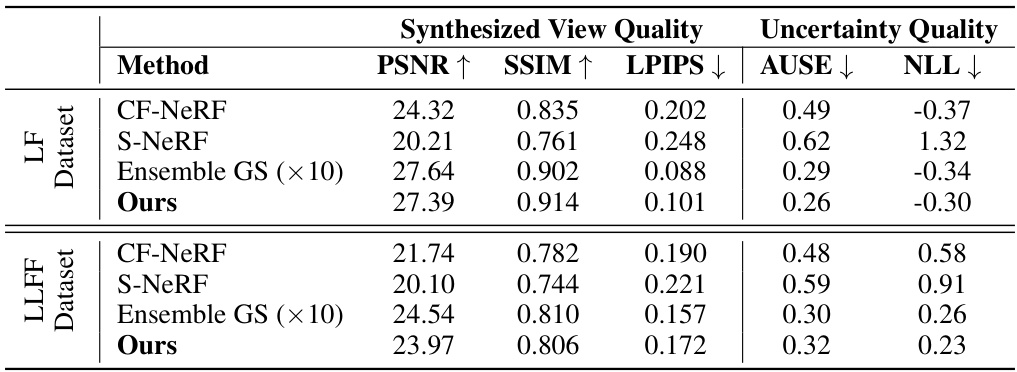
🔼 This table presents a quantitative comparison of the proposed multi-scale variational inference method against several baseline methods for view synthesis and uncertainty estimation. The metrics used include PSNR, SSIM, and LPIPS to evaluate the quality of synthesized novel views, and AUSE and NLL to assess the accuracy and reliability of uncertainty estimations. The results are shown separately for the LF and LLFF datasets, providing a comprehensive evaluation of the method’s performance across different scenes and datasets.
read the caption
Table 2: The performance of novel view rendering and uncertainty estimation on rendered images within the LF and LLFF dataset.
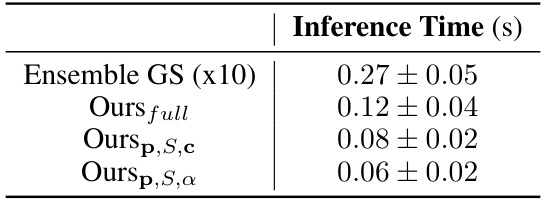
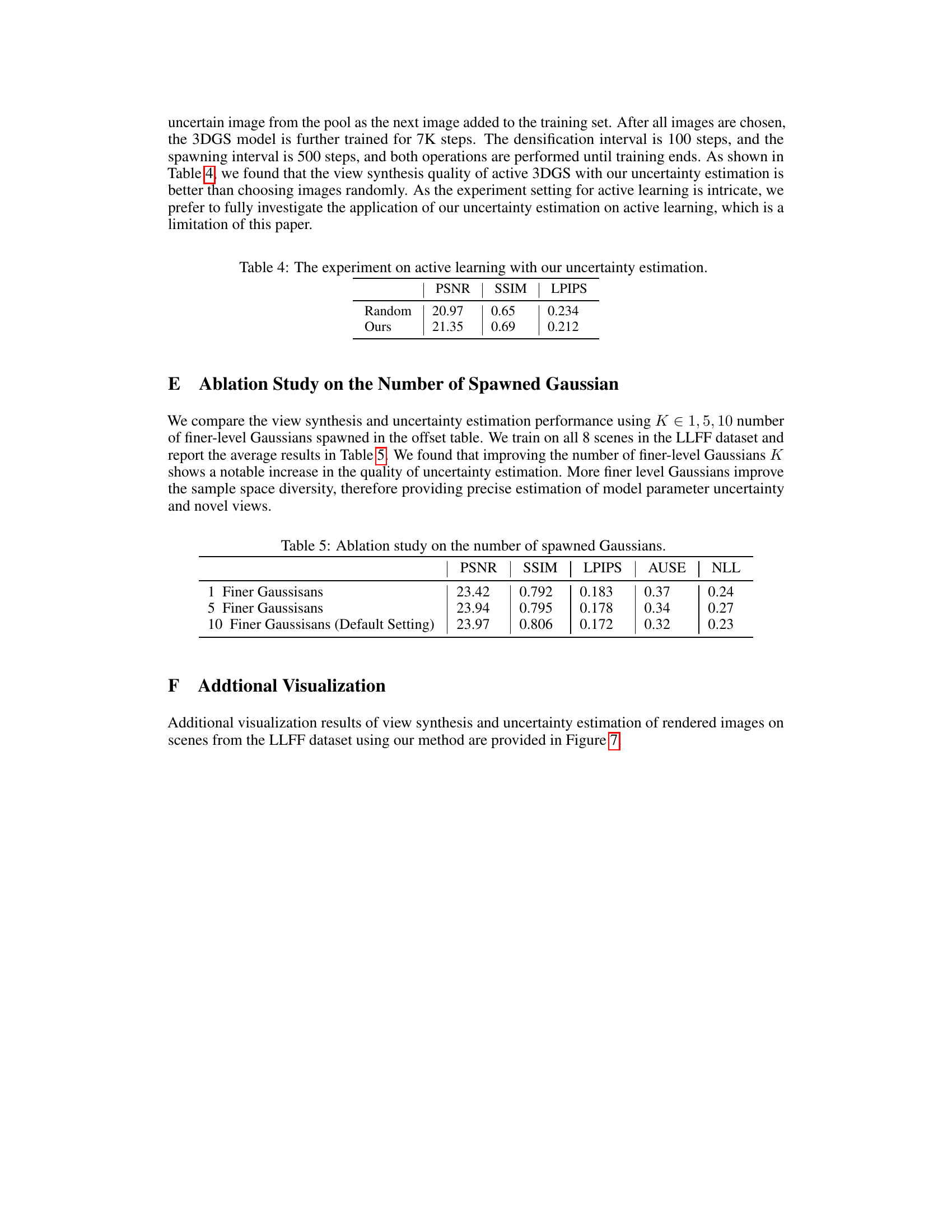
🔼 This table presents the inference time in seconds for different variants of the proposed multi-scale variational inference method and compares it against the ensemble method. The variants differ in the number of parameters being offset: -
Ours_{full}offsets all parameters (position, scale, color, opacity) -Ours_{p,S,c}offsets position, scale, and color -Ours_{p,S,α}offsets position, scale, and opacity. The results demonstrate the efficiency gains achieved by the proposed offset table technique in reducing the inference time compared to the ensemble method.read the caption
Table 3: Inference time for variants of our method and the ensemble method.
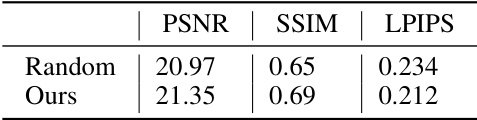
🔼 This table presents the results of an active learning experiment using the proposed uncertainty estimation method. It compares the performance of view synthesis (measured by PSNR, SSIM, and LPIPS) between randomly selecting training images and using the uncertainty map to guide the selection of the most informative images. The results show that using the proposed uncertainty-guided active learning approach improves the quality of view synthesis compared to random selection.
read the caption
Table 4: The experiment on active learning with our uncertainty estimation.

🔼 This table presents the results of an ablation study conducted to evaluate the impact of varying the number of spawned Gaussians (K) on the performance of the proposed multi-scale variational inference framework. The study varied K across three values (1, 5, and 10), assessing the impact on PSNR, SSIM, LPIPS, AUSE, and NLL. The results show that increasing the number of spawned Gaussians generally improves the quality of uncertainty estimation and view synthesis, highlighting the benefit of a diverse parameter sample space.
read the caption
Table 5: Ablation study on the number of spawned Gaussians.
Full paper#