↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current dynamic scene rendering methods based on Neural Radiance Fields (NeRF) are computationally expensive and struggle to achieve real-time performance. While 3D Gaussian Splatting (3DGS) offers improved speed, it suffers from noise in canonical 3D Gaussian coordinates and lacks effective 4D information aggregation. These issues limit rendering quality and hinder real-time applications.
The proposed DN-4DGS method tackles these challenges head-on. It introduces a Noise Suppression Strategy to refine the 3D Gaussian coordinates, removing noise before it impacts the rendering process. Further, it uses a Decoupled Temporal-Spatial Aggregation Module to effectively integrate temporal and spatial information, improving overall rendering quality. Extensive experiments show that DN-4DGS surpasses existing state-of-the-art methods in rendering quality while maintaining real-time performance.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in computer vision and graphics because it presents DN-4DGS, a novel method for real-time dynamic scene rendering that significantly improves rendering quality. Its novel noise suppression and decoupled temporal-spatial aggregation techniques address limitations of existing methods, opening avenues for further research in high-fidelity dynamic scene representation and real-time rendering applications. The provided code allows for easy reproduction and further development.
Visual Insights#

This figure shows a comparison of the proposed method’s performance against a baseline method (4DGaussian) on two different datasets: PlenopticVideo and HyperNeRF. The images display rendered scenes, and the numbers underneath each image indicate the Peak Signal-to-Noise Ratio (PSNR), a metric used to evaluate the quality of the reconstruction.
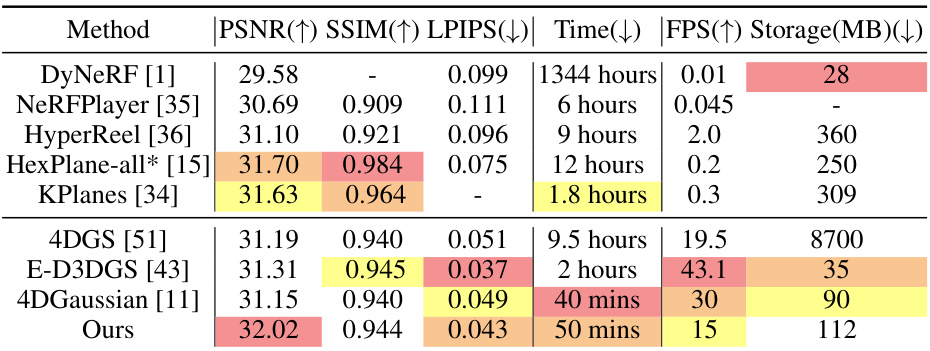
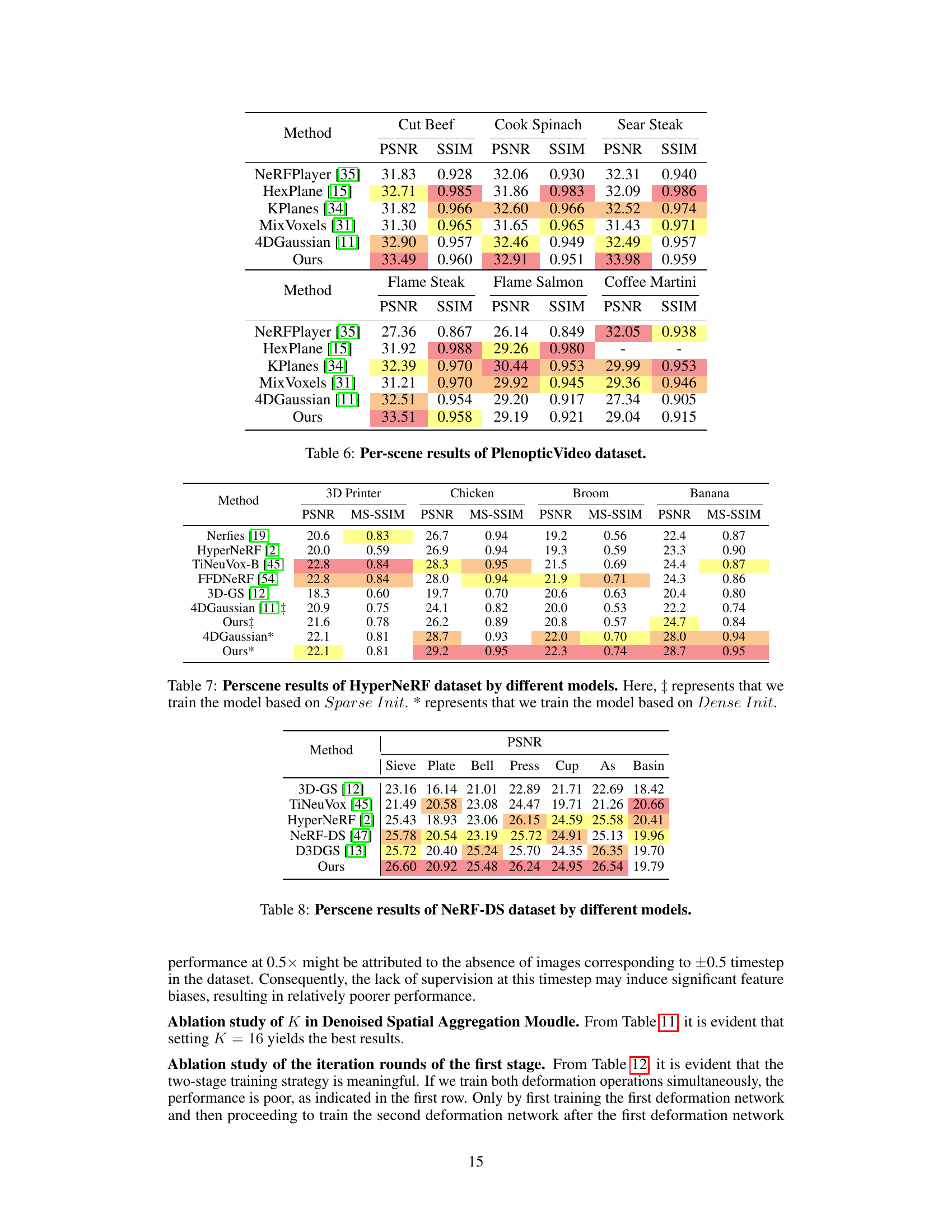
This table presents a quantitative comparison of different methods for novel view synthesis on dynamic scenes using the PlenopticVideo dataset. The metrics used are PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index), and LPIPS (Learned Perceptual Image Patch Similarity). Lower LPIPS values indicate better perceptual similarity to ground truth. The table compares various methods in terms of these metrics, rendering time, frames per second (FPS), and storage requirements. Color-coding highlights the top three performing methods for each metric.
In-depth insights#
Noise Suppression#
The concept of ‘Noise Suppression’ in the context of dynamic scene rendering using 3D Gaussian splatting is crucial for achieving high-fidelity results. The presence of noise in the canonical 3D Gaussian coordinates, synthesized from multi-frame images, directly impacts the accuracy of the deformation field. A key insight is that this noise propagates through the deformable network, affecting the final rendering quality. Therefore, effective noise suppression strategies are vital to ensure that the deformed 3D Gaussians accurately represent the dynamic scene. This might involve techniques that filter or regularize the canonical Gaussian coordinates before the deformation process, potentially using advanced filtering methods or machine learning approaches to learn denoising functions that are integrated into the overall network. The effectiveness of a noise suppression strategy directly relates to the accuracy and efficiency of the deformation field, which in turn influences the rendering quality. A well-designed noise suppression method could significantly improve the real-time capabilities of dynamic scene rendering systems.
4D Feature Agg#
The heading ‘4D Feature Agg’ suggests a method for aggregating features from four-dimensional data, likely spatiotemporal data in the context of a research paper on dynamic scene rendering. This would involve combining information from three spatial dimensions (x, y, z) and one temporal dimension (t). Effective 4D feature aggregation is crucial for capturing the motion and changes within dynamic scenes. A naive approach might simply concatenate the features from each dimension, but more sophisticated techniques would likely be used to capture correlations and relationships. Possible techniques include convolutional layers designed to handle 4D data, recurrent neural networks (RNNs), or graph convolutional networks (GCNs) if the data is represented as a graph. The success of the method depends heavily on how well it can capture intricate spatiotemporal relationships, potentially addressing challenges such as noise in the data or occlusions. The method’s implementation might use specialized layers for efficient 4D processing. The evaluation of ‘4D Feature Agg’ would focus on the improved quality of the rendered dynamic scenes, comparing it to simpler aggregation methods or other state-of-the-art approaches. Key metrics would likely be visual quality (PSNR, SSIM), rendering speed, and memory usage.
Real-time Rendering#
Real-time rendering, the capability to generate images instantly, is a crucial area in computer graphics. Traditionally, achieving real-time performance has necessitated compromises in visual fidelity. However, recent advancements in deep learning, particularly with neural radiance fields (NeRFs) and their variants, are revolutionizing this field. 3D Gaussian Splatting (3DGS), for example, presents a significant leap forward by rendering high-quality images at real-time speeds. Methods like Denoised Deformable Networks with Temporal-Spatial Aggregation (DN-4DGS) build on 3DGS, addressing limitations such as noise in canonical Gaussian representations and inadequate 4D information aggregation to produce even more impressive results. The key to success often lies in efficient data structures and algorithms, allowing for rapid rendering without sacrificing visual quality. While challenges remain, particularly concerning the handling of complex dynamic scenes and the computational costs associated with high-resolution rendering, the path toward ubiquitous real-time rendering of photorealistic scenes is rapidly progressing. Further research should focus on balancing computational efficiency with visual realism, exploring novel architectures and optimization techniques to make real-time rendering accessible for a wider range of applications.
Two-Stage Deformation#
The two-stage deformation approach is a core innovation for enhancing the accuracy and robustness of dynamic scene rendering. The first stage utilizes a standard deformation network on the canonical 3D Gaussians to suppress initial noise present in their coordinates, thereby refining their distribution. This initial denoising is crucial, as it prevents noise propagation through subsequent deformation networks. The second stage leverages this improved coordinate data for spatial aggregation, enhancing the precision of the deformation field, resulting in higher-quality rendering. This decoupled temporal-spatial approach ensures that the noise is effectively managed while still capturing the spatiotemporal dynamics, leading to more accurate and efficient deformation for dynamic scene rendering. The two-stage process is not only more robust to noisy input, but it also improves rendering quality under real-time constraints, making it a significant advancement in dynamic scene representation.
Future Work#
The authors acknowledge the limitations of their two-stage deformation approach, specifically mentioning the lack of simultaneous supervision for both stages, leading to unpredictable coordinate deformation in the second stage. Future work should prioritize simultaneous supervision to improve control and accuracy. They also suggest exploring the integration of spatial feature aggregation within the deformation operations. This implies investigating more sophisticated aggregation techniques that handle noisy inputs effectively. Furthermore, given that the current work focuses on real-time rendering, exploring techniques to further enhance speed and efficiency while maintaining high fidelity is a crucial area for future research. This could involve optimizing the network architecture, exploring different aggregation methods, or developing novel lightweight representations for dynamic scenes. The potential for extending the approach to handle more complex dynamic scenes with occlusion and greater variability in object motion is also a significant avenue for investigation. Finally, a thorough comparative analysis against other state-of-the-art methods on a wider range of datasets is needed to firmly establish the generality and robustness of the proposed method.
More visual insights#
More on figures

This figure compares the rendering results of the proposed method (DN-4DGS) with the baseline method (4DGaussian) on the HyperNeRF dataset. It visually demonstrates the two-stage deformation process in DN-4DGS, showing how the initial noisy canonical 3D Gaussians are progressively refined to produce higher-quality deformable Gaussians that better match the ground truth. The yellow box highlights the improvement achieved by the two-stage deformation process.
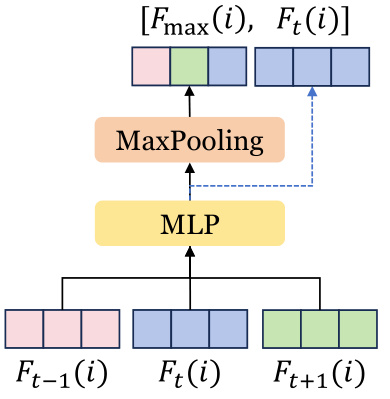
This figure illustrates the architecture of the Temporal Aggregation Module within the DN-4DGS model. It shows how temporal information is aggregated from adjacent frames (t-1, t, t+1). Feature encoding is first performed on the features at each timestep (Ft-1(i), Ft(i), Ft+1(i)). These features are then concatenated and passed through a Multi-Layer Perceptron (MLP) followed by a MaxPooling operation to generate the final aggregated feature Fmax(i). This is then combined with the original time t feature, Ft(i), and a learnable embedding, Yi, to create the final deformation output, Ft(i)’.

This figure shows a comparison of the canonical 3D Gaussians generated using two different initialization methods: Sparse Init and Dense Init. Sparse Init uses a point cloud provided by the HyperNeRF dataset, while Dense Init generates a denser point cloud. The results show that Dense Init produces higher-quality rendering, but at the cost of increased computational resources. The images illustrate the difference in the quality and density of the Gaussian distributions generated by the two methods.

This figure provides qualitative comparisons between the results of 4DGaussian and the proposed DN-4DGS method on the PlenopticVideo dataset. The images show different scenes from the dataset, and the comparison highlights the improved rendering quality achieved by DN-4DGS, particularly in terms of detail and sharpness, as indicated by the red boxes.

This figure presents a qualitative comparison of the results obtained using 4DGaussian and the proposed method (DN-4DGS) on the HyperNeRF dataset. The results are shown for both sparse and dense Gaussian initialization. Each row shows a sequence of images from a video, comparing the rendering results of the two methods against the ground truth. The numbers in gray cells indicate the PSNR (Peak Signal-to-Noise Ratio) values, a quantitative metric of image quality.

This figure compares the canonical results (i.e., the initial 3D Gaussian representation before deformation) generated by 4DGaussian and D3DGS methods. It visually demonstrates the difference in noise level between the two approaches before the deformation process is applied. The image shows a yellow excavator on a wooden surface, and the visual noise of the 3D Gaussian splatting (3DGS) is quite visible. The differences seen in the figure highlight the impact of noise in the canonical 3D Gaussian representations and motivates the authors’ proposed Noise Suppression Strategy (NSS) in their method.

This figure shows the effectiveness of the two-stage deformation process in the DN-4DGS model. The first stage is a standard deformation that takes the coordinates x, y, z of the canonical 3D Gaussians and time t as input, and outputs corresponding coordinate deformations Δx, Δy, Δz. The second deformation builds upon the first by adding Δx, Δy, Δz to the original x, y, z, creating a modified set of coordinates that is then input into a new feature extraction network. The results show a significant reduction in noise after the first deformation stage, leading to a more accurate deformation field and improved rendering quality. PSNR values are given in the gray cells to quantify the improvement.

This figure compares the rendering results of canonical 3D Gaussians using two different initialization methods: Sparse Init and Dense Init. Sparse Init uses a point cloud from the HyperNeRF dataset for initialization, while Dense Init generates a denser point cloud. The results show that Dense Init produces better rendering quality, but it requires more computational resources. The figure demonstrates the impact of the quality of initial canonical 3D Gaussians on the overall rendering results.

The figure shows a qualitative comparison of rendering results between the 4DGaussian method and the proposed DN-4DGS method on the PlenopticVideo dataset. The comparison highlights the improved rendering quality achieved by DN-4DGS, particularly in areas with complex motion and fine details. The results are presented for several scenes from the dataset, showcasing the superiority of DN-4DGS in handling dynamic scenes with higher fidelity.

This figure shows more visualization results on canonical 3D Gaussians generated by two methods: Sparse Init and Dense Init. Sparse Init uses the point cloud from HyperNeRF dataset, while Dense Init generates denser point cloud. Although Dense Init produces better quality, it is computationally more expensive.

This figure showcases a qualitative comparison of rendering results between the 4DGaussian method and the proposed DN-4DGS method on the PlenopticVideo dataset. Each row represents a different scene within the dataset, showing a sequence of frames. The left column displays the results generated by 4DGaussian, the middle column the results from DN-4DGS, and the right column the ground truth images. The comparison allows for a visual assessment of the relative rendering quality and artifact presence between the two methods.
More on tables
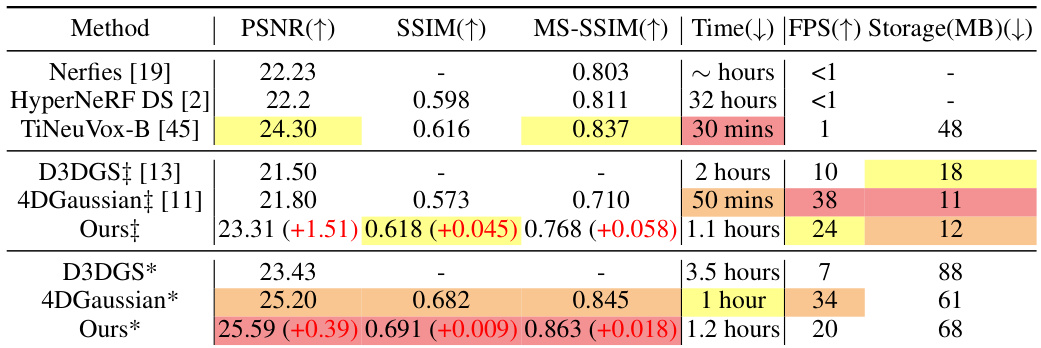
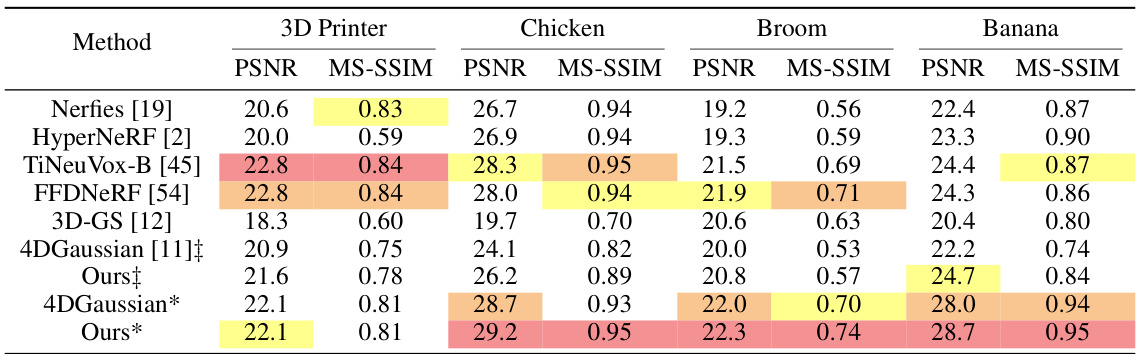
This table presents a quantitative comparison of different methods for novel view synthesis on the HyperNeRF dataset. It compares metrics like PSNR, SSIM, and MS-SSIM to evaluate the quality of the rendered images. The table also includes training time, frames per second (FPS), and storage requirements for each method. The results are shown separately for both ‘Sparse Init’ (using a sparse point cloud for Gaussian initialization) and ‘Dense Init’ (using a denser point cloud). This allows for comparison of the methods’ performance under different initialization conditions.
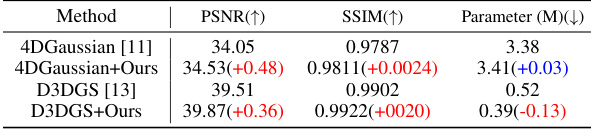
This table compares the performance of four different methods on the D-NeRF dataset. The methods are 4DGaussian, 4DGaussian with the proposed method (4DGaussian+Ours), D3DGS, and D3DGS with the proposed method (D3DGS+Ours). The metrics used for comparison are PSNR, SSIM, and the number of parameters (in millions) in the deformation networks. The improvements achieved by adding the proposed method to both 4DGaussian and D3DGS are highlighted. Notably, the proposed method leads to a reduction in parameters in D3DGS while still improving performance.
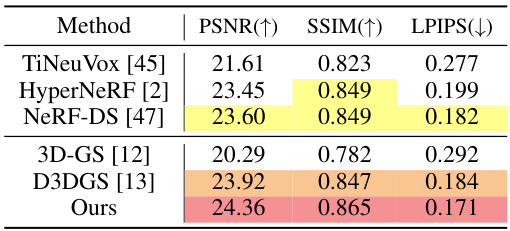
This table presents a quantitative comparison of different methods on the NeRF-DS dataset. The methods compared include TiNeuVox, HyperNeRF, NeRF-DS, 3D-GS, D3DGS, and the proposed method (Ours). The metrics used for comparison are PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index), and LPIPS (Learned Perceptual Image Patch Similarity). Higher PSNR and SSIM values indicate better image quality, while a lower LPIPS value indicates greater perceptual similarity to the ground truth. The table highlights the improved performance of the proposed method compared to the baseline methods.
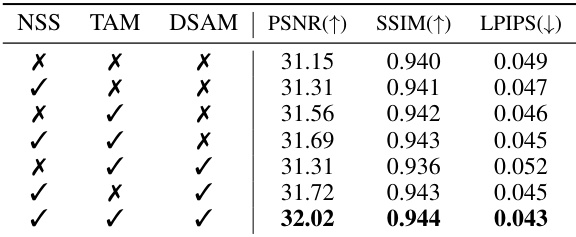
This table presents the ablation study results on the PlenopticVideo dataset to evaluate the effectiveness of different components in the DN-4DGS model. It shows the impact of using the Noise Suppression Strategy (NSS), Temporal Aggregation Module (TAM), and Denoised Spatial Aggregation Module (DSAM) individually and in combination on PSNR, SSIM, and LPIPS metrics. The results demonstrate the contributions of each module and their synergistic effects on improving the overall rendering quality.
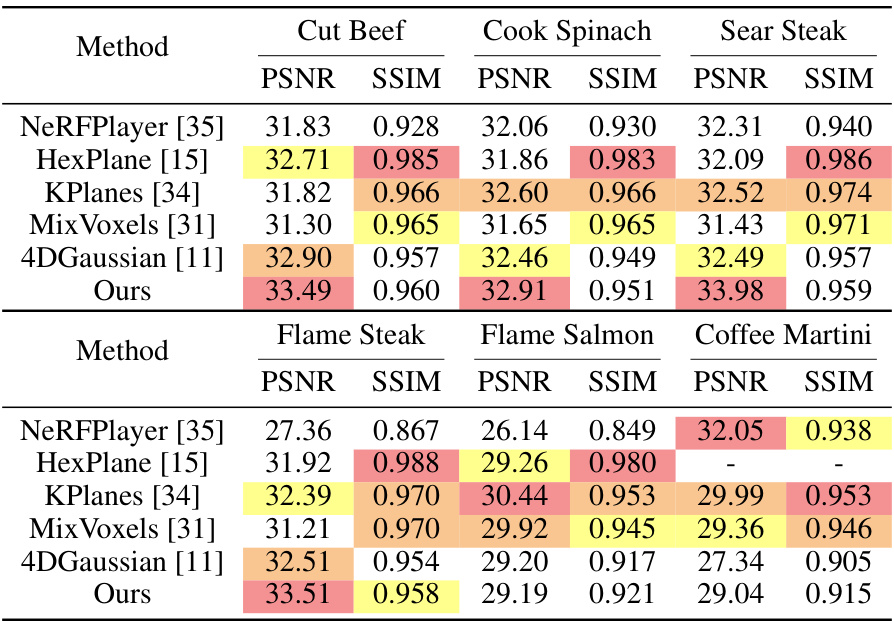
This table presents a quantitative comparison of different methods for novel view synthesis on dynamic scenes using the PlenopticVideo dataset. It compares the methods’ performance based on Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), and Learned Perceptual Image Patch Similarity (LPIPS) metrics. The best, second best, and third-best results for each metric are highlighted.
This table presents a quantitative comparison of different methods for novel view synthesis on dynamic scenes using the PlenopticVideo dataset. The comparison is based on three metrics: PSNR, SSIM, and LPIPS (Alex). Each metric’s value is color-coded to easily identify the top three performing methods for each scene. The table provides a summary of the performance across all scenes in the dataset.
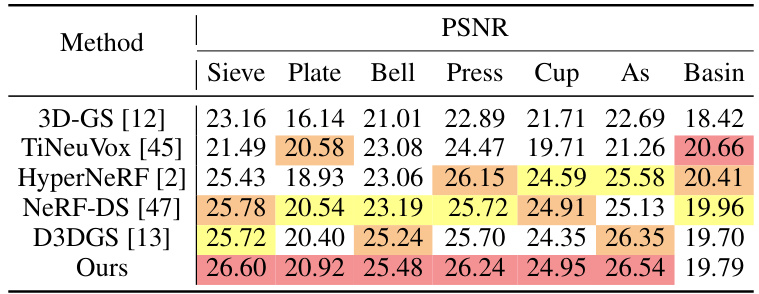
This table presents a quantitative comparison of different methods on the NeRF-DS dataset for novel view synthesis. The table shows the PSNR values achieved by each method on seven different scenes: Sieve, Plate, Bell, Press, Cup, As, and Basin. The ‡ and * symbols indicate whether the model was trained using sparse or dense initialization, respectively. The table allows for a detailed comparison of the performance of the proposed method against existing state-of-the-art techniques on a challenging dataset for dynamic scene rendering.
This table presents a quantitative comparison of different methods for novel view synthesis on dynamic scenes using the PlenopticVideo dataset. It compares the average Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), and Learned Perceptual Image Patch Similarity (LPIPS) scores achieved by each method. The best, second best, and third-best results for each metric are highlighted.
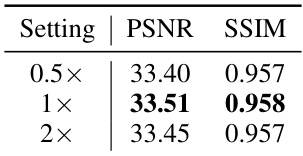
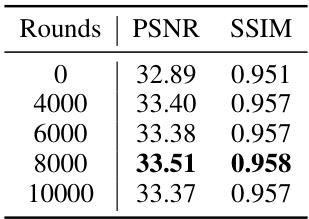
This ablation study investigates the impact of different time step values on the performance of the Temporal Aggregation Module within the DN-4DGS model. The results are specifically focused on the ‘flame steak’ scene from the PlenopticVideo dataset. The table shows that a timestep of 1x yields the best PSNR and SSIM scores, indicating optimal performance for this parameter.

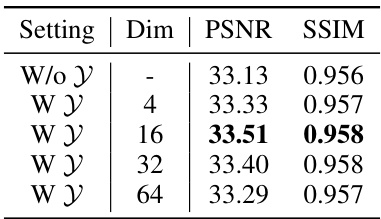
This ablation study analyzes the impact of changing the parameter K, which controls the number of nearest neighbors considered in the Denoised Spatial Aggregation Module (DSAM), on the model’s performance. The results demonstrate that K=16 yields the best performance, suggesting a balance between incorporating local context and computational efficiency.
This table presents a quantitative comparison of different methods for novel view synthesis on dynamic scenes using the PlenopticVideo dataset. It compares the methods based on their average PSNR, SSIM, and LPIPS (Alex) scores. The best, second-best, and third-best results for each metric are highlighted by color-coding the cells.
Full paper#