Cascade of phase transitions in the training of energy-based models

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with energy-based models and deep learning. It provides novel insights into the learning dynamics, reveals a series of previously unknown phase transitions, and offers practical guidance for improving training and understanding model behavior. The findings advance our understanding of high-dimensional probability distributions and could inspire new training methods and theoretical frameworks.

Visual Insights

#

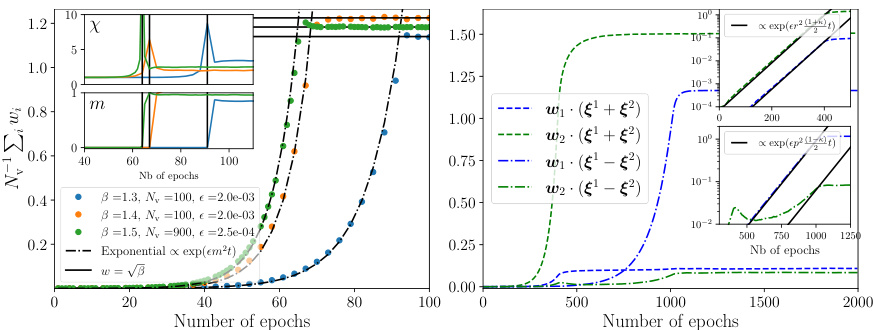
This figure shows the learning dynamics of a Binary-Gaussian Restricted Boltzmann Machine (BG-RBM) with one hidden node trained on data generated by the Mattis model. The left panel illustrates the model’s susceptibility and magnetization, revealing a phase transition. The right panel shows learning curves for RBMs learning two correlated patterns, demonstrating exponential growth in different phases. Insets provide detailed views of the susceptibility and magnetization near the transition and illustrate exponential weight growth.

This table lists the hyperparameters used for training the Restricted Boltzmann Machines (RBMs) in the main part of the paper. For each dataset (MNIST, CelebA, HGD), different image sizes were used, resulting in variations in the number of visible units (Nv), hidden units (Nh), learning rate (ε), and minibatch size (Nms). These hyperparameters were selected to ensure effective training and analysis of the models.

In-depth insights

#

Phase Transition Cascade

#

The concept of a ‘Phase Transition Cascade’ in the context of training energy-based models offers a compelling framework for understanding the learning process. It suggests that learning isn’t a smooth, continuous process, but rather a series of discrete transitions, each marked by a qualitative shift in the model’s representational capacity. Each phase transition likely corresponds to the model successfully acquiring a new set of features, effectively segmenting its probability distribution into increasingly distinct modes. This progressive refinement allows the model to learn increasingly complex and nuanced relationships in the data. Analytical tractability is significantly improved by focusing on simplified model architectures and data distributions, thereby uncovering the underlying mathematical mechanisms behind these transitions. However, the generalizability of these findings to larger, more complex models and real-world datasets requires further investigation, which is often accomplished via numerical analysis on increasingly high-dimensional datasets. Numerical experiments are crucial to validate theoretical predictions and establish the robustness of the observed phase transitions. The key is to understand how the cascade unfolds, what factors influence the timing and characteristics of each transition, and what the ultimate implications are for model performance and the interpretation of learned representations.

RBM Learning Dynamics

#

The study of RBM learning dynamics reveals a fascinating interplay between data structure and model evolution. Phase transitions, marked by sharp changes in the singular values of the weight matrix, indicate the acquisition of new features. The model doesn’t simply learn all features at once; rather, it progresses through a cascade, first capturing coarse features (like the center of mass of data modes) and then progressively resolving finer details. This hierarchical learning process closely resembles the dynamics of physical systems undergoing phase transitions, offering a powerful lens for theoretical analysis. The research highlights the importance of the data’s intrinsic dimensionality and correlations, demonstrating how the model learns by sequentially aligning its parameters to the principal components of the data distribution. High-dimensional settings reveal that these phase transitions are not merely smooth crossovers, but actual critical phenomena with potentially valuable implications for training efficiency and model interpretability. The theoretical analysis, confirmed by experiments on real-world datasets, provides valuable insights into the underlying mechanisms driving the learning process and offers a framework to further explore the complex interplay of data, model architecture, and learning dynamics in energy-based models.

High-Dimensional Learning

#

High-dimensional learning presents unique challenges due to the curse of dimensionality, where data sparsity and computational complexity increase exponentially with the number of features. Effective dimensionality reduction techniques are crucial, often employing methods like principal component analysis (PCA) to capture the most significant variance. Understanding the dynamics of learning in high-dimensional spaces is critical; models may exhibit different behaviors, including phase transitions, not observed in lower dimensions. Robustness and generalization are major concerns. High-dimensional models are prone to overfitting; regularization techniques become essential. Theoretical analysis frequently leverages tools from statistical mechanics and random matrix theory, offering insights into the behavior of complex systems. Successfully navigating the challenges of high-dimensional learning requires a multi-faceted approach combining advanced algorithms, careful analysis, and a solid understanding of statistical properties.

Feature Encoding Process

#

The feature encoding process in energy-based models, particularly Restricted Boltzmann Machines (RBMs), is a complex interplay of data characteristics and model dynamics. The paper reveals a cascade of phase transitions during training, each associated with the acquisition of new features and marked by a divergence in the system’s susceptibility. Initially, the RBM learns the overall distribution’s center of mass. Subsequently, progressive learning of principal modes occurs through a series of second-order phase transitions, representing a hierarchical clustering of data. This process involves a gradual refinement of features from coarse-grained representations to a fine-grained understanding, effectively segmenting the learned probability distribution. High-dimensional data exhibits sharper transitions, emphasizing the relevance of the theoretical findings in practical applications. The analytical framework, utilizing simplified model architectures, provides valuable insights into the fundamental mechanisms underlying feature learning. These theoretical predictions are successfully validated through numerical experiments on real-world datasets, supporting the observation of phase transitions and the link between feature encoding and model dynamics.

Finite-Size Scaling

#

Finite-size scaling (FSS) is a crucial concept in statistical physics and its application to machine learning, especially when dealing with phase transitions in high-dimensional systems. It addresses the challenge of observing sharp phase transitions in finite-size systems, which often appear as smooth crossovers. The core idea is that the behavior of a finite system near a critical point can be related to the behavior of an infinite system through scaling functions that incorporate the system size as a relevant parameter. In the context of the research paper, FSS is used to analyze how phase transitions in Restricted Boltzmann Machines (RBMs) evolve as the number of visible and hidden units changes. By applying FSS analysis, the researchers provide strong evidence that the observed transitions are indeed true phase transitions, and not simply finite-size effects. The mean-field FSS ansatz is particularly important for validating that the universality class of these transitions aligns with theoretical predictions. This rigorously confirms the existence of second-order phase transitions during RBM training, providing further insight into the learning dynamics of the model. The results support the validity of theoretical models in high dimensions and demonstrate the power of FSS analysis in revealing fundamental properties of high-dimensional systems.

More visual insights

#

More on figures

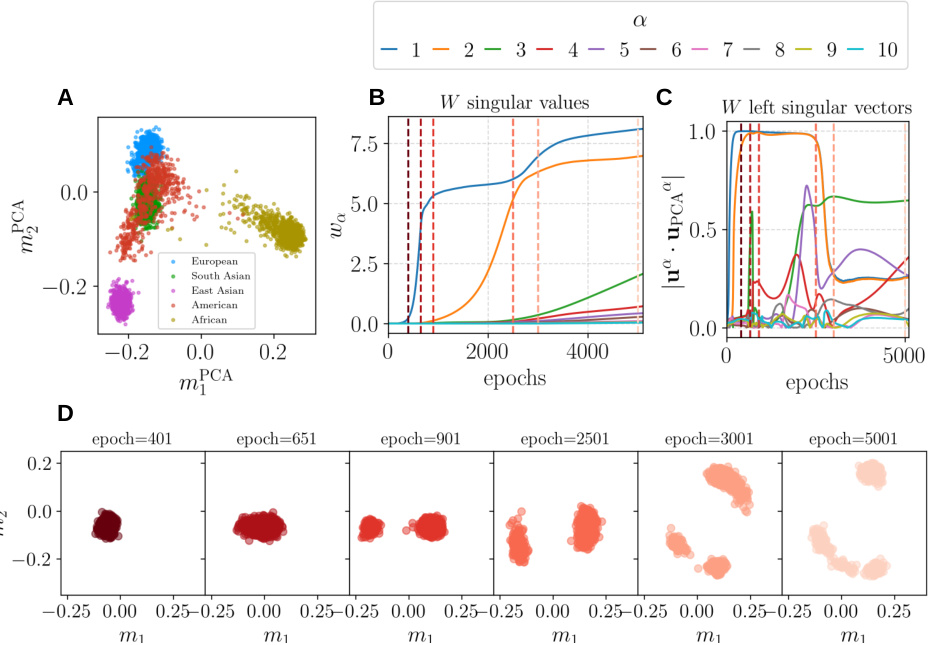
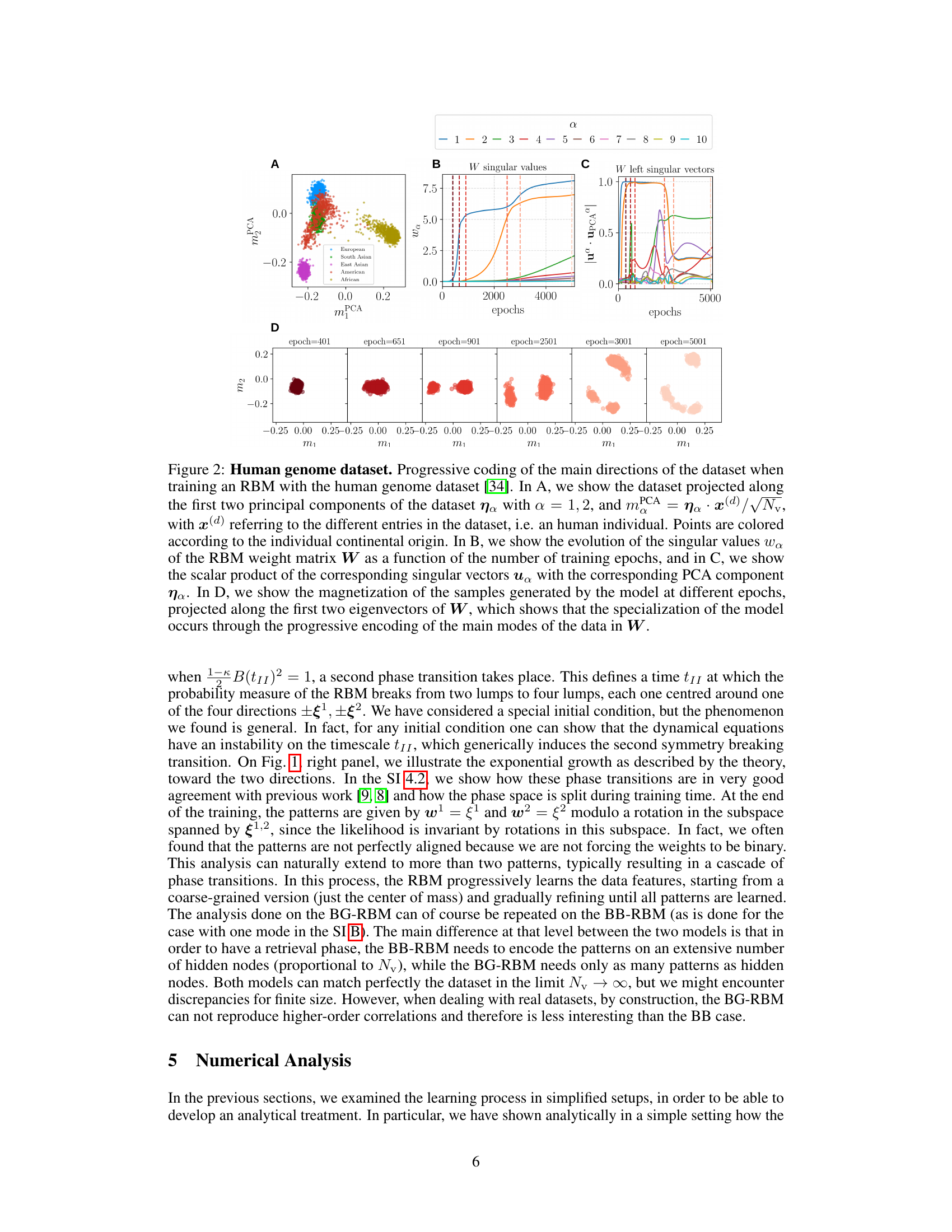
Figure 2 shows the progressive learning of the main directions of a human genome dataset using a Restricted Boltzmann Machine (RBM). Panel A displays the dataset projected onto its first two principal components, colored by continental origin. Panel B illustrates the evolution of the RBM’s singular values during training, reflecting the progressive learning of the dataset’s structure. Panel C depicts the alignment of the RBM’s singular vectors with the dataset’s principal components. Finally, panel D visualizes the model’s learned distribution at different training stages, highlighting the progressive encoding of the main modes through a series of phase transitions.

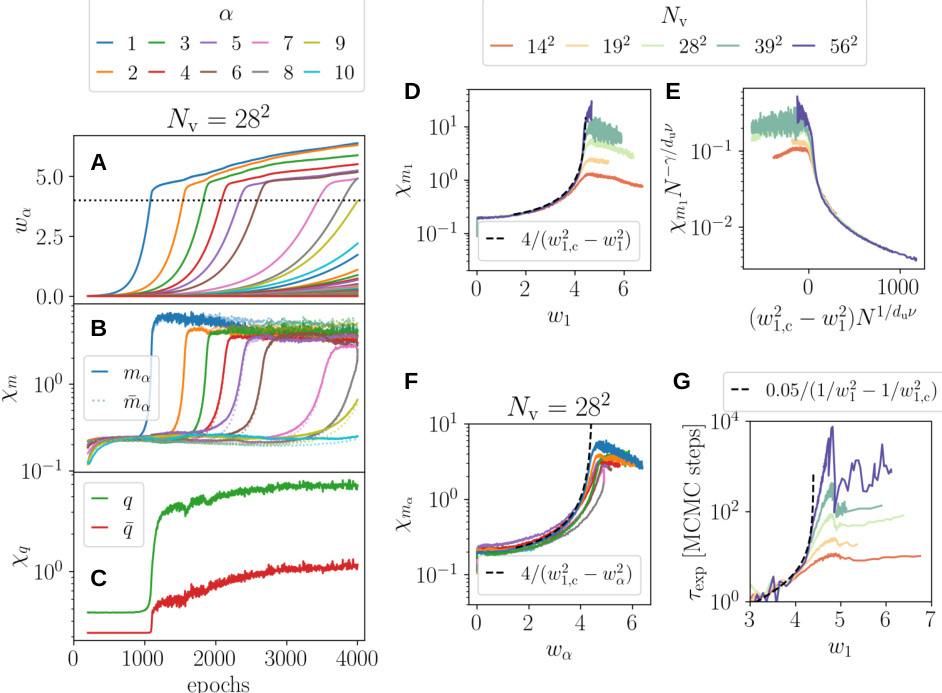
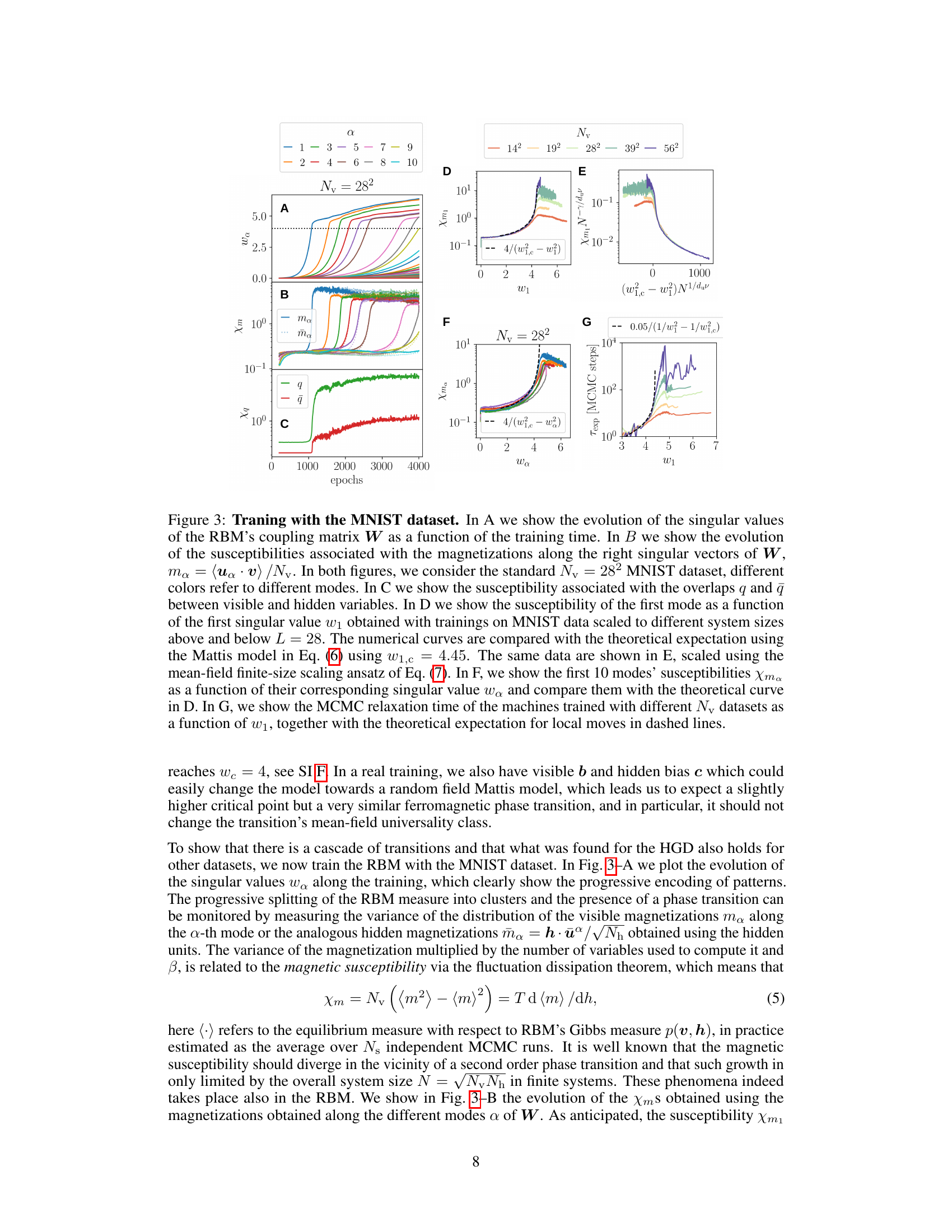
This figure shows the results of training Restricted Boltzmann Machines (RBMs) on the MNIST dataset with different system sizes. Panel A displays the evolution of singular values of the weight matrix over training epochs. Panel B shows the susceptibilities associated with magnetizations along right singular vectors. Panel C shows susceptibilities related to overlaps between visible and hidden units. Panel D compares the susceptibility of the first mode (obtained with various system sizes) to a theoretical model prediction. Panel E shows the same data after finite-size scaling. Panel F shows susceptibilities for the first 10 modes, and panel G shows MCMC relaxation time.

Figure 4 presents the numerical analysis performed on two datasets, CelebA and HGD. Panel A shows the hidden susceptibility for different system sizes in the CelebA dataset. Panel B shows the mean-field finite-size scaling (FFS) associated with the first transition. Panels C and D show the visible susceptibility for the first phase transition in the HGD dataset. Panel E shows the hysteresis in the low-temperature phase for CELEBA (128x128).

This figure shows the learning behavior of a Binary-Binary Restricted Boltzmann Machine (RBM) trained on data generated by the Mattis model. The left panel displays the exponential growth of the weights (singular values) as a function of training epochs for different system sizes and learning rates. The right panel illustrates the dynamics of the RBM, showing the alignment of the eigenvector with the pattern ξ and the subsequent exponential growth of the eigenvalue until a phase transition occurs.

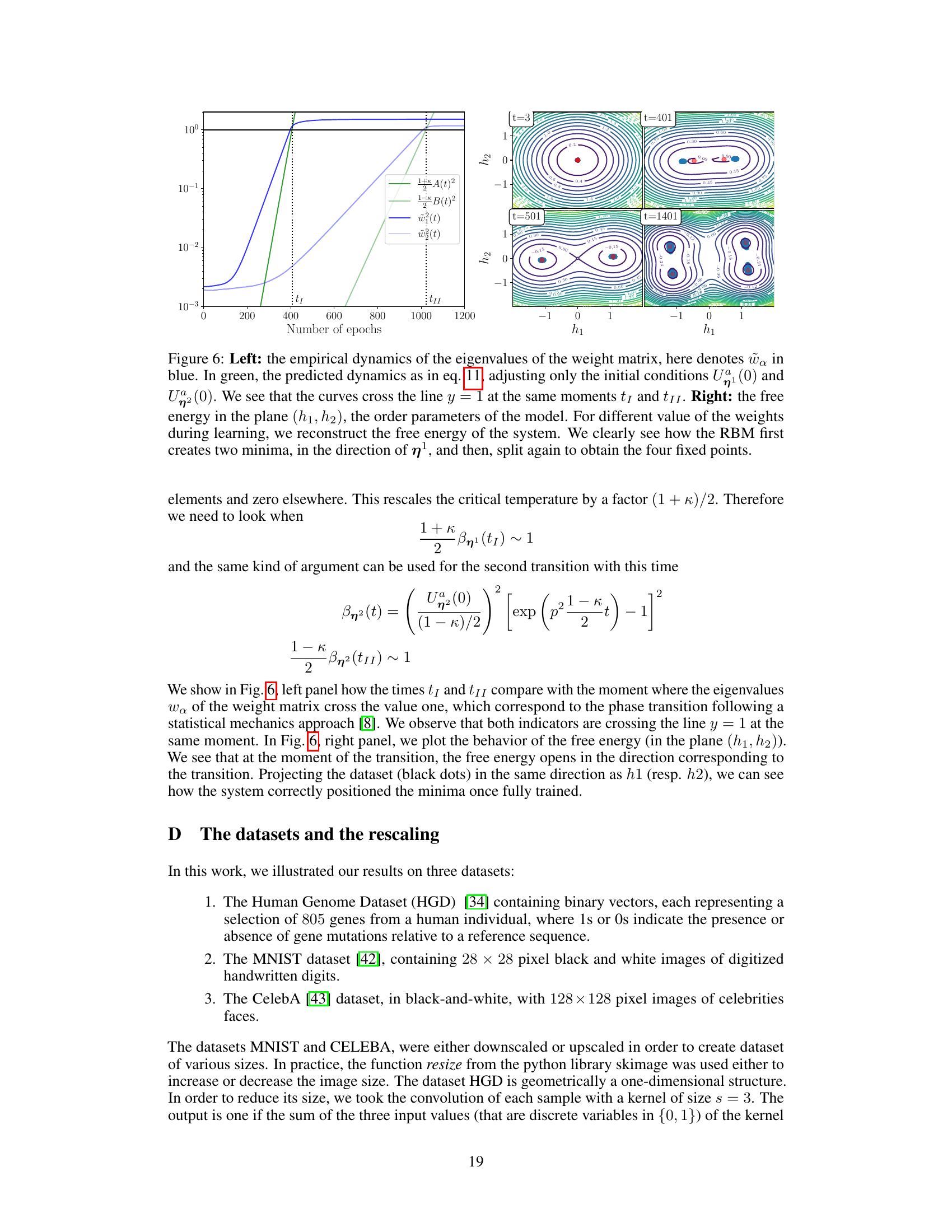
The left panel shows the evolution of eigenvalues of the weight matrix during learning. The blue line represents empirical data, while the green line represents the model prediction. Both lines cross y=1 at the same times (t1 and t11), indicating phase transitions. The right panel visualizes the free energy landscape of the model at different learning stages. It shows how the RBM first develops two minima (along the direction n¹) and subsequently splits into four minima.

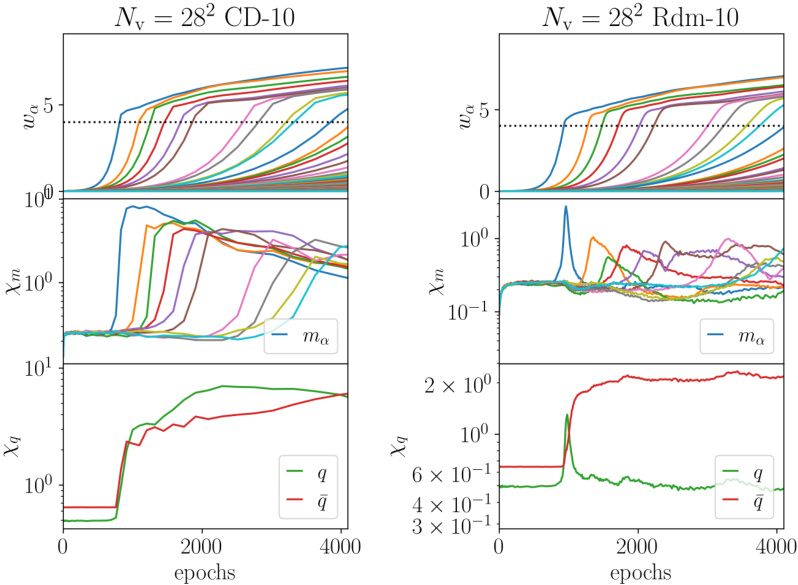
This figure shows the results of training a Restricted Boltzmann Machine (RBM) on the MNIST dataset. It demonstrates the progressive learning of data features through a series of phase transitions, visualized through singular value decomposition (SVD) of the weight matrix, susceptibilities, and relaxation times. The figure provides both empirical results and theoretical comparisons using a Mattis model.

Full paper

#