TL;DR#
Many current methods for solving inverse problems using diffusion or flow models require a large number of steps, which is computationally expensive. This research tackles this issue by focusing on improving sampling efficiency. Existing methods often involve complex and computationally intensive steps to achieve high-quality results in image processing tasks like super-resolution.
The proposed method introduces Conditional Conjugate Integrators (CCI). CCI projects the conditional diffusion/flow dynamics into a more efficient space for sampling, significantly reducing the number of steps needed. The researchers demonstrate its effectiveness across various linear image restoration tasks (super-resolution, inpainting, deblurring) and datasets, achieving state-of-the-art results with fewer steps than competitive baselines. This method is compatible with multiple iterative refinement models.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in image processing and generative modeling. It offers a significant speedup in solving inverse problems like super-resolution and inpainting, surpassing existing methods. Its framework is generalizable to various models and inverse problems, opening new avenues for research in efficient sampling techniques and high-quality image generation.
Visual Insights#

🔼 This figure illustrates the Conditional Conjugate Integrators method for fast sampling in inverse problems. It shows how the method projects the complex diffusion/flow dynamics into a simpler space for easier sampling, then projects the result back to the original space. This improves sampling speed and quality.
read the caption
Figure 1: Illustration of Conditional Conjugate Integrators for Fast Sampling in Inverse Problems. Given an initial sampling latent xt, at time ts, our sampler projects the diffusion/flow dynamics to a more amenable space for sampling using a projector operator Φ which is conditioned on the degradation operator H and the sampling guidance scale w. The diffusion/flow sampling is then performed in the projected space. Post completion, the generated sample in the projected space is transformed back into the original space using the inverse of the projection operator, yielding the final generated sample. We define the form of the operator Φ in Section 2.2. Conditional Conjugate Integrators can significantly speed up sampling in challenging inverse problems and can generate high-quality samples in as few as 5 NFEs as compared to existing baselines, which require from 20-1000 NFEs (see Section 3).

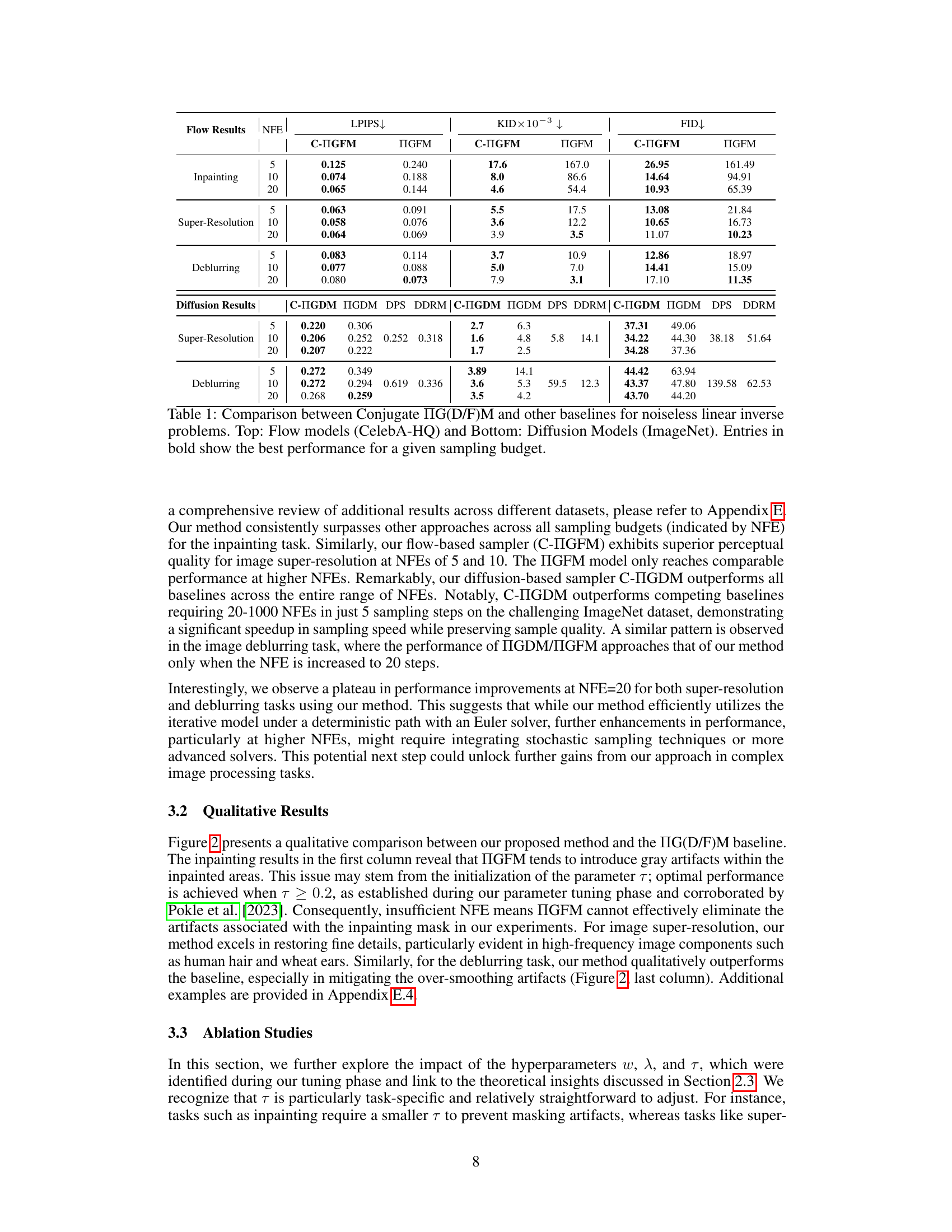
🔼 This table presents a quantitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against several baseline methods for solving three linear inverse problems: image super-resolution, inpainting, and Gaussian deblurring. The comparison is made across different sampling budgets (Number of Function Evaluations, NFE), using both diffusion and flow models. Metrics used for evaluation include LPIPS, KID, and FID to assess the perceptual quality of the generated images. The results demonstrate that the proposed method achieves superior performance, particularly at lower NFEs, suggesting it is more efficient and effective.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.
In-depth insights#
Inverse Problem Sampling#
Inverse problem sampling tackles the challenge of efficiently generating samples from a complex, often high-dimensional, posterior distribution. This is particularly relevant in scenarios where direct sampling is computationally infeasible due to the complexity of the forward model. The core idea is to leverage pre-trained generative models, such as diffusion models or normalizing flows, which excel at generating samples from simpler prior distributions. By cleverly incorporating information about the inverse problem, we can guide the sampling process towards the desired posterior. Efficient techniques are crucial because inverse problems often demand numerous iterations to achieve satisfactory results. Methods like Conditional Conjugate Integrators intelligently project the problem’s dynamics to a more manageable space, leading to significant speedups. This plug-and-play framework avoids retraining large models for specific inverse problems, thus enhancing the efficiency and flexibility of the sampling process. The efficacy of the approach is demonstrated across various inverse problems like super-resolution and inpainting, showcasing its potential to accelerate solutions for many applications.
Conditional Integrators#
The concept of “Conditional Conjugate Integrators” presented in the paper offers a novel approach to accelerate sampling in inverse problems within the framework of iterative refinement models. It leverages the structure of the inverse problem by projecting the conditional diffusion or flow dynamics into a more amenable space. This projection, achieved via a carefully designed operator conditioned on the degradation operator and sampling guidance scale, significantly improves sampling efficiency. The key innovation lies in decoupling the linear and non-linear components of the dynamics and employing an analytical solution for linear coefficients, leading to a faster convergence rate. This method is particularly effective for linear inverse problems and significantly outperforms baselines on tasks like super-resolution and inpainting, achieving high-quality results with considerably fewer sampling steps. However, its applicability to non-linear inverse problems remains a key area for future exploration, along with investigating alternative choices for the projection operator to further enhance performance and expand the method’s practical use. The theoretical analysis provides crucial insights into the design choices and properties of the proposed method. Its plug-and-play nature, relying solely on pre-trained models, makes it a promising technique for various inverse problems.
Linear Inverse Problems#
Linear inverse problems, where the relationship between observed data and underlying signal is linear, are a core focus in many scientific fields. Efficiently solving these problems often involves balancing speed and accuracy. The paper explores methods to dramatically speed up the sampling process for generating high-quality solutions using diffusion models and flow-matching models. A key contribution is the introduction of Conditional Conjugate Integrators, which intelligently project the problem into a more amenable space for sampling, leveraging the specific structure of the inverse problem itself. This approach proves particularly effective for challenging tasks such as super-resolution, demonstrating significant improvements in speed over existing baselines. The analysis highlights the importance of careful parameter tuning to optimize performance and the theoretical underpinnings are presented to provide a solid foundation for the proposed framework. Further extensions to noisy and non-linear inverse problems are also discussed, showing the flexibility and potential of the methodology for broad applications.
Noisy Problem Extensions#
The extension to noisy problems is a crucial aspect of the research, as real-world applications rarely involve perfectly clean data. The authors acknowledge this limitation and propose an approach to address it. Their strategy likely involves modifying the core algorithm to incorporate a noise model, potentially by adding a noise term to the observed data or by adjusting the optimization process to account for uncertainty. The success of this extension hinges on whether the modified algorithm can still achieve high-quality results while maintaining computational efficiency. A key question is how the proposed method handles varying noise levels and different types of noise. A thorough evaluation on datasets with varying levels of noise is necessary to assess the robustness and performance of the proposed method in noisy conditions. The effectiveness in noisy scenarios will largely determine the practical applicability of the work. It’s vital to explore how the theoretical properties of the method hold up with noise, and whether any adjustments to hyperparameters or the overall algorithm are needed for optimal results.
Future Research#
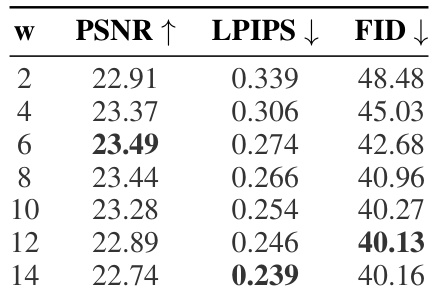
Future research directions stemming from this work could explore several promising avenues. Extending the framework to handle blind inverse problems, where the degradation operator is unknown, would significantly broaden the applicability. Investigating alternative numerical solvers beyond the Euler method, such as higher-order schemes or stochastic methods, could potentially improve sampling efficiency and quality at higher sampling budgets. Exploring the impact of different score function parameterizations and analyzing their effect on the sampler’s performance offers another promising direction. Finally, adapting the methodology to latent diffusion models and investigating its benefits for more complex tasks such as video generation or 3D reconstruction would be valuable future work. The robustness and generalizability of the proposed framework across different model architectures and various modalities remains a rich area for further investigation.
More visual insights#
More on figures

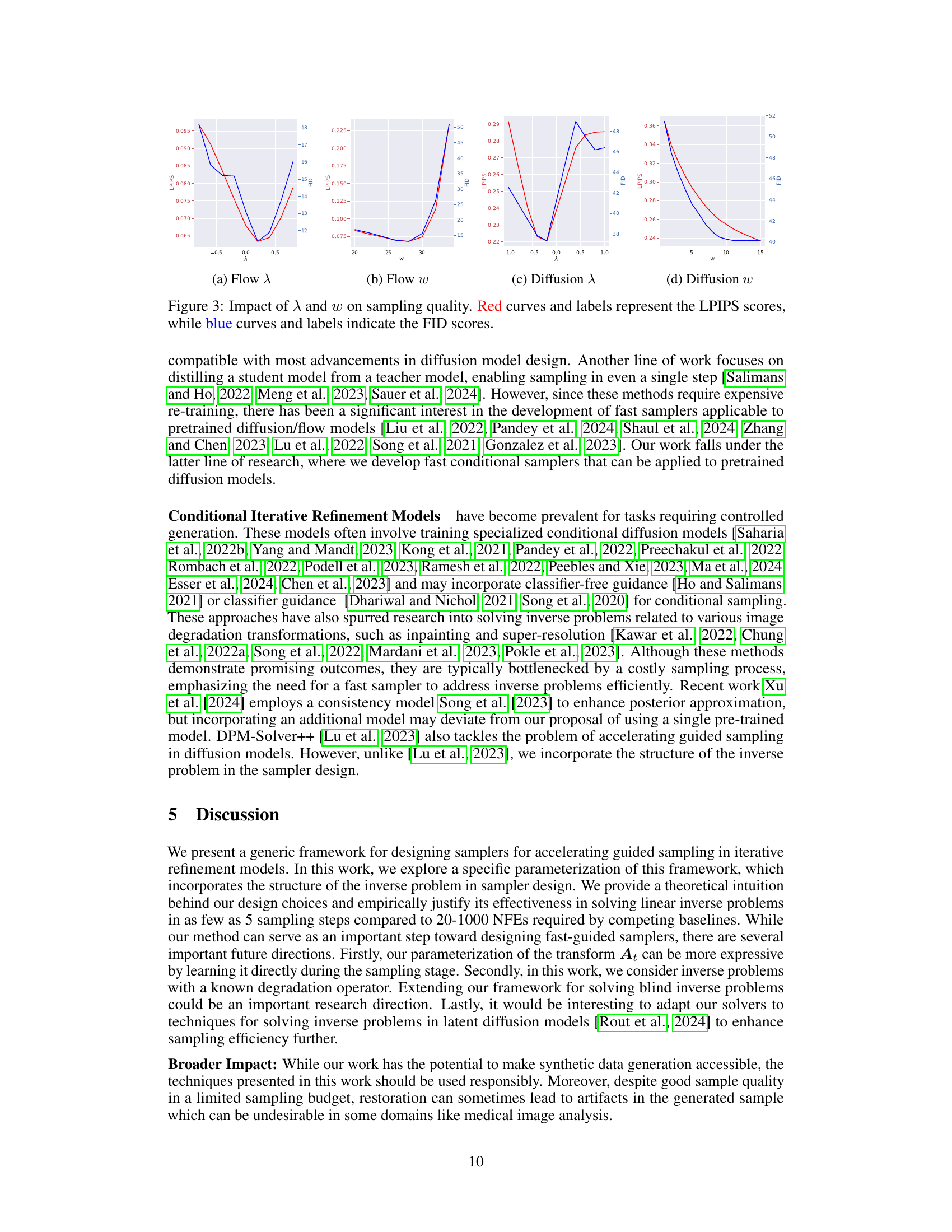
🔼 This figure compares the image generation quality of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against the baseline methods IG(D/F)M for five different datasets and tasks. The tasks are inpainting, deblurring, and 4x super-resolution. The results show that C-IG(D/F)M produces better quality images, especially regarding high-frequency details, with only 5 sampling steps. The improved performance highlights the efficiency of C-IG(D/F)M in solving inverse problems.
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure showcases a qualitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against the baseline IG(D/F)M across five different datasets and three different image restoration tasks (inpainting, deblurring, and super-resolution). The results demonstrate the superior visual quality of C-IG(D/F)M, especially in preserving high-frequency details, even when using a significantly smaller number of function evaluations (NFE=5).
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure presents a qualitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against the standard IG(D/F)M methods across five different datasets and three inverse problems: inpainting, deblurring, and super-resolution. The results show that C-IG(D/F)M produces higher-quality samples, particularly in preserving fine details, even with a significantly lower number of function evaluations (NFEs = 5). The use of C-IGFM is shown for inpainting, deblurring, and super-resolution on AFHQ, LSUN, and CelebA-HQ datasets, respectively. C-IGDM results are shown for super-resolution and deblurring on ImageNet and FFHQ datasets, respectively.
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure displays a qualitative comparison of image generation results between the proposed Conditional Conjugate Integrators (C-IG(D/F)M) and the baseline IG(D/F)M methods. It showcases the improvements achieved by C-IG(D/F)M across five datasets (AFHQ, LSUN, CelebA-HQ, ImageNet, and FFHQ) and five tasks (inpainting, deblurring, and 4x super-resolution). The comparison highlights the superior quality of images generated by C-IG(D/F)M, particularly with respect to detail preservation and artifact reduction, achieved with a low sampling budget (NFE=5).
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure shows a qualitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) method against the baseline IG(D/F)M method for five different datasets and three different tasks: inpainting, de-blurring, and 4x super-resolution. The results demonstrate the superior image quality produced by the C-IG(D/F)M method, even with a very low number of function evaluations (NFE=5). The figure highlights the improved visual detail and reduction of artifacts achieved using the proposed method compared to the baseline.
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure presents a qualitative comparison of the results obtained using the proposed Conditional Conjugate Integrators (C-IG(D/F)M) and the baseline IG(D/F)M methods across five different datasets and three inverse problems: inpainting, deblurring, and 4x super-resolution. The top row shows the original images followed by the results of applying pseudo-inverse methods for comparison. The following columns show results from the IG(D/F)M and the proposed C-IG(D/F)M methods using only 5 steps (NFE=5). The figure visually demonstrates the improved sample quality and efficiency of the proposed C-IG(D/F)M samplers compared to the baseline approach.
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure presents a qualitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against the standard IG(D/F)M methods. It showcases the results of both methods on five different datasets for five different tasks - inpainting, deblurring, and 4x super-resolution using both diffusion (C-IGDM) and flow-matching models (C-IGFM). The comparison highlights the superior image quality generated by C-IG(D/F)M despite utilizing only 5 steps, compared to the baselines that often require substantially more steps.
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure presents a qualitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against the baseline IG(D/F)M across various inverse problems, including inpainting, deblurring, and super-resolution. Results are shown for five different datasets: AFHQ, LSUN, CelebA-HQ, ImageNet, and FFHQ. The comparison highlights the improved sample quality achieved by C-IG(D/F)M, especially when using a small number of function evaluations (NFE=5).
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure displays a qualitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) method against the standard IG(D/F)M method for five different datasets. It showcases the results of three inverse problems: inpainting, deblurring, and 4x super-resolution. The top row shows the original, distorted, and results obtained by the IG(D/F)M and C-IG(D/F)M methods for three different datasets. The bottom row shows the results for the remaining datasets and inverse problems.
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure displays a qualitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) method against the baseline IG(D/F)M method for various image restoration tasks. Five datasets are used, showcasing results for inpainting, deblurring, and 4x super-resolution. The results demonstrate C-IG(D/F)M’s superior performance in generating higher-quality images, especially noticeable in the detail preservation and artifact reduction. The comparison uses a low number of function evaluations (NFE=5) to highlight the efficiency of the proposed method.
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)

🔼 This figure presents a qualitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against the baseline IG(D/F)M methods across five different datasets and three different tasks: inpainting, deblurring, and 4x super-resolution. The results show that C-IG(D/F)M produces visually superior results, especially in terms of fine details, even with only 5 NFE (number of function evaluations). The datasets used are AFHQ, LSUN, CelebA-HQ, ImageNet, and FFHQ.
read the caption
Figure 2: Qualitative comparison between C-IG(D/F)M and IG(D/F)M baselines on five different datasets. (a, b, c) Inpainting, De-blurring, and 4x Super-resolution with C-IGFM, respectively. (d,e) 4x Image Super-resolution and De-blurring with C-IGDM, respectively. (σy = 0, NFE=5)
More on tables
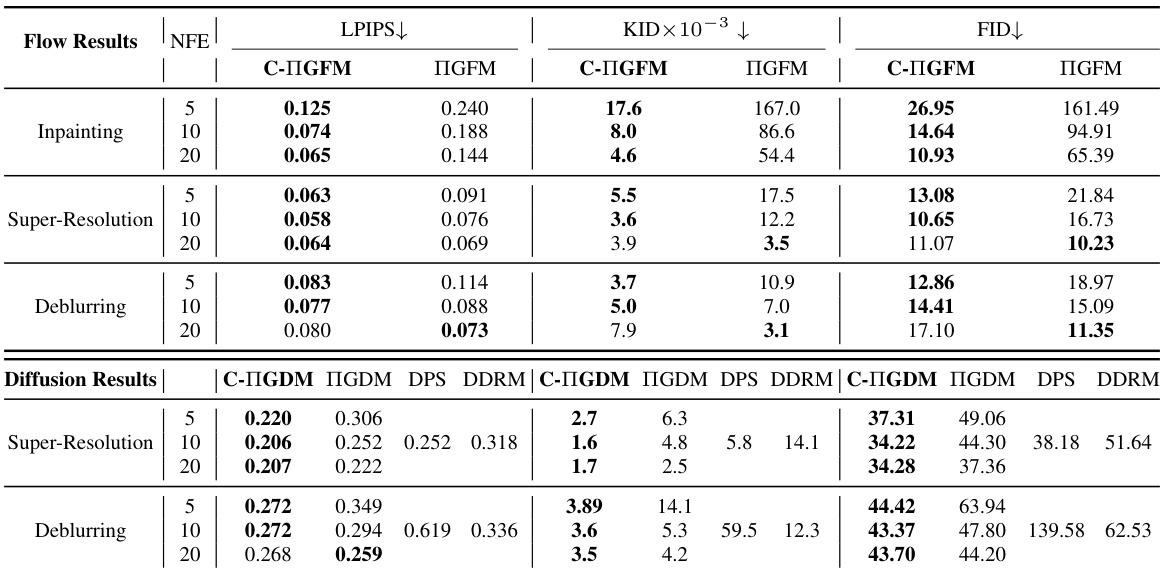
🔼 This table presents a comparison of the proposed Conditional Conjugate Integrators (C-IGDM and C-IGFM) against several baseline methods for solving three different noiseless linear inverse problems: image inpainting, super-resolution, and deblurring. Two different model types are used: diffusion models (evaluated on the ImageNet dataset) and flow models (evaluated on the CelebA-HQ dataset). The results are shown for different sampling budgets (NFEs), demonstrating the efficiency of the proposed methods. The best performance for a given NFE is highlighted in bold.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.

🔼 This table presents a quantitative comparison of the proposed Conditional Conjugate Integrators (C-IGDM and C-IGFM) against existing baselines (IGDM, IGFM, DPS, and DDRM) for three linear inverse problems: image super-resolution, inpainting, and deblurring. The results are shown for different sampling budgets (Number of Function Evaluations or NFEs), highlighting the efficiency and quality trade-off of the proposed method. The top half of the table shows results using flow models trained on the CelebA-HQ dataset, while the bottom half shows results using diffusion models trained on the ImageNet dataset.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.
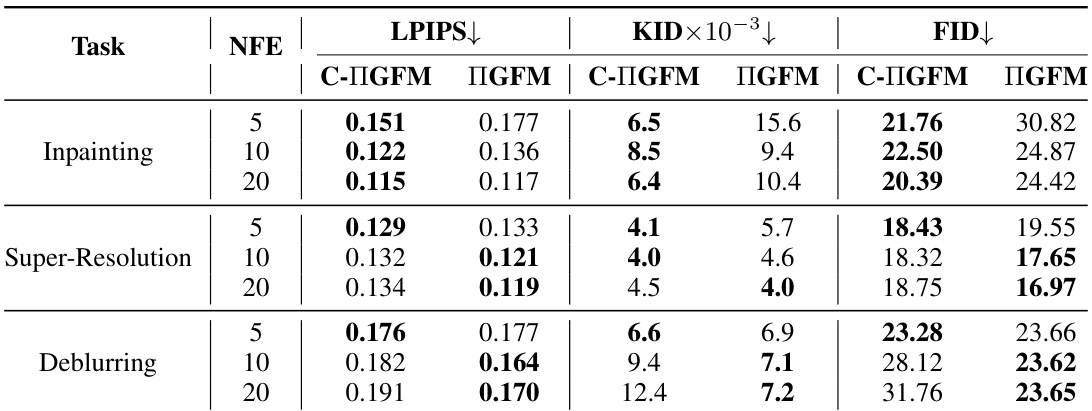
🔼 This table compares the performance of the proposed Conjugate IG(D/F)M samplers against other baselines on three linear inverse problems (super-resolution, inpainting, deblurring) using both flow and diffusion models. The results are presented for different numbers of function evaluations (NFEs), representing the sampling efficiency. Lower scores for LPIPS, KID, and FID indicate better sample quality. The table is split into two sections, one for flow models using the CelebA-HQ dataset and one for diffusion models using the ImageNet dataset.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.

🔼 This table presents a comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) with several baseline methods for solving three different noiseless linear inverse problems: inpainting, super-resolution, and deblurring. The comparison is done using two different types of generative models: diffusion models and flow models, and two different datasets: CelebA-HQ and ImageNet. The table shows the performance of each method for different sampling budgets (number of function evaluations, NFE), using three perceptual metrics: LPIPS (lower is better), KID (lower is better), and FID (lower is better).
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.
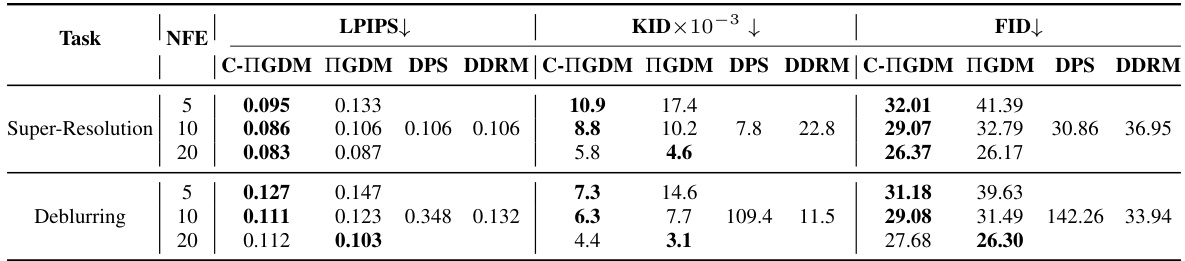
🔼 This table presents a comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against several baselines for solving noiseless linear inverse problems using diffusion and flow models. The comparison is done across different numbers of function evaluations (NFEs), a measure of computational cost. Results are shown for three inverse problems (Inpainting, Super-Resolution, and Deblurring) using both flow (CelebA-HQ dataset) and diffusion (ImageNet dataset) models. The best performing method for each NFE budget is highlighted in bold.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.

🔼 This table presents a comparison of the proposed Conditional Conjugate Integrators (C-IGDM and C-IGFM) against several baseline methods for solving noiseless linear inverse problems. The comparison is done across different sampling budgets (indicated by NFE - Number of Function Evaluations) and includes both flow-based (CelebA-HQ dataset) and diffusion-based (ImageNet dataset) models. The table shows quantitative metrics (LPIPS, KID, and FID) for each method and sampling budget. Bold entries highlight the best-performing method for each evaluation metric at a given budget.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.

🔼 This table presents a quantitative comparison of the proposed Conditional Conjugate Integrators (C-IG(D/F)M) against existing baselines for three different linear inverse problems: image super-resolution, inpainting, and Gaussian deblurring. The results are shown for both diffusion and flow models, trained on CelebA-HQ and ImageNet datasets respectively. The table displays the LPIPS, KID, and FID scores for different numbers of function evaluations (NFEs) representing sampling steps, allowing for a comparison of performance across different computational budgets. Bold values highlight the best-performing method for each task at a given NFE.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.
🔼 This table compares the performance of the proposed Conjugate IG(D/F)M methods against other baselines on noiseless linear inverse problems. It presents results for both flow models (using the CelebA-HQ dataset) and diffusion models (using the ImageNet dataset), showing quantitative metrics (LPIPS, KID, FID) at various sampling budgets (NFEs). The best performing method for each NFE is highlighted in bold.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.

🔼 This table presents a quantitative comparison of the proposed Conditional Conjugate Integrators (C-IGDM and C-IGFM) against existing baselines for various image restoration tasks (super-resolution, inpainting, and deblurring). The results are shown separately for flow-based models (CelebA-HQ dataset) and diffusion-based models (ImageNet dataset). Performance is evaluated across different sampling budgets (indicated by NFE), using metrics such as LPIPS, KID, and FID. Bold values highlight the best performance for each metric at each sampling budget.
read the caption
Table 1: Comparison between Conjugate IG(D/F)M and other baselines for noiseless linear inverse problems. Top: Flow models (CelebA-HQ) and Bottom: Diffusion Models (ImageNet). Entries in bold show the best performance for a given sampling budget.
Full paper#