Provable Tempered Overfitting of Minimal Nets and Typical Nets

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in deep learning and generalization theory. It provides novel theoretical results on the phenomenon of benign overfitting in deep neural networks, a topic of significant current interest. The findings challenge traditional understanding, offering new avenues for research into the generalization capabilities of deep NNs and influencing algorithm design. The paper’s results directly impact the ongoing discussions surrounding model selection, regularization, and the implicit bias of various training algorithms.

Visual Insights

#

This figure compares different overfitting behaviors (benign, tempered, catastrophic) of a binary classification model trained on a noisy dataset. The left panel shows the generalization error on the noisy dataset (D), while the right panel shows the generalization error on a clean dataset (D₀). The results illustrate how different noise models affect the generalization error and how the proposed models exhibit tempered overfitting.

In-depth insights

#

Tempered Overfitting

#

The concept of “tempered overfitting” offers a nuanced perspective on the generalization capabilities of deep neural networks (DNNs). It suggests that perfect interpolation of noisy training data, while seemingly at odds with traditional generalization theory, isn’t necessarily catastrophic. Instead, the generalization error can be far better than trivial, falling somewhere between benign and catastrophic overfitting. This research explores this phenomenon in DNNs with binary weights and activations, a setting relevant to resource-constrained applications. The authors establish theoretical results demonstrating tempered overfitting for both minimal-sized NNs and typical, randomly sampled, interpolating NNs. Their analysis reveals a dependency of the generalization error on the statistical properties of label noise, highlighting the importance of noise characteristics in understanding overfitting behavior. Importantly, these findings hold for deep NNs without requiring extremely high or low input dimensions, extending the understanding of benign overfitting beyond previously studied regimes.

Min-Size NN

#

The concept of “Min-Size NN” in the context of the research paper centers on investigating the overfitting behavior of neural networks (NNs) with the minimal number of weights. This approach directly tackles the trade-off between model complexity and generalization performance, a crucial aspect of machine learning. By focusing on minimal NNs, the study aims to determine if simplicity intrinsically leads to tempered overfitting, a scenario where generalization error is neither optimal nor catastrophic, but rather significantly better than trivial. This approach contrasts with studies focusing on heavily overparameterized NNs, offering a different perspective on overfitting’s nature. The core question explored is whether the inherent constraints of a minimal architecture encourage the NN to find solutions that generalize well, even in the presence of noise, demonstrating the potential of Occam’s razor in modern deep learning. The findings regarding min-size NN overfitting have implications for model selection, neural architecture search, and our understanding of the implicit biases driving generalization.

Random Interpolators

#

The concept of “Random Interpolators” in the context of deep learning is intriguing. It challenges the traditional understanding of generalization, where complex models trained on noisy data are expected to overfit. Random interpolators, in contrast, are models randomly selected from the set of all models that perfectly fit the training data. This approach is especially interesting because it sidesteps explicit regularization techniques or reliance on implicit biases within optimization algorithms. The research explores the generalization performance of these randomly chosen interpolators, which empirically demonstrates tempered overfitting - a generalization error that is neither catastrophic nor trivially benign. This unexpected result suggests that the capacity for generalization might be inherent to the model structure itself, rather than being solely dependent on learning algorithms or regularization. Studying random interpolators offers a unique lens for investigating the implicit biases and properties of neural network architectures, thereby improving our understanding of how neural networks generalize well despite over-parameterization and noisy data.

Generalization Bounds

#

The heading ‘Generalization Bounds’ likely refers to a section in the research paper that delves into the theoretical guarantees of a machine learning model’s ability to generalize to unseen data. The authors likely present mathematical bounds that constrain the model’s generalization error, providing insights into how well the model’s performance on training data translates to its performance on new, unseen data. These bounds might depend on factors such as the model’s complexity, the size of the training dataset, and the noise level in the data. A key aspect would be the relationship between the model’s empirical risk (error on training data) and its generalization error (error on unseen data), potentially showing a trade-off between model complexity and generalization performance. The results may demonstrate the existence of benign overfitting where models that perfectly fit noisy training data still generalize well, challenging classical intuitions. Specific techniques like VC-dimension or Rademacher complexity may be employed. The section’s significance lies in offering a theoretical understanding of the model’s behavior, complementing experimental results and potentially guiding model selection or design choices to improve generalization.

Future Research

#

The paper’s theoretical analysis of tempered overfitting in deep neural networks opens several exciting avenues for future research. Extending the results to more realistic network architectures, such as convolutional neural networks (CNNs) or recurrent neural networks (RNNs), is crucial for practical impact. The reliance on binary weights and threshold activations is a limitation; investigating the impact of more realistic weight distributions and activation functions is key. Exploring different learning rules beyond min-size and random interpolators, including those inspired by gradient-based methods, would provide deeper insights into the phenomenon. Finally, empirical validation is necessary to confirm the theoretical findings and to explore the regimes where tempered overfitting is most prominent. A detailed investigation into the influence of different noise models and their impact on generalization is also warranted. The current work focuses on binary classification; extending the theoretical framework to handle multi-class settings and other types of supervised learning tasks would be a valuable contribution.

More visual insights

#

More on figures

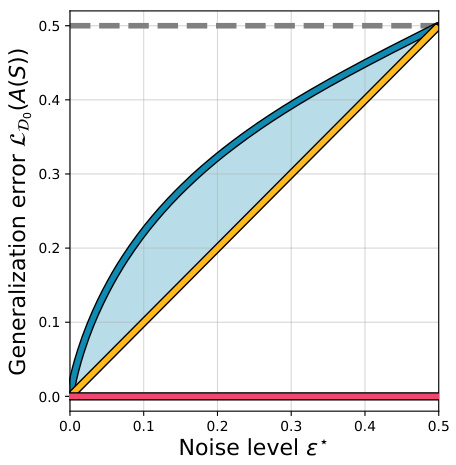
This figure illustrates different overfitting behaviors (benign, tempered, catastrophic) for deep neural networks trained on noisy datasets. The left panel shows generalization error on a noisy dataset (D), while the right panel shows generalization error on a clean dataset (D₀) derived from D. The results demonstrate that the generalization error is neither optimal nor trivial, indicating tempered overfitting, and that the type of overfitting behavior depends on the statistical properties of the label noise.

This figure illustrates how a neural network can interpolate a noisy dataset. It shows three networks: a teacher network (a), a network memorizing label flips (b), and a wider student network that combines the previous two networks and uses an XOR construction to perfectly memorize the training data. The color-coding of the edges helps to visualize how the parameters of the teacher and label flip memorization networks are integrated into the student network.

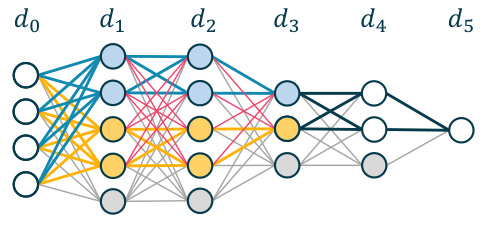
This figure illustrates how a neural network can interpolate a noisy dataset by combining the teacher network’s weights with a network that memorizes the noise. Blue edges represent weights identical to the teacher network, yellow edges represent weights memorizing the label flips, red edges have zero weight, and two XOR layers combine the outputs to create the interpolator.

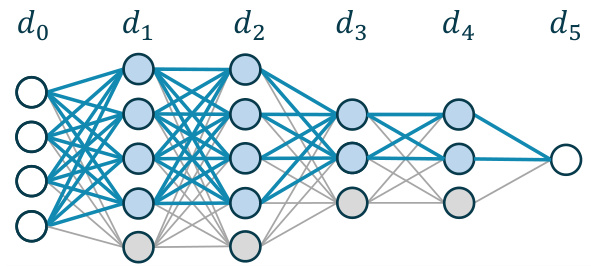
This figure illustrates how a noisy dataset can be interpolated using a neural network. It decomposes the task of interpolation into two subtasks: (1) matching the teacher network’s weights and (2) memorizing the noise (label flips). The figure shows how to use different subsets of the parameters (blue edges for teacher, yellow for noise) and how to use an XOR operation to merge these subsets. The result is a wider network that perfectly interpolates the noisy training data.

Full paper

#