Safe Exploitative Play with Untrusted Type Beliefs

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in multi-agent systems and game theory, addressing a critical gap in understanding the tradeoff between exploiting opportunities and managing risks arising from imperfect information. It provides novel theoretical frameworks for both normal-form and stochastic Bayesian games, offering valuable insights for designing robust and safe AI agents and guiding the development of more effective learning algorithms.

Visual Insights

#

This figure illustrates a stochastic Bayesian game. The left panel shows the agent interacting with an environment and opponents, having a belief about the opponent’s types (θ). The right panel depicts the tradeoff between trusting and distrusting those beliefs. Trusting leads to higher risk and opportunity while distrusting leads to lower risk and opportunity, highlighting the opportunity-risk tradeoff depending on the strategy (π) employed by the agent.

In-depth insights

#

Exploitative Play Tradeoffs

#

The concept of “Exploitative Play Tradeoffs” in multi-agent systems highlights the inherent tension between maximizing payoff by exploiting opponent weaknesses (exploitative play) and the risks associated with inaccurate beliefs about opponent types. Trusting learned beliefs about opponent types can lead to significant gains if accurate, but also substantial losses if the beliefs are wrong. Distrusting these beliefs leads to a more conservative approach, minimizing risk but potentially missing out on significant opportunities. This tradeoff is central to the design of effective agents. The optimal balance depends on several factors including the nature of the game (e.g., normal-form vs. stochastic Bayesian game), the quality of type prediction, and the agent’s risk tolerance. Formalizing this tradeoff often involves analyzing payoff gaps resulting from both correct and incorrect beliefs, characterized by metrics such as missed opportunity and risk. The challenge lies in finding strategies that provide a desirable balance between exploiting opportunities and mitigating risks. Research in this area focuses on developing algorithms and strategies that offer both safety and exploitability, with theoretical analysis establishing upper and lower bounds for performance in various game settings.

Untrusted Type Beliefs

#

The concept of “Untrusted Type Beliefs” in multi-agent systems is crucial because it acknowledges the inherent uncertainty in strategic interactions. Agents rarely possess perfect knowledge of their opponents’ types or behaviors. Instead, they must rely on predictions or beliefs, which may be inaccurate or outdated. This introduces a fundamental trade-off between risk and opportunity. Trusting these beliefs can lead to higher payoffs if correct, but significant losses if wrong. Conversely, distrusting beliefs leads to safer, more conservative strategies but potentially misses opportunities for greater gains. The research likely explores this trade-off formally, potentially by defining metrics to quantify opportunity (gain from exploiting incorrect beliefs) and risk (loss from acting on inaccurate beliefs). The analysis likely considers different game settings, like normal-form and stochastic games, and investigates strategies that optimally balance this trade-off, thereby leading to the development of robust and adaptive decision-making frameworks in uncertain environments.

Bayesian Game Analysis

#

Bayesian game analysis offers a powerful framework for modeling strategic interactions under uncertainty. It explicitly incorporates players’ beliefs about other players’ types and payoffs, leading to richer predictions than traditional game theory. Bayesian equilibrium, a central concept, represents a stable state where each player’s strategy is optimal given their beliefs and the strategies of others. However, the accuracy of beliefs is crucial. Incorrect beliefs can lead to suboptimal outcomes, highlighting the need for robust belief updating mechanisms. Analyzing the sensitivity of equilibrium strategies to belief perturbations helps assess the risk associated with strategic choices. Furthermore, Bayesian game analysis can be applied in various contexts, from economics and political science to cybersecurity and AI, providing a flexible tool for studying complex interactions in environments with incomplete information. The field is continuously evolving, with ongoing research focusing on computational methods for finding equilibria, developing dynamic models, and refining the treatment of information asymmetry and belief updating. The key to successful application lies in the ability to accurately model players’ beliefs and update them using available information, making Bayesian game analysis an exciting and relevant area for future research.

Stochastic Game Dynamics

#

Stochastic game dynamics investigates systems where multiple agents make decisions in an environment with inherent randomness. This contrasts with deterministic game theory, where outcomes are entirely predictable given player actions. Key features include probabilistic transitions between states, reflecting uncertainty in the system’s evolution, and the agents’ imperfect information about the environment or other players’ actions. The inherent uncertainty introduces significant complexity, making it challenging to predict long-term outcomes. Analyzing stochastic games often involves finding optimal strategies or equilibrium behavior under various assumptions about the agents’ rationality and knowledge. These strategies frequently involve managing risk and uncertainty, trading off potential high rewards against the possibility of negative consequences due to chance events. Different solution concepts and algorithms exist, such as Markov perfect equilibria or reinforcement learning methods, tailored to specific types of stochastic games and agent characteristics. The field draws upon concepts from probability theory, control theory, and computer science, offering valuable insights into modeling and analyzing many real-world dynamic systems such as competition in markets, human-robot interaction, and ecological processes.

Future Research

#

Future research directions stemming from this work on safe exploitative play could focus on several key areas. Extending the theoretical framework to handle time-varying type beliefs is crucial, moving beyond stationary assumptions to reflect real-world dynamics where opponent behavior changes over time. This requires more sophisticated modeling techniques and learning algorithms. Investigating the impact of incomplete or noisy type information is another vital direction. Real-world data is rarely perfect, and understanding how uncertainty affects the opportunity-risk tradeoff is essential for practical applications. Exploring the design of more robust and adaptive strategies that can handle such uncertainty is a significant challenge. The development of efficient algorithms that can learn and adapt quickly in dynamic environments, possibly incorporating techniques from online learning and reinforcement learning, would be particularly valuable. Further work could also examine how the results generalize to different game classes and more complex multi-agent systems. The current analysis primarily focuses on normal-form and stochastic Bayesian games; broadening the scope to consider other game structures and agent interactions would enhance the practical impact. Finally, rigorous empirical validation across diverse application domains is needed to confirm the theoretical findings and demonstrate the effectiveness of proposed strategies in real-world settings. This could involve case studies in areas like cybersecurity, economics, or robotics, where understanding and leveraging the opportunity-risk tradeoff is critical.

More visual insights

#

More on figures

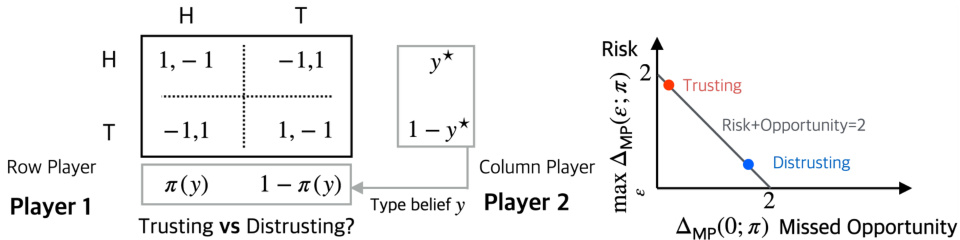
The figure on the left shows the payoff matrix for the Matching Pennies game. Player 1 has a belief about Player 2’s strategy (represented by y). Player 1 chooses a strategy (π(y)) aiming to maximize their payoff. The right side illustrates the tradeoff between opportunity (gain when beliefs are correct) and risk (loss from incorrect beliefs). The line represents the Pareto frontier, where any improvement in opportunity necessitates an increase in risk, and vice versa.

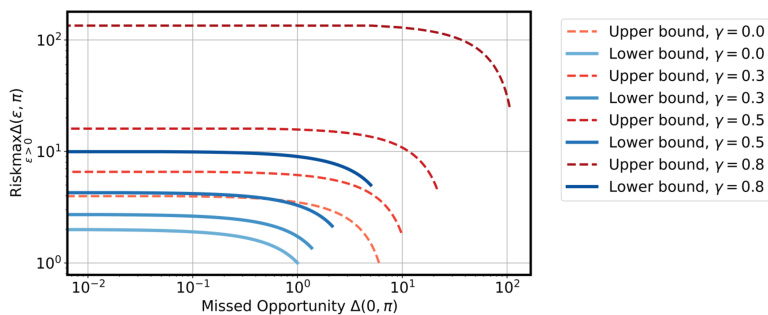
This figure displays the comparison between theoretical upper and lower bounds on the opportunity-risk tradeoff for stochastic Bayesian games, with varying discount factors (γ). The x-axis represents the missed opportunity (a measure of how far the strategy is from optimal when beliefs are correct), and the y-axis represents the maximum risk (the worst-case payoff difference due to incorrect beliefs). The different curves correspond to various discount factors, demonstrating how this tradeoff changes based on the discount factor.

The figure illustrates a stochastic Bayesian game where an agent interacts with an environment and opponents. The agent holds beliefs (θ) about the types of opponents. The right panel shows the tradeoff between trusting these beliefs versus distrusting them. Trusting leads to higher risk and opportunity, while distrusting leads to lower risk and opportunity. The overall relationship demonstrates an opportunity-risk tradeoff that varies according to the strategy (π) employed by the agent.

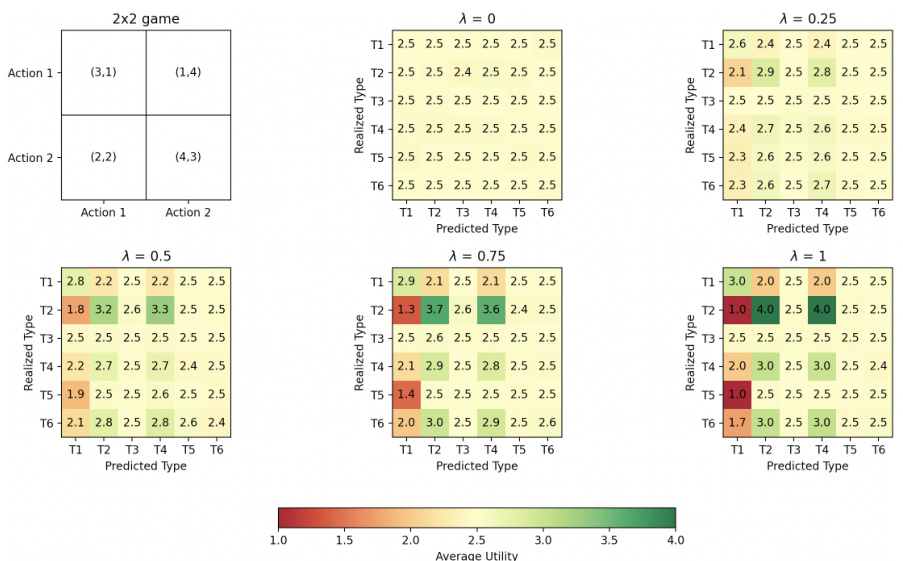
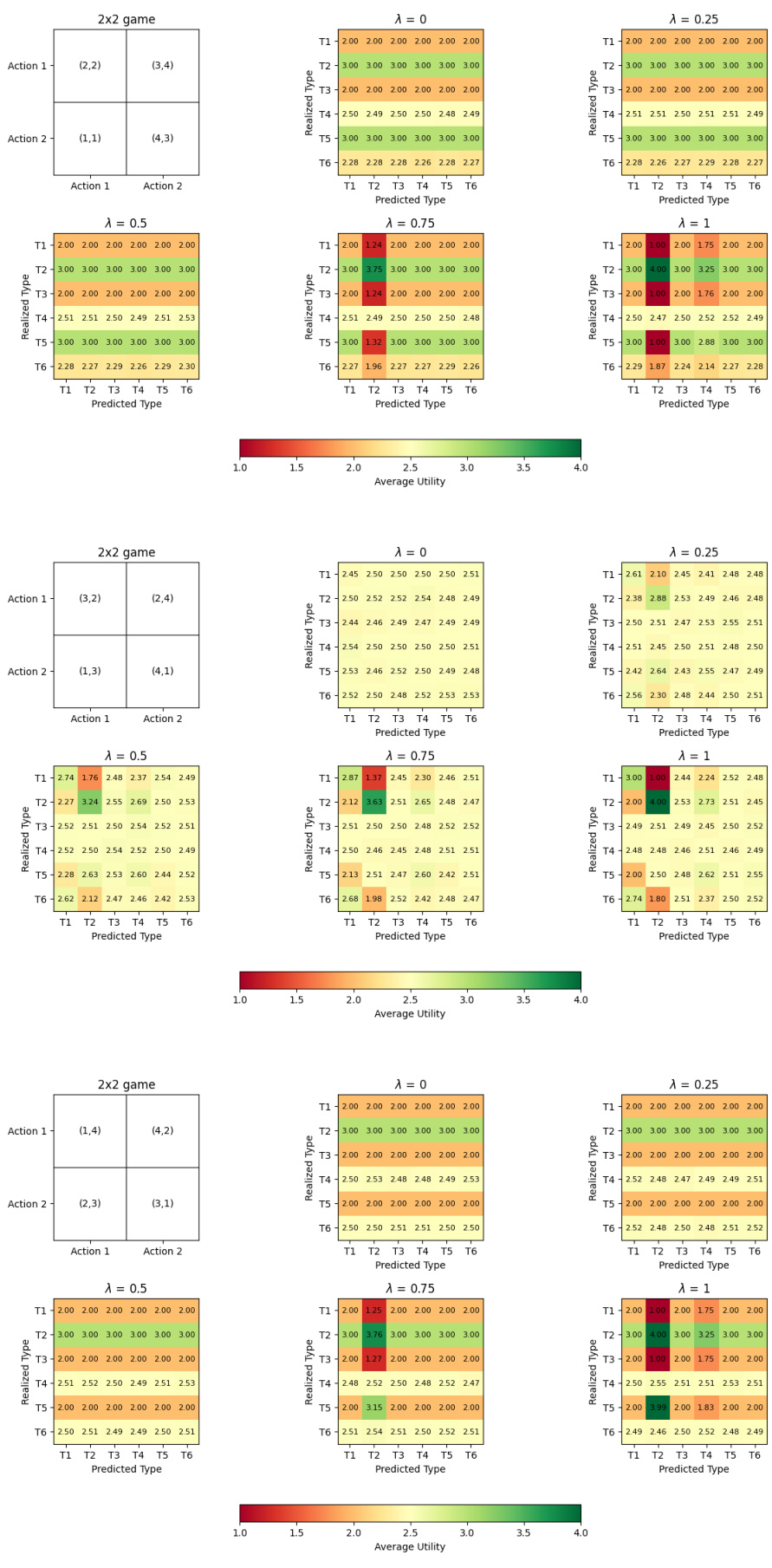
The left panel shows the 78 2x2 games used in the case study. The right panel shows the opportunity-risk tradeoff for one of those games. The tradeoff is evaluated using an algorithm that varies its trust (λ) in type beliefs. When trust is high (λ=1), the algorithm uses a best response strategy, resulting in higher risk and opportunity. When trust is low (λ=0), the algorithm uses a minimax strategy, resulting in lower risk and opportunity. The plot shows the average results from 1000 random runs, illustrating the variability of the results.

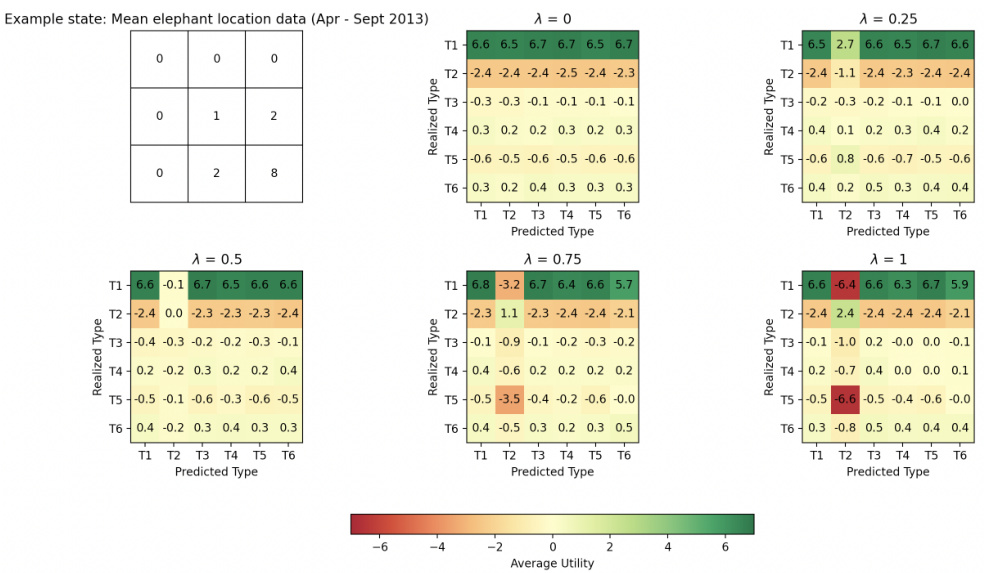
The figure illustrates a stochastic Bayesian game where an agent makes decisions based on its belief of the types of other agents. The left panel shows the game’s structure, where an agent interacts with an environment and opponents, having a belief about their types (θ ∈ Θ). The right panel shows the tradeoff between trusting and distrusting these beliefs. Trusting the beliefs leads to higher risk but also higher potential opportunity. Distrusting the beliefs results in lower risk and a lower potential opportunity. This visualizes the central concept of the paper: the fundamental tradeoff between risk and opportunity when dealing with uncertain type beliefs in strategic interactions.

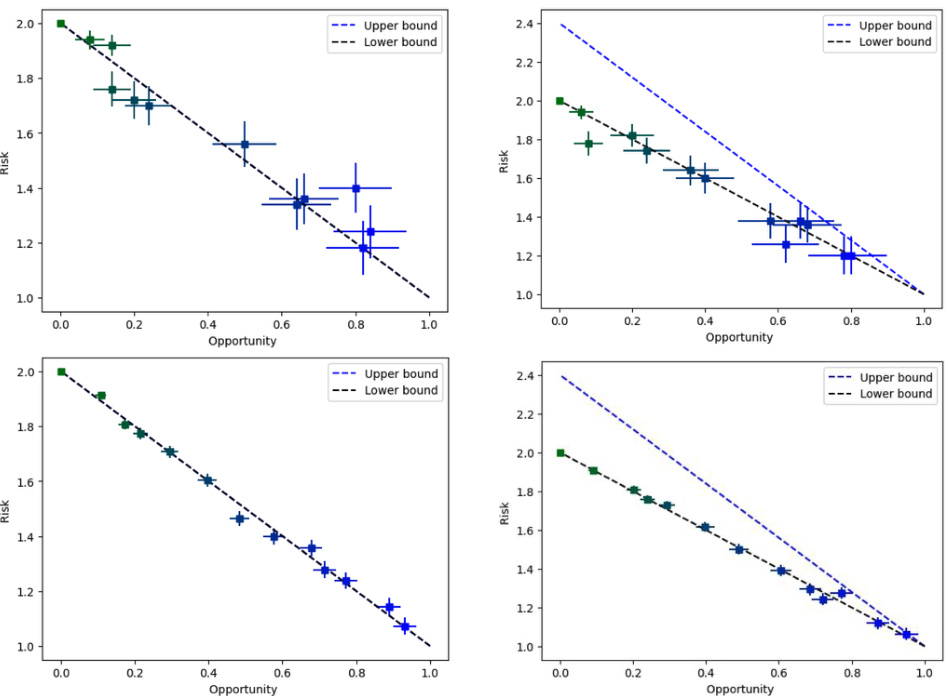
This figure shows the comparison of lower and upper bounds on the opportunity-risk tradeoff for stochastic Bayesian games with varying discount factors (γ). The x-axis represents the missed opportunity, and the y-axis represents the risk. Different curves represent different values of γ, illustrating how the tradeoff changes as γ varies. The figure is a visual representation of the theoretical results presented in Theorem 4.1 and 4.2, showing the relationship between opportunity (missed opportunity) and risk (worst-case payoff difference) in stochastic games.

This figure compares the theoretical lower and upper bounds on the opportunity-risk tradeoff derived in Theorems 4.1 and 4.2, respectively, for stochastic Bayesian games. The x-axis represents the missed opportunity (Δ(0; π)), while the y-axis represents the risk (maxε>0 Δ(ε; π)). Different curves show the bounds for varying discount factors (γ). The figure shows how the opportunity-risk tradeoff changes as the discount factor varies, illustrating the impact of the time horizon on the agent’s strategic choices in the face of uncertainty about opponent types.

The figure on the left shows a diagram of a stochastic Bayesian game. There is an agent who interacts with an environment and opponents. The agent has beliefs about the types of the opponents. The figure on the right shows the opportunity-risk tradeoff that the paper examines. The y-axis represents the risk, and the x-axis represents the missed opportunity. The curve shows the Pareto frontier, which is the set of all points that are Pareto optimal. A Pareto optimal point is a point where it is not possible to improve one objective without worsening another.

Full paper

#