↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Machine learning models often struggle with out-of-distribution (OOD) data, failing to generalize to unseen data or misclassify novel instances. This poses significant challenges in real-world applications that demand robust and reliable models. Existing research often tackles OOD generalization and detection separately, lacking a unified theoretical understanding and practical approach.
This paper introduces a novel graph-theoretic framework that integrates OOD generalization and detection. Using graph factorization, it derives data representations allowing theoretical error quantification for both tasks. Experiments show the method’s effectiveness, outperforming existing approaches in both OOD generalization and detection. The framework provides theoretical backing and achieves practically competitive results, addressing a crucial gap in robust machine learning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in machine learning and related fields because it addresses the critical challenge of out-of-distribution (OOD) generalization and detection in real-world applications. By introducing a novel graph-theoretic framework and providing theoretical guarantees, the paper significantly advances the state-of-the-art and opens doors for future research directions in robust and reliable machine learning models. The joint approach to OOD generalization and detection is highly relevant to the current trends, and the theoretical guarantees make it particularly valuable.
Visual Insights#
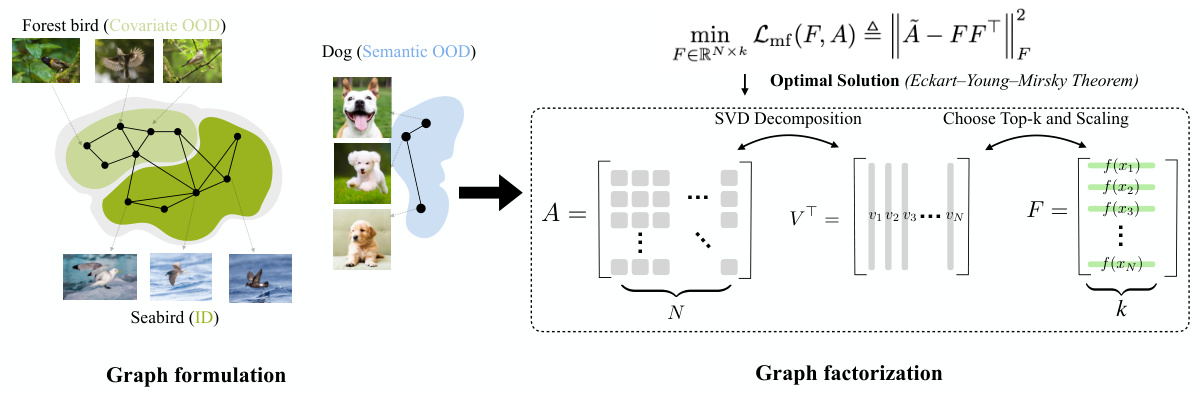
This figure illustrates the proposed graph-theoretic framework for jointly addressing out-of-distribution (OOD) generalization and detection. The left panel shows the graph formulation, where nodes represent data points (in-distribution (ID), covariate OOD, and semantic OOD) and edges connect similar data points. The right panel details the graph factorization process, using singular value decomposition (SVD) to obtain data representations from the adjacency matrix which allows for quantifying errors in OOD generalization and detection.
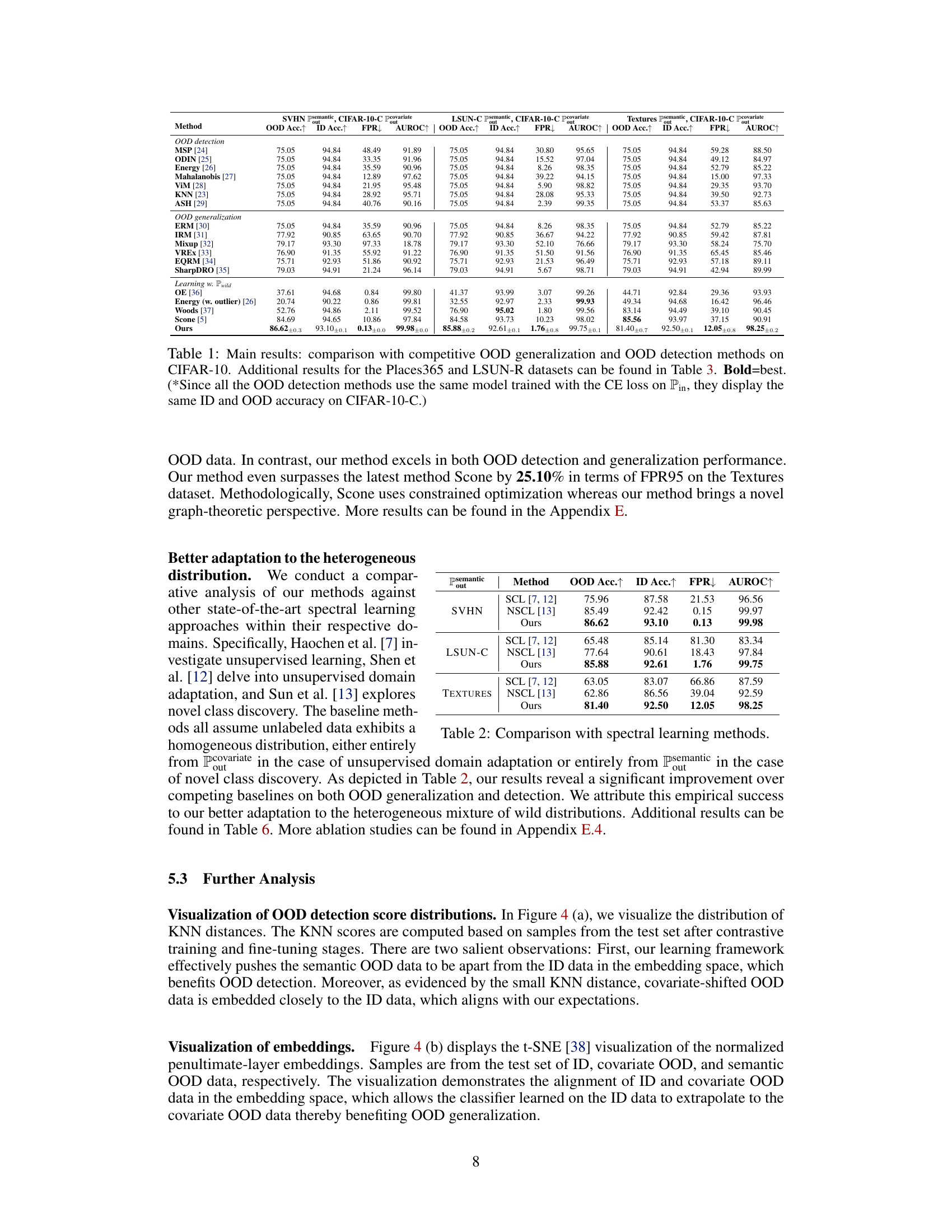
This table presents the main results of the proposed graph-based framework for OOD generalization and detection. It compares the performance of the proposed method against several state-of-the-art methods for OOD generalization and detection on the CIFAR-10 dataset. The table includes metrics for ID generalization accuracy, OOD generalization accuracy, and OOD detection performance (FPR and AUROC). The results show that the proposed method achieves competitive performance compared to existing baselines in terms of both OOD generalization and detection, particularly in terms of low false positive rates (FPR). Additional results are referenced for other datasets in table 3.
In-depth insights#
Graph OOD#
The concept of “Graph OOD” presents a novel approach to out-of-distribution (OOD) detection and generalization by leveraging graph-theoretic methods. Instead of treating data points as isolated entities, this framework models data as a graph where nodes represent data points and edges quantify their similarity, potentially incorporating both labeled and unlabeled data. This allows the algorithm to capture complex relationships and dependencies within the data. Graph factorization techniques, such as spectral decomposition, are used to derive low-dimensional data representations, facilitating the analysis of OOD generalization and detection performance. The method’s strength lies in its ability to provide provable error bounds, offering theoretical guarantees for OOD performance. This approach contrasts with traditional methods by providing a more holistic and theoretically grounded understanding of OOD, bridging the gap between separate OOD detection and generalization tasks. By using graph structures, the method effectively handles diverse data shifts, improving on existing methods which may struggle with high heterogeneity and uncertainty in real-world data. The efficacy of this approach is further supported by competitive empirical results, demonstrating its value as a practical and robust solution for OOD problems.
Spectral Learning#
Spectral learning, in the context of this research paper, leverages graph spectral methods to derive data representations. This approach begins by constructing a graph where nodes represent data points and edge weights reflect similarity. Spectral decomposition of the graph’s adjacency matrix is then performed to obtain low-dimensional embeddings, effectively capturing the underlying data structure. These embeddings are crucial for tackling both out-of-distribution (OOD) generalization and detection. The method’s strength lies in its ability to provide theoretical guarantees on performance, quantifying errors for both generalization and detection. Closed-form solutions are derived for error metrics, offering a rigorous theoretical framework. Moreover, the approach offers practical advantages; the spectral decomposition can be achieved through efficient optimization using neural networks, bridging theory and practice. The effectiveness is empirically demonstrated, showcasing improvements over existing state-of-the-art methods.
OOD Generalization#
Out-of-distribution (OOD) generalization focuses on a model’s ability to maintain accuracy when encountering data that differs from its training distribution. This is crucial for real-world applications where data inevitably shifts. Covariate shift, where the input distribution changes but the underlying relationship remains the same, and semantic shift, where the relationship itself changes, are key challenges. Effective OOD generalization often requires learning domain-invariant features that capture underlying concepts rather than solely relying on training data specifics. Approaches may involve techniques like domain adaptation to bridge training and test distribution gaps, robust optimization to handle distributional uncertainty, or meta-learning to learn generalization strategies. The effectiveness of these approaches is deeply tied to understanding and mitigating the impact of data shifts, highlighting the need for methods that learn robust and generalizable features to ensure reliable performance across various data conditions.
OOD Detection#
Out-of-distribution (OOD) detection is a crucial aspect of robust machine learning, focusing on a model’s ability to identify inputs that differ significantly from its training data. Effective OOD detection is vital for preventing unreliable predictions and ensuring system safety, particularly in real-world applications where unexpected data is common. The paper explores the problem through a graph-theoretic lens, proposing a novel framework that combines OOD detection with generalization. This approach leverages graph factorization to obtain data representations, enabling a theoretical analysis and quantification of OOD detection performance. The method’s strength lies in its ability to handle both covariate and semantic shifts, representing a significant advancement over traditional methods that often address these aspects separately. Empirical results demonstrate its effectiveness, offering competitive performance compared to state-of-the-art techniques. The theoretical underpinnings, coupled with the empirical validation, establish a strong foundation for future research in robust machine learning.
Future Work#
The paper’s omission of a dedicated “Future Work” section is notable. However, considering the research’s focus on bridging OOD detection and generalization using a graph-theoretic framework, several promising avenues emerge. Extending the framework to handle various data shift types beyond covariate and semantic shifts (e.g., concept drift, prior probability shift) would significantly enhance its applicability and robustness. Furthermore, exploring different graph construction methods and comparing their impact on performance is crucial. Investigating alternative graph representations beyond spectral decomposition and analyzing the theoretical properties of these approaches warrant further research. Integrating the proposed framework into existing OOD detection methods could potentially improve their overall performance. Finally, empirical validation on larger, more diverse datasets, and a more thorough comparison with advanced baselines are needed to firmly establish the method’s advantages. Addressing these points could further solidify the theoretical grounding and practical impact of the presented approach.
More visual insights#
More on figures
This figure illustrates the graph-theoretic framework proposed in the paper for jointly addressing out-of-distribution (OOD) generalization and detection. The left panel shows the graph formulation, where nodes represent data points (in-distribution (ID), covariate-shifted OOD, and semantic-shifted OOD) and edges represent relationships between data points. The right panel depicts the graph factorization process, which involves singular value decomposition (SVD) of the adjacency matrix to obtain data representations. These representations are then used to quantify OOD generalization and detection performance through provable error bounds. The overall framework combines graph-based data representation with spectral analysis to bridge the gap between OOD generalization and detection.
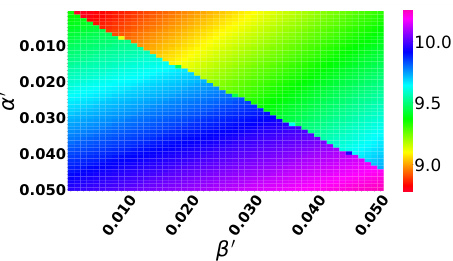
This figure shows a heatmap visualizing the value of function S(f) across different values of α’ and β’. The function S(f) quantifies the distance between ID and semantic OOD data, with larger values indicating better OOD detection capability. The heatmap reveals the relationship between these two parameters and their impact on the separability of ID data from semantic OOD data, offering insights into the effectiveness of OOD detection. The color intensity represents the magnitude of S(f).
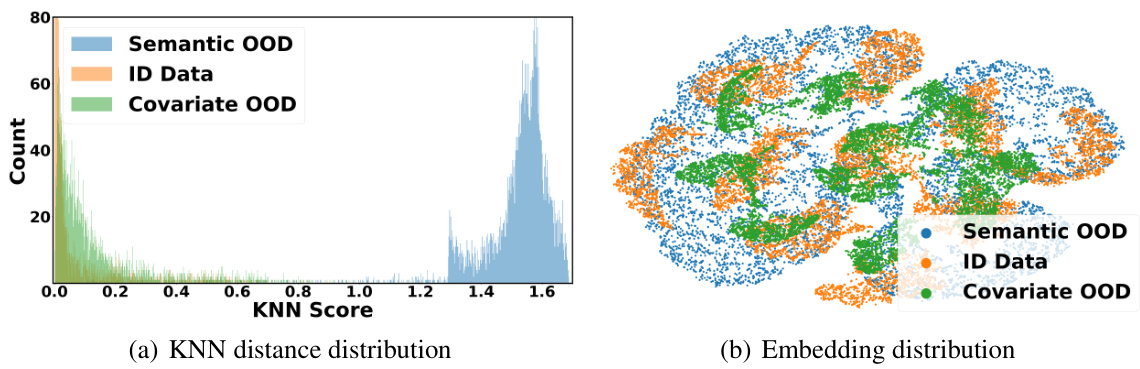
This figure visualizes the distribution of KNN distances and the t-SNE visualization of learned embeddings, which are used to analyze the performance of the proposed graph-theoretic framework. Panel (a) shows the distribution of KNN distances for the ID data, covariate OOD, and semantic OOD data. The distribution of KNN distances clearly shows the separation between semantic OOD data and the ID data, while the covariate OOD data is embedded closely to the ID data. Panel (b) shows the t-SNE visualization of learned embeddings, demonstrating the grouping of ID and covariate OOD data in the embedding space while semantic OOD data is separated. This visualization supports the theoretical analysis and empirical results presented in the paper.
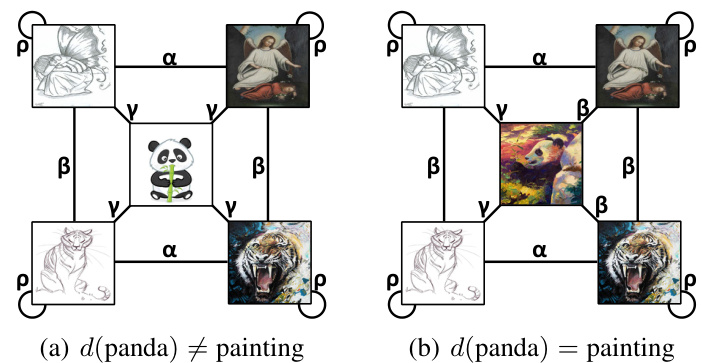
This figure illustrates the proposed graph-theoretic framework. The left panel shows the graph formulation with three data types: in-distribution (ID), covariate out-of-distribution (OOD), and semantic OOD. The right panel depicts the graph factorization process used to obtain data representations for quantifying OOD generalization and detection performance. The graph factorization uses singular value decomposition (SVD) to obtain a low-rank approximation of the adjacency matrix, allowing for the derivation of closed-form solutions which are then used to quantify error in both generalization and detection.

The figure shows the heatmap of function S(f) which represents the separability between ID and semantic OOD data. The magnitude of S(f) reflects the extent of separation between ID and semantic OOD data. Larger S(f) suggests better OOD detection capability. The x-axis represents α’ and the y-axis represents β’, which are parameters related to the augmentation transformation probability. The color bar represents the value of S(f). The heatmap shows how the separability varies depending on the values of α’ and β'.
More on tables
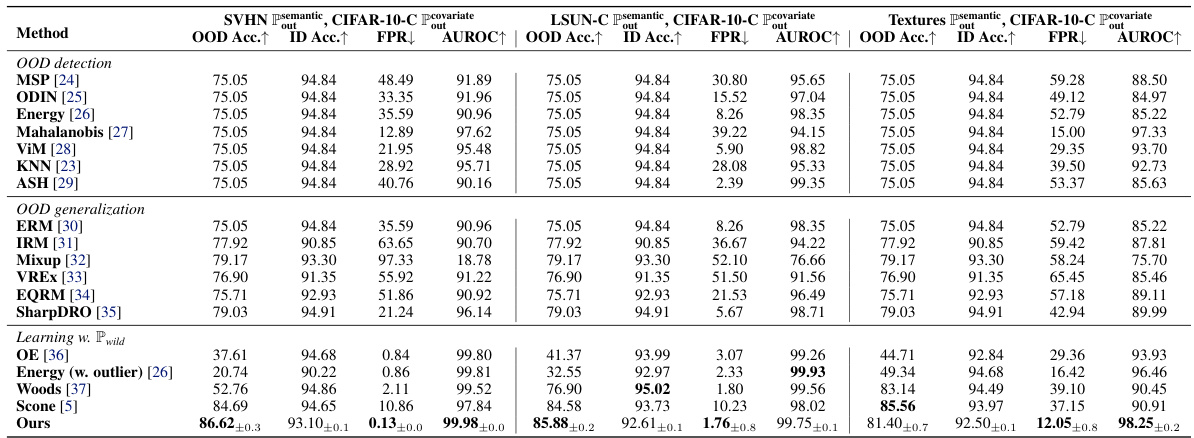
This table presents the main results of the paper, comparing the proposed graph-based method with several state-of-the-art techniques for out-of-distribution (OOD) generalization and detection on the CIFAR-10 dataset. It shows the ID accuracy, OOD accuracy, false positive rate (FPR), and area under the ROC curve (AUROC) for each method. The table highlights the competitive performance of the proposed method, particularly its strong OOD generalization capability and low FPR, indicating its effectiveness in distinguishing between in-distribution and out-of-distribution data. It also notes that the ID and OOD accuracy values are the same for several methods due to them using the same model trained with cross-entropy loss.

This table compares the proposed method with other state-of-the-art spectral learning methods on three semantic-shift OOD datasets: SVHN, LSUN-C, and TEXTURES. The comparison highlights the superior performance of the proposed method in terms of OOD accuracy, ID accuracy, FPR (false positive rate), and AUROC (area under the receiver operating characteristic curve). The results demonstrate the effectiveness of the proposed graph-based framework in handling heterogeneous data distributions.
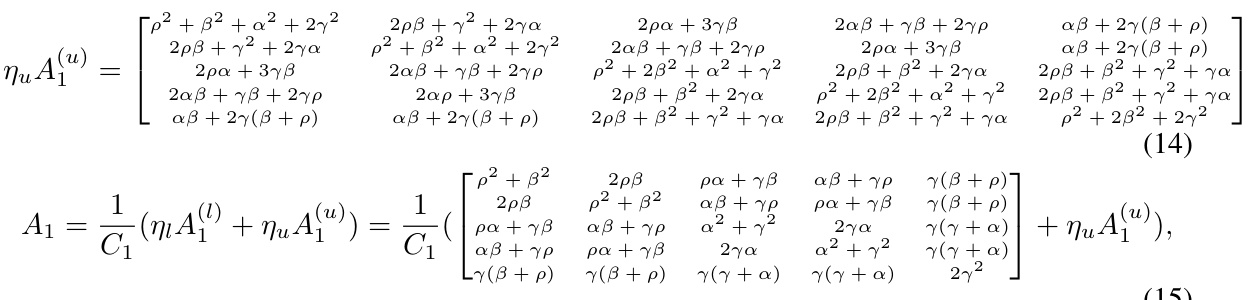
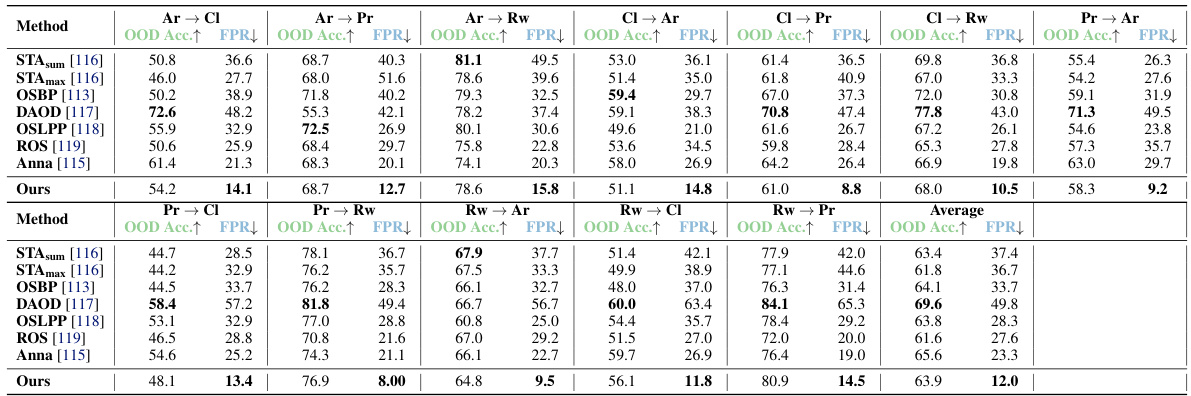
This table presents the main results of the paper, comparing the proposed graph-based method with several state-of-the-art approaches for out-of-distribution (OOD) generalization and detection on the CIFAR-10 dataset. It shows the performance of various methods across three key metrics: ID generalization accuracy, OOD generalization accuracy, and OOD detection error (FPR). The table highlights the competitive performance of the proposed method in both OOD generalization and OOD detection, outperforming many baselines, especially in terms of false positive rate.

This table presents a comparison of the proposed method’s performance against various state-of-the-art methods for out-of-distribution (OOD) generalization and detection on the CIFAR-10 dataset. The table includes results for OOD detection methods (MSP, ODIN, Energy, Mahalanobis, ViM, KNN, ASH), OOD generalization methods (ERM, IRM, Mixup, VREX, EQRM, SharpDRO), and methods trained with wild data (OE, Energy (w/ outlier), Woods, Scone). The table shows the OOD accuracy, ID accuracy, false positive rate (FPR), and area under the receiver operating characteristic curve (AUROC) for each method. The proposed method’s results (Ours) are highlighted in bold, indicating superior performance.

This table presents the results of the proposed method and baselines on the ImageNet-100 dataset for OOD generalization and detection. The in-distribution data (Pin) is ImageNet-100, covariate-shifted OOD data (Pcovariate) is ImageNet-100-C with Gaussian noise, and semantic-shifted OOD data (Psemantic) is iNaturalist. The table shows the OOD Accuracy, In-distribution Accuracy, False Positive Rate (FPR), and Area Under the ROC Curve (AUROC) for each method. The method with the highest OOD accuracy is highlighted in bold.
This table presents the main experimental results comparing the proposed graph-based method against various state-of-the-art techniques for out-of-distribution (OOD) generalization and detection on the CIFAR-10 dataset. It provides a quantitative comparison across multiple metrics, including OOD accuracy, in-distribution accuracy, false positive rate, and area under the ROC curve (AUROC). The results show that the proposed method achieves competitive performance, especially excelling in OOD detection. Additional results on Places365 and LSUN-R datasets are available in Table 3.
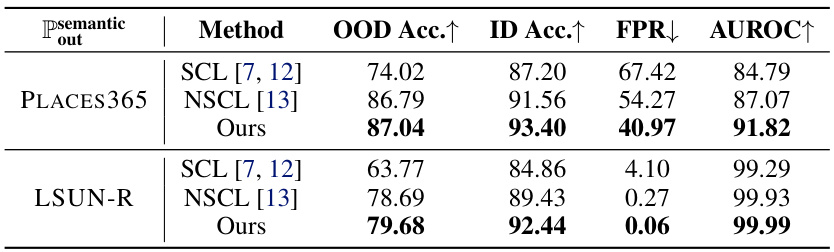
This table compares the proposed graph-based method with other state-of-the-art spectral learning approaches. The comparison is done using two semantic OOD datasets: PLACES365 and LSUN-R. The metrics used for comparison are OOD generalization accuracy, ID accuracy, false positive rate (FPR), and area under the ROC curve (AUROC). The results highlight that the proposed method outperforms the other methods, especially in terms of FPR, demonstrating its ability to better distinguish between in-distribution and out-of-distribution samples.
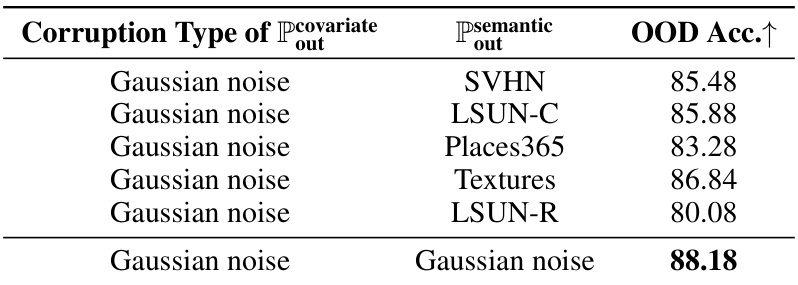
This table shows the impact of semantic OOD data on the generalization ability of the model. It explores the effect of whether the semantic OOD data shares the same domain as the covariate OOD data. The results indicate that when semantic OOD shares the domain as covariate OOD, the performance is significantly improved.

This table presents the main results of the proposed graph-based framework for OOD generalization and detection, comparing its performance against various state-of-the-art methods on the CIFAR-10 dataset. The table shows the ID accuracy, OOD accuracy (for both covariate and semantic shifts), false positive rate (FPR), and area under the ROC curve (AUROC) for each method. It highlights the competitive performance of the proposed approach in both OOD generalization and detection tasks, excelling in FPR95 compared to other state-of-the-art methods. Additional results using the Places365 and LSUN-R datasets are provided in Table 3.

This table presents the main results of the paper, comparing the proposed graph-based method with various state-of-the-art methods for both OOD generalization and detection on the CIFAR-10 dataset. The table includes metrics such as OOD accuracy, ID accuracy, false positive rate (FPR), and area under the ROC curve (AUROC) for different semantic and covariate shift OOD datasets. The results showcase the competitive performance of the proposed method in comparison to existing baselines. It indicates that the proposed method excels in both OOD detection and generalization performance, outperforming existing methods on several metrics across multiple datasets.
Full paper#