↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reconstructing 3D surfaces from multiple images is a key challenge in computer vision. Existing methods often use neural radiance fields (NeRFs) or meshes, but these can be computationally expensive or lack detail. 3D Gaussian splatting offers a promising alternative, but existing approaches struggle to accurately infer signed distance functions (SDFs) due to the discrete and sparse nature of the Gaussians. They also suffer from off-surface drift, leading to incomplete or inaccurate surface representations.
This paper introduces a novel method that combines 3D Gaussian splatting with neural SDFs. The key is a differentiable “pulling” operation that dynamically aligns the 3D Gaussians to the zero-level set of the neural SDF. This ensures better alignment with the actual surface and makes the inference process more robust. The method uses both RGB and geometry constraints during optimization, improving the accuracy, smoothness, and completeness of the reconstructed surfaces. Experimental results demonstrate superior performance compared to state-of-the-art methods.
Key Takeaways#
Why does it matter?#
This paper is significant because it presents a novel method for inferring signed distance functions (SDFs) using 3D Gaussian splatting, improving the accuracy and efficiency of 3D surface reconstruction. It directly addresses the limitations of existing methods that struggle with the discrete and sparse nature of 3D Gaussians. This work also opens new avenues for research in differentiable rendering and implicit surface representation, potentially leading to significant advancements in various computer vision applications.
Visual Insights#
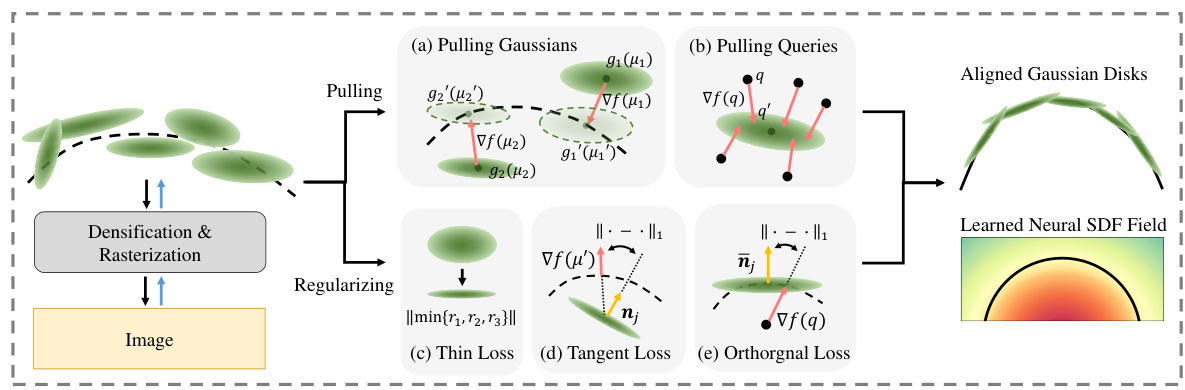
This figure illustrates the key steps of the proposed method. It shows how 3D Gaussians are pulled onto the zero-level set of a neural SDF (Signed Distance Function), using a differentiable pulling operation. This alignment improves accuracy in surface reconstruction. Neighboring space is also pulled to refine the SDF. Three constraints are used to regularize the process: ensuring Gaussians become thin disks, aligning these disks to the tangent plane of the zero-level set, and constraining query points to be pulled along the shortest path to the Gaussian disk. Finally, these steps are combined with differentiable rasterization to produce high-quality renderings and improve the inference of the Neural SDF.

This table presents a quantitative comparison of different methods for 3D surface reconstruction on the DTU dataset. The metric used is Chamfer Distance (CD), a measure of the geometric difference between the reconstructed surface and the ground truth. Lower CD values indicate better reconstruction accuracy. The table shows the average CD across multiple scenes in the DTU dataset, with best results highlighted for each scene and overall mean.
In-depth insights#
3D Gaussian Splatting#
3D Gaussian splatting is a novel technique in neural volume rendering that represents scenes using a set of 3D Gaussian functions. Each Gaussian is characterized by parameters such as position, variance, color, and opacity, offering a flexible and efficient way to model complex shapes and appearances. The key advantage lies in its differentiability, enabling gradient-based optimization for improved rendering quality and faster training compared to traditional methods like ray marching in Neural Radiance Fields (NeRFs). However, the discrete and sparse nature of the Gaussians presents challenges for surface reconstruction. The Gaussians’ uneven distribution and tendency to drift off surfaces hinder accurate surface inference. Therefore, effective strategies are needed to seamlessly integrate 3D Gaussian splatting with implicit surface representations (like Signed Distance Functions, SDFs) to leverage both the rendering efficiency of Gaussians and the continuous, implicit representation of SDFs. Methods addressing this gap focus on aligning Gaussians to surfaces and refining the SDF representation based on Gaussian properties. This integration resolves the challenges posed by the discrete nature of Gaussian splatting, allowing for high-quality rendering and accurate, continuous geometry reconstruction.
Neural SDF Inference#
Neural SDF inference combines the power of neural networks with the efficiency of signed distance functions (SDFs) for 3D shape representation. The core idea is to leverage neural networks’ ability to learn complex functions from data to predict the SDF of a 3D object. This approach offers several advantages: it can handle complex geometries that might be difficult to represent explicitly; it implicitly represents surfaces with high resolution, making it suitable for detailed reconstruction; and it offers a smooth and continuous representation of surfaces unlike meshes or point clouds. The inference process usually involves training the neural network on data such as multi-view images or point clouds to learn a mapping from coordinates in 3D space to the corresponding signed distances. A key challenge in neural SDF inference is the efficient and accurate estimation of the SDF, especially for complex shapes with fine details. Various techniques, including differentiable rendering and implicit surface representation learning, are employed to address this issue. The effectiveness of this approach is greatly impacted by the choice of network architecture, loss function, data quality, and training methodology. The resulting SDF can then be used for various downstream tasks like 3D shape reconstruction, novel view synthesis, and collision detection.
Differentiable Pulling#
Differentiable pulling, in the context of neural implicit surface reconstruction using 3D Gaussian splatting, is a crucial technique for effectively aligning the discrete Gaussian primitives with the continuous implicit surface represented by the neural signed distance function (SDF). It’s a differentiable process, meaning that gradients can be computed, enabling backpropagation during training. This allows for the simultaneous optimization of both the 3D Gaussians’ parameters and the neural SDF’s weights. The process involves dynamically adjusting the position of each Gaussian so that its center lies on the zero-level set of the SDF, thereby ensuring a consistent and accurate representation of the surface. The gradients of the SDF provide a direction for moving each Gaussian, and the magnitude of the gradient influences the distance moved. Differentiable pulling improves training efficiency by directly linking the Gaussian’s position to the implicit surface representation and facilitating the flow of gradient information between the two. This avoids costly post-processing steps like mesh extraction and enhances the accuracy and completeness of the final surface reconstruction.
Multi-view Consistency#
Multi-view consistency, in the context of 3D reconstruction from multiple images, refers to the constraint that the reconstructed model should be consistent with all available views. This means that the projections of the 3D model onto each camera’s image plane should accurately match the observed 2D image data. Achieving multi-view consistency is crucial for creating accurate and reliable 3D models, as inconsistencies indicate errors in the reconstruction process. Several techniques are used to enforce multi-view consistency, including minimizing photometric errors (differences in pixel color between rendered and real images), geometric errors (differences in 3D point positions from different views), and leveraging techniques like photogrammetry and structure from motion (SfM). The degree to which multi-view consistency is achieved often determines the quality and reliability of the final 3D reconstruction. A high degree of consistency suggests that the 3D model accurately represents the scene captured in the images; low consistency, however, indicates inaccuracies and the potential need for refinement. The challenge lies in balancing the enforcement of multi-view consistency with other factors, such as computational cost and the robustness to noise or occlusion in individual views. Methods employing neural networks, in particular, must carefully manage this trade-off between accuracy and efficiency.
Future Enhancements#
Future enhancements for this research could involve exploring alternative implicit representation techniques beyond signed distance functions (SDFs), such as occupancy fields or radiance fields, to potentially address limitations in representing intricate surface details or handling transparency. Investigating more sophisticated Gaussian splatting methods or incorporating multi-resolution techniques could also improve efficiency and accuracy, especially for complex scenes. Furthermore, adaptive sampling strategies could enhance performance by focusing computational resources on regions requiring higher fidelity. Finally, applying this framework to dynamic scenes or incorporating semantic information during reconstruction are promising avenues for broadening the scope and applicability of the approach.
More visual insights#
More on figures
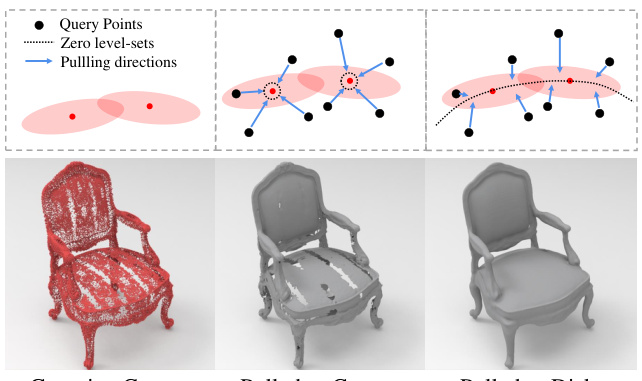
This figure illustrates the core pipeline of the proposed method for neural signed distance function (SDF) inference through 3D Gaussian splatting. It shows how 3D Gaussians are pulled onto the zero-level set of the SDF (a) for rendering and (b) for SDF refinement. Three constraints are introduced to improve the accuracy and smoothness of the resulting SDF, namely: (c) enforcing thin disk shapes for the Gaussians, (d) aligning the disk tangent to the zero-level set’s surface normal, and (e) pulling query points along the shortest path towards the Gaussian disk. The bottom row shows examples of the reconstruction process.

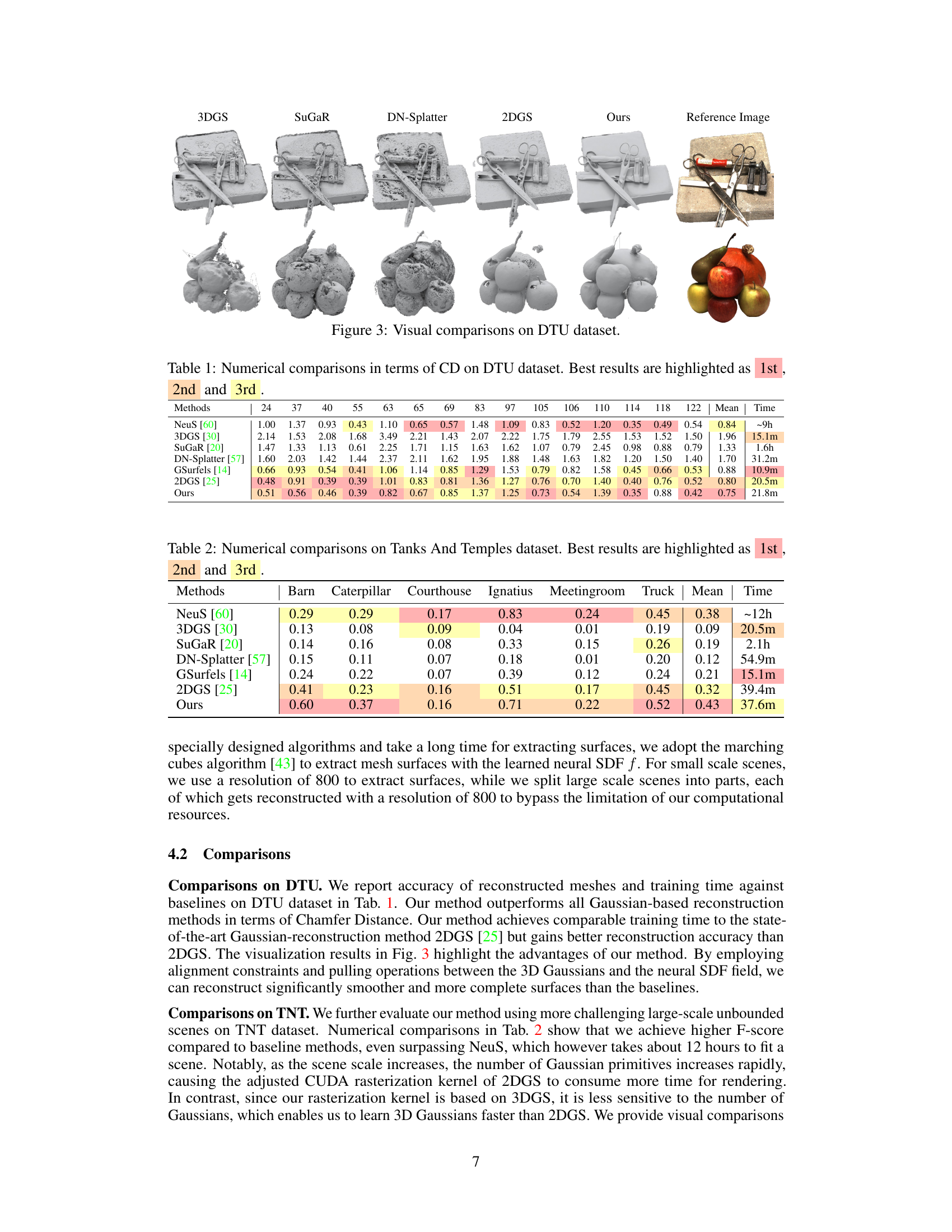
This figure presents a visual comparison of the 3D reconstruction results obtained using different methods on the DTU dataset. The methods compared include 3DGS, SuGaR, DN-Splatter, 2DGS, and the proposed method. Each column shows the reconstructed model for a specific scene using a particular technique. The rightmost column displays the reference image for the same scene. The images provide a qualitative assessment of the surface reconstruction accuracy and completeness achieved by each method, highlighting the strengths and weaknesses of each approach in terms of detail preservation, surface smoothness, and overall reconstruction fidelity.

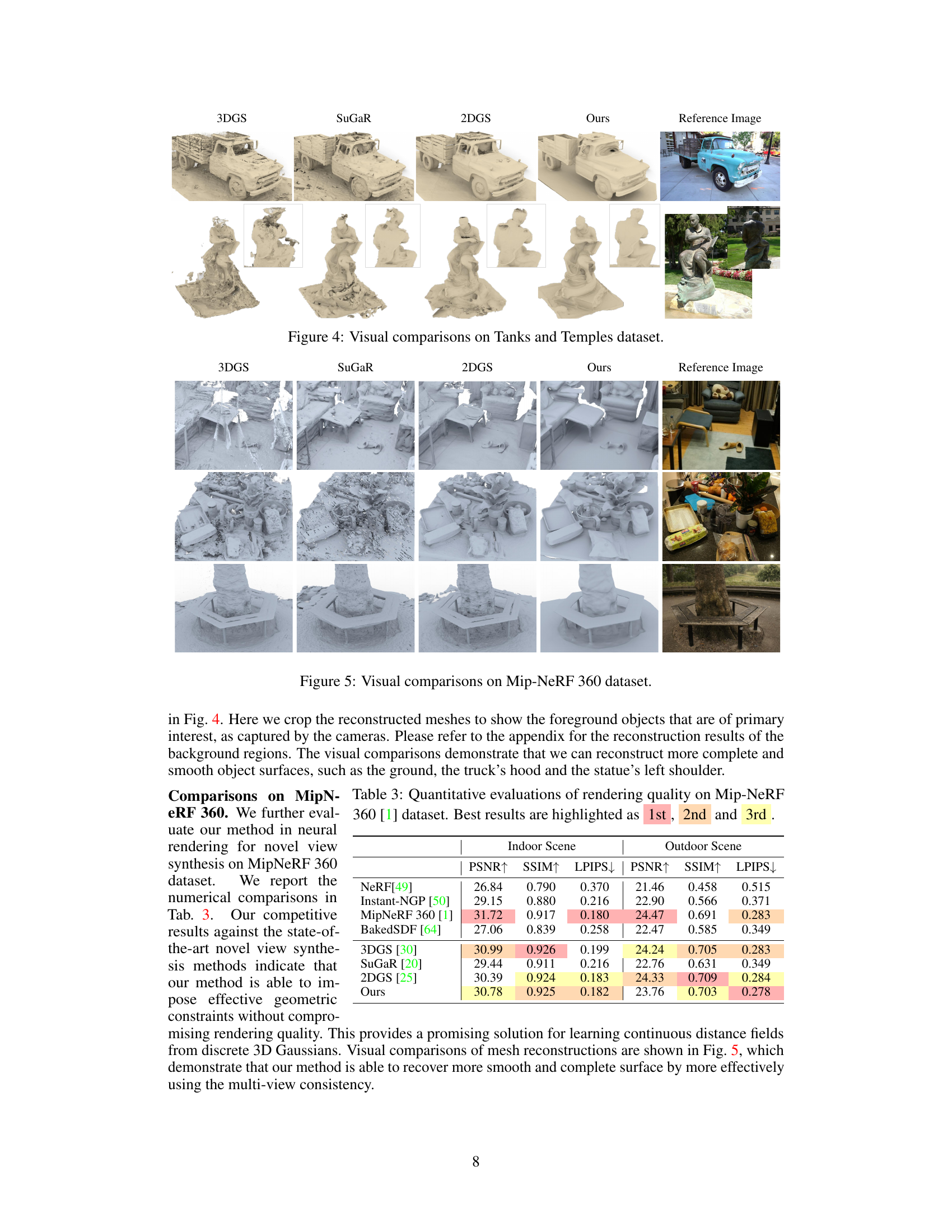
This figure compares the visual results of several methods on the Tanks and Temples dataset. The results show 3D reconstructions of two scenes: a damaged truck and a statue. Each column represents a different method: 3DGS, SuGaR, 2DGS, and the authors’ proposed method. The final column shows the reference image for comparison. The figure highlights the differences in reconstruction quality, particularly in terms of surface smoothness, completeness, and detail.

This figure shows a visual comparison of the results obtained by different methods on the DTU dataset. Each row represents a different scene, with the results from 3DGS, SuGaR, DN-Splatter, 2DGS, and the proposed method shown side-by-side, along with the reference image. The comparison highlights the improvements in surface reconstruction quality achieved by the proposed method, showing smoother, more complete surfaces with finer details compared to the baseline methods.

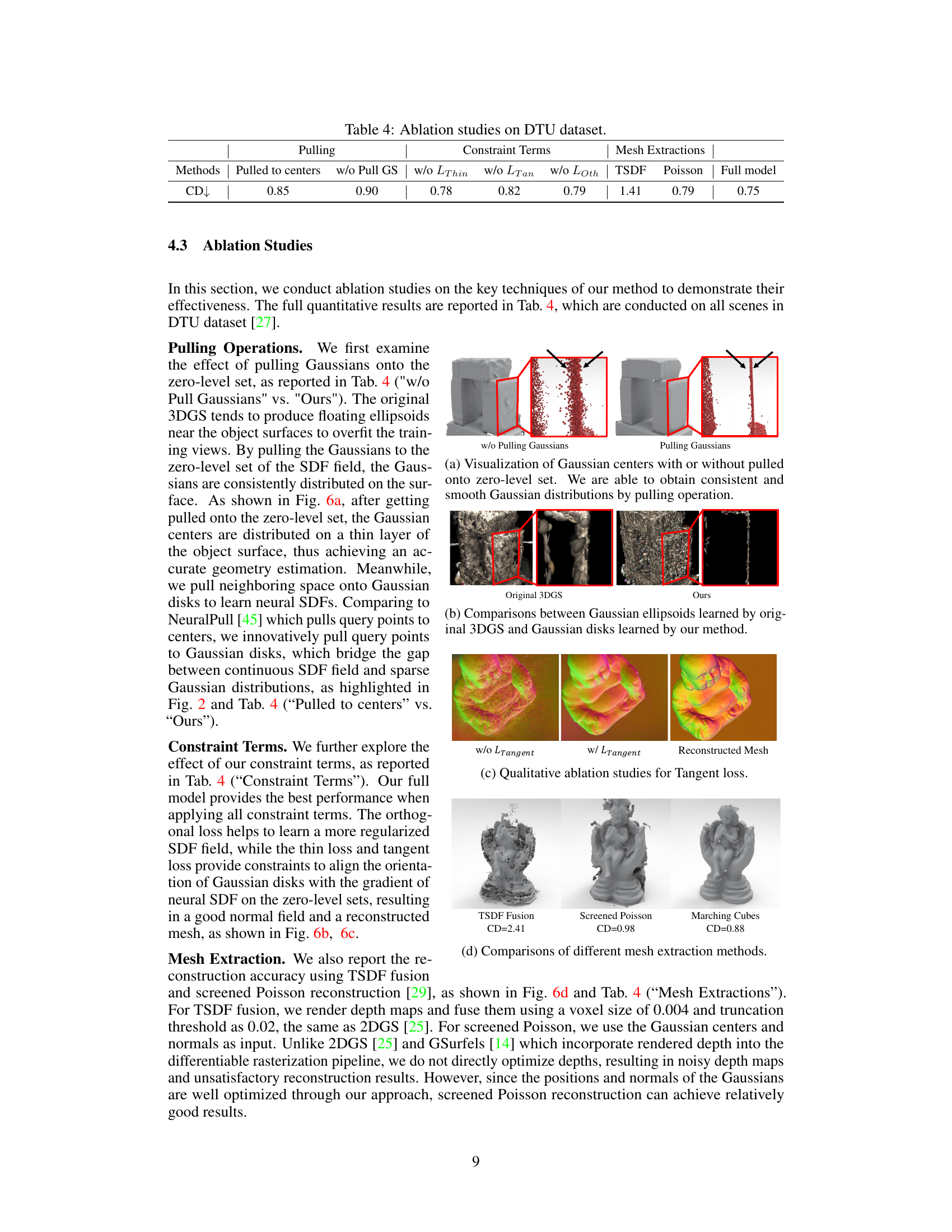
This figure demonstrates the effect of pulling Gaussians to the zero level set in the proposed method. Subfigure (a) shows that pulling Gaussians results in a consistent and smooth distribution, while not pulling them results in a scattered distribution. Subfigure (b) shows a comparison of Gaussian ellipsoids from the original 3DGS and Gaussian disks from the proposed method. Subfigure (c) shows the effect of the Tangent loss, and Subfigure (d) compares different mesh extraction methods.
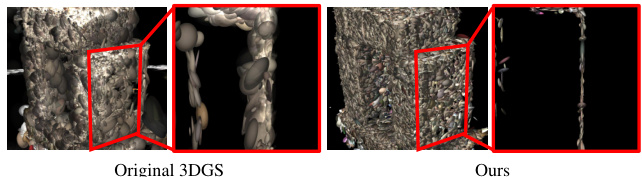
This figure presents a qualitative comparison of the effects of several components of the proposed method. It shows how pulling Gaussians to the zero-level set leads to more consistent Gaussian distributions, and how using Gaussian disks instead of points for pulling improves the quality of the learned neural SDF. The figure also demonstrates the relative effectiveness of different mesh extraction techniques.
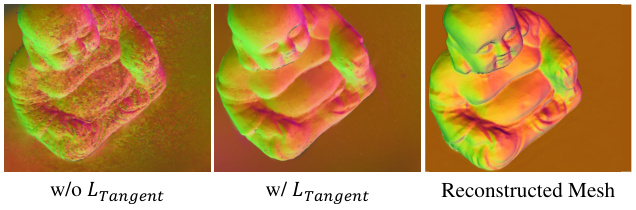
This figure shows the qualitative results of ablation studies on the Tangent loss. The leftmost image shows the result without the Tangent loss, which demonstrates that the surface is not smooth. The middle image shows the result with the Tangent loss, demonstrating a smoother surface. The rightmost image shows the reconstructed mesh, with a very smooth surface and finer details.

This figure illustrates the overall workflow of the proposed method. It shows how 3D Gaussians are pulled onto the zero-level set of a neural SDF for splatting to generate RGB images and how the neighboring space is pulled to refine the SDF. Three constraints are introduced to ensure proper alignment and shape of the Gaussians during the process.
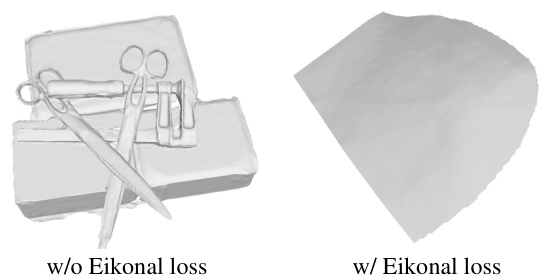
This figure shows a visual comparison of the results with and without the Eikonal loss. The left image shows the result without Eikonal loss, exhibiting less defined and smoother surfaces. The right image, incorporating the Eikonal loss, presents sharper and more detailed surfaces, highlighting the loss’s effectiveness in enhancing surface reconstruction.

The figure presents a visual comparison of 3D model reconstructions generated by different methods on the Tanks and Temples dataset. It showcases the results of 3DGS, SuGaR, 2DGS, and the proposed method (‘Ours’). Each panel displays a 3D reconstruction of the same scene, allowing for a direct visual assessment of the accuracy, completeness, and level of detail achieved by each technique. The differences are particularly evident in the quality of surface reconstruction and the fidelity of small details.
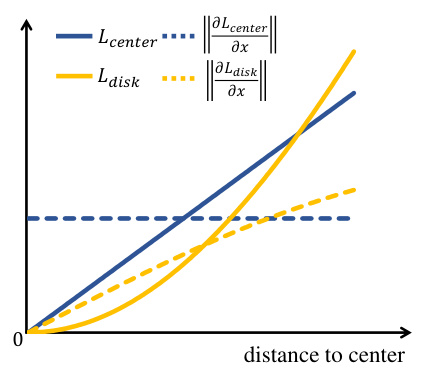
The figure shows a comparison of two loss functions: Lcenter (loss when pulling queries to centers) and Ldisk (loss when pulling queries to disks). The x-axis represents the distance to the Gaussian center. The solid lines represent the loss functions themselves, while the dashed lines represent their gradients (derivatives). Lcenter shows a linear increase in loss and a constant gradient as the distance to the center increases. Ldisk shows a quadratic increase in loss and a decreasing gradient as the distance to the center increases. This illustrates how Ldisk is more tolerant to the query point not being precisely at the center, making it more robust for learning from sparse and non-uniformly distributed Gaussian data.

This figure shows a failure case of the proposed method. The reconstructed mesh of a bulldozer on a patterned surface is smooth and lacks the high-frequency details present in the reference image. This failure is attributed to the limitations of the Multi-Layer Perceptron (MLP) used for the Signed Distance Function (SDF) approximation; MLPs tend to favor smooth, low-frequency features and struggle to capture fine details.

This figure presents a visual comparison of surface reconstruction results on the DTU dataset. It showcases the reconstructed models generated by several different methods, including 3DGS, SuGaR, DN-Splatter, 2DGS, and the proposed method. The reference image for each object is also included for comparison. The purpose is to visually demonstrate the superiority of the proposed method in terms of accuracy, smoothness, and completeness of the reconstructed surfaces.

This figure compares the visual results of different methods (3DGS, SuGaR, 2DGS, and the proposed method) on the Tanks and Temples dataset. The images show the reconstructed 3D models of various scenes, highlighting the differences in surface smoothness, completeness, and detail recovery. The proposed method aims for more accurate, smooth, and complete surface reconstruction with better geometry detail.

This figure provides a visual overview of the proposed method for neural signed distance function (SDF) inference using 3D Gaussian splatting. It shows how 3D Gaussians are pulled onto the zero-level set of the neural SDF (a), and how neighboring space is pulled onto Gaussian disks for SDF inference (b). Three constraints are introduced to improve the accuracy and smoothness of the resulting surface: (c) enforcing thin Gaussian disks, (d) aligning the disk tangent plane with the zero-level set, and (e) pulling query points along the shortest path to the disk.

This figure compares the error maps generated by the 2DGS method and the proposed method on the Tanks and Temples (TNT) dataset. The error maps visualize the difference between the reconstructed surfaces and the ground truth surfaces. Red indicates large errors, while yellow and white represent smaller errors. The comparison aims to show that the proposed method achieves higher accuracy in surface reconstruction compared to 2DGS.

This figure compares the results of reconstructing surfaces using both signed distance functions (SDFs) and unsigned distance functions (UDFs). The left image shows a surface reconstructed using SDF, which is smoother and more complete. The right image shows a surface reconstructed using UDF, which has artifacts and outliers. The difference highlights the challenges of using UDFs for surface reconstruction.
More on tables
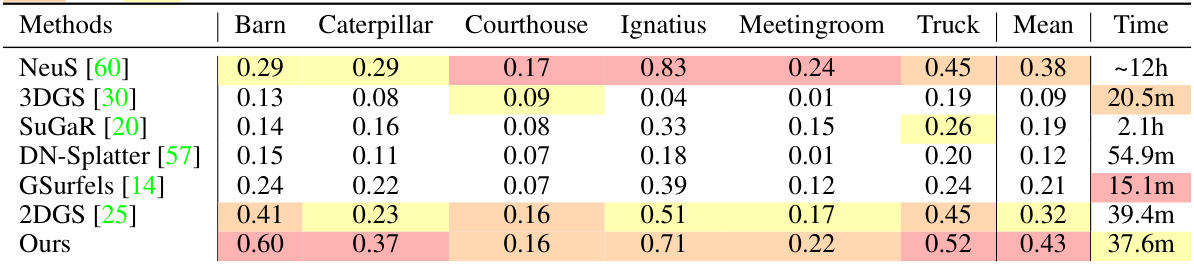
This table presents a quantitative comparison of different methods for 3D reconstruction on the Tanks and Temples dataset. The metrics used are the average F-score across various scenes in the dataset. Lower values indicate better performance. The table also lists the training time for each method. The methods compared include several state-of-the-art techniques using 3D Gaussian splatting as well as a more traditional neural radiance field approach (NeuS). The ‘Ours’ row represents the performance of the proposed method.
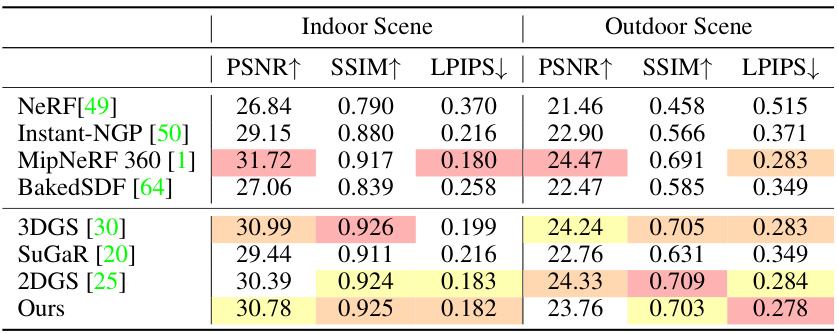
This table presents a quantitative comparison of the rendering quality achieved by different methods on the Mip-NeRF 360 dataset. The metrics used are PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index), and LPIPS (Learned Perceptual Image Patch Similarity). Higher PSNR and SSIM values indicate better rendering quality, while a lower LPIPS value indicates better perceptual similarity to the ground truth images. The table shows the results for both indoor and outdoor scenes, allowing for a comprehensive comparison of the methods’ performance across different environments and scene complexities.

This table presents the ablation study results on the DTU dataset, evaluating the impact of different components of the proposed method on the Chamfer Distance (CD) metric. The columns represent different configurations: pulling Gaussian primitives to centers vs. the zero level set; excluding specific loss terms (thin, tangent, orthogonal); and using different surface extraction methods (TSDF fusion, Poisson reconstruction). The full model represents the complete method.
Full paper#