GSDF: 3DGS Meets SDF for Improved Neural Rendering and Reconstruction

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents a novel solution to a long-standing problem in 3D scene representation: the trade-off between high-fidelity rendering and accurate geometric reconstruction. GSDF’s dual-branch architecture and mutual guidance strategy offers a significant advancement, paving the way for more realistic and accurate virtual and augmented reality applications. The method’s versatility and adaptability also open doors for future research in hybrid representation methods.

Visual Insights

#

This figure illustrates the core idea of the GSDF method. It compares three approaches to 3D scene representation: 3DGS, a method using explicit regularization, and the proposed GSDF method. 3DGS excels at rendering but lacks geometric accuracy. Explicit regularization improves geometric accuracy but compromises rendering quality. GSDF, a dual-branch network combining 3DGS and SDF, aims to address these trade-offs by using three mutual guidances to improve both rendering and reconstruction. The figure uses a diagram of Gaussian primitives to show how each method represents a simple circular scene and highlights the strengths and weaknesses of each approach.

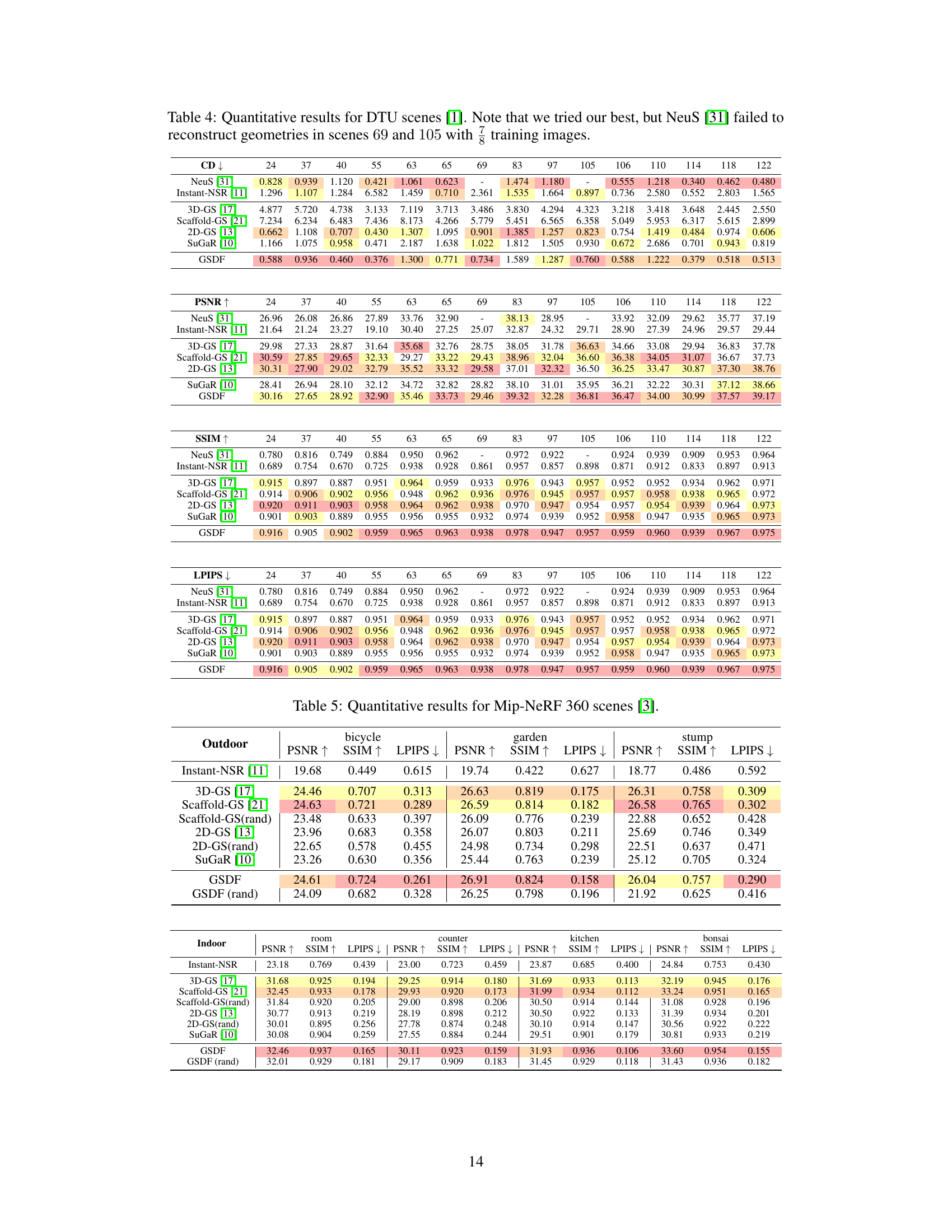
This table presents a quantitative comparison of rendering and reconstruction performance between GSDF and several baseline methods across four benchmark datasets. The metrics used include PSNR, SSIM, LPIPS for rendering quality and Chamfer Distance for reconstruction accuracy. It highlights GSDF’s superiority in both rendering and reconstruction tasks compared to other methods, especially in terms of perceptual quality (LPIPS). Note that all compared models were initialized using sparse points from COLMAP.

In-depth insights

#

GSDF: Dual-Branch Fusion

#

The proposed GSDF framework leverages a dual-branch architecture to overcome the limitations of traditional neural scene representation methods. One branch utilizes 3D Gaussian Splatting (3DGS) for high-fidelity rendering, while the other employs neural Signed Distance Fields (SDF) for accurate geometric reconstruction. Mutual guidance between these branches is crucial; the 3DGS branch provides depth information to guide efficient ray sampling in the SDF branch, improving reconstruction accuracy. Conversely, SDF’s surface information refines the density and placement of Gaussian primitives in the 3DGS branch, leading to improved rendering quality. This sophisticated fusion resolves the traditional trade-off between rendering and reconstruction, ultimately achieving enhanced visual fidelity and geometric precision. The core innovation lies in simultaneously optimizing both branches via mutual guidance and joint supervision, rather than sequentially optimizing them, leading to superior overall results.

Mutual Guidance

#

The core concept of “Mutual Guidance” in this research lies in the synergistic interplay between two neural network branches: one focused on rendering using 3D Gaussian Splatting (3DGS) and the other on surface reconstruction via Signed Distance Fields (SDFs). This dual-branch approach cleverly addresses the inherent trade-off between rendering quality and geometric accuracy often encountered in single-representation methods. The “guidance” is bidirectional, meaning each branch refines the other’s output. The 3DGS branch provides depth maps to guide efficient ray sampling within the SDF branch, enhancing reconstruction. Conversely, the SDF branch’s surface estimates inform the density and distribution of Gaussian primitives in the 3DGS branch, improving rendering detail and reducing artifacts. This iterative refinement process, facilitated by joint supervision during training, leads to superior results in both rendering and reconstruction tasks. This mutual learning mechanism is key to achieving high-fidelity visuals with accurate underlying geometry, a significant advancement over existing methods that prioritize one task over the other.

Geometry-Aware Density

#

The concept of “Geometry-Aware Density” in neural scene representation addresses the challenge of balancing rendering quality and geometric accuracy. Traditional methods often prioritize one over the other. Geometry-aware density dynamically adjusts the density of primitives (e.g., Gaussian splatters or implicit surface points) based on proximity to the underlying 3D geometry. This is crucial because high density near surfaces enhances fine detail in rendering, while lower density in free space reduces computation and prevents artifacts such as “floaters.” The key is using information from a geometric representation (e.g., SDF) to guide density control in the rendering representation (e.g., 3DGS). This approach avoids explicit regularization that can limit expressiveness, allowing for high-fidelity visuals with accurate geometry. Effective implementation requires robust mechanisms for growing primitives in high-density regions and pruning them in low-density regions. This density modulation is crucial for achieving the desired balance between detailed rendering and efficient computation, making geometry-aware density a significant step towards creating unified and highly effective neural scene representations. The effectiveness of this approach depends on the accuracy of the geometric representation and the sophistication of the density control algorithm. It also creates potential for optimization in training, speeding convergence.

Limitations and Future

#

The research paper’s limitations section should thoroughly address the shortcomings of the proposed GSDF framework. Computational expense, especially during ray-sampling in the SDF branch, is a major limitation, impacting training time significantly. The framework’s current inability to effectively handle scenes with complex lighting, such as reflections and intense illumination, represents another significant limitation. Further exploration of improving the efficiency of the MLP-based SDF branch would be beneficial. Future work should focus on addressing these limitations. Exploring advanced techniques for efficient ray sampling and adapting the framework to manage high-frequency details in challenging scenarios are key avenues for improvement. Addressing the memory consumption and expanding capabilities to handle reflections and complex lighting conditions would significantly enhance the practicality and robustness of the GSDF approach. Investigating the application of more structured Gaussian primitives in scenes with significant view-dependent changes is another worthwhile future research direction. Finally, a comprehensive quantitative analysis of the method’s performance under varying conditions would be valuable.

Ablation Study

#

An ablation study systematically evaluates the contribution of individual components within a complex model. In the context of a neural rendering and reconstruction system like the one described, this would involve removing or deactivating specific modules (e.g., depth-guided ray sampling, geometry-aware density control, mutual geometry supervision) and analyzing the impact on both rendering quality and reconstruction accuracy. The results reveal which components are crucial for achieving high performance, while revealing potential redundancy or detrimental effects. Key insights gained include identifying essential elements contributing most significantly to performance, highlighting the efficacy of individual components. A well-designed ablation study strengthens the overall claims by showcasing not only the model’s capabilities but also its robustness and the importance of each contributing factor. Such analysis provides a deeper understanding of the interplay between different modules and facilitates improvements to future model designs. The comparison between the full model and the ablated versions offers quantifiable evidence supporting the effectiveness of the proposed architecture. By demonstrating improvements from the full model over ablated versions, one can firmly establish the benefits of the design choices made.

More visual insights

#

More on figures

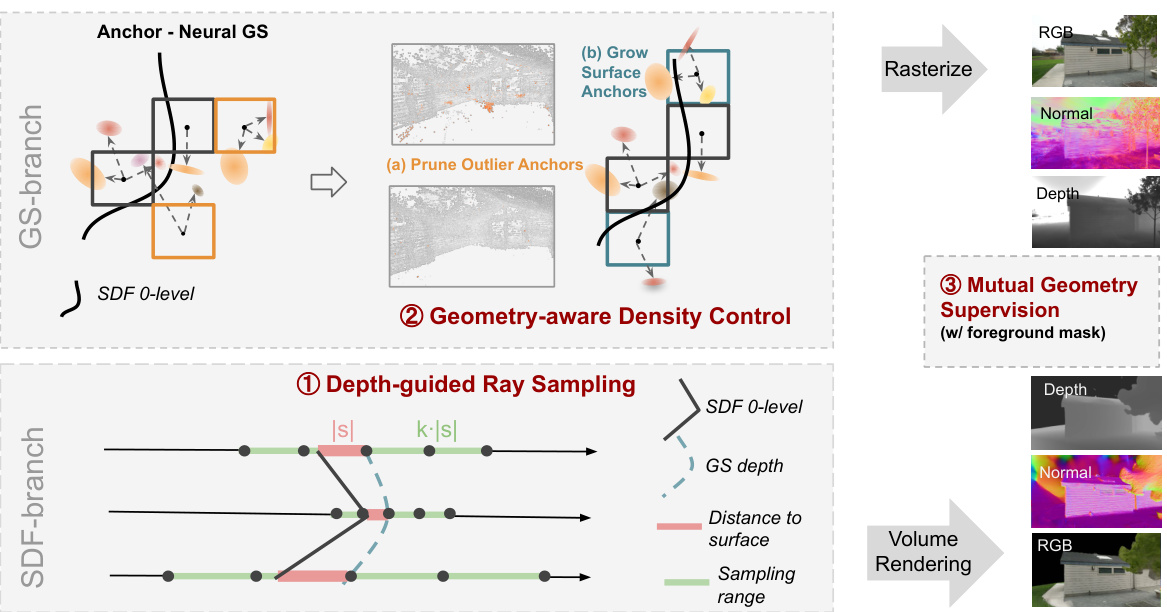
This figure illustrates the dual-branch guidance framework of GSDF. It shows how the GS-branch (for rendering) and the SDF-branch (for surface reconstruction) interact through three mutual guidance mechanisms: depth-guided ray sampling, geometry-aware density control, and mutual geometry supervision. These mechanisms improve the accuracy and efficiency of both rendering and reconstruction.

This figure shows a qualitative comparison of GSDF against three other Gaussian-based neural rendering methods (2D-GS, 3D-GS, and Scaffold-GS) on various scenes. The comparison highlights GSDF’s superior ability to model fine details and handle scenes with less texture or sparse observations, especially in larger scenes where other methods struggle.

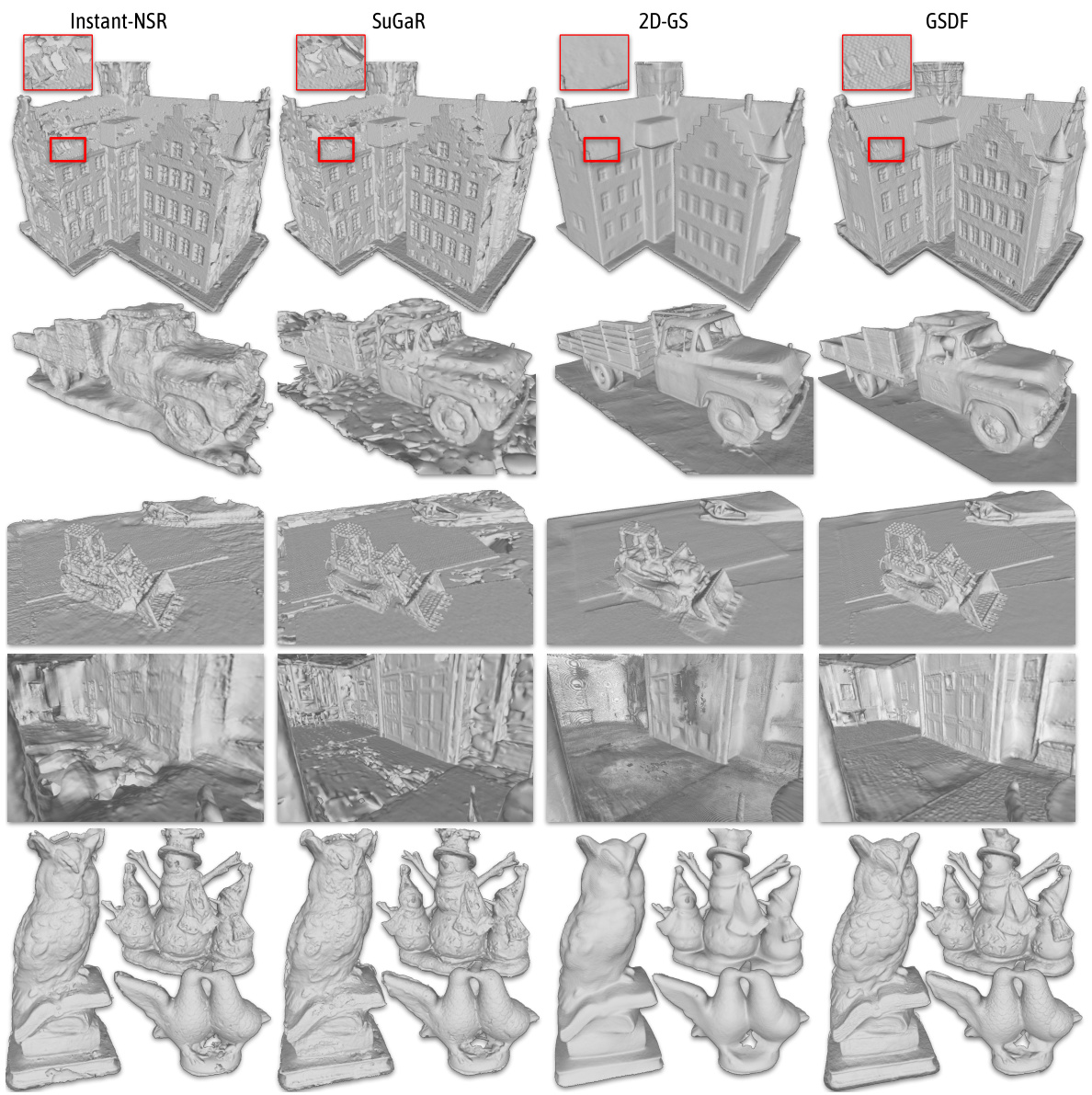
This figure compares the 3D reconstruction results of four different methods: Instant-NSR, SuGaR, 2D-GS, and the authors’ proposed GSDF method. Each row shows the reconstruction of a different scene. The figure visually demonstrates that GSDF produces more complete and detailed meshes compared to the other methods, particularly in capturing fine details and preventing holes or broken surfaces. The differences highlight the effectiveness of GSDF in accurately reconstructing complex 3D shapes.

This figure presents an ablation study to show the effectiveness of each component of the GSDF model. The top row displays the reconstructed surfaces from four different versions of the model: the complete GSDF model and three variations where one component is removed. The bottom row shows rendered images corresponding to each reconstruction. Numbered boxes highlight specific areas where the removal of a component leads to noticeable degradation in reconstruction or rendering quality. The components tested are depth-guided ray sampling, geometry-aware density control, and mutual geometric supervision.

This figure compares the 3D reconstruction results of four different methods: Instant-NSR, SuGaR, 2D-GS, and the authors’ proposed GSDF method. The results are shown for three different scenes, visualizing the meshes generated by each method for each scene. The comparison highlights the GSDF method’s ability to reconstruct more accurate and detailed meshes compared to the other methods.

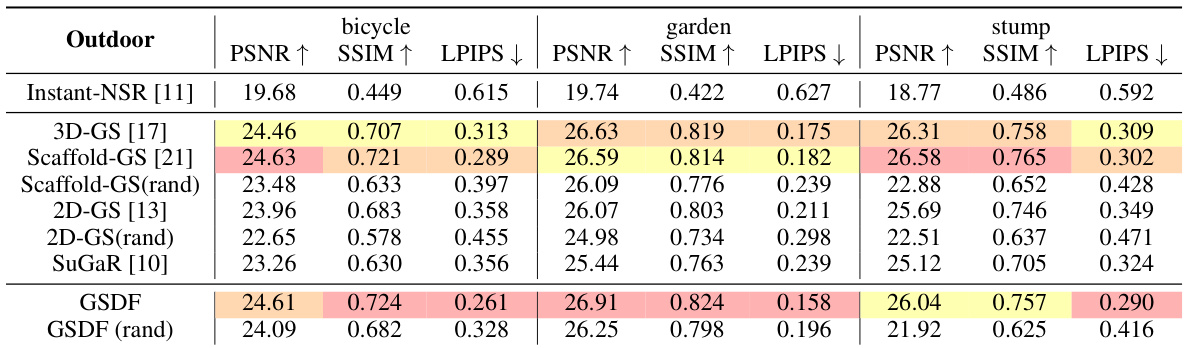
This figure compares the rendering results of three methods: GT (ground truth), Scaffold-GS (with random initialization), and GSDF (with random initialization). The comparison highlights GSDF’s superior performance in capturing fine details in both geometry and appearance. Specific areas are highlighted using colored boxes to show improvements in detail and accuracy. This demonstrates the effectiveness of the GSDF approach compared to a baseline Gaussian Splatting method.

This figure shows a comparison of rendering results between Scaffold-GS and the proposed GSDF method, both using randomly initialized Gaussian primitives. The comparison highlights the superior ability of GSDF in capturing finer details in both geometry and appearance, as evidenced by the highlighted regions showing improved detail and accuracy in GSDF’s renderings.

More on tables

This table compares the rendering performance (PSNR, SSIM, LPIPS) of three methods: Scaffold-GS, 2D-GS, and GSDF. Each method uses randomly initialized Gaussian primitives, and results are shown for three benchmark datasets (Mip-NeRF360, Tanks&Temples, Deep Blending). The table demonstrates GSDF’s robustness and superior performance even with random initialization.

This table presents the results of ablation studies conducted to evaluate the effectiveness of each individual module in the GSDF model. It shows the rendering metrics (PSNR, SSIM, LPIPS) for the full GSDF model and for variations where components like geometric supervision, depth-guided sampling, and geometry-aware densification are removed. This allows for a quantitative assessment of the contribution of each module to the overall performance.

This table presents a quantitative comparison of the proposed GSDF method against several state-of-the-art baselines for both rendering and reconstruction tasks. The comparison is made across four benchmark datasets, using metrics like PSNR, SSIM, LPIPS (for rendering), and Chamfer Distance (for reconstruction). Importantly, it notes that all methods (including GSDF) used sparse points from COLMAP for initializing Gaussian primitives.

This table presents a quantitative comparison of the proposed GSDF method against several state-of-the-art baselines for both rendering and reconstruction tasks. The comparison is performed across four benchmark datasets using metrics like PSNR, SSIM, LPIPS (for rendering), and Chamfer Distance (for reconstruction). All methods used sparse points from COLMAP for initialization of Gaussian primitives. The table highlights GSDF’s superior performance in both rendering quality and reconstruction accuracy compared to the baselines.

This table presents a quantitative comparison of rendering and reconstruction performance between GSDF and several baselines (3D-GS, Scaffold-GS, 2D-GS, and SuGaR) across four benchmark datasets. The metrics used include PSNR, SSIM, LPIPS (for rendering), and Chamfer Distance (for reconstruction). All methods used COLMAP sparse points to initialize Gaussian primitives.

This table presents a quantitative comparison of rendering and reconstruction performance between GSDF and several baseline methods (3D-GS, Scaffold-GS, 2D-GS, and SuGaR) across four benchmark scenes. The metrics used include PSNR, SSIM, LPIPS (for rendering), and Chamfer distance (for reconstruction). All methods used COLMAP sparse points to initialize Gaussian primitives.

This table presents a quantitative comparison of rendering and reconstruction performance between the proposed GSDF method and several baselines (3D-GS, Scaffold-GS, 2D-GS, and SuGaR) across four benchmark datasets. The metrics used include PSNR, SSIM, LPIPS (for rendering), and Chamfer distance (for reconstruction). The Gaussian primitives in all methods were initialized using sparse points from COLMAP.

This table presents a quantitative comparison of rendering and reconstruction performance between the proposed GSDF method and several baseline methods (3D-GS, Scaffold-GS, 2D-GS, and SuGaR) across four benchmark scenes. The metrics used for evaluation include PSNR, SSIM, LPIPS (for rendering), and Chamfer Distance (for reconstruction). All methods used COLMAP sparse points for the initialization of Gaussian primitives, ensuring a fair comparison.

This table presents a quantitative comparison of the proposed GSDF method against several state-of-the-art baselines for both rendering and reconstruction tasks across four benchmark datasets. The metrics used for rendering include PSNR, SSIM, and LPIPS, while the reconstruction performance is evaluated using Chamfer Distance (CD). All methods used COLMAP sparse points for Gaussian primitive initialization, ensuring a fair comparison. The table highlights GSDF’s superior performance across all metrics.

Full paper

#