↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Learning complex functions using neural networks is a central problem in machine learning. While significant progress has been made, understanding the optimal sample complexity (the minimum data needed to accurately learn the function) remains a challenge, especially for deep and wide networks. Existing theoretical tools often struggle with the complexity of large neural networks, limiting our ability to provide precise predictions of learning performance. Previous work has demonstrated Bayes-optimal error, but only for the regime of linearly many samples in relation to the input dimension. The challenge of extending this to the more practical and interesting quadratically-many-samples regime remained open.
This paper addresses this open challenge for single hidden layer neural networks with quadratic activation functions, deriving a closed-form expression for the Bayes-optimal test error. It also introduces a novel algorithm, GAMP-RIE, combining approximate message passing (AMP) with rotationally invariant matrix denoising (RIE) and shows that it asymptotically achieves this optimal error. The results are enabled by a connection to recent advances in extensive-rank matrix denoising, linking seemingly disparate fields and opening up new avenues of research.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on high-dimensional learning, neural network theory, and Bayesian inference. It provides new theoretical tools and algorithmic approaches to understand the fundamental limitations and optimal performance in learning complex neural networks, impacting various fields that leverage these techniques.
Visual Insights#
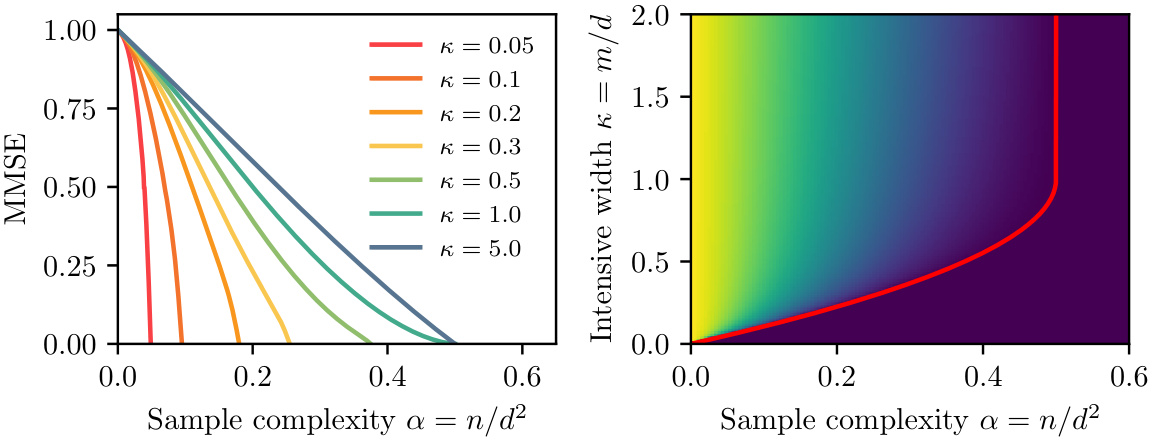
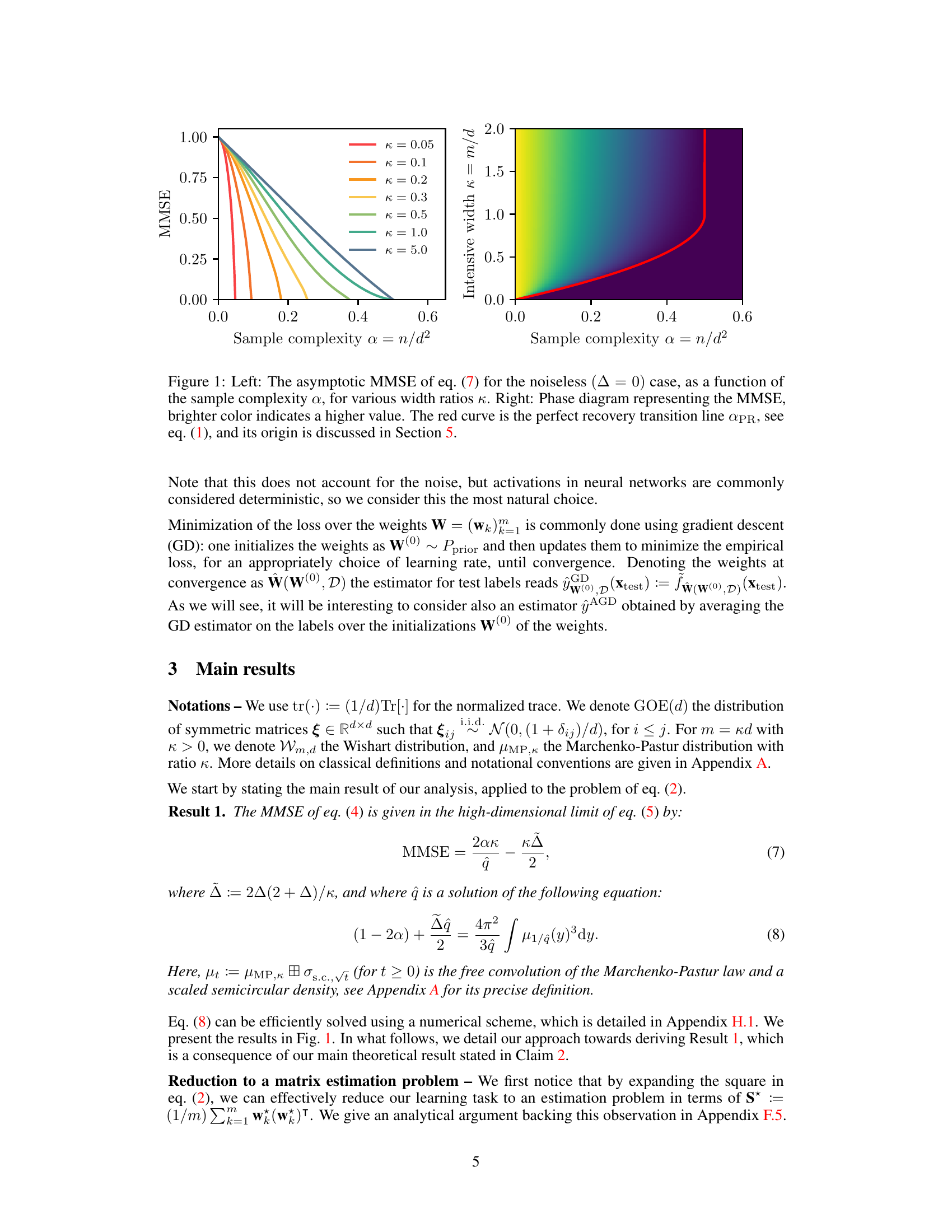
The figure shows two plots related to the minimum mean-squared error (MMSE) in learning a single hidden layer neural network with quadratic activation function. The left plot shows the MMSE as a function of sample complexity (α = n/d²) for different width ratios (κ = m/d). The right plot is a phase diagram showing the MMSE as a function of both sample complexity and width ratio. The red curve in the right plot represents the perfect recovery transition line (APR), which indicates the minimum sample complexity needed to achieve zero test error in the absence of noise.
In-depth insights#
Bayes-Optimal Error#
The concept of “Bayes-Optimal Error” in the context of this research paper centers on determining the fundamental limits of learning a target function represented by a neural network. It specifically addresses the minimum achievable test error when the true underlying function is unknown and only statistical properties about its generation are available. This is a significant departure from typical machine learning analyses that often focus on algorithm-specific performance. The paper highlights the Bayes-optimal error as a benchmark, providing a theoretical lower bound against which any learning algorithm’s performance can be measured. Finding a closed-form expression for this error, especially for neural networks with extensive width and quadratic activation functions, is a challenging problem that represents a key contribution of this work. The theoretical findings are validated empirically by comparing them to the performance achieved by gradient descent methods. This comparison allows investigation of how well gradient descent explores the landscape of possible network weights, shedding light on its efficiency in achieving near-Bayes optimal performance under various conditions, including the presence of noise.
GAMP-RIE Algorithm#
The GAMP-RIE algorithm is a crucial contribution of the paper, combining the strengths of Generalized Approximate Message Passing (GAMP) and Rotationally Invariant Estimators (RIE). GAMP’s iterative nature efficiently handles high-dimensional data, while RIE excels at denoising extensive-rank matrices, a critical step in learning neural networks. The algorithm’s design directly targets the Bayes-optimal test error for learning neural networks with quadratic activations, demonstrating its theoretical foundation and practical effectiveness. The integration of RIE is particularly innovative, enabling the algorithm to achieve optimal performance even with quadratically many samples, a regime that poses significant challenges for simpler methods. Empirical results strongly support GAMP-RIE’s ability to reach the Bayes-optimal error, showcasing its potential as a powerful tool for learning complex neural network models.
Quadratic Activations#
The research paper explores the use of quadratic activation functions in neural networks, particularly focusing on the Bayes-optimal learning setting. This choice of activation function presents several interesting properties. Firstly, it allows for a closed-form expression for the Bayes-optimal test error, a significant theoretical achievement which is often intractable with other activation functions. This closed-form solution facilitates a deeper understanding of the fundamental limits of learning in high-dimensional settings. Secondly, the quadratic activation enables a connection with existing theoretical work on the denoising of extensive-rank matrices, thereby providing a powerful analytical tool for studying the optimal learning performance. This linkage simplifies analysis significantly, enabling a more complete theoretical picture. However, the quadratic activation is a specific choice, and it’s essential to remember that generalization to more realistic activation functions, such as ReLU, remains an open and highly challenging task. The paper’s analytical results also suggest that gradient descent may surprisingly achieve near-optimal performance, even in high-dimensional scenarios, raising intriguing questions about the interplay between optimization algorithms and the space of model weights.
High-Dimensional Limit#
The high-dimensional limit is a crucial concept in the paper, analyzing the behavior of neural networks as the input dimension (d) and the number of neurons (m) grow proportionally large. This asymptotic regime simplifies the analysis by allowing the use of tools from random matrix theory and statistical physics. The paper leverages this to derive closed-form expressions for Bayes-optimal test error and sample complexity, which are fundamental limits for learning such networks. It allows a focus on general properties instead of detailed features, providing valuable insights into how the network architecture influences learning capabilities, and it also enables a mathematical link with the extensive-rank matrix denoising and ellipsoid fitting problems, further strengthening the theoretical analysis.
Future Research#
The paper concludes by highlighting several promising avenues for future research. Extending the theoretical framework to handle more general activation functions beyond the quadratic case is a key challenge. This requires addressing the complex mathematical aspects of free probability theory and high-dimensional statistics. Investigating the behavior of gradient descent in this context is another important direction. While empirical observations suggest that gradient descent may sample the weight space effectively, even in non-convex landscapes, a rigorous theoretical understanding is lacking. Exploring the impact of noise on the Bayes-optimal error and comparing it with the performance of gradient descent is also crucial. The paper suggests that with noise, the transition to zero error might be smoother, but further analytical investigation is needed. Finally, generalizing the results to deeper neural networks with multiple hidden layers presents a significant challenge, requiring substantial advances in our understanding of high-dimensional learning theory and the dynamics of gradient-based optimization.
More visual insights#
More on figures
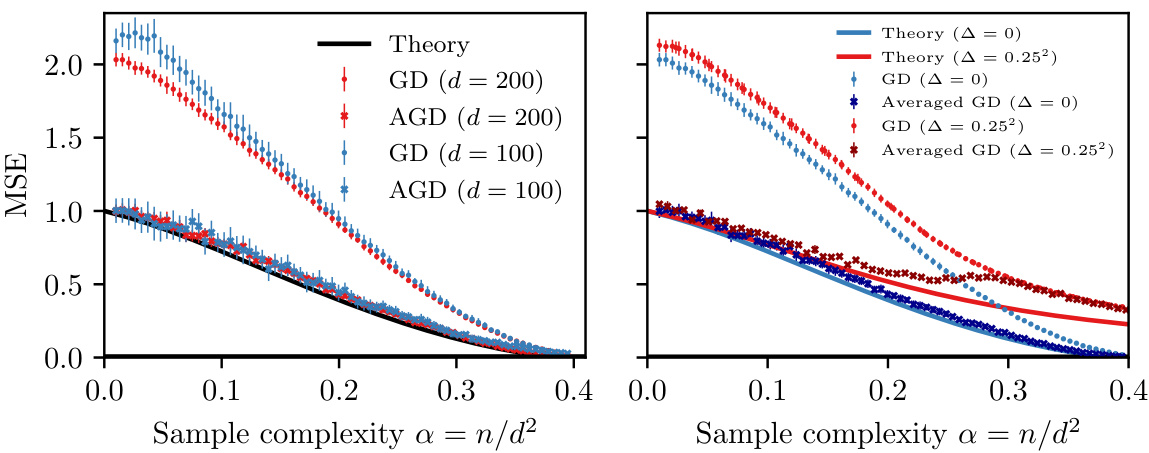
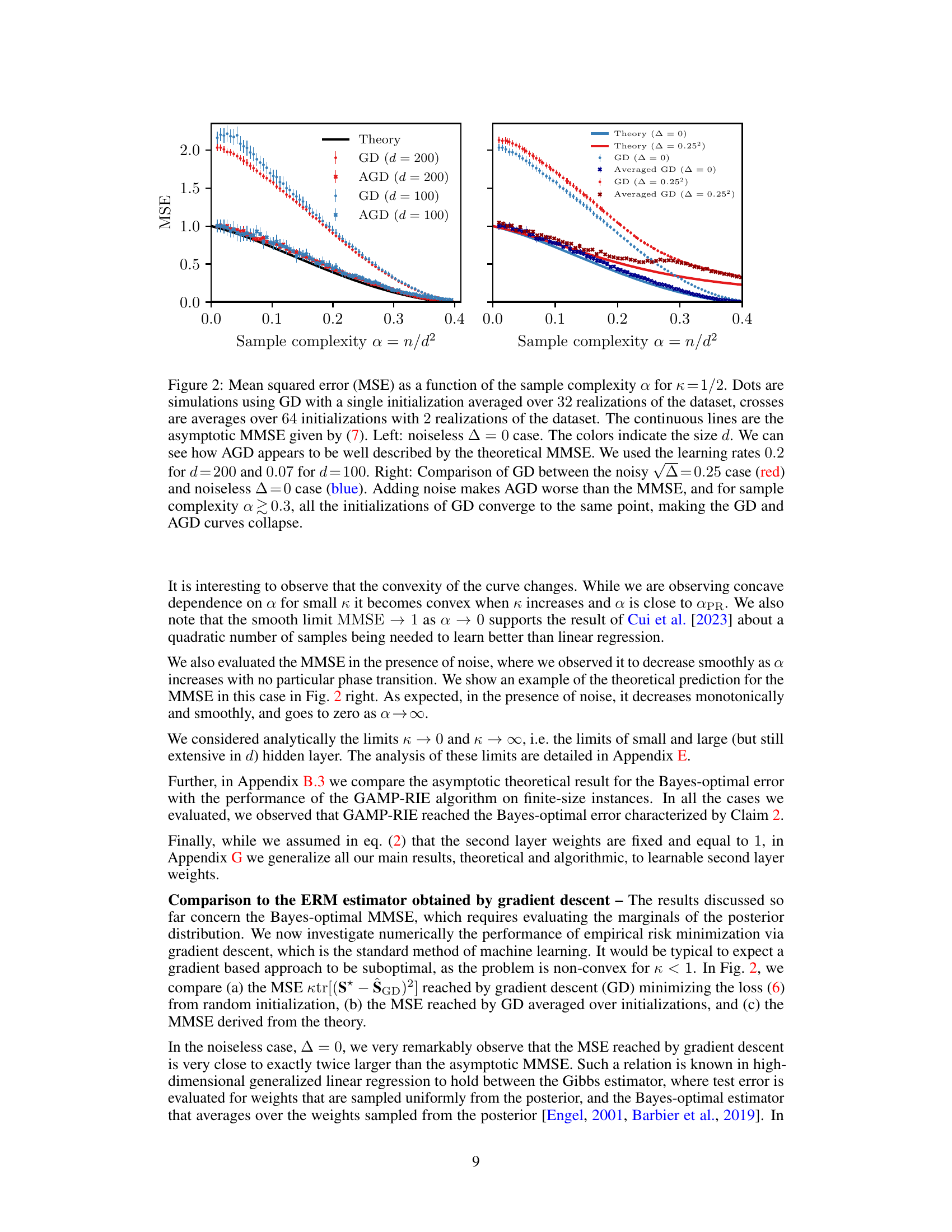
The figure compares the mean squared error (MSE) achieved by gradient descent (GD) and averaged gradient descent (AGD) with the theoretical minimum mean squared error (MMSE) for different sample complexities and dimensions. The left panel shows the noiseless case, demonstrating that AGD closely matches the theoretical MMSE. The right panel introduces noise, showing that AGD performs worse than the MMSE and that GD converges to a single point for larger sample complexities regardless of initialization.
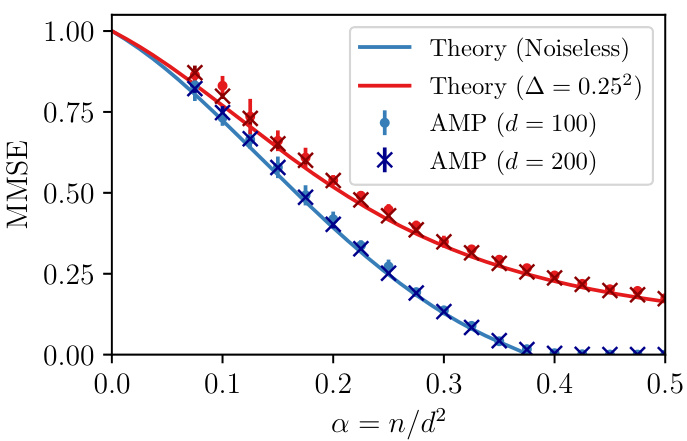
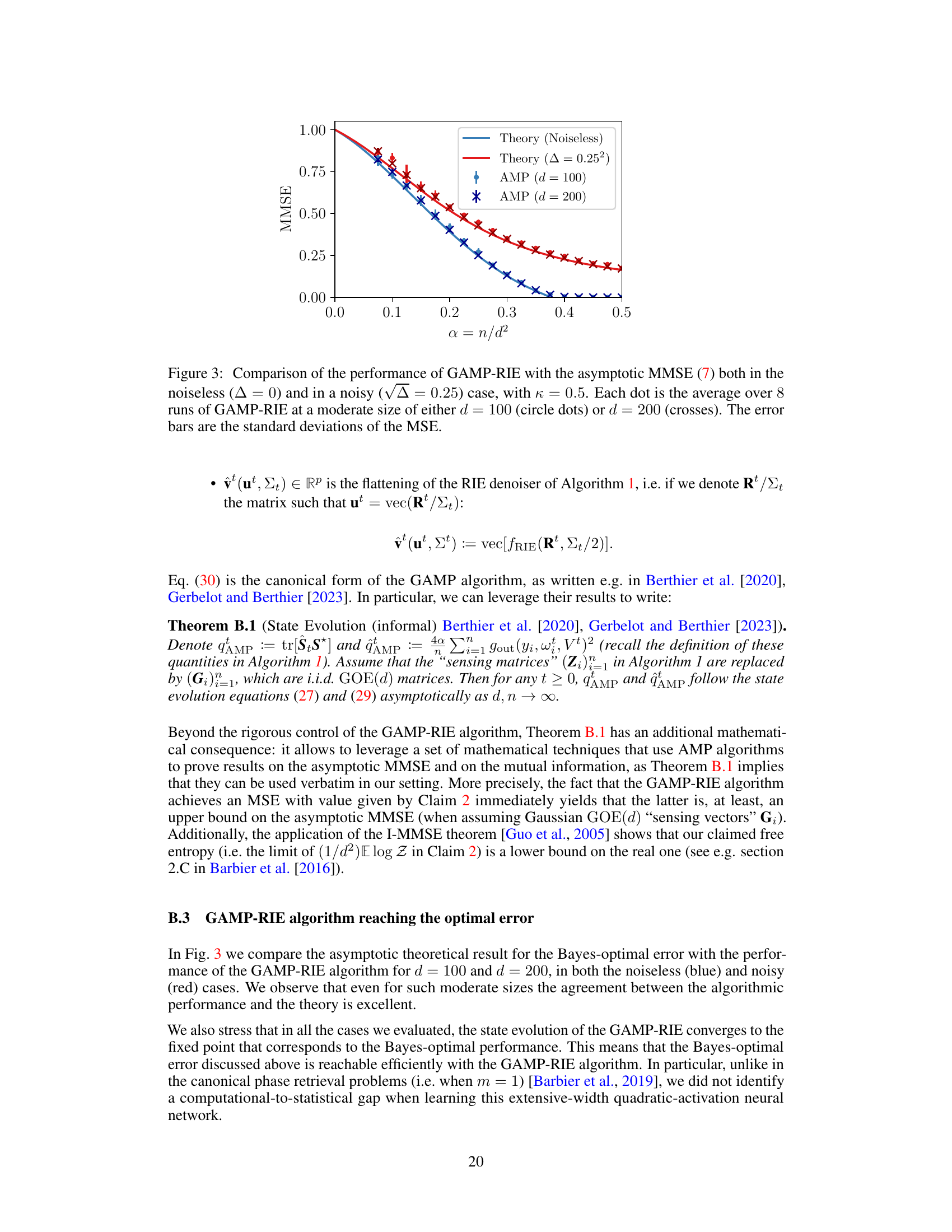
This figure compares the performance of the GAMP-RIE algorithm with the theoretical asymptotic minimum mean-squared error (MMSE) for learning a one-hidden layer neural network with quadratic activation. The comparison is shown for both noiseless and noisy scenarios (noise level √∆ = 0.25), with a width-to-dimension ratio κ = 0.5. The results show a good agreement between the algorithm’s performance and the theoretical MMSE, even for moderately sized networks (d = 100 and d = 200). Error bars represent the standard deviation of the MSE.
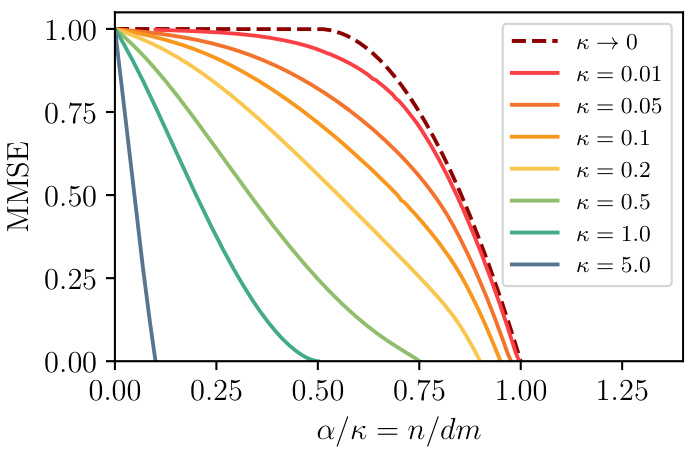
This figure shows the asymptotic minimum mean squared error (MMSE) for different width ratios (κ) in the noiseless case (no noise in target function). The x-axis represents the sample complexity (α/κ) which remains of order 1 as κ goes to 0. The curves show that MMSE decreases smoothly as sample complexity α/κ increases and reaches 0 at perfect recovery. The plot also includes the asymptotic MMSE as κ approaches 0, obtained via an analytical expression.
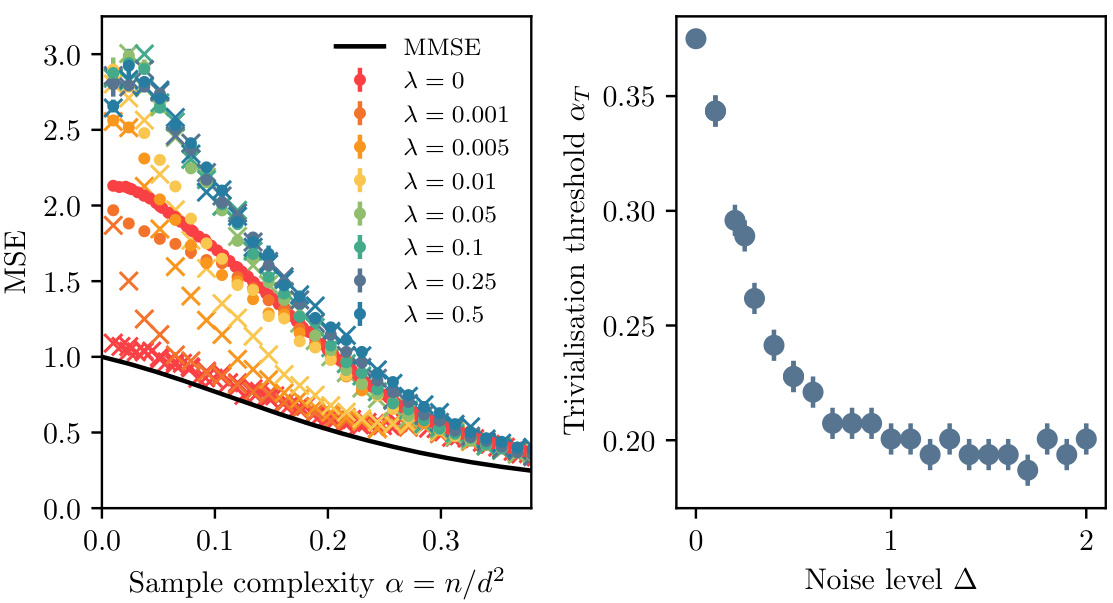
The left panel shows the mean squared error (MSE) as a function of sample complexity (α) for different regularization strengths (λ). The black line represents the theoretical minimum mean squared error (MMSE). The right panel shows the trivialization threshold (ατ) as a function of noise level (Δ) in the teacher network, where trivialization means that gradient descent converges to the same solution regardless of the initialization.
Full paper#