↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Diffusion models generate high-quality images but are computationally expensive due to their iterative sampling process. Existing distillation methods for making faster diffusion models either degrade performance with few sampling steps or fail to capture the full data distribution. This is because most methods use mode-seeking optimization that focuses only on the most likely data points.
EM Distillation (EMD) addresses these issues by using a maximum likelihood-based approach derived from the Expectation-Maximization (EM) algorithm. It leverages a reparametrized sampling scheme and a noise cancellation technique to stabilize the training process, and it effectively minimizes mode-seeking KL divergence, outperforming other single-step generative methods on ImageNet. The results demonstrate the effectiveness of EMD in producing high-quality images with minimal computational cost.
Key Takeaways#
Why does it matter?#
This paper is important because it presents EM Distillation (EMD), a novel method for efficiently training one-step diffusion models. It offers a significant improvement in image generation quality compared to existing methods, particularly for the challenging 1-step generation regime. EMD opens up new avenues for research by combining EM framework and advanced sampling techniques, promising improvements in various other generative models.
Visual Insights#

This figure shows the effect of the MCMC correction on generated images. The left columns show the initial generated images from the student model, while the right columns show the images after 300 steps of MCMC sampling. Subfigure (a) demonstrates the correction on ImageNet images; (b) shows the correction in the Stable Diffusion embedding space; and (c) shows the decoded images from (b) in the image space. The results highlight how MCMC sampling improves image quality and disentangles objects.
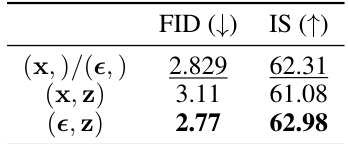
This table presents the results of the EM Distillation (EMD) method with 8 Langevin steps on ImageNet 64x64 after 100,000 training steps. It compares the FID and IS scores achieved using different sampling strategies. (x, z) indicates joint sampling of both x and z, while (ε, z) represents reparametrized sampling using ε and z, and (x, )/(ε, ) uses only one of them. The lower the FID, the better, and the higher the IS, the better, indicating superior image quality and diversity.
In-depth insights#
EM Distillation#
The proposed EM Distillation (EMD) method presents a novel approach to distilling diffusion models into efficient one-step generators. EMD leverages the Expectation-Maximization framework, iteratively refining both generator parameters and latent variables via a maximum likelihood approach. A key innovation is the use of a reparametrized sampling scheme and noise cancellation, which significantly stabilizes the training process and improves sample quality. Unlike methods that rely solely on short-run MCMC or suffer from mode collapse due to mode-seeking KL divergence minimization, EMD’s joint MCMC updates on data and latent pairs ensure a better representation of the entire data distribution, achieving favorable results in image generation benchmarks. The method demonstrates a clear connection to existing techniques like Variational Score Distillation, highlighting a potential path to bridge mode-seeking and mode-covering divergences. Overall, EMD shows a promising approach to bridging the efficiency gap between traditional diffusion models and their faster, simpler alternatives.
MCMC Sampling#
Markov Chain Monte Carlo (MCMC) sampling is a crucial technique within the paper, employed to approximate the intractable posterior distribution of latent variables given observed data. The core idea revolves around constructing a Markov chain whose stationary distribution is the target posterior. The paper leverages MCMC’s ability to generate samples from complex distributions that are otherwise difficult to sample directly. A key innovation is the development of a reparametrized sampling scheme that simplifies hyperparameter tuning and enhances the stability of the distillation process. Furthermore, the authors introduce a noise cancellation technique to mitigate the accumulation of noise during the MCMC iterations, thereby improving the quality of the samples and stabilizing gradient estimation. This demonstrates a thoughtful understanding of the challenges inherent in MCMC and a creative approach to overcome them. The use of MCMC sampling is not simply a standard application; it is integrated into an Expectation-Maximization (EM) framework, highlighting its importance in maximizing likelihood and achieving high-quality results. The method’s effectiveness hinges on the careful design of the MCMC steps, and the paper provides details on the sampling strategy and algorithm, underscoring the importance of the choice for effective convergence and reduced variance in the final results.
Noise Cancellation#
The concept of ‘Noise Cancellation’ in the context of the research paper is crucial for stabilizing the training process and enhancing the quality of the generated samples. The authors identify that the noise accumulation during the Langevin dynamics MCMC process hinders the training. Noise cancellation is presented as a technique to mitigate this issue by systematically removing accumulated noise from samples, significantly reducing variance in the gradients and improving convergence. This is achieved through a careful bookkeeping of the noise introduced at each step of the process and subsequent cancellation. The method’s effectiveness is empirically demonstrated through enhanced model performance and stability, showing a strong correlation between noise cancellation and both FID and Recall. Moreover, the noise cancellation method is shown to be critical for the success of the EMD (Expectation-Maximization Distillation) framework, showcasing its importance in achieving high-quality one-step generation. The authors highlight the technique’s significance in improving the stability and convergence speed of the algorithm while maintaining the accuracy of the learned generative model.
Related Methods#
The section on related methods would likely explore previous work in diffusion model acceleration, focusing on trajectory distillation and distribution matching approaches. Trajectory distillation techniques aim to efficiently sample from diffusion models by simplifying the SDE solving process. However, these methods often struggle with one-step generation. In contrast, distribution matching methods learn implicit generative models that approximate the diffusion model’s distribution, often leading to more efficient sampling but potentially sacrificing the full distribution’s quality due to a tendency towards mode-seeking. The paper would critically analyze these prior methods, highlighting their shortcomings, and positioning its own approach as a novel solution that overcomes those limitations. It would likely emphasize its maximum likelihood-based framework and EM algorithm-inspired approach as key differentiators, providing superior one-step generation performance.
Future Work#
Future research directions stemming from this EM Distillation work could explore several promising avenues. Improving the initialization of the student model is crucial; current reliance on teacher model weights limits the exploration of diverse architectures and lower-dimensional latent spaces. Developing techniques for training from scratch, perhaps incorporating novel regularization strategies or advanced optimization methods, would significantly expand applicability. Addressing the computational cost of multi-step MCMC sampling, while maintaining performance gains, is another key area. Investigating alternative sampling methods or more efficient approximations of the expectation step in the EM framework could reduce training time without sacrificing quality. Finally, a deeper investigation into the connection between EM Distillation and existing methods like Variational Score Distillation is warranted. Understanding how the sampling schemes influence the convergence to mode-covering versus mode-seeking behavior, and exploring strategies to leverage the strengths of both paradigms, could lead to even more powerful generative models. This deeper theoretical understanding could also inform the development of new divergence measures better suited for diffusion model distillation.
More visual insights#
More on figures

This figure shows the effect of the MCMC correction process on image generation. The left side shows images generated before correction (x = gθ(z)), while the right side depicts the same images after 300 steps of MCMC sampling, which corrects off-manifold artifacts and improves image quality. The comparison highlights the correction process on ImageNet and in the Stable Diffusion embedding space. The improved clarity and disentanglement of objects (like cats and a sofa) in the corrected images are clearly visible.
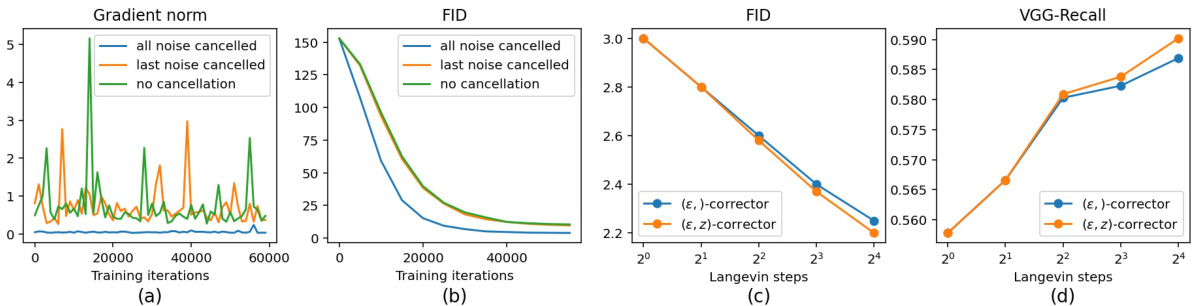
This figure shows the effects of noise cancellation and the number of Langevin steps on the performance of the EM distillation method. (a) compares the gradient norms during training with different noise cancellation strategies. (b) shows the FID scores for the same strategies. (c) and (d) show the FID and Recall scores, respectively, as a function of the number of Langevin steps used.

This figure shows samples generated by the one-step generator model trained on the ImageNet dataset. The model is trained in a class-conditional manner, meaning it is trained to generate images belonging to specific classes. The figure displays multiple generated images for different classes (multi-class) and showcases examples from single classes to demonstrate that the model can capture a variety of modes (different features and styles within a class) and avoid mode collapse (where the model only produces a limited range of similar outputs).

This figure shows samples generated by a one-step generator trained using the proposed EM distillation method. The model was trained on the ImageNet dataset, conditioned on different classes. The images demonstrate the model’s ability to generate high-quality images that capture diverse characteristics of the object classes. The single-class samples (c) are particularly important to show that the model captures various modes within each class rather than concentrating on just one typical representation.

This figure shows the initial denoiser generation at the 0th training iteration for different values of λ*. When λ* = 0, the generated images are pure Gaussian noise. As λ* decreases to -6 and then -10, the generated images become progressively more structured and less noisy, demonstrating the effect of the hyperparameter λ* on the initial state of the generation process. This hyperparameter is used in the EM Distillation method.

This figure shows samples generated by a one-step generator trained using the proposed EM Distillation method on the ImageNet dataset. The images are organized into three sections: (a) multi-class ImageNet 64x64, (b) multi-class ImageNet 128x128, and (c) single-class ImageNet 128x128. The single-class section (c) specifically demonstrates that the model can generate diverse samples within a single class, showcasing its ability to capture the distribution effectively. The images illustrate the quality and diversity of images generated by the one-step model, highlighting the efficacy of the proposed approach.

This figure shows samples generated by a one-step generator model trained using the EM Distillation method. The model was trained on the ImageNet dataset, with separate sections for multi-class and single-class generation. The single-class section is intended to highlight that the model avoids mode collapse and can generate diverse samples within a single class.

This figure shows additional samples generated by the EMD model on ImageNet 64x64 and ImageNet 128x128 datasets. The samples demonstrate the model’s ability to generate diverse and high-quality images, showcasing its performance in various classes and scenarios. The single-class images (c) highlight the model’s ability to generate good mode coverage, which addresses a common limitation of mode-seeking divergence found in some one-step generation methods. This emphasizes the capability of EMD in capturing the full distribution of the data.

This figure shows the effect of MCMC correction on generated images using EM distillation. The left column displays samples generated before correction (x = gθ(z)), while the right shows results after 300 MCMC steps jointly on data (x) and latent variables (z). Subfigure (a) illustrates ImageNet corrections, highlighting improvements in off-manifold samples. (b) shows the correction in the Stable Diffusion embedding space and (c) the decoded image space, emphasizing the disentanglement of image features and improved sharpness.

This figure shows the effect of the MCMC correction process on image generation. The left columns of (a) and (b) show images generated by the student model before MCMC correction, while the right columns show the images after 300 MCMC steps jointly sampling data and latent variables. (a) demonstrates the correction on ImageNet, showing that the off-manifold images are corrected. (b) shows the correction in the Stable Diffusion v1.5 embedding space, which are decoded to the image space in (c). The disentanglement of objects and improved sharpness highlight the effectiveness of MCMC correction.

This figure shows the effect of the MCMC correction method used in the paper. The left columns display images generated directly by the model (x = gθ(z)). After 300 MCMC steps jointly sampling x and z, the right columns show the improved, corrected images. Subfigure (a) demonstrates the correction on ImageNet, showing how off-manifold images are brought onto the data manifold. Subfigure (b) presents the correction within the embedding space of Stable Diffusion v1.5, and (c) shows the corresponding decoded images. The result highlights improved image quality (e.g. sharpness of sofa) and disentanglement (e.g., improved distinction between cat and sofa).

This figure shows the effect of the MCMC correction process in the paper’s EM Distillation method. The left columns of (a) and (b) display images generated by the student model before MCMC correction, showing artifacts or deviations from the target distribution. After 300 MCMC steps, the images (right columns) show improved quality, demonstrating the correction’s ability to refine the samples and align them more closely with the teacher model’s distribution.

This figure shows samples generated by a one-step generator trained using the proposed EM Distillation method. The model was trained on ImageNet, using a class-conditional approach. The figure displays image samples from multiple classes to illustrate the model’s ability to generate diverse images. A separate set of single-class samples is also shown to demonstrate the model’s ability to capture the distinct modes within each class.

This figure shows samples generated by a one-step generator model trained using the EM Distillation method. The model was trained on the ImageNet dataset. The top row shows multi-class samples, demonstrating the model’s ability to generate diverse images from various classes. The bottom row shows single-class samples from the same model, highlighting its capacity to generate high-quality images consistent within each specific class, emphasizing the quality and mode coverage achieved by the model.

This figure shows samples generated by a one-step generator trained using the EM distillation method on the ImageNet dataset. The top row displays multi-class samples (multiple classes of images from the ImageNet dataset). The bottom row focuses on single-class samples to highlight the model’s ability to generate diverse images within a specific class. This visually demonstrates that the model successfully captures the distribution of the dataset and does not suffer from mode collapse (where it only produces images of a few specific types).

This figure shows the effect of the MCMC correction process in the EM Distillation method. It compares samples before and after 300 steps of MCMC sampling. Subfigure (a) demonstrates the correction of off-manifold images from ImageNet. Subfigure (b) shows the correction in the embedding space of Stable Diffusion v1.5, and subfigure (c) displays the decoded images. The improved disentanglement and sharpness in the corrected images highlight the effectiveness of the method.

This figure shows samples generated by a one-step generator trained using the EM distillation method proposed in the paper. The model was trained on the ImageNet dataset, and the images are organized into three subfigures (a,b,c). (a) shows samples from the multi-class ImageNet 64x64 dataset, (b) shows samples from the multi-class ImageNet 128x128 dataset, and (c) shows samples from the single-class ImageNet 128x128 dataset. The single-class samples are used to demonstrate that the model is able to generate diverse samples that are not simply repetitions of a single mode. The figure provides visual evidence of the strong performance of the proposed EM distillation method for generating high-quality, diverse samples.

This figure shows the effect of MCMC correction on generated images. The left columns display initial samples from the student generator, while the right columns show the improved samples after 300 steps of MCMC sampling, jointly optimizing for both data and latent variables. The improvement is visible across different scenarios, including ImageNet and Stable Diffusion. The correction leads to sharper images and better disentanglement of features.

This figure demonstrates the effect of the MCMC correction process on generated images. The left columns show initial images generated by the student model (x = gθ(z)), while the right columns show the images after 300 MCMC steps which jointly correct the data (x) and latent (z) variables. The top row shows results from the ImageNet dataset, highlighting how the correction pulls off-manifold images back onto the data manifold. The second and third rows depict the correction process within the embedding and image spaces of Stable Diffusion v1.5 respectively, showcasing improvements in detail (e.g., sharpness and disentanglement of objects).

This figure shows samples generated by a one-step generator trained using the EM distillation method on the ImageNet dataset. The models were trained using class-conditional generation, meaning that each model was trained to generate images from a specific class. The figure showcases the quality and diversity of the generated images, with a subfigure (c) specifically highlighting the model’s ability to generate diverse examples within a single class.
More on tables
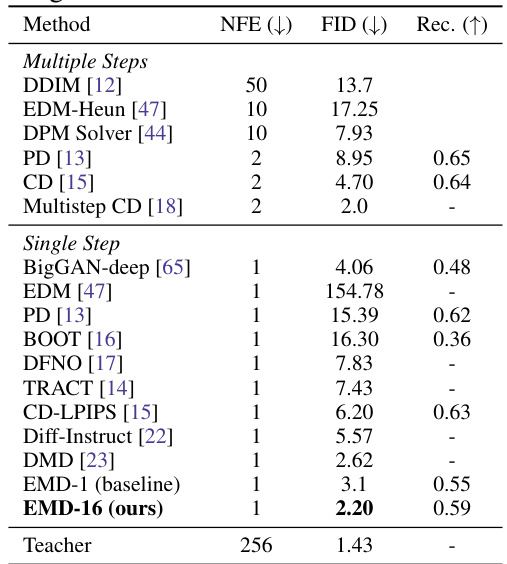
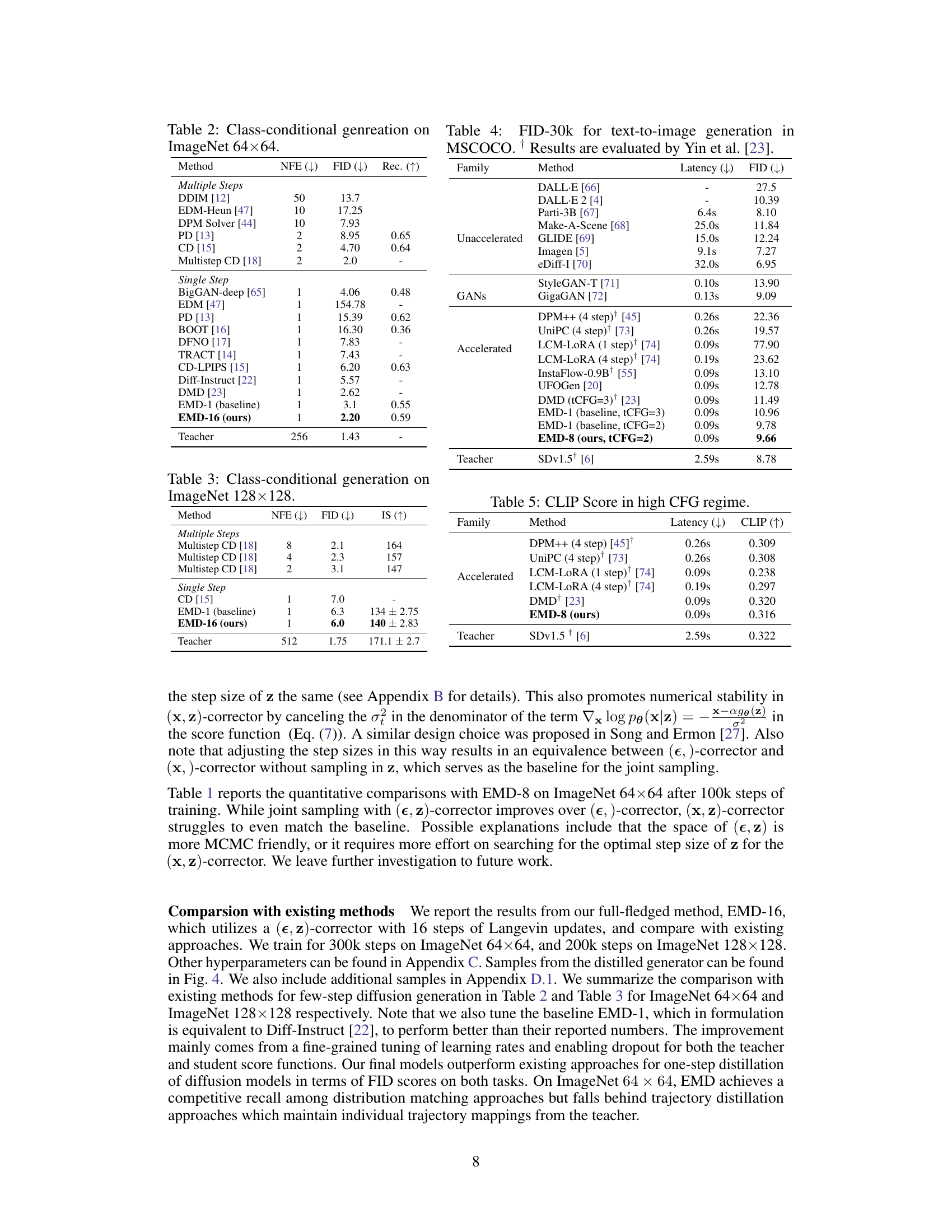
This table presents the results of class-conditional image generation on the ImageNet 64x64 dataset. It compares various methods, both those involving multiple sampling steps and those using a single step. The metrics used for comparison are Number of Function Evaluations (NFE), Frechet Inception Distance (FID), and Recall. Lower NFE indicates higher efficiency, lower FID denotes higher image quality, and higher Recall represents better mode coverage. The ‘Teacher’ row shows the performance of the original diffusion model which is being distilled.
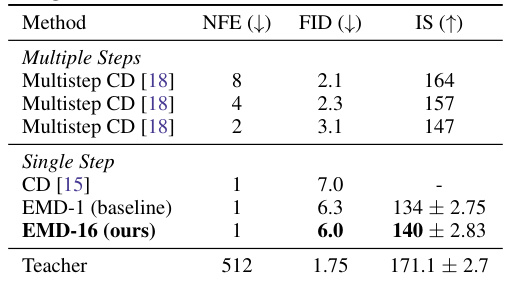
This table presents the results of class-conditional image generation on the ImageNet 128x128 dataset. It compares different methods, including multi-step and single-step approaches, in terms of their performance measured by FID (Frechet Inception Distance), IS (Inception Score), and NFE (number of forward evaluations). The table shows that the proposed EMD-16 method achieves competitive FID and IS scores with a significantly reduced number of forward evaluations compared to other methods.
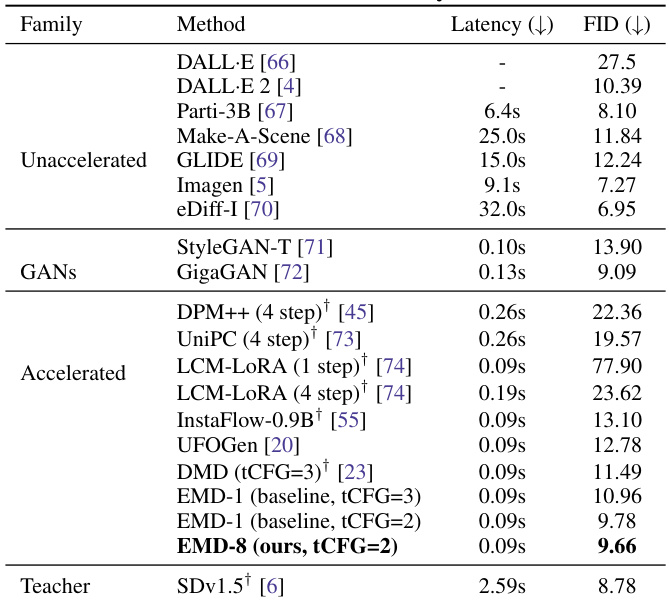
This table presents the FID scores for text-to-image generation on the MSCOCO dataset. The FID (Fréchet Inception Distance) is a metric used to evaluate the quality of generated images by comparing them to real images. Lower FID scores indicate better image quality. The table compares different methods, categorized into families (Unaccelerated, GANs, and Accelerated), showing their latency and FID scores. The results are evaluated using Yin et al. [23]’s method. The ‘Teacher’ row shows the performance of the Stable Diffusion v1.5 model, which is used as the base for comparison.

This table presents the CLIP scores achieved by various single-step and multi-step diffusion models on the text-to-image generation task. It specifically focuses on the performance in a high CFG (classifier-free guidance) regime, comparing the proposed EMD-8 method against other state-of-the-art accelerated diffusion sampling techniques, such as LCM-LORA and DMD. The table highlights the trade-off between inference speed (latency) and the quality of generated images (CLIP score), demonstrating EMD-8’s competitive performance in terms of both metrics.

This table shows the training time in seconds per step for different model variations. It compares the baseline Diff-Instruct method with various versions of the proposed EMD method (EMD-1, EMD-2, EMD-4, EMD-8, EMD-16). The variations involve different numbers of MCMC steps in the E-step and whether only student score matching or both student score matching and generator updates are used. The purpose is to analyze the computational cost introduced by the more complex sampling scheme in EMD compared to a simpler baseline.

This table shows the hyperparameters used for the EM Distillation (EMD) method on the ImageNet 64x64 dataset. It includes learning rates for the generator and score networks (lrg and lrs), batch size, Adam optimizer parameters (Adam b1 and b2), Langevin dynamics step sizes for epsilon and z (γe and γz), the number of MCMC steps (K), the target noise level (λ*), and the weighting function for the noise levels (w(t)). These parameters are crucial for controlling the training process and achieving optimal performance.

This table lists the hyperparameters used for training the EM distillation model on the ImageNet 128x128 dataset. It includes learning rates for the generator and score networks (lrg and lrs), batch size, Adam optimizer parameters (b1 and b2), step sizes for Langevin dynamics updates on epsilon and z (γε and γz), the number of Langevin steps (K), the target noise level (λ*), and the weighting function w(t).

This table lists the hyperparameters used for the EM Distillation (EMD) model when applied to text-to-image generation. It includes learning rates for the generator and score networks (lrg, lrs), batch size, Adam optimizer parameters (b1, b2), step sizes for Langevin dynamics (γe, γz), the number of Langevin steps (K), the specific noise level used (t*), and the weighting function for the loss (w̃(t)). These settings were crucial for achieving optimal performance in the text-to-image generation task.
Full paper#