↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Continual Reinforcement Learning (CRL) faces challenges like plasticity loss and primacy bias, hindering the ability of agents to learn new tasks effectively after being trained on previous tasks. These issues stem from the difficulty of optimizing deep neural networks when encountering non-stationary environments and changing objectives.
This paper introduces Parseval regularization, a method that encourages orthogonality in weight matrices of neural networks within RL agents. This helps to maintain favorable optimization properties during training. The authors show that Parseval regularization leads to improved performance on various RL tasks and propose other techniques to overcome the issues of limited network capacity and Lipschitz continuity.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the significant challenge of continual reinforcement learning (CRL). It proposes Parseval regularization, a novel technique to enhance the trainability and plasticity of neural networks in CRL settings. This work is highly relevant to current research focusing on improving the robustness and efficiency of deep learning models for sequential tasks and offers new avenues for exploration in optimization strategies and network architectures.
Visual Insights#
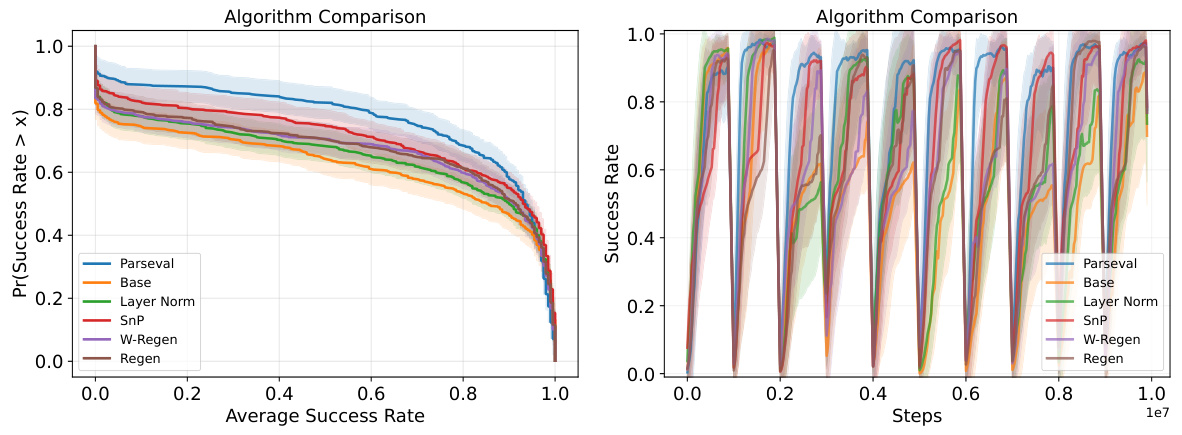
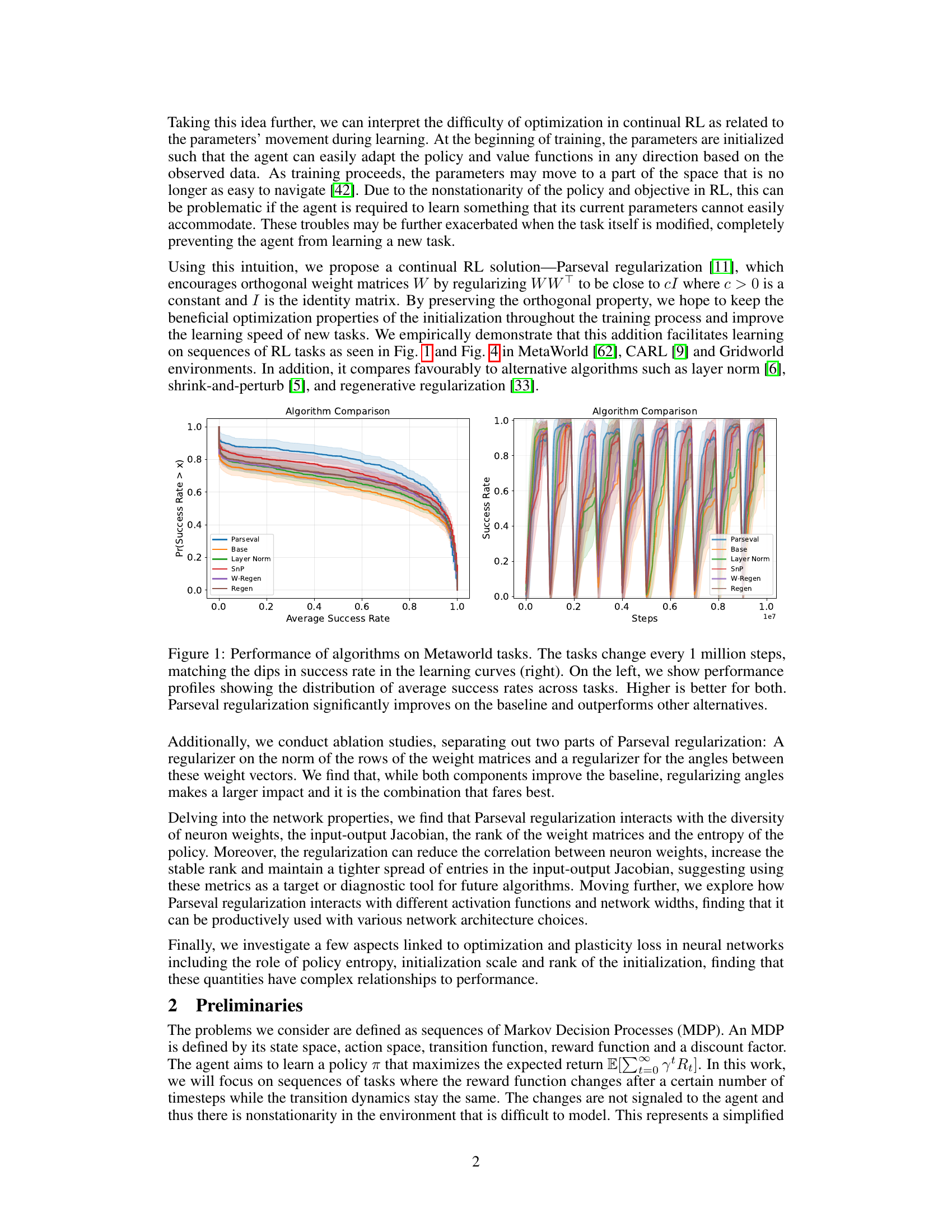
This figure displays a comparison of the performance of several reinforcement learning algorithms on MetaWorld tasks. The left panel presents performance profiles, showing the distribution of average success rates across various tasks for each algorithm. The right panel shows learning curves illustrating the success rate over time. The task changes every 1 million steps, which explains the dips in the success rate shown in the right panel. Parseval regularization demonstrates a significant improvement over baseline methods.

This table lists the 19 Metaworld tasks used in the Metaworld20-10 benchmark. These tasks were selected because the RPO agent achieved high success rates after 1 million training steps. The tasks represent a variety of manipulation challenges involving a robotic arm.
In-depth insights#
Parseval’s Promise#
Parseval’s theorem, when applied to weight matrices in neural networks, offers a compelling approach to continual reinforcement learning. Maintaining orthogonality among these matrices, as Parseval regularization encourages, is hypothesized to preserve beneficial optimization properties inherent in initial weight assignments. This prevents the detrimental effects of parameter drift during learning across multiple tasks, addressing issues like plasticity loss and primacy bias. The core promise lies in facilitating efficient learning of new tasks without catastrophic forgetting of previously learned ones, by keeping the weight matrices in regions conducive to optimization. Empirical results suggest significant performance gains, but further investigation is needed to fully understand the interplay between orthogonality, network architecture, and the specific continual learning challenges faced. Ablation studies are crucial to isolate the exact contribution of orthogonality versus other factors, enhancing the robustness and understanding of this technique.
Orthogonal Benefits#
The concept of orthogonality, particularly in the context of weight matrices within neural networks, offers compelling advantages in continual reinforcement learning. Orthogonal weight matrices ensure that the singular values of the matrices remain equal, preventing issues such as vanishing or exploding gradients that often hinder the training process in deep networks. This property, also linked to dynamical isometry, facilitates effective gradient propagation throughout the network, thus accelerating learning and enhancing stability. The research suggests that maintaining orthogonality, perhaps through Parseval regularization, is crucial for preserving the beneficial optimization characteristics of the initial network parameters throughout continual learning. By mitigating the negative impacts of non-stationarity and reducing the risk of catastrophic forgetting, the method improves the agent’s ability to adapt to subsequent tasks. While the imposition of strict orthogonality might limit network expressiveness, the addition of diagonal layers or input scaling successfully addresses this issue, enhancing the performance of the continual reinforcement learning model significantly.
Ablation Studies#
Ablation studies are crucial for isolating the impact of individual components within a complex system. In this research, the authors cleverly dissect Parseval regularization into its core elements: regularizing the norms of the weight matrix rows and constraining the angles between these row vectors. By separately testing each component, they demonstrate the relative importance of each contribution to overall performance. This systematic approach provides a deeper understanding than simply comparing the complete method against a baseline. The results highlight the significant role of angle regularization, suggesting that promoting diversity in weight vector directions is key. This finding offers valuable insights into the underlying mechanisms behind Parseval regularization’s effectiveness, paving the way for future improvements and modifications of the approach. Moreover, the ablation strategy effectively identifies the essential synergistic interaction between both components, emphasizing the importance of maintaining both orthogonal constraints for optimal results. Such a detailed analysis is vital for advancing understanding and future developments of this regularization technique.
Network Capacity#
The concept of network capacity within the context of neural networks is crucial for understanding their ability to learn complex functions. Orthogonal weight matrices, while beneficial for gradient flow, can be overly restrictive, potentially limiting the network’s capacity to express complex relationships. This limitation arises because orthogonal weight matrices enforce a Lipschitz continuity condition, meaning the function’s output cannot change too drastically with small changes in input. To mitigate this, the authors explore strategies to increase capacity, such as adding diagonal layers (introducing extra parameters) or scaling inputs. These methods help relax the Lipschitz constraint without sacrificing the benefits of orthogonality in terms of improved training dynamics. The results indicate that enhancing network capacity via these approaches maintains the advantages of Parseval regularization while avoiding limitations associated with strict orthogonality.
Future Work#
Future research directions stemming from this Parseval regularization work in continual reinforcement learning could explore several promising avenues. Extending the approach to more complex environments and tasks with varying dynamics would be crucial to assess its generalizability and robustness. Investigating its synergy with other continual learning techniques like experience replay or regularization methods would be valuable to potentially enhance performance further. A deeper theoretical understanding of Parseval’s impact on optimization dynamics, especially concerning the interplay between orthogonality, Lipschitz continuity, and plasticity, is needed. This could potentially lead to more principled ways to design continual learning algorithms. Empirical studies focusing on scalability to larger networks and more diverse task sequences should be carried out. Analyzing how Parseval regularization interacts with different network architectures (e.g., convolutional networks, transformers) would broaden its applicability. Finally, a thorough exploration of the relationship between Parseval regularization and other relevant metrics (e.g., Jacobian properties, weight diversity) is needed. This would not only consolidate existing findings but also guide the development of new and improved continual learning techniques.
More visual insights#
More on figures
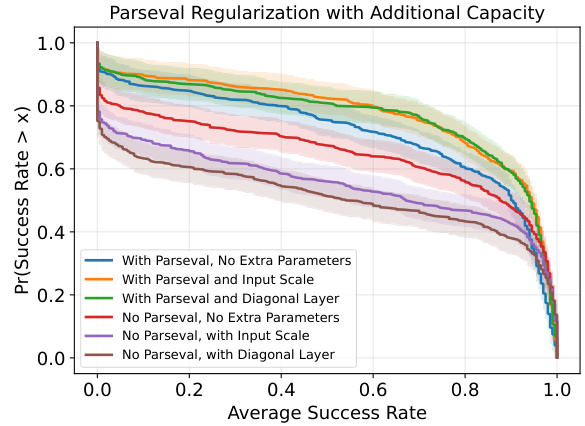
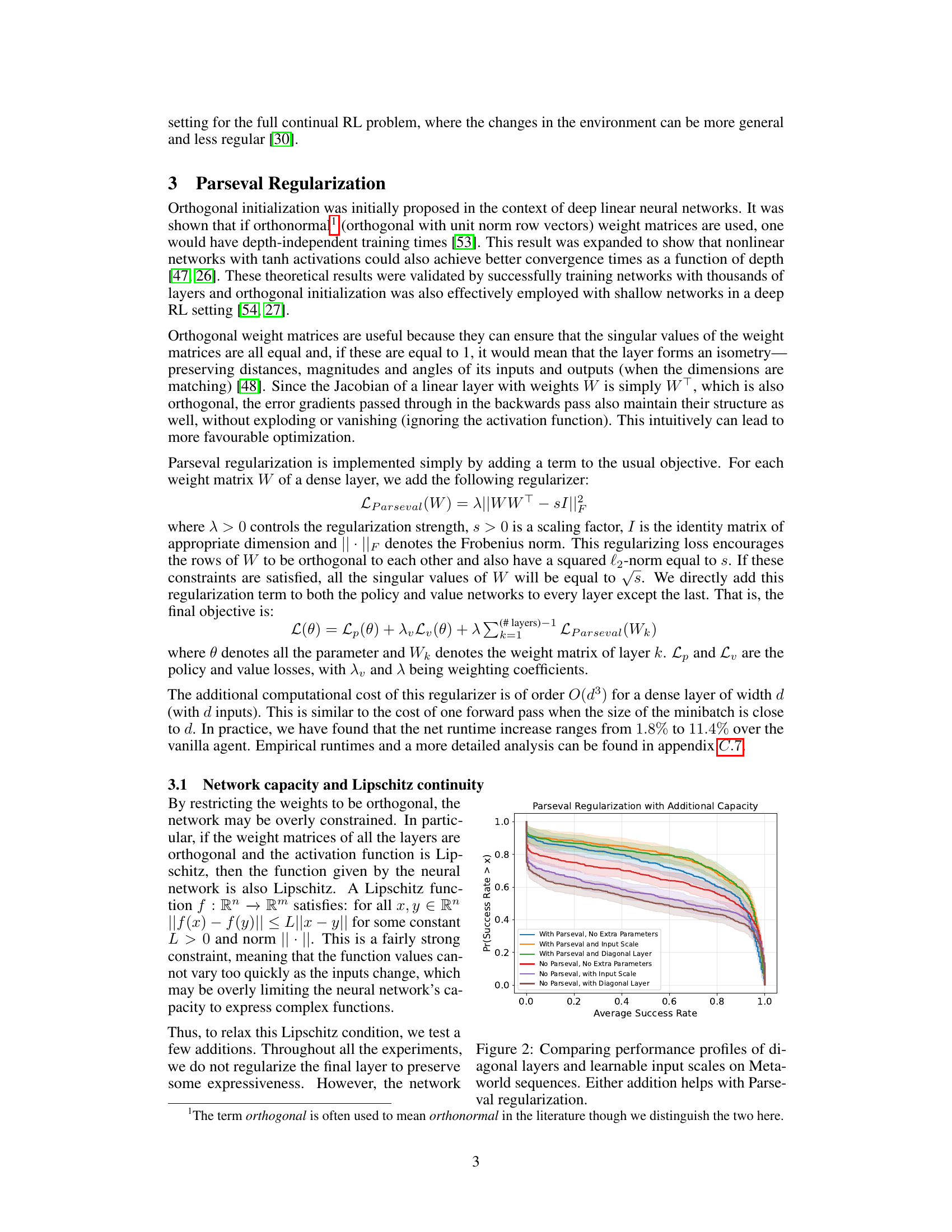
This figure compares the performance of different approaches to enhance the capacity of neural networks using Parseval regularization in a continual reinforcement learning setting on MetaWorld tasks. It shows performance profiles, illustrating the distribution of average success rates across multiple tasks. The results demonstrate that adding either diagonal layers or a learnable input scale improves performance when using Parseval regularization, although these additions alone are detrimental to the baseline agent’s performance.
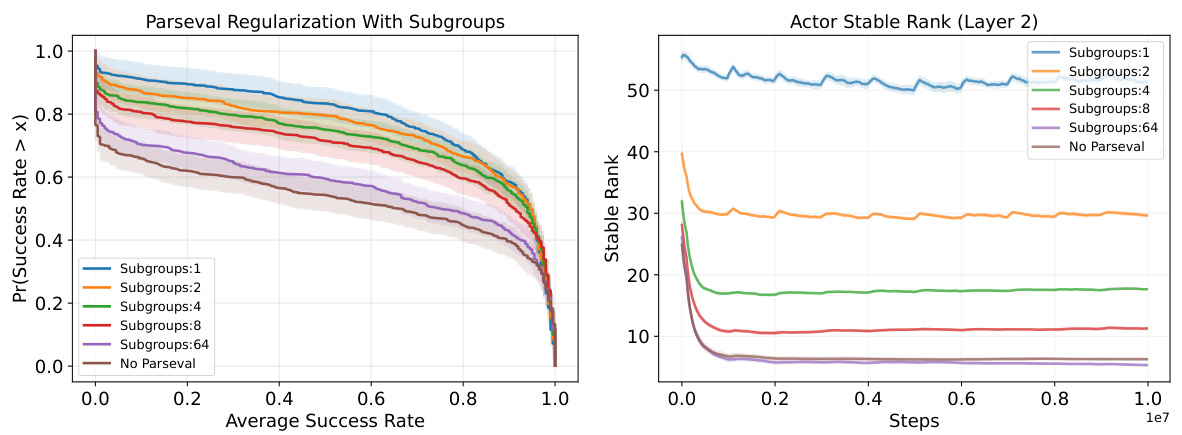
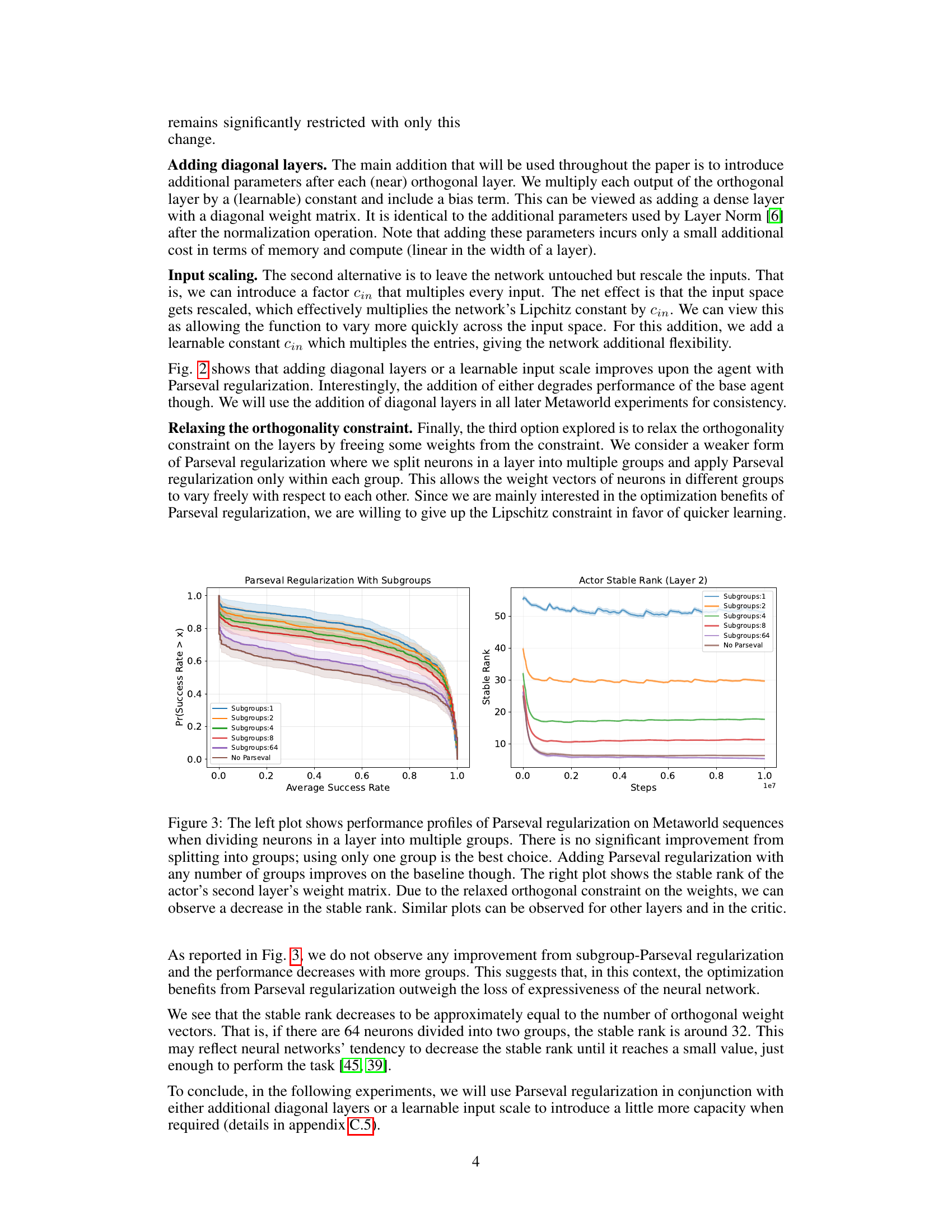
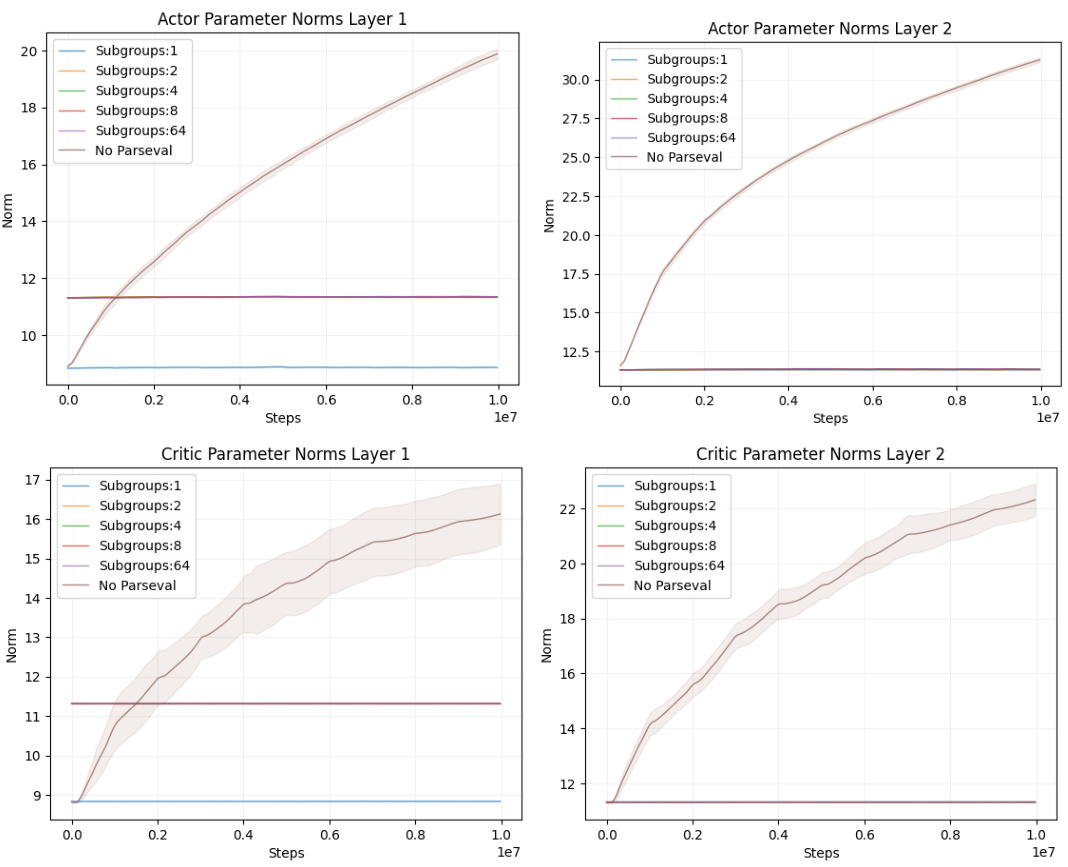
The figure shows the impact of dividing neurons in a layer into subgroups on the performance of Parseval regularization in a continual reinforcement learning setting using Metaworld tasks. The left plot presents performance profiles, showing that dividing neurons into subgroups doesn’t significantly improve performance compared to using a single group; however, Parseval regularization consistently outperforms the baseline regardless of the number of subgroups. The right plot displays the stable rank of the second layer’s weight matrix for the actor network across different subgroup configurations and the baseline. A decreased stable rank is observed with multiple subgroups, indicating a relaxation in the orthogonality constraint imposed by Parseval regularization.

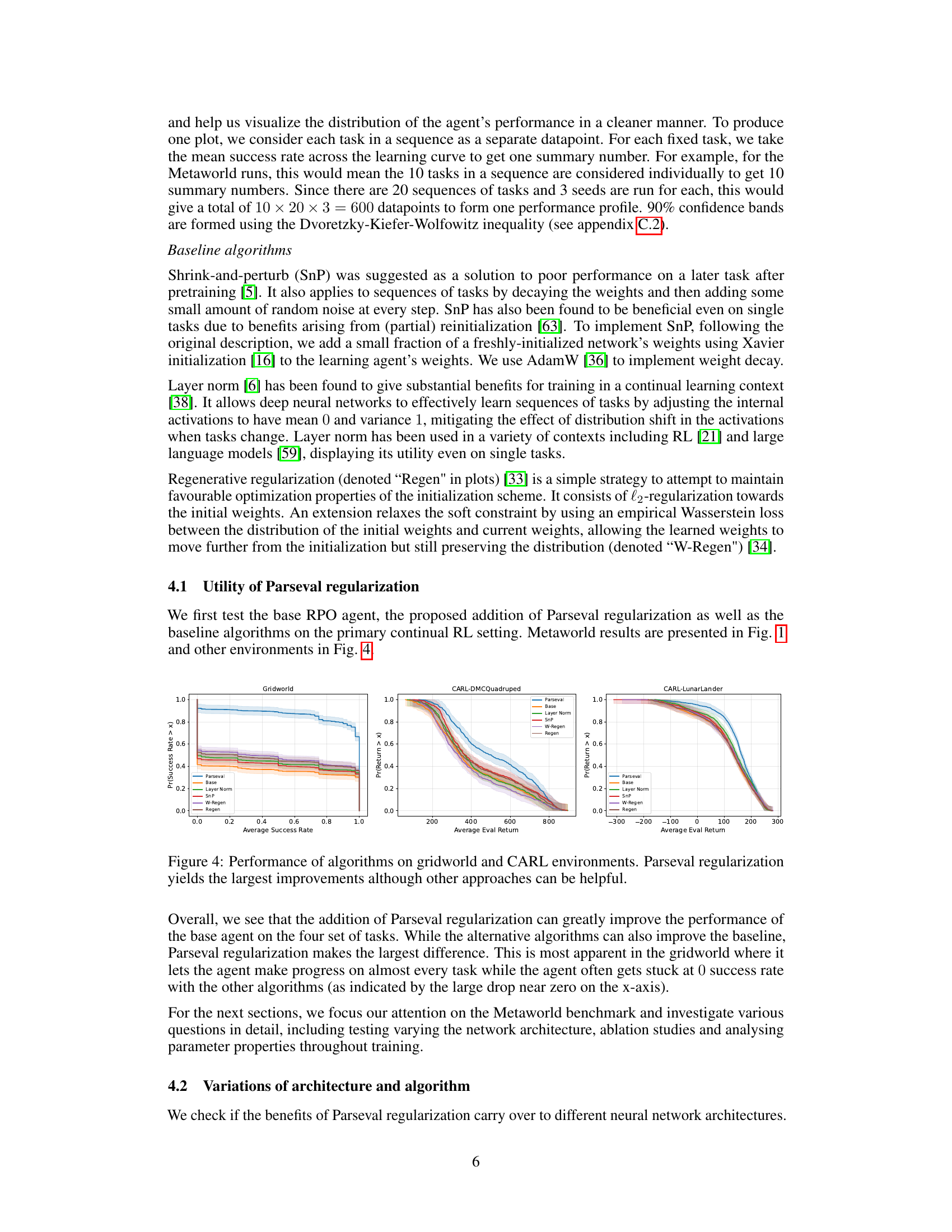
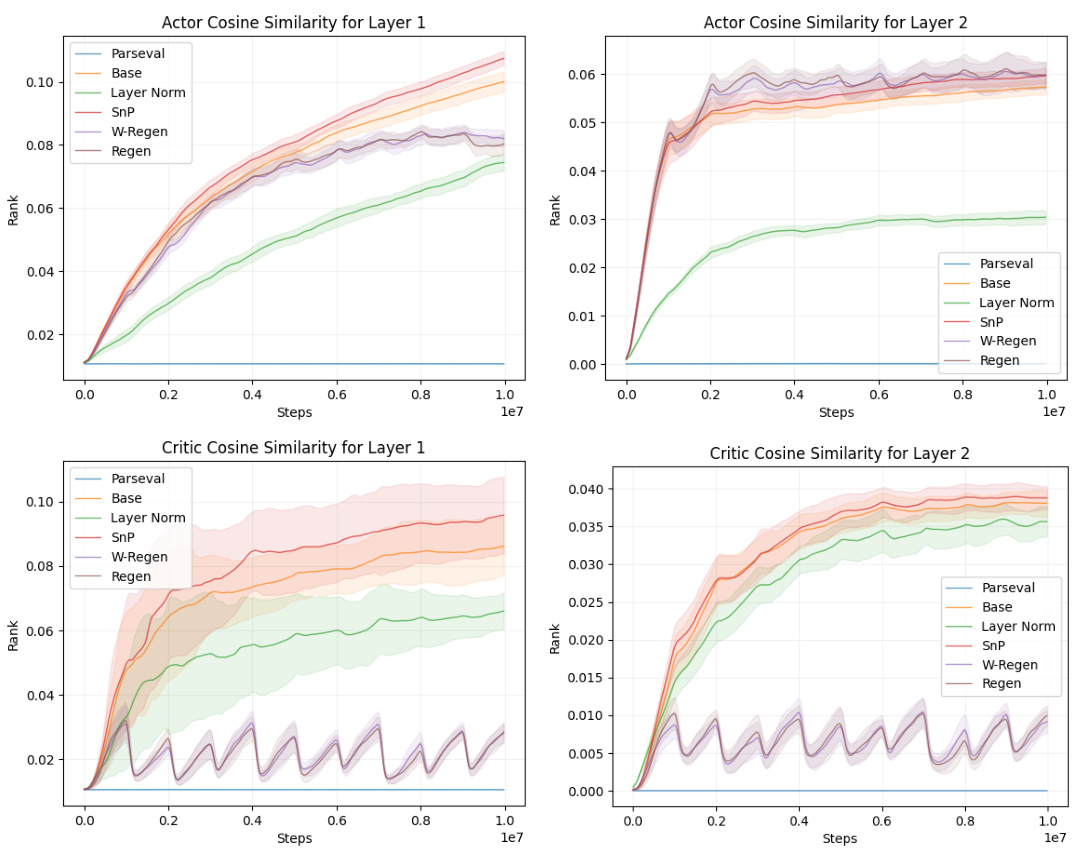
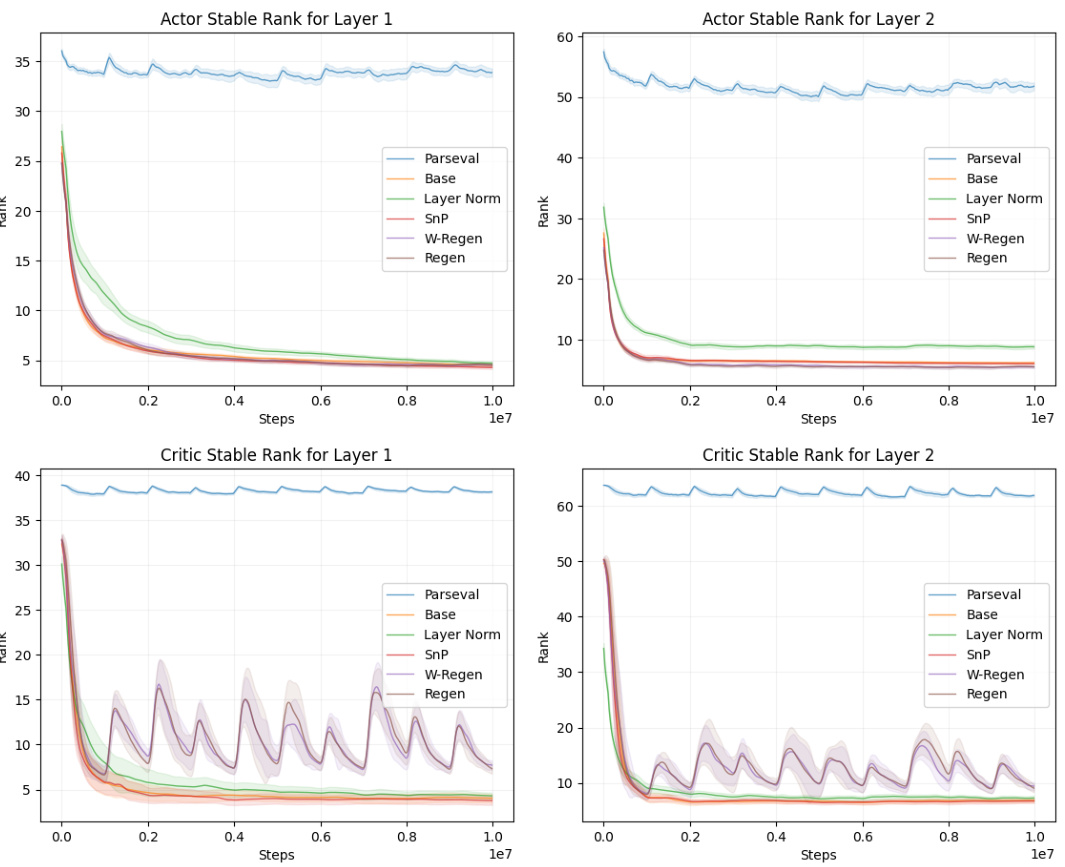
This figure compares the performance of several continual reinforcement learning algorithms across two different environments: a gridworld navigation task and two tasks from the CARL (Contextual and Adaptive Reinforcement Learning) benchmark. The algorithms compared include a baseline (base) agent, along with Layer Normalization (Layer Norm), Shrink-and-Perturb (SnP), Regenerative Regularization (Regen), and a Wasserstein-distance based variant of Regen (W-Regen). The figure highlights the substantial improvement achieved by Parseval regularization in both environments, showcasing its effectiveness in continual learning settings. While other methods show some improvement over the baseline, none reach the level of Parseval regularization’s performance boost.

This figure presents the results of ablation studies on different neural network architectures. The left and center plots show how different activation functions (Tanh, ReLU, Mish, CReLU, MaxMin) perform with and without Parseval regularization. The right plot compares the performance of networks with different widths (32, 64, 128) with and without Parseval regularization. The results demonstrate that Parseval regularization consistently improves performance across different activation functions and network widths, whereas simply increasing network width has minimal impact.
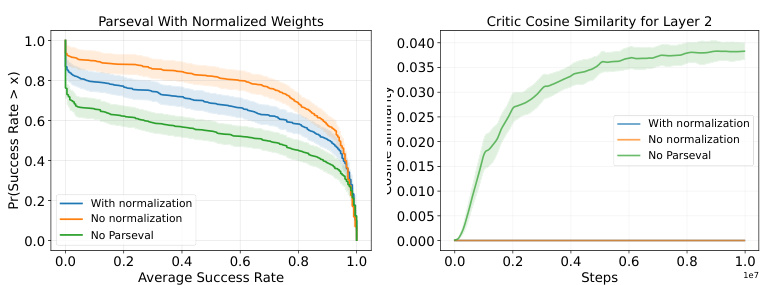
This figure presents ablation studies on Parseval regularization, focusing on the impact of normalizing row weights before applying the regularization. The left panel shows the performance profiles demonstrating that while there is some improvement over the baseline, it’s not as significant as the full Parseval regularization. The right panel shows the average angle between row weight vectors over training steps. It confirms the efficacy of the modified regularization in encouraging orthogonality by keeping the average angle near zero.
This figure compares the performance of different algorithms on Metaworld tasks in a continual reinforcement learning setting. The left panel shows performance profiles, illustrating the distribution of average success rates across multiple tasks. The right panel displays learning curves showing success rate over training steps. The tasks change every 1 million steps, leading to dips in performance. Parseval regularization significantly improves both the average success rate and the learning curve, outperforming other methods.

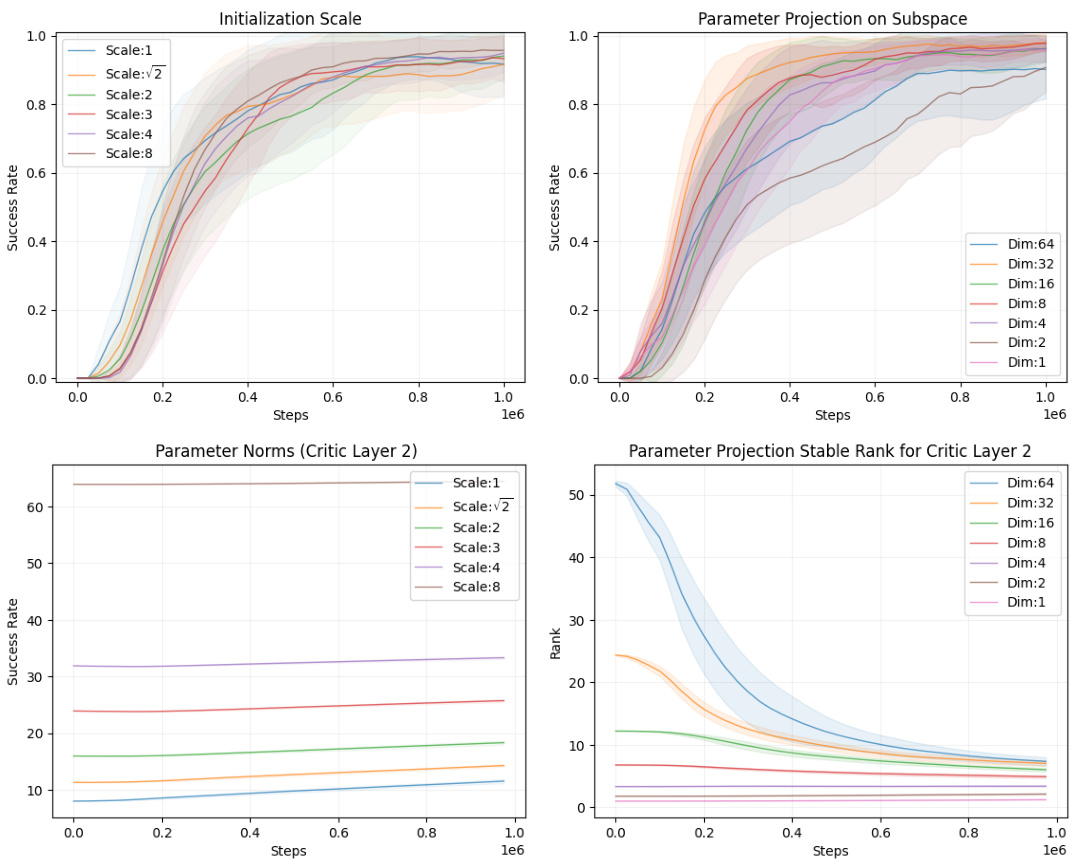
This figure compares the performance of two different initialization scales (1 and sqrt(2)) with and without Parseval regularization. The performance profiles show the probability that an agent achieves a success rate greater than or equal to a given average success rate across different tasks. The results indicate that Parseval regularization mitigates the effect of different initialization scales on performance, leading to similar results regardless of the chosen scale.

This figure shows the effect of entropy regularization on continual reinforcement learning. The left subplot displays learning curves for different entropy regularization strengths, illustrating the impact on the success rate. The right subplot shows how policy entropy changes across various algorithms over time, highlighting the relationship between entropy and performance.
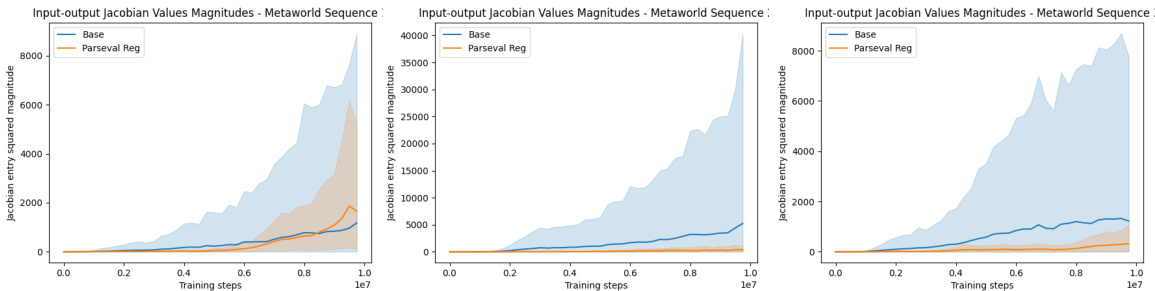
This figure displays the distribution of squared entries in the input-output Jacobian over training for three different Metaworld task sequences. The plots show that Parseval regularization results in a tighter distribution of these magnitudes compared to the baseline, suggesting that it may contribute to a less difficult optimization landscape.
The figure compares the performance of different algorithms on Metaworld tasks in a continual reinforcement learning setting. The left panel shows performance profiles illustrating the distribution of average success rates across various tasks for each algorithm. The right panel displays learning curves showing the success rate over time. The tasks switch every million steps, causing dips in the success rate curves, highlighting the challenge of continual learning. Parseval regularization shows a significant improvement over baseline and other methods.
This figure displays a comparison of different reinforcement learning algorithms’ performance on Metaworld tasks. The left panel shows performance profiles, illustrating the distribution of average success rates across multiple tasks. Each point represents the average success rate for a single task in a sequence of tasks. The right panel shows learning curves, plotting the success rate over time. These curves demonstrate how the success rate dips when a new task is introduced, indicating the challenge of continual learning. The Parseval regularization method shows improved performance compared to baseline and alternative methods (Layer Norm, Shrink-and-Perturb, Regenerative regularization) in both metrics.
This figure compares the performance of different algorithms on Metaworld tasks in a continual reinforcement learning setting. The tasks change every 1 million steps. The left panel shows performance profiles, illustrating the distribution of average success rates across all tasks for each algorithm. The right panel provides the learning curves showing the success rate over time. Parseval regularization shows significant improvement over baseline and other methods.

This figure presents performance profiles that compare the effects of different activation functions (Tanh, ReLU, Mish, and MaxMin) and network widths on continual reinforcement learning agents. The left and center plots show that adding Parseval regularization improves performance regardless of the activation function used. The right plot demonstrates that Parseval regularization enhances performance across different network widths, while simply increasing the network width without Parseval regularization does not provide the same benefit.
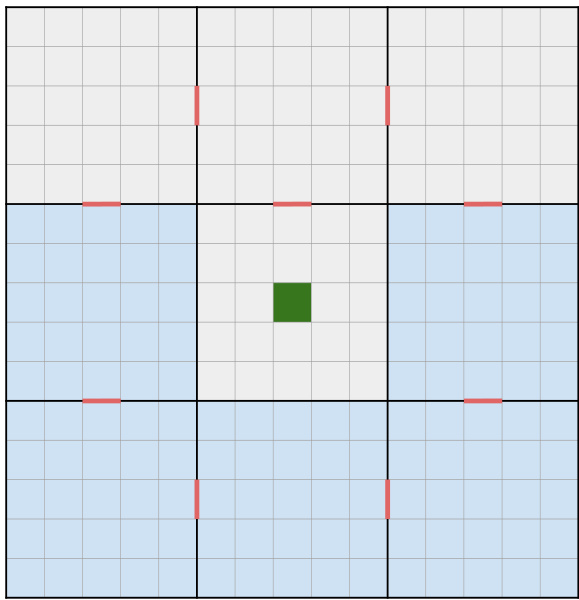
This figure shows the layout of the 15x15 gridworld environment used in the experiments. The grid is divided into nine rooms connected by doorways. The agent begins each episode at the green square in the center. A goal location, represented by a blue shaded area, is randomly selected within one of the rooms at the start of each episode and remains fixed until the task changes. Then, a new goal location is randomly selected. This setup allows for a sequence of tasks, where the agent needs to navigate to different goal locations across episodes.
More on tables
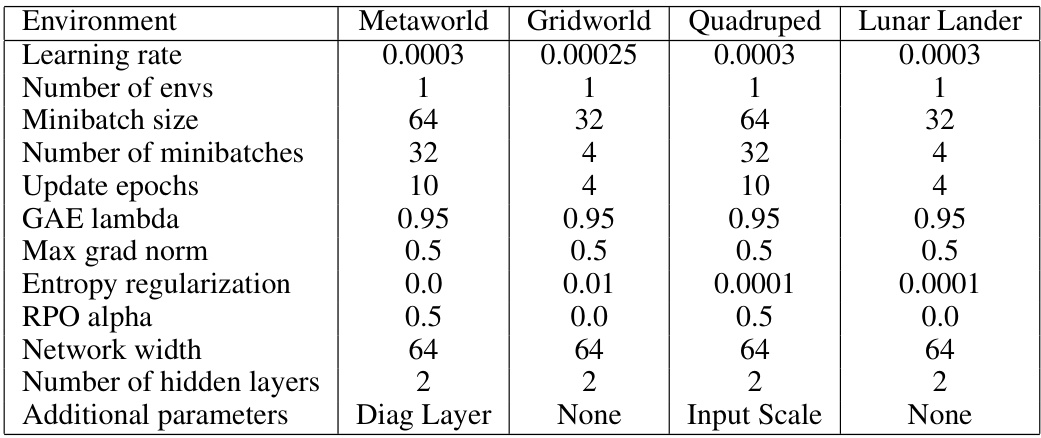
This table shows the hyperparameters used for both the RPO and PPO algorithms across four different reinforcement learning environments: Metaworld, Gridworld, Quadruped, and Lunar Lander. For each environment, the table lists the learning rate, number of environments, minibatch size, number of minibatches, update epochs, GAE lambda, maximum gradient norm, entropy regularization, RPO alpha, network width, number of hidden layers, and the type of additional parameters used (Diagonal Layer, None, Input Scale). The hyperparameters were tuned for optimal performance in each environment.

This table presents the runtimes for different algorithms across four different continual reinforcement learning environments. The runtimes are given in minutes for each algorithm (no Parseval regularization, with Parseval regularization, and shrink-and-perturb). The percentage increase in runtime for Parseval regularization compared to the no-Parseval baseline is provided. The data highlights that Parseval regularization adds minimal computational overhead compared to the baseline and even slightly less than the shrink-and-perturb method.
Full paper#