↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline Reinforcement Learning (RL) faces challenges due to data distribution issues; behavior regularization, though simple, often struggles with suboptimal policies. Existing methods often suffer from extrapolation errors when dealing with out-of-distribution data, leading to poor performance.
This paper introduces Iteratively Refined Behavior Regularization, enhancing behavior regularization via iterative policy refinement. This approach implicitly prevents querying out-of-sample actions and guarantees policy improvement. The algorithm’s effectiveness is proven theoretically (for tabular settings) and empirically, demonstrating superior performance on D4RL benchmarks compared to state-of-the-art baselines.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel offline reinforcement learning algorithm that significantly improves the robustness and efficiency of behavior regularization. This addresses a key challenge in offline RL, where learning from limited and potentially suboptimal data is difficult. The proposed method’s simplicity and effectiveness, demonstrated through extensive experiments, make it highly relevant to current RL research and a valuable tool for practitioners.
Visual Insights#
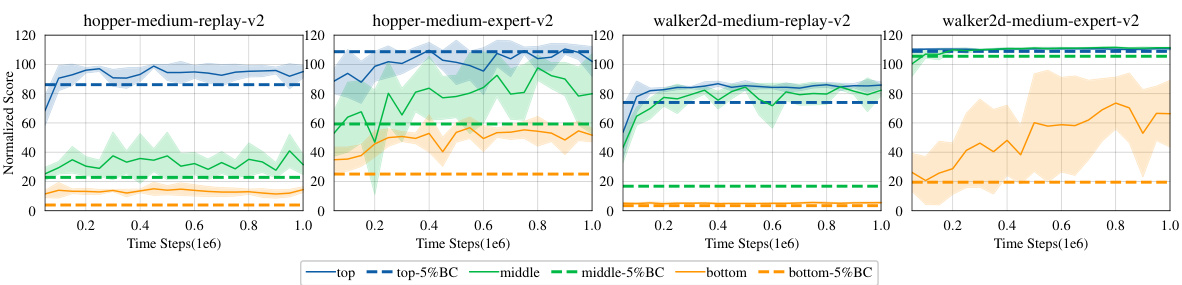
This figure shows the performance comparison between behavior cloning and behavior regularization using TD3 algorithm. Four different D4RL environments are used. The dashed lines represent the performance of reference policies trained on subsets of the data (top 5%, middle 5%, bottom 5% of trajectories based on performance). The solid lines show the TD3 performance when using these different reference policies for regularization. The results demonstrate that behavior regularization generally outperforms behavior cloning, and its effectiveness heavily depends on the quality of the reference policy used.

This table presents a comparison of the average normalized scores achieved by the proposed CPI algorithm and several existing offline reinforcement learning methods across various datasets from the D4RL benchmark. The results are presented with mean and standard deviation, and the top three performing methods for each dataset are highlighted in bold. The table also highlights that CPI achieves the best overall performance and requires fewer computational resources.
In-depth insights#
Offline RL Robustness#
Offline reinforcement learning (RL) faces the challenge of ensuring robustness to data distribution, particularly when the training data originates from a suboptimal policy. Behavior regularization, a common approach, attempts to mitigate this by penalizing deviations from the behavior policy used to collect the data. However, its effectiveness is highly contingent on the quality of the behavior policy. A key issue is that suboptimal behavior policies can lead to poor performance, and the learned policy may not generalize well to unseen situations. This limitation highlights the need for more advanced techniques that enhance robustness and generalization, either by iteratively refining the reference policy or using more sophisticated methods such as in-sample optimality or distribution correction. Future research should explore more robust methods that can effectively leverage offline data, regardless of its origin, ensuring that the learned policies are both effective and generalizable. This involves careful consideration of data quality, distribution shift, and out-of-distribution generalization.
CPI Algorithm#
The Conservative Policy Iteration (CPI) algorithm, as presented in the research paper, is a novel approach to offline reinforcement learning. It directly addresses the limitations of traditional behavior regularization by iteratively refining the reference policy. This iterative refinement process implicitly avoids out-of-distribution actions, a common pitfall in offline RL, while ensuring continuous policy improvement. A key theoretical finding is that, in the tabular setting, CPI is capable of converging to the optimal in-sample policy. The algorithm’s practical implementation incorporates function approximations and is designed for ease of use, requiring minimal code modifications to existing methods. Experimental results demonstrate that CPI significantly outperforms state-of-the-art baselines across various benchmark tasks, highlighting its robustness and efficiency. Importantly, the algorithm’s effectiveness stems from its ability to skillfully balance exploration and exploitation through conservative updates, thereby preventing catastrophic failures often associated with out-of-distribution state-action exploration.
Empirical Analysis#
An Empirical Analysis section in a research paper would rigorously evaluate the proposed offline reinforcement learning algorithm. It would likely involve experiments across various benchmark tasks from the D4RL suite, comparing the algorithm’s performance against several established baselines (e.g., behavior cloning, conservative Q-learning). Key metrics would include average return per episode, demonstrating the algorithm’s ability to learn effective policies from offline data. A crucial aspect would be analyzing the algorithm’s robustness to different data distributions, potentially using datasets generated by near-optimal or suboptimal policies. The analysis might delve into the algorithm’s sensitivity to hyperparameter settings, providing insights into optimal configurations and their effect on performance. Visualizations, such as learning curves, would be essential to show the algorithm’s convergence behavior and its stability over different tasks. Statistical significance testing would provide confidence in the observed results, ensuring that reported improvements are not merely due to random chance. Finally, the analysis should address computational aspects, comparing the algorithm’s training speed and memory requirements against the baselines. This comprehensive evaluation would build confidence in the algorithm’s effectiveness and highlight its strengths and weaknesses compared to existing approaches.
Ablation Studies#
Ablation studies systematically remove components of a model to assess their individual contributions. In the context of the described research, this would involve investigating the impact of removing or altering specific elements of the Iteratively Refined Behavior Regularization (IRBR) algorithm. Key areas for ablation would include the iterative refinement process itself, testing variations on the frequency or method of updating the reference policy. Another crucial aspect would be the behavior regularization component, experimenting with different regularization strengths or alternative regularization methods. Analyzing the effect of the conservative policy update rule is also critical, evaluating the impact of relaxing this constraint on the model’s stability and performance. The choice of KL divergence is another point of focus, comparing reverse KL with other options and investigating the impact on performance. The function approximation techniques would also be investigated to assess robustness under various settings. By carefully examining the effects of these individual components, the researchers can pinpoint which aspects of the method are most essential and which are less critical, providing crucial insights into the algorithm’s functioning and potential areas for future improvement.
Future Work#
Future research could explore several promising avenues. Extending the Iteratively Refined Behavior Regularization (CPI) algorithm to handle more complex environments with continuous state and action spaces would be valuable. Investigating the impact of different function approximation techniques on CPI’s performance, potentially exploring more advanced architectures beyond actor-critic methods, is warranted. Furthermore, a more comprehensive theoretical analysis of CPI’s convergence properties in non-tabular settings could solidify its foundations. Finally, applying CPI to other offline reinforcement learning challenges such as those involving sparse rewards or safety constraints would broaden its applicability and practical impact.
More visual insights#
More on figures
This figure shows the performance of TD3 with different reference policies trained on sub-datasets with varying performance levels (top 5%, median 5%, bottom 5%). The results demonstrate that behavior regularization outperforms behavior cloning, and its effectiveness heavily depends on the quality of the reference policy used.
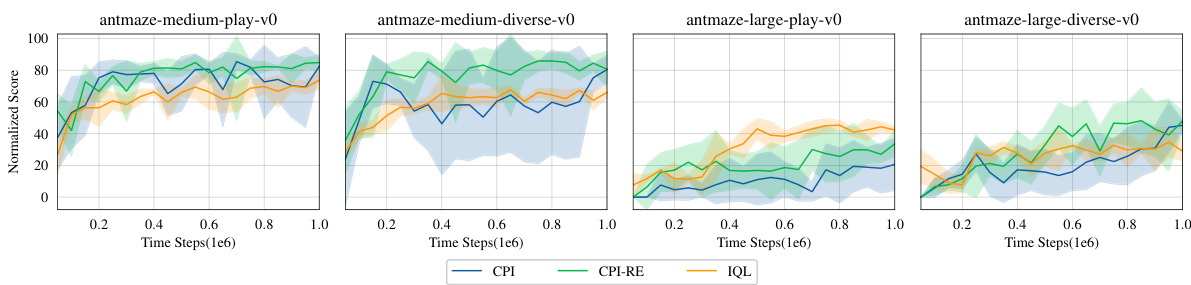
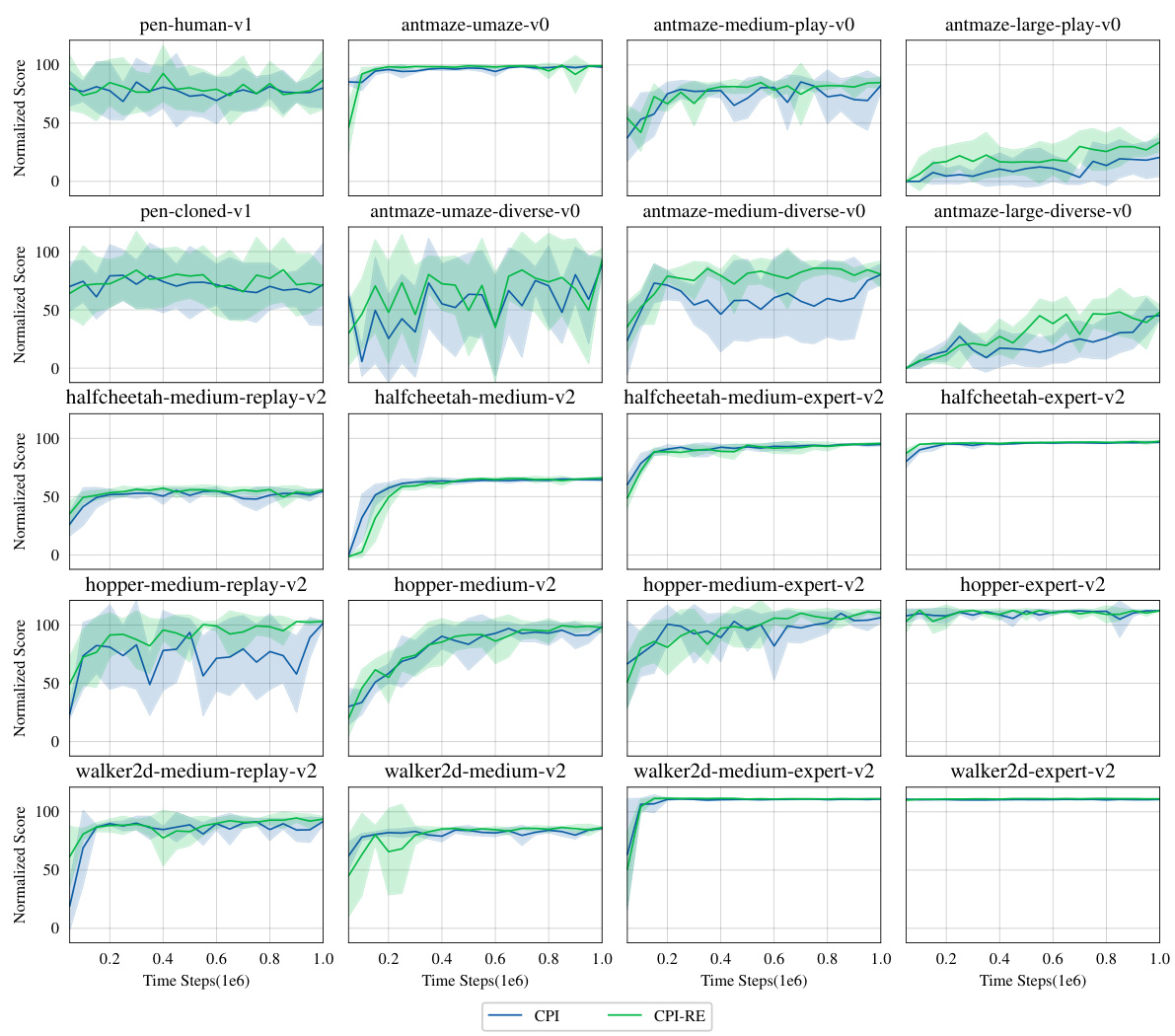
This figure compares the training performance of three algorithms: CPI, CPI-RE, and IQL, on four different Antmaze environments. The x-axis represents the number of time steps (in millions) during training, and the y-axis represents the normalized score achieved by each algorithm. The shaded area around each line indicates the standard deviation across multiple runs. The results show that CPI-RE, which uses an ensemble of reference policies, consistently outperforms both CPI and IQL in terms of stability and final performance. CPI-RE demonstrates smoother learning curves with less variance than CPI, highlighting the benefit of using an ensemble of reference policies for improving robustness and efficiency. The superior performance of CPI-RE over IQL further suggests that the iterative refinement of the reference policy, a key aspect of the proposed CPI algorithm, is crucial for achieving strong performance in offline reinforcement learning.
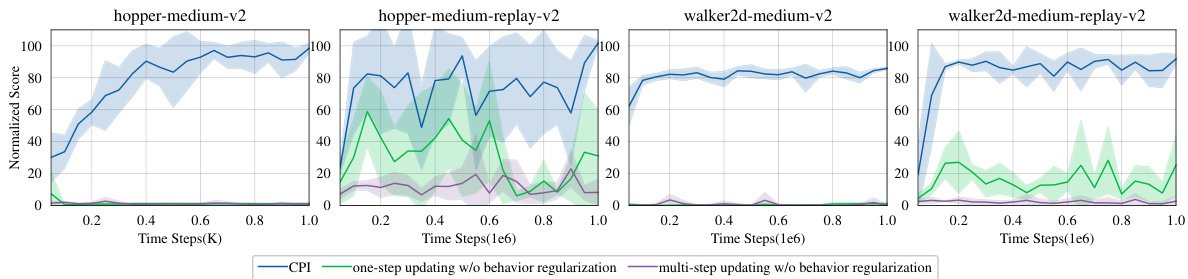
This figure compares the performance of CPI with and without behavior regularization using one-step and multi-step updating methods. The results demonstrate that omitting behavior regularization leads to significant performance degradation, particularly when using multi-step updates. This highlights the crucial role of behavior regularization in constraining the policy to the support of the offline data and preventing catastrophic failures from out-of-distribution state-action pairs.

This figure shows the impact of using behavior regularization in the CPI algorithm. It compares the performance of CPI with behavior regularization against versions that omit it and use either one-step or multi-step updating methods. The results demonstrate that without behavior regularization, the algorithm’s policy updates can lead to significant deviations from the supported data, ultimately hindering performance. The inclusion of behavior regularization helps to constrain the updates to stay within the valid state-action space, resulting in improved stability and performance.

This figure shows the ablation study on two hyperparameters: λ (weighting coefficient) and τ (regularization hyperparameter). The left panel shows how different values of λ impact performance across four Mujoco tasks. The right panel shows the impact of τ across those same four tasks. The results suggest that λ = 0.5 or 0.7 is generally effective, and that τ should be larger for higher-quality datasets.

This figure shows the results of online finetuning of several offline reinforcement learning algorithms on nine Mujoco tasks from the D4RL benchmark. The algorithms compared are TD3+BC, IQL, PEX, Cal-QL, CPI, and CPI-RE. The y-axis represents the normalized score, and the x-axis represents the number of time steps (in thousands). The shaded regions around the lines indicate the standard deviation across multiple runs. The figure demonstrates that CPI and CPI-RE achieve superior performance compared to other methods after online finetuning.
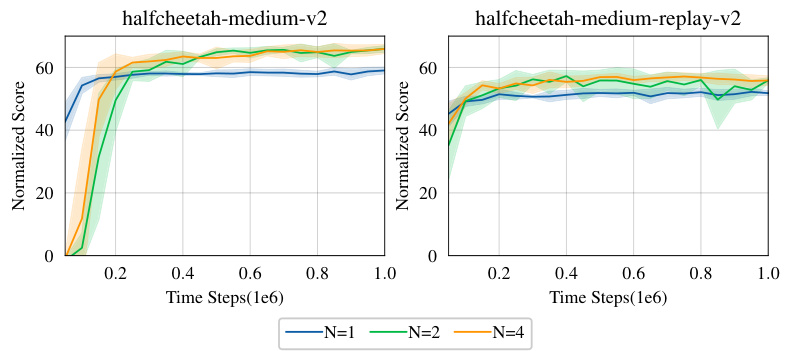
This figure shows the effect of using different numbers of actors in the CPI-RE algorithm. The x-axis represents the time steps (in millions) during training, and the y-axis represents the normalized score achieved. Three lines are plotted, each corresponding to a different number of actors (N=1, N=2, N=4). The results indicate that increasing the actor number from 1 to 2 significantly improves the performance, while further increasing the number of actors does not bring significant additional benefits and might increase resource consumption. Therefore, the optimal number of actors for the CPI-RE algorithm is 2.

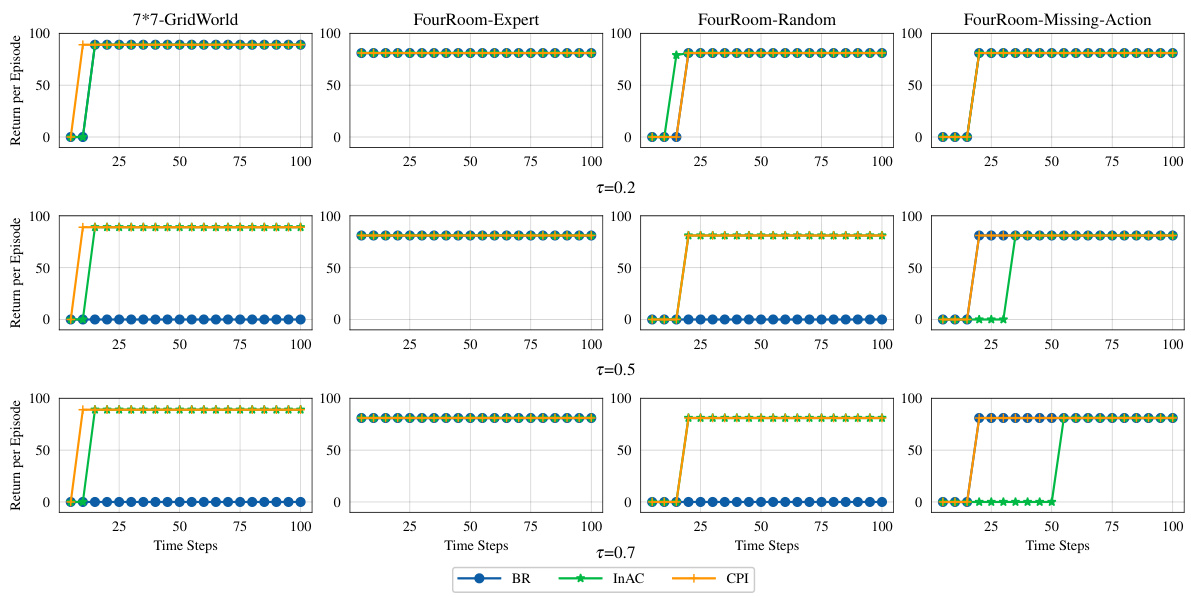
The figure shows the training curves for three algorithms: BR, InAC, and CPI on two gridworld environments (7x7-GridWorld and FourRoom). It compares their performance in reaching the goal state from different starting locations. The x-axis represents the training steps, and the y-axis represents the normalized return per episode. The results demonstrate that CPI and InAC converge to the optimal policy (oracle), while BR shows suboptimal performance. This highlights CPI’s ability to find the optimal policy within the provided offline data.
The figure shows the training performance curves of three different offline reinforcement learning (RL) algorithms on two different grid environments (7x7 GridWorld and FourRoom). The algorithms compared are Behavior Regularization (BR), In-sample optimal policy algorithm (InAC), and the proposed algorithm, Conservative Policy Iteration (CPI). The plots demonstrate how the cumulative return (reward) changes over the course of training. The results indicate that CPI and InAC achieve similar performance and reach the optimal policy, while BR lags behind.
More on tables

This table presents the average normalized scores achieved by CPI and other baseline algorithms across various tasks in the D4RL benchmark. The results are presented with mean and standard deviation, and the top three results for each task are highlighted in bold. The table highlights CPI’s superior performance and efficiency compared to the baselines.

This table presents a comparison of the average normalized scores achieved by the proposed CPI algorithm and several other baseline methods on various tasks from the D4RL benchmark. The table includes the mean and standard deviation for each method’s performance on each dataset. The top three performing methods are highlighted in bold for each dataset, demonstrating the superior performance of CPI.

This table compares the average normalized scores achieved by the proposed CPI algorithm and several other state-of-the-art offline reinforcement learning methods on various D4RL benchmark datasets. The results are presented with mean and standard deviation, highlighting CPI’s superior performance and computational efficiency. Top 3 results are emphasized in bold.

This table presents a comparison of the proposed CPI algorithm’s performance against several existing offline reinforcement learning methods on the D4RL benchmark. The table shows the average normalized scores (mean ± standard deviation) achieved by each algorithm on various tasks, highlighting CPI’s superior performance and efficiency.
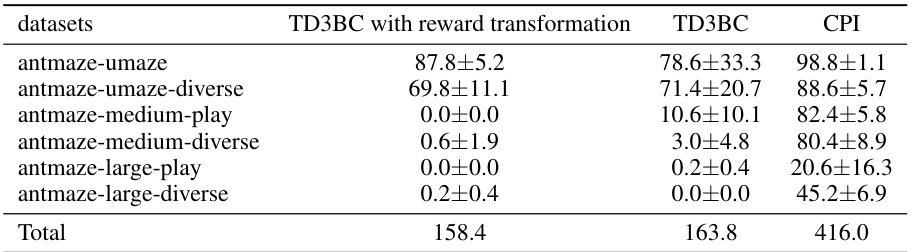
This table presents the average normalized scores achieved by CPI and various other offline reinforcement learning methods across multiple D4RL benchmark datasets. The results include the mean and standard deviation for CPI, highlighting its superior performance and computational efficiency compared to other methods. Top 3 results for each dataset are emphasized.

This table presents the average normalized scores achieved by CPI and several other offline reinforcement learning algorithms across various tasks from the D4RL benchmark. The scores are normalized, and the top three results for each task are highlighted in bold. The table also shows that CPI achieves the best overall performance while using relatively few computing resources.

This table presents the average normalized scores achieved by CPI and several other offline reinforcement learning algorithms across various D4RL benchmark tasks. It compares the performance of CPI against state-of-the-art baselines, highlighting CPI’s superior performance and efficiency in terms of computation time. The table includes the mean and standard deviation of the results, and the top three results for each dataset are bolded.

This table compares the average normalized scores achieved by the proposed CPI algorithm and several other state-of-the-art offline reinforcement learning algorithms on various D4RL benchmark datasets. The table highlights the superior performance of CPI in terms of average normalized scores, while also pointing out its computational efficiency. The top three performing algorithms for each dataset are marked in bold.

This table presents the average normalized scores achieved by CPI and other state-of-the-art offline reinforcement learning methods on various D4RL benchmark tasks. The scores are normalized, and the top three results for each task are highlighted in bold. The table also indicates that CPI outperforms other methods while requiring fewer computational resources.
Full paper#



















