Neural Persistence Dynamics

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it offers a novel approach to analyzing collective behavior, overcoming limitations of previous methods that rely on tracking individual entities. Its scalability and accuracy make it relevant to various fields, opening new avenues for research and application in collective dynamics.

Visual Insights

#

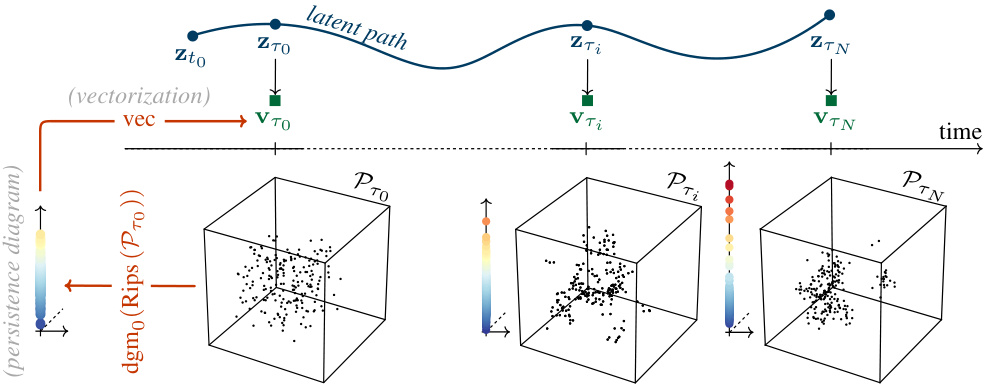
This figure illustrates the Neural Persistence Dynamics (NPD) framework. It starts with a time series of point clouds representing collective behavior. Each point cloud is processed using persistent homology to generate a persistence diagram, which summarizes the topological features of the point cloud. These diagrams are then vectorized into a numerical representation. The NPD framework then models the dynamics of these vectorized persistence diagrams using a latent ordinary differential equation (ODE). Finally, a regression model is used to predict the parameters of the governing equations that describe the collective behavior based on the latent ODE’s output.

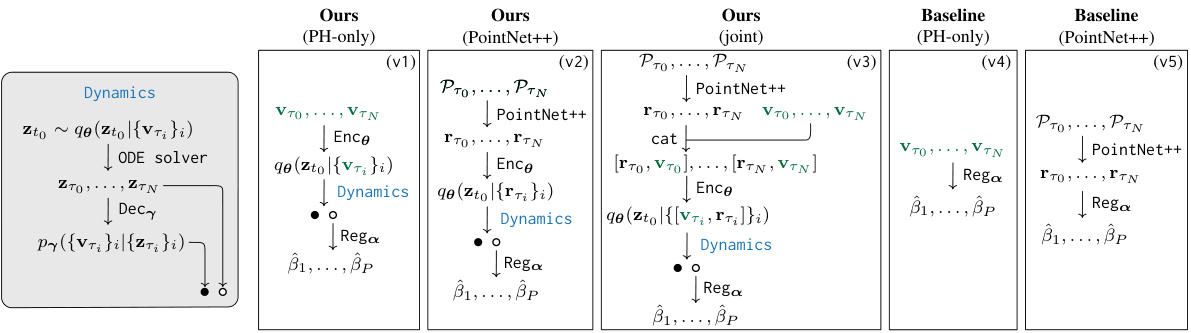
This table compares the performance of using PointNet++ and persistent homology (PH) for representing point cloud data in a parameter regression task. The results demonstrate the effectiveness of PH, especially in the vicsek-10k dataset, where it significantly outperforms PointNet++. This highlights the potential benefits of topological features over traditional point cloud methods in analyzing collective behavior.

In-depth insights

#

Topological Dynamics

#

Topological dynamics, in the context of this research paper, likely involves studying the evolution of topological features within a system, specifically focusing on how those features change over time. This approach moves beyond traditional methods, which might rely on tracking individual entities or particles, by analyzing the overall shape and structure of the system. Key aspects could include using persistent homology to extract topological summaries (like persistence diagrams) at different time points, then modeling the dynamics of these summaries over time. This may involve using techniques like latent ordinary differential equations (ODEs) to capture continuous changes or other methods depending on the nature of the data. The primary benefit lies in its robustness to the challenges of tracking individual entities in large, complex systems, allowing for the study of collective behavior without requiring detailed trajectories for each component. A critical consideration would be the stability of the chosen topological summaries and the methods used to model the dynamics, ensuring that small changes in the system lead to only small changes in the derived model. This is crucial to ensure the reliability and meaningful interpretation of the findings.

Latent ODE Modeling

#

Latent Ordinary Differential Equation (ODE) modeling offers a powerful approach for capturing the dynamic evolution of complex systems, particularly when dealing with latent variables that are not directly observable. In the context of analyzing time-evolving point clouds, this method allows us to model the underlying dynamics of topological features (e.g., persistence diagrams) without explicitly tracking individual point trajectories. This is particularly useful when dealing with high-dimensional or noisy data where precise tracking is difficult. A key advantage is the ability to learn a continuous representation of the evolution of topological features, leading to smoother and more robust predictions. The use of neural ODEs provides a flexible and differentiable framework that can be readily integrated into deep learning architectures. Training typically involves optimizing a loss function that balances the reconstruction of observed topological features with the smoothness of the latent ODE trajectory. The choice of the ODE solver impacts computational efficiency and numerical stability, demanding careful consideration. Stability results from persistent homology theory underpin the choice of this modeling approach, justifying the use of continuous latent variable models. Overall, latent ODE modeling emerges as an effective tool for characterizing the dynamics of latent structures in spatiotemporal data. This approach is particularly well-suited for scenarios involving collective behavior, where emergent global patterns are of interest rather than detailed individual motions.

PH Vectorization

#

Persistent Homology (PH) is a powerful topological data analysis technique, but its output—persistence diagrams—are not directly amenable to machine learning algorithms. PH vectorization addresses this by transforming persistence diagrams into vectors, enabling their use in various machine learning tasks. Several vectorization methods exist, each with its strengths and weaknesses. Some methods, like persistence images, focus on capturing the density of points in the diagram, while others, like persistence landscapes, use functions to represent the diagram’s features. The choice of vectorization method is crucial, as it impacts the stability and informativeness of the resulting vectors. A stable vectorization method ensures that small changes in the input persistence diagram result in small changes in the output vector, which is essential for robust machine learning applications. Careful consideration should be given to the choice of vectorization method based on the specific application and its sensitivity to noise and variations in the input data. Furthermore, the dimensionality of the resulting vector is an important hyperparameter that affects both computational cost and performance. Effective PH vectorization is a critical step in leveraging the power of PH for machine learning tasks related to time-evolving point cloud data.

Scalability & Stability

#

The paper’s approach demonstrates strong scalability and stability. Scalability is achieved by focusing on topological features instead of individual trajectories, allowing the method to handle a large number of entities. This avoids computationally expensive tracking, making it suitable for analyzing large-scale datasets. Stability is ensured through the use of persistent homology, a robust topological technique known for its stability with respect to noisy data and minor perturbations. The reliance on vectorized persistence diagrams further contributes to stability for downstream regression tasks. The use of recent theoretical results on the stability of persistence diagrams and their vectorizations provides a strong mathematical foundation supporting these claims. The choice of continuous latent variable models (like latent ODEs) provides a smooth and stable way to model the evolution of topological features over time. Experiments show that the model maintains accuracy even when observing a fraction of the total observation time, indicating robustness to missing data. The paper’s combination of these features addresses both scalability and stability concerns effectively.

Future Research

#

Future research directions stemming from this work on Neural Persistence Dynamics could explore several promising avenues. Extending the model to handle higher-dimensional data is crucial, as the current approach’s reliance on Vietoris-Rips complexes becomes computationally expensive with increasing dimensionality. Investigating alternative topological summaries, such as witness complexes or alpha complexes, could mitigate this limitation. Another key area is improving the scalability of the framework, particularly for large numbers of observation sequences. Exploring more efficient methods for learning latent ODEs and incorporating more sophisticated regression techniques would be beneficial. Furthermore, developing theoretically grounded stability results for the vectorized persistence diagrams would strengthen the model’s foundation. The current Lipschitz continuity property is a valuable first step, but tighter bounds would enhance the approach’s robustness. Finally, applying Neural Persistence Dynamics to diverse application domains beyond collective behavior, where topological features evolve over time, represents a significant opportunity. Examples include analyzing dynamic networks, tracking protein folding, or studying the evolution of ecosystems. These explorations could reveal new and valuable insights in many different scientific areas.

More visual insights

#

More on figures

This figure illustrates the overall workflow of the Neural Persistence Dynamics model. It starts with a time series of point clouds, which are then processed using persistent homology to extract topological features. These features are vectorized and input to a latent ODE, a type of neural network that models continuous changes over time. The model’s latent path is then used to predict parameters of a governing equation for collective behavior, such as flocking or swarming. The diagram highlights the steps involved, showing the transition from point clouds to persistence diagrams to vectorizations and finally to parameter prediction.

This figure shows the performance of the proposed method (Ours, v1) and the PSK method [23] on the dorsogna-10k dataset, varying the simulation time T from 2000 to 20000. The x-axis represents the maximum simulation time used to extract sequences of length 1000. The y-axis on the left shows the variance explained (VE), and the y-axis on the right shows the symmetric mean absolute percentage error (SMAPE). Error bars indicate the standard deviation over five random train/test splits. The results demonstrate that the proposed method is less sensitive to the increase of simulation time compared to the PSK method.

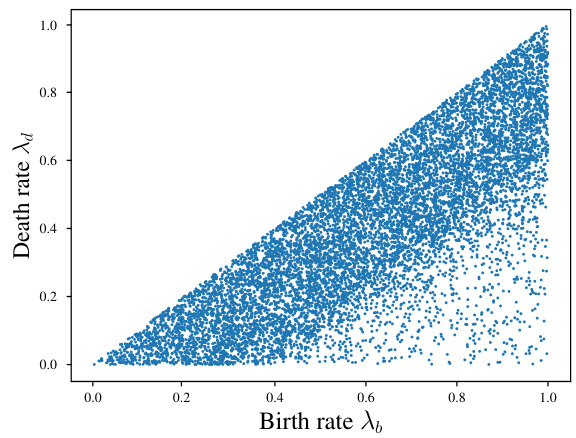
This figure shows the distribution of birth rates (λb) and death rates (λd) used to generate the volex-10k dataset. The x-axis represents the birth rate and the y-axis represents the death rate. Each point represents a single simulation run with a specific pair of birth and death rates. The distribution is concentrated in a triangular region, indicating a positive correlation between birth and death rates. This is expected since a higher birth rate is likely to result in a higher death rate for a population with a finite carrying capacity.

More on tables

This table compares the performance of the proposed Neural Persistence Dynamics model against two state-of-the-art methods (Path Signature Kernel and Crocker stacks) for parameter regression tasks on four different datasets simulating collective behavior. It highlights the superior performance of the proposed model across various metrics (VE and SMAPE), particularly when using a combination of topological and geometric features (joint model). The table also notes the varying number of parameters used in the different datasets and simulation settings for a fairer comparison.

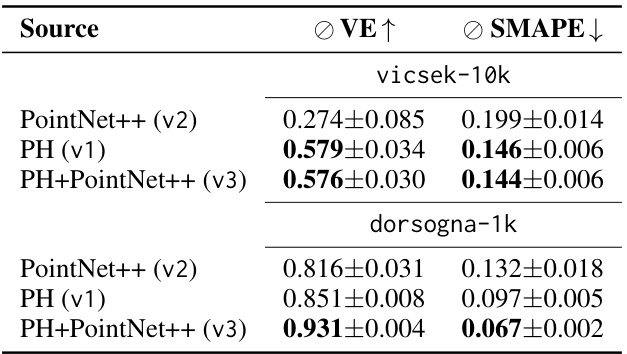
This table shows the variance explained (VE) and Symmetric Mean Absolute Percentage Error (SMAPE) for different model variants using various point cloud representations. Specifically, it compares using only PointNet++, only persistent homology (PH), and a combination of both. The results are presented for the vicsek-10k and dorsogna-1k datasets. The purpose is to demonstrate the complementary nature of PH and PointNet++ features when used together for improved parameter regression performance.

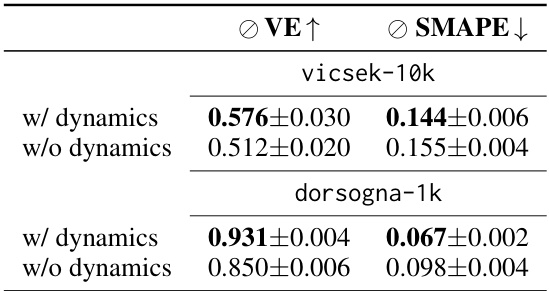
This table presents the ablation study comparing the performance of the model with and without explicit latent dynamics. The results are shown in terms of Variance Explained (VE) and Symmetric Mean Absolute Percentage Error (SMAPE) for two datasets: vicsek-10k and dorsogna-1k. Higher VE and lower SMAPE indicate better performance. The comparison highlights the benefit of incorporating latent dynamics for improved parameter regression accuracy.

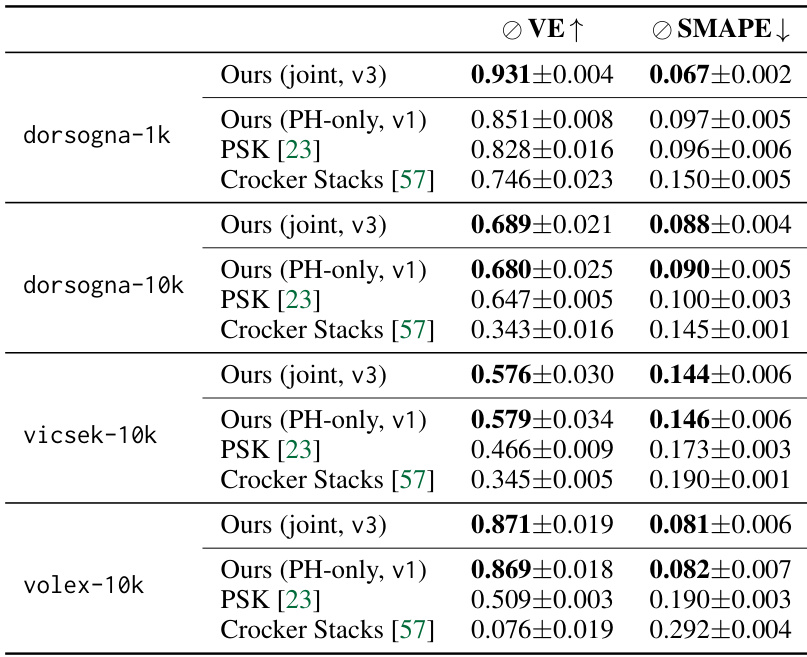
This table compares the performance of the proposed Neural Persistence Dynamics model against state-of-the-art methods (PSK and Crocker Stacks) on four different datasets simulating collective behavior. It shows the Variance Explained (VE) and Symmetric Mean Absolute Percentage Error (SMAPE) for parameter regression tasks. The results highlight the superior performance of the proposed model across all datasets and different parameter settings.

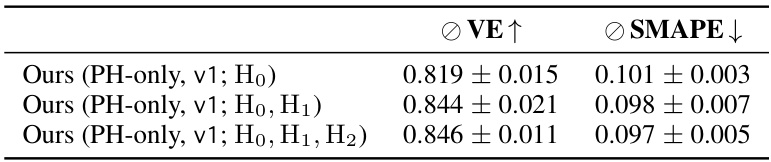
This table presents the ablation study results on the dorsogna-1k dataset to evaluate the impact of using different homology dimensions (H0, H1, and H2) in the proposed Neural Persistence Dynamics model. It compares the performance (VE and SMAPE) when only 0-dimensional features (H0), 0- and 1-dimensional features (H0, H1), and all three dimensions (H0, H1, H2) are used. The results show that including higher dimensional features does not significantly improve performance over the baseline using only H0.

This table compares the performance of the proposed Neural Persistence Dynamics method against two state-of-the-art approaches (PSK and Crocker stacks) on four different datasets of collective behavior. The table shows the variance explained (VE) and Symmetric Mean Absolute Percentage Error (SMAPE) for parameter regression tasks. Different model variants are included in the comparison. The results highlight the superior performance of the proposed method across various datasets and model parameters.

This table shows the results of an ablation study comparing different point cloud representations (PH and PointNet++) for parameter regression. It demonstrates the performance gains obtained when combining both representations versus using either one alone, highlighting the complementary nature of topological and geometric features in capturing collective behavior dynamics.

This table compares the performance of the proposed Neural Persistence Dynamics model against two state-of-the-art methods (PSK and Crocker Stacks) for parameter regression tasks on four different datasets simulating collective behavior. It shows the variance explained (VE) and Symmetric Mean Absolute Percentage Error (SMAPE) for each method and dataset, highlighting the superior performance of the proposed model. Different variants of the model are also compared to analyze the impact of specific model components.

This table compares the performance of the proposed Neural Persistence Dynamics model against two state-of-the-art methods (PSK and Crocker stacks) for parameter regression tasks on four different datasets of collective behavior. The table shows the variance explained (VE) and symmetric mean absolute percentage error (SMAPE) for each method and dataset, highlighting the superior performance of the proposed model. The table also notes that the dorsogna-1k dataset is a replication of a previous study’s setup, using only two parameters. In contrast, the dorsogna-10k, vicsek-10k and volex-10k datasets all use four parameters.

Full paper

#