↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large Language Models (LLMs) are computationally expensive due to their massive number of parameters. Existing pruning methods often apply uniform sparsity across all layers, hindering performance. This paper addresses the limitations of these methods, which fail to allocate adaptive layer-wise sparsities. The challenge lies in finding the optimal balance between compression and preserving model accuracy.
The paper proposes DSA, an automated framework that discovers optimal sparsity allocation strategies. DSA uses an evolutionary algorithm to explore various combinations of pre-processing, reduction, transform, and post-processing operations, aiming for the best balance between compression and accuracy. Experiments show DSA significantly improves performance across multiple LLMs and diverse tasks compared to existing methods, even at high sparsity levels. This approach provides a systematic and automated solution to a critical problem in LLM optimization.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on LLM compression and optimization. It introduces a novel automated framework for discovering optimal sparsity allocation schemes for layer-wise pruning, leading to significant performance improvements and opening new avenues for efficient LLM deployment.
Visual Insights#

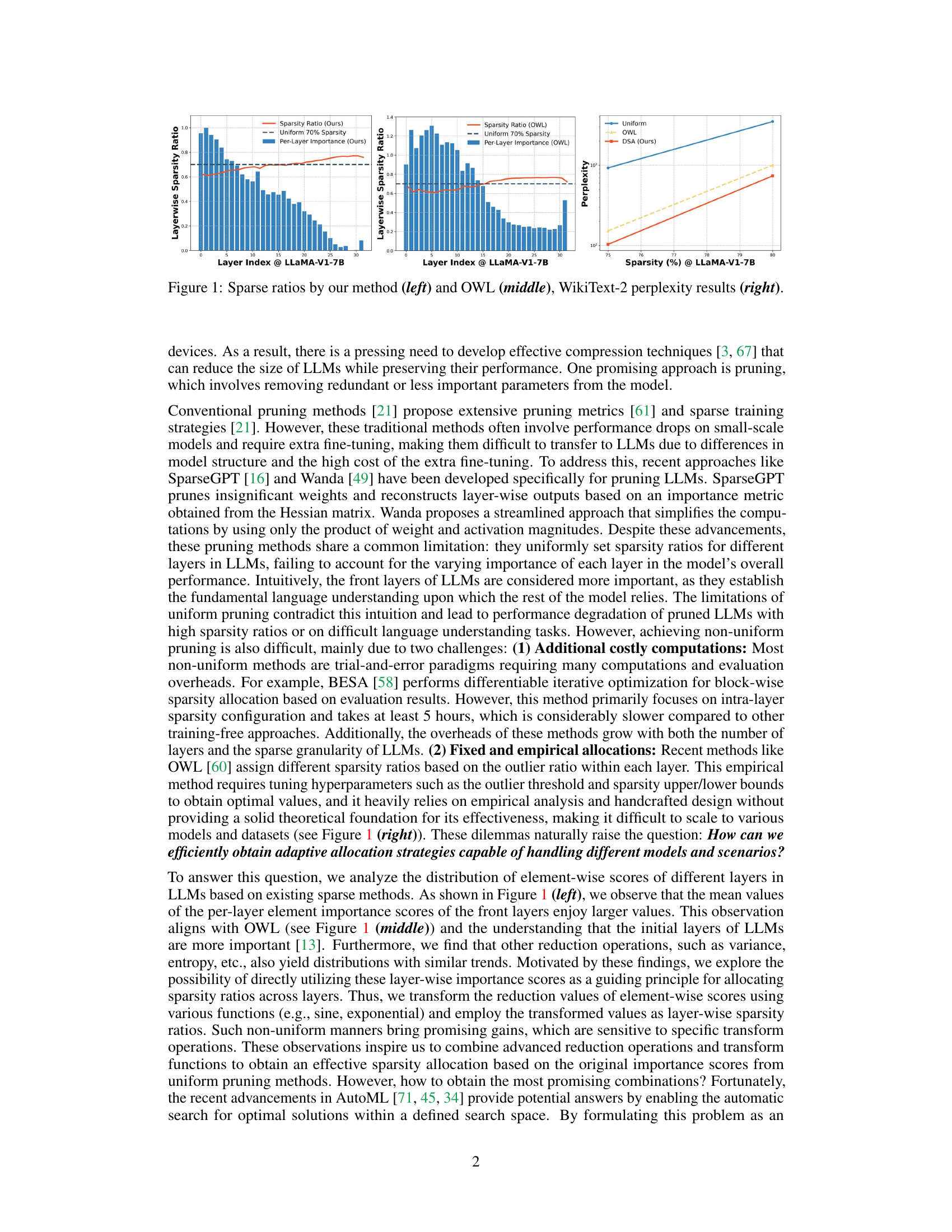
This figure compares the layer-wise sparsity ratios achieved by the proposed DSA method and the OWL method, along with a uniform sparsity baseline. The left and middle panels show the sparsity ratios assigned to each layer of a LLaMA-V1-7B model by DSA and OWL, respectively. The right panel shows the perplexity on WikiText-2 dataset for LLaMA-V1-7B model under the different sparsity methods. It visually demonstrates how the proposed method dynamically allocates sparsity based on layer importance, leading to better performance compared to the uniform sparsity and OWL approaches.

This table lists a subset of the operations used in the search space of the DSA framework. It shows the operation ID, name, and mathematical expression for each operation. These operations are categorized into pre-processing, reduction, transformation, and post-processing steps, which are combined to create allocation functions that map element-wise scores to sparsity ratios in LLMs.
In-depth insights#
Adaptive Sparsity#
Adaptive sparsity, in the context of large language model (LLM) compression, signifies techniques that dynamically adjust sparsity levels across different layers or components of the model. Unlike uniform sparsity methods that apply a fixed sparsity ratio across all parts, adaptive approaches leverage metrics, often related to layer-wise importance or sensitivity analysis, to determine the optimal sparsity allocation. This data-driven approach aims to maximize compression while minimizing performance degradation. Key advantages include the ability to preserve crucial information in more important layers, allowing for higher overall compression rates compared to uniform methods. However, challenges include the computational cost of determining the optimal sparsity allocation, and the potential for these methods to be sensitive to the specific dataset and model architecture used. The ultimate effectiveness hinges on accurately identifying and quantifying the contribution of each component in an LLM, a complex task that necessitates robust and principled methodologies.
Evolutionary Search#
The evolutionary search strategy employed in this research is a sophisticated approach to optimizing the allocation of sparsity in large language models. Instead of relying on manual design or exhaustive grid search, it leverages the power of evolutionary algorithms. A population of diverse allocation functions is initially generated, each representing a potential strategy for distributing sparsity across layers. These functions are then evaluated based on their performance on a validation set, with the best-performing functions selected for the next generation. Crossover and mutation operations are used to create new candidate functions, encouraging exploration of the search space while preserving desirable traits from successful parents. This iterative process continues until a satisfactory allocation function is identified. This approach offers the significant advantage of automating a complex optimization problem, potentially leading to more effective and efficient sparsity allocation strategies than traditional methods. The use of an evolutionary algorithm ensures the robustness of the process, as it avoids the risk of getting stuck in local optima.
LLM Compression#
LLM compression techniques are crucial due to the high computational cost and memory footprint of large language models. Pruning, a common method, focuses on removing less important parameters. However, existing methods often use uniform sparsity, ignoring the varying importance of different layers. Adaptive layer-wise sparsity allocation is a more effective approach, but it presents a significant challenge due to the need for computationally expensive and manual optimizations. Automated frameworks are needed to efficiently search for optimal sparsity allocation strategies, effectively combining element-wise pruning metrics with per-layer importance scores to define layer-wise sparsity ratios. Evolutionary algorithms can provide a solution to efficiently search the potentially vast space of possible functions, resulting in significant compression with minimal performance degradation. Future work should focus on developing more robust and efficient search algorithms and exploring the potential synergy with other compression techniques like quantization.
Zero-Shot Gains#
Zero-shot gains in large language models (LLMs) represent a significant advancement, showcasing the models’ ability to generalize to unseen tasks without explicit training. These gains highlight the power of transfer learning and the inherent knowledge encoded within the vast parameter space of LLMs. Analyzing these gains requires careful consideration of the evaluation benchmarks and metrics employed; a model exhibiting strong zero-shot performance on one task might underperform on another. The magnitude of zero-shot gains is often correlated with model size and pre-training data, suggesting that scaling up models can lead to more robust generalization. However, simply scaling up models is not sufficient to guarantee high zero-shot performance, as other factors such as architecture and training methodology play a critical role. Therefore, research into effective zero-shot learning techniques within LLMs remains an active area of study, with the potential to unlock even greater capabilities for these powerful models. Further research could focus on optimizing model architectures, exploring novel training methods, and developing more comprehensive evaluation strategies to fully understand and harness the potential of zero-shot learning.
Future of DSA#
The future of DSA (Discovering Sparsity Allocation) in LLM pruning hinges on several key advancements. Further research into automated search space optimization is crucial; exploring more sophisticated search algorithms beyond evolutionary methods could significantly accelerate the discovery of optimal sparsity allocation functions. Expanding the search space itself to incorporate additional pre-processing, reduction, and transformation techniques, including potentially more advanced neural network-based approaches, is needed to capture increasingly complex relationships within LLMs. Improving the theoretical understanding of why certain allocation strategies perform better than others would provide a solid foundation for more targeted function discovery, thereby reducing reliance on computationally expensive search procedures. Finally, assessing DSA’s adaptability to various LLM architectures and downstream tasks is critical. Thorough evaluation across diverse models and applications is needed to establish its generality and potential for widespread adoption. Ultimately, the future of DSA will depend on its ability to deliver robust and efficient pruning across the rapidly evolving landscape of large language models.
More visual insights#
More on figures
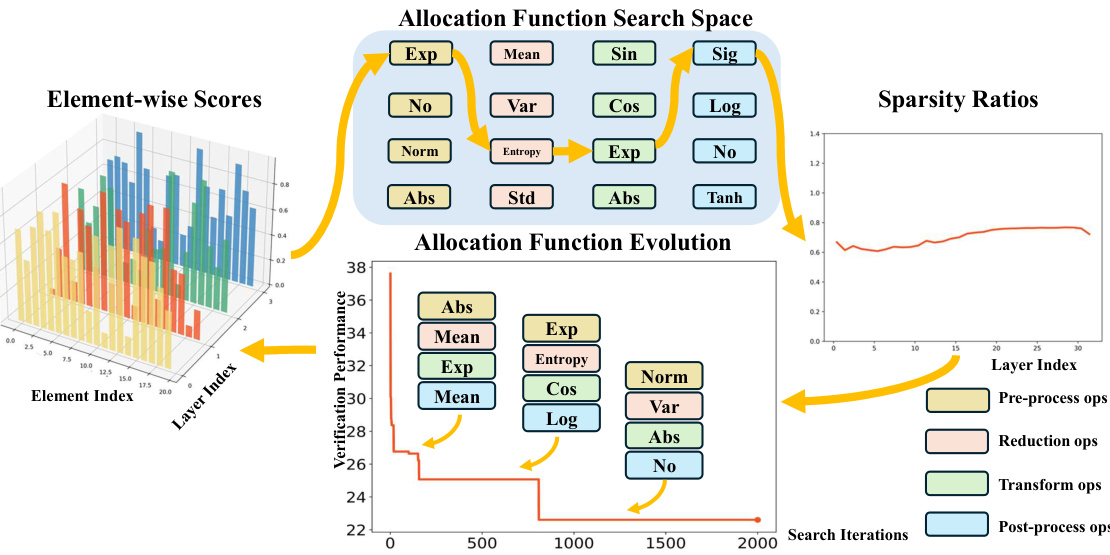
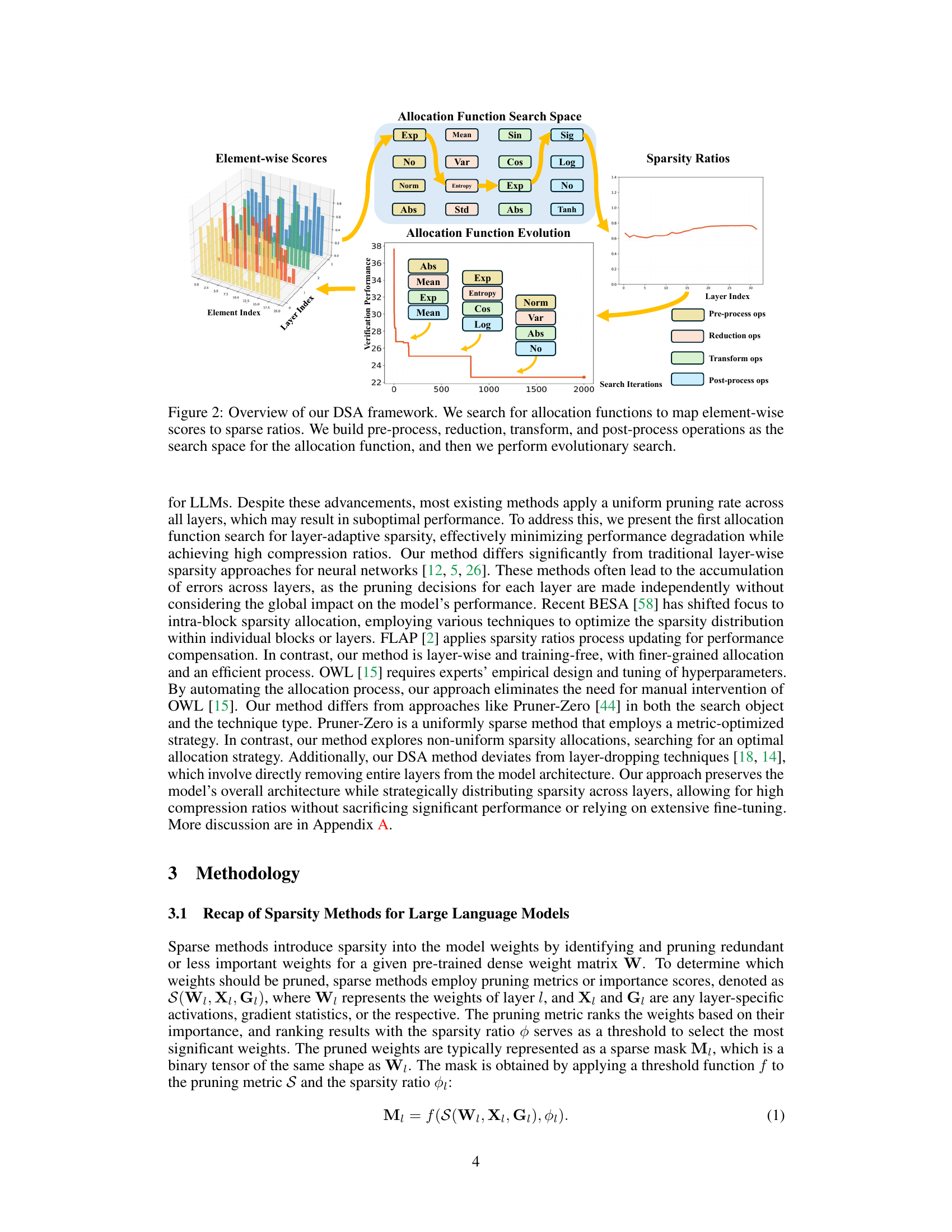
This figure illustrates the DSA (Discovering Sparsity Allocation) framework for finding optimal sparsity allocation functions in LLMs. It shows a workflow that begins with element-wise scores, proceeds through four stages of operations (pre-processing, reduction, transformation, and post-processing), and ultimately arrives at sparsity ratios. The evolutionary search process, depicted as a graph of verification performance against search iterations, is also shown. The operations within each stage are depicted with boxes indicating their role and contribution to the overall process.
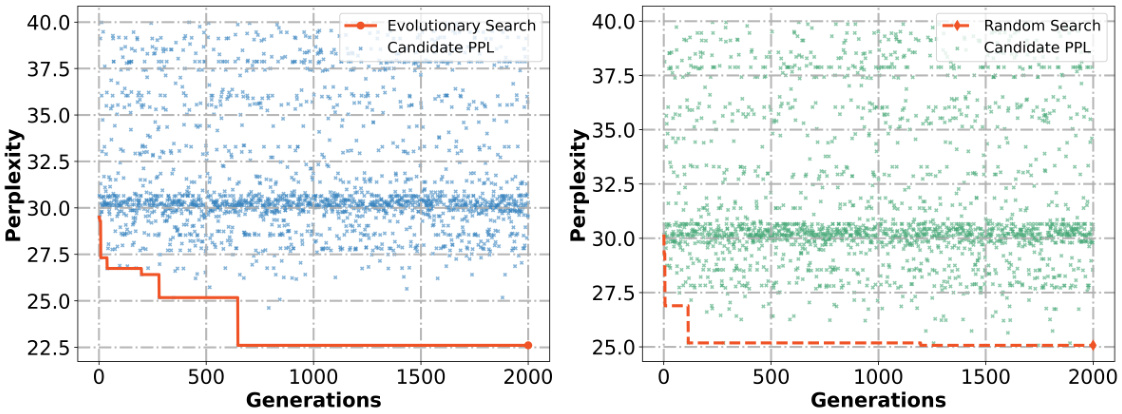
This figure compares the performance of two search algorithms, evolutionary search and random search, in finding optimal sparsity allocation functions for the LLaMA-1 7B language model on the WikiText-2 dataset. The x-axis represents the number of generations in the search, and the y-axis shows the perplexity, a measure of the model’s performance (lower is better). The plot shows that evolutionary search converges to a lower perplexity significantly faster than random search, indicating its greater efficiency in finding high-performing allocation functions.
More on tables
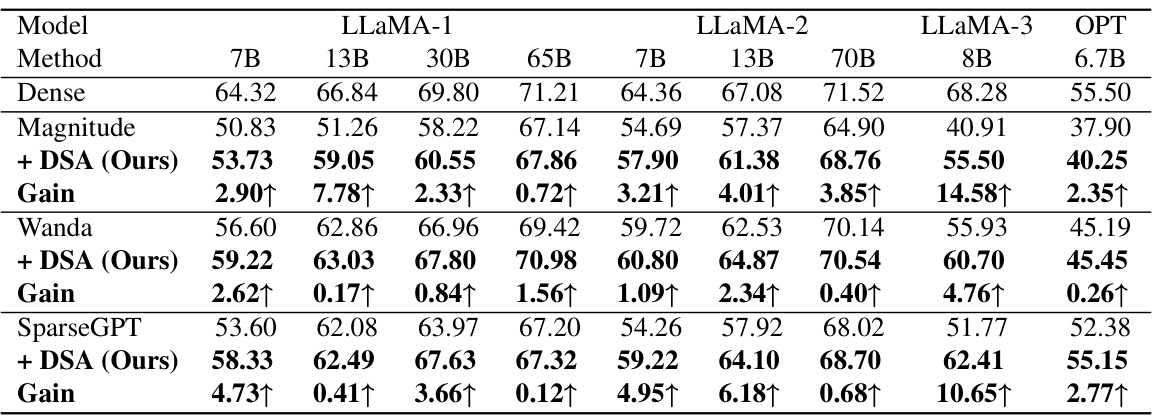
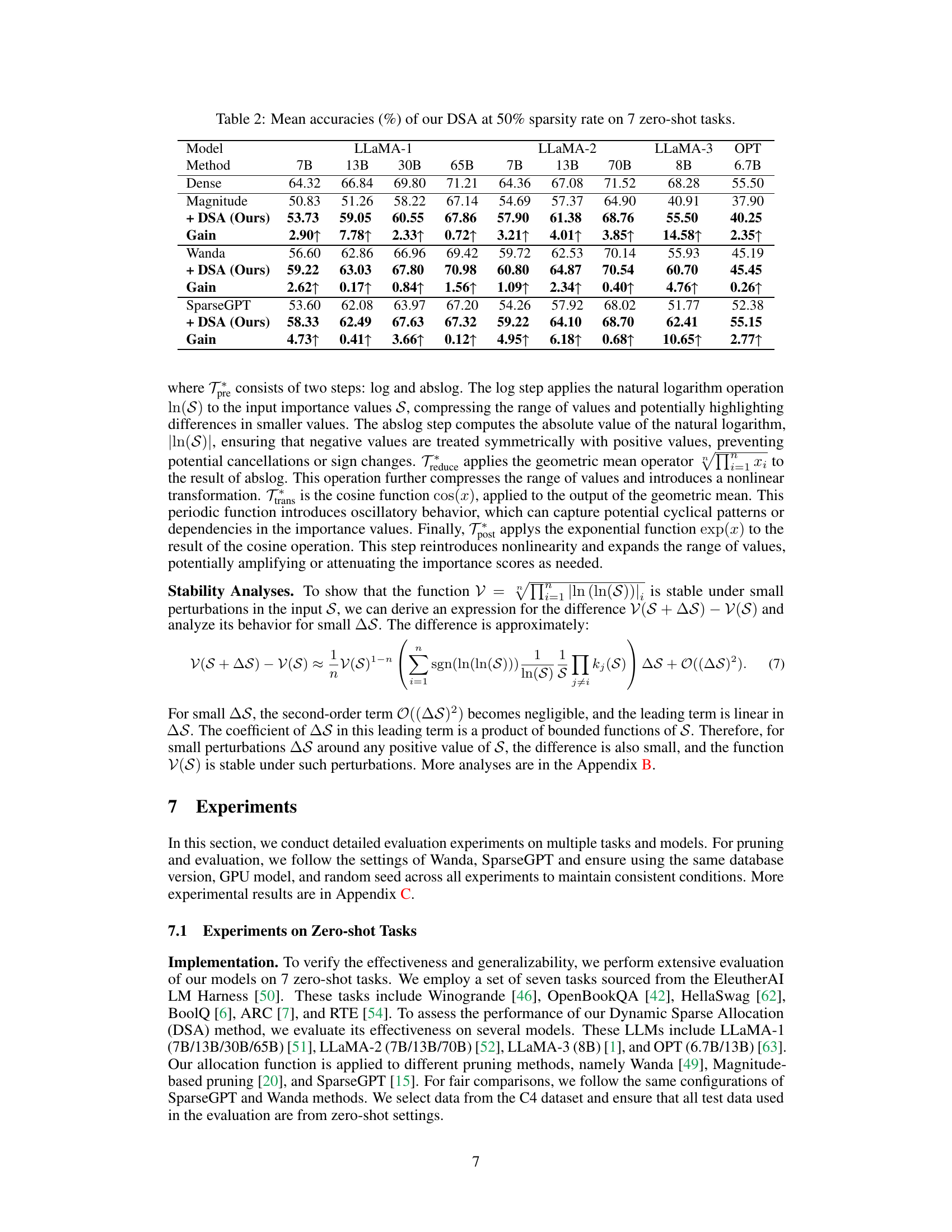
This table presents the mean accuracy results achieved by the proposed DSA method on seven zero-shot tasks. The results are shown for several large language models (LLMs) including LLaMA-1, LLaMA-2, LLaMA-3 and OPT at 50% sparsity. The performance of DSA is compared to baseline methods (Magnitude, Wanda, and SparseGPT) to highlight its improvements.
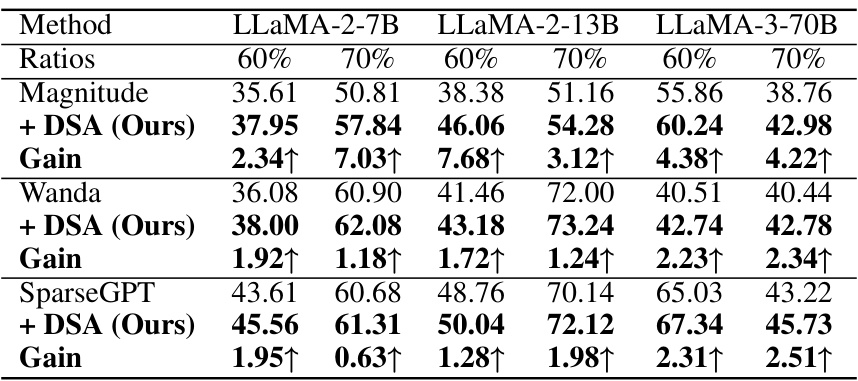
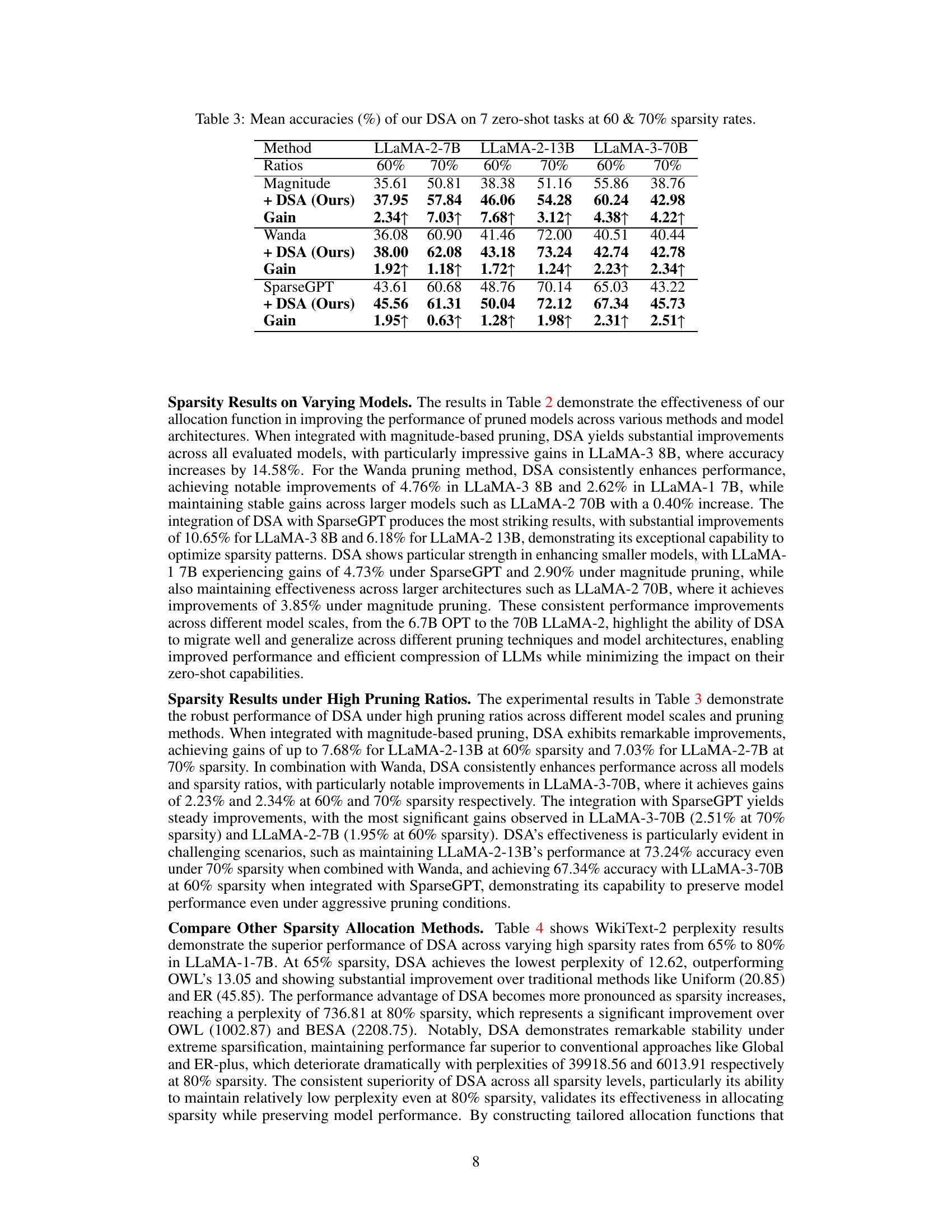
This table presents the mean accuracies achieved by the DSA method on seven zero-shot tasks. The results are shown for different LLMs (LLaMA-2-7B, LLaMA-2-13B, LLaMA-3-70B) at two different sparsity rates (60% and 70%). Comparisons are provided against three baseline methods: Magnitude pruning, Wanda, and SparseGPT, highlighting the performance improvement achieved by integrating DSA with each of these methods. The ‘Gain’ row indicates the improvement in accuracy achieved by using DSA in comparison to the respective baseline method.

This table presents the WikiText-2 perplexity results for different sparsity allocation methods applied to the LLaMA-1-7B model at high sparsity ratios (65% to 80%). The methods compared are Global, ER-plus, ER, Uniform, BESA, OWL, and the proposed DSA method. Lower perplexity indicates better performance. The table showcases DSA’s superior performance, especially at higher sparsity rates, demonstrating its ability to effectively allocate sparsity across layers.

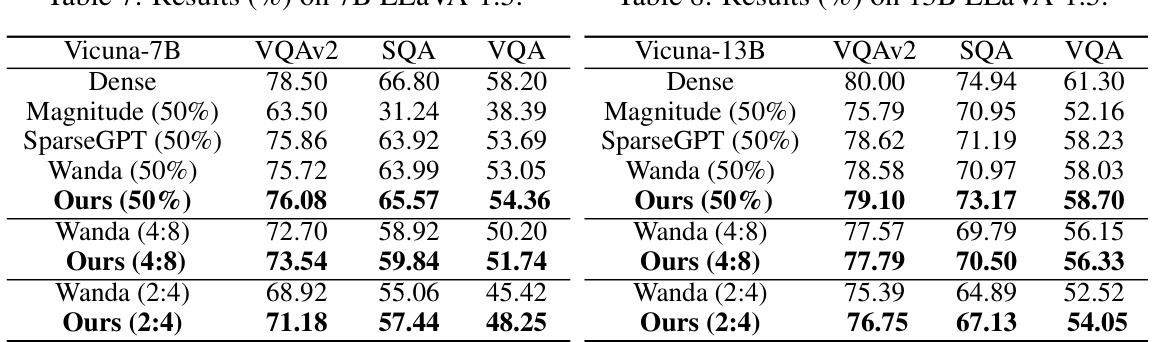
This table presents the results of the experiments conducted on the 7B LLaVA-1.5 model. It shows the performance of different methods (Dense, Magnitude, SparseGPT, Wanda, and the proposed method ‘Ours’) on various multimodal tasks (VQAv2, SQA, VQA). The results are presented as percentages, indicating the accuracy or performance achieved by each method on each task. This table highlights the improvements achieved by the proposed method compared to existing methods in multimodal tasks.
This table presents the mean accuracies achieved by the proposed DSA method on seven zero-shot tasks, using different large language models (LLMs) at a 50% sparsity rate. It compares the performance of DSA against baseline methods (Magnitude, Wanda, and SparseGPT) to demonstrate the improvement in accuracy obtained by incorporating DSA’s adaptive sparsity allocation. The results show the accuracy gain for each LLM and method.

This table compares the characteristics of the proposed DSA method and the baseline Pruner-Zero method. The comparison covers the types of sparsity (uniform vs. non-uniform), the task addressed (symbolic pruning metric), the search space used to find the optimal sparsity allocation, the input and output data used in the allocation function, and the strategy used to obtain the sparsity allocation (symbolic regression vs. evolutionary algorithm). It highlights the key differences in the approaches taken by DSA and Pruner-Zero in achieving sparsity.

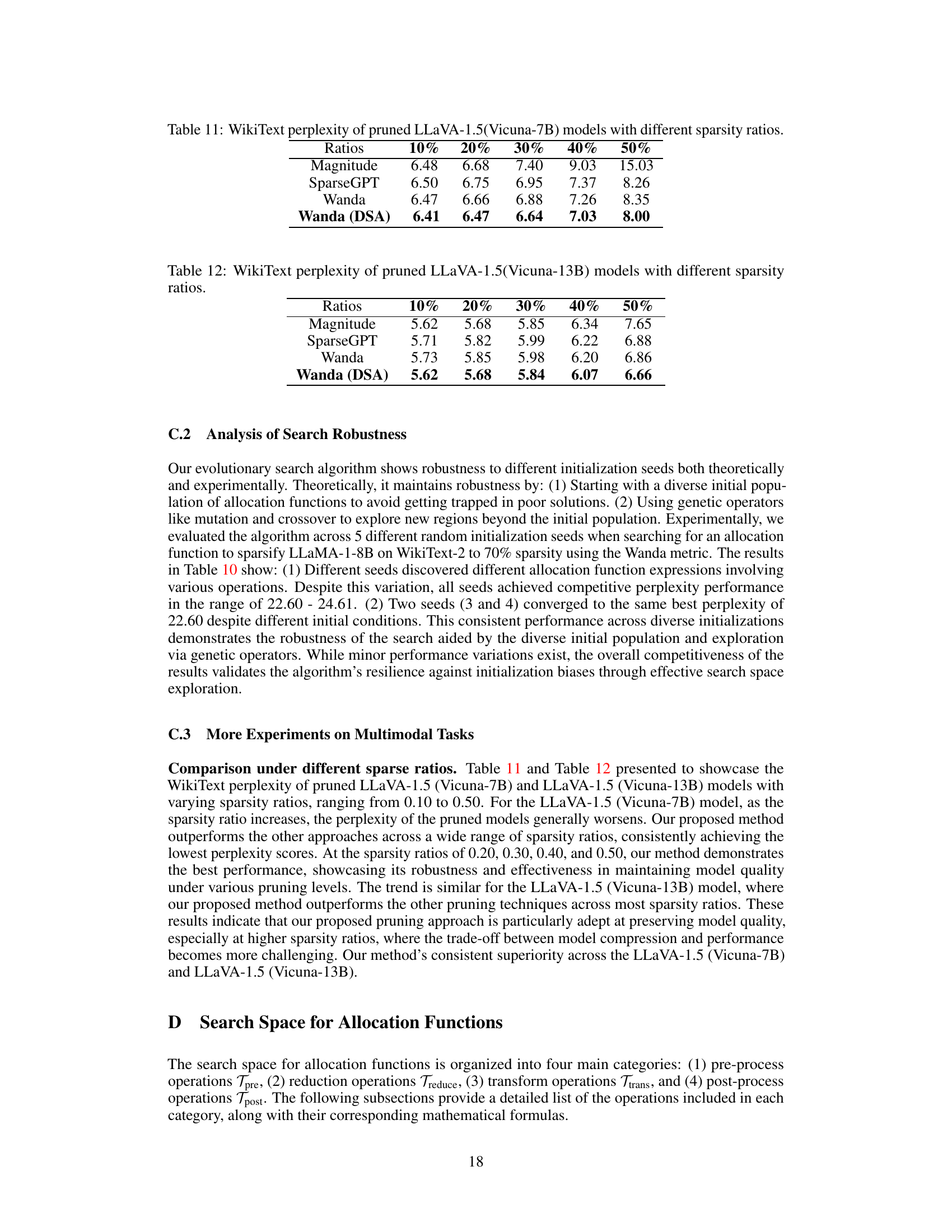
This table presents the WikiText-2 perplexity results obtained using the best allocation functions found through evolutionary search with five different random initial seeds. The experiments used the Wanda metric and a 70% sparsity level on the LLaMA-1-8B model. The table demonstrates the robustness of the evolutionary search, as similar perplexity scores were achieved across different initializations despite resulting in distinct allocation functions.
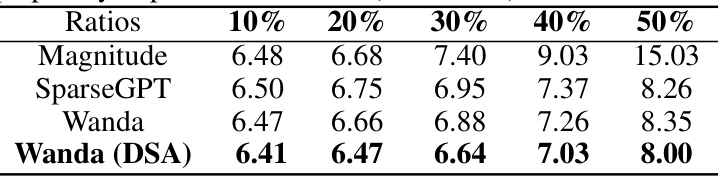
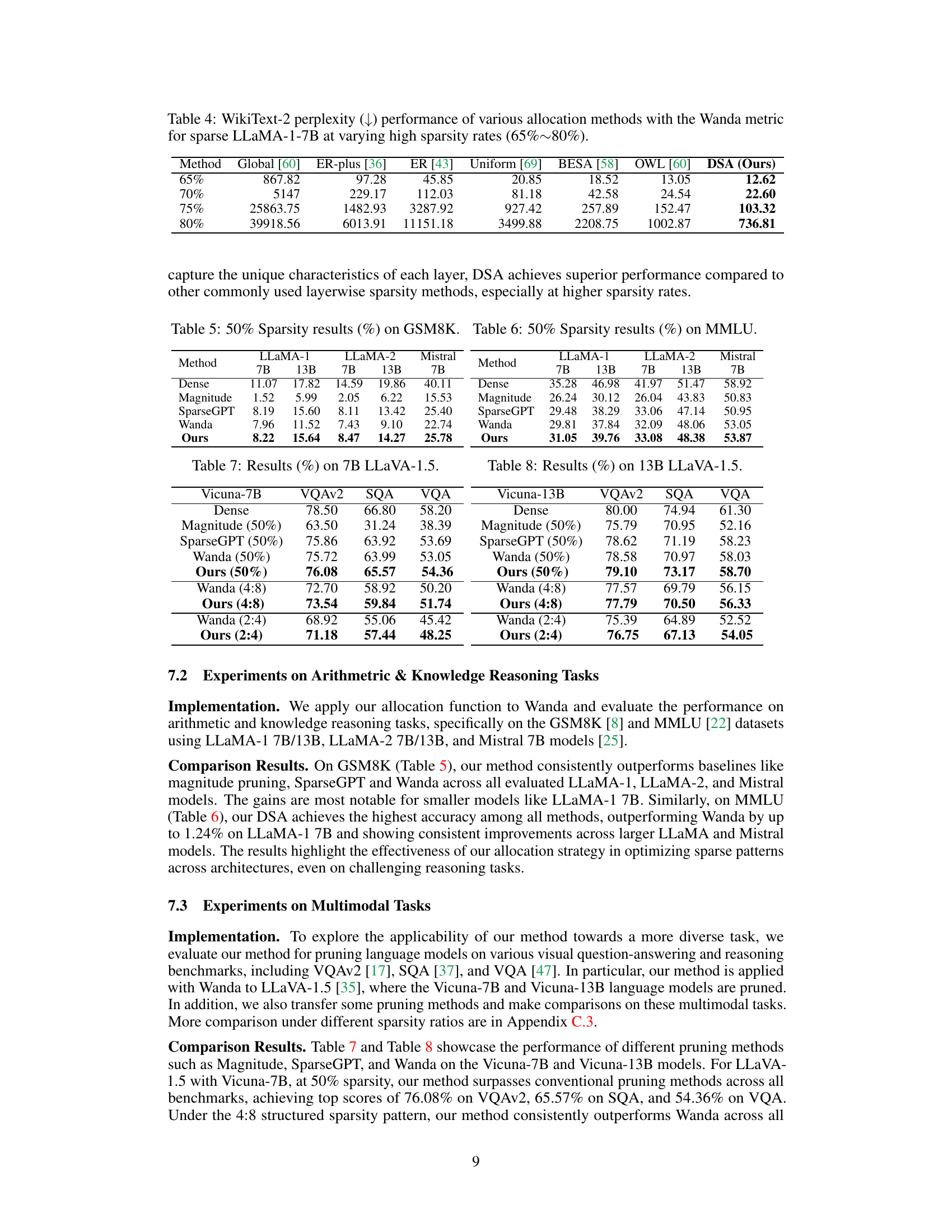
This table displays the WikiText perplexity scores achieved by different pruning methods (Magnitude, SparseGPT, Wanda) and the proposed DSA method integrated with Wanda on the LLaVA-1.5 model using Vicuna-7B at various sparsity levels (10%, 20%, 30%, 40%, 50%). Lower perplexity indicates better performance. The results demonstrate the impact of the proposed DSA method in improving the model’s performance under varying sparsity conditions.

This table shows the WikiText perplexity results for different sparsity ratios (10%, 20%, 30%, 40%, 50%) when using four different pruning methods: Magnitude, SparseGPT, Wanda, and Wanda with DSA. It demonstrates the performance of the pruning methods on the Vicuna-13B model within the LLaVA-1.5 framework. The values indicate the model’s perplexity, a measure of how well the model predicts the next word in a sequence. Lower perplexity scores indicate better performance.
Full paper#