↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large graphs are computationally expensive to process using GNNs. Graph coarsening, a technique to reduce graph size, is often employed to address this issue. However, existing coarsening methods lack theoretical guarantees when performing message-passing on the coarsened graph, potentially leading to inaccurate results. This paper addresses this issue by proposing a novel message-passing operation tailored to coarsened graphs. This operation offers theoretical guarantees on preserving the propagated signal during message-passing.
The paper’s main contribution is a new message-passing matrix (SMP) specifically designed for coarsened graphs. This matrix ensures theoretical guarantees on the preservation of propagated signals, translating spectral properties of the Laplacian to message-passing guarantees, even when the original graph is undirected. The proposed method is validated through node classification tasks on synthetic and real-world datasets, demonstrating improved results compared to existing methods and highlighting the practical value of the novel approach.
Key Takeaways#
Why does it matter?#
This paper is important because it bridges the gap between graph coarsening and Graph Neural Networks (GNNs). It provides theoretical guarantees for message-passing on coarsened graphs, a critical step for improving GNN efficiency and scalability, opening avenues for developing more efficient and reliable GNN training methods. This is particularly relevant given the increasing prevalence of large-scale graph data in various applications. The work also introduces a novel propagation matrix with improved performance compared to existing methods, offering practical improvements for researchers working with GNNs.
Visual Insights#

This figure shows an example of a uniform graph coarsening. (a) shows the original graph G. (b) shows the coarsened adjacency matrix Ac which represents the connections between the supernodes in the coarsened graph. (c) illustrates the proposed SMP (Specific Message-Passing matrix) for the case when S = A (adjacency matrix), highlighting the orientation of message passing even when the original graph is undirected. (d) displays the coarsening matrix Q, its pseudo-inverse Q+, and the projection matrix I = Q+Q, demonstrating the mathematical relationships involved in the coarsening process.
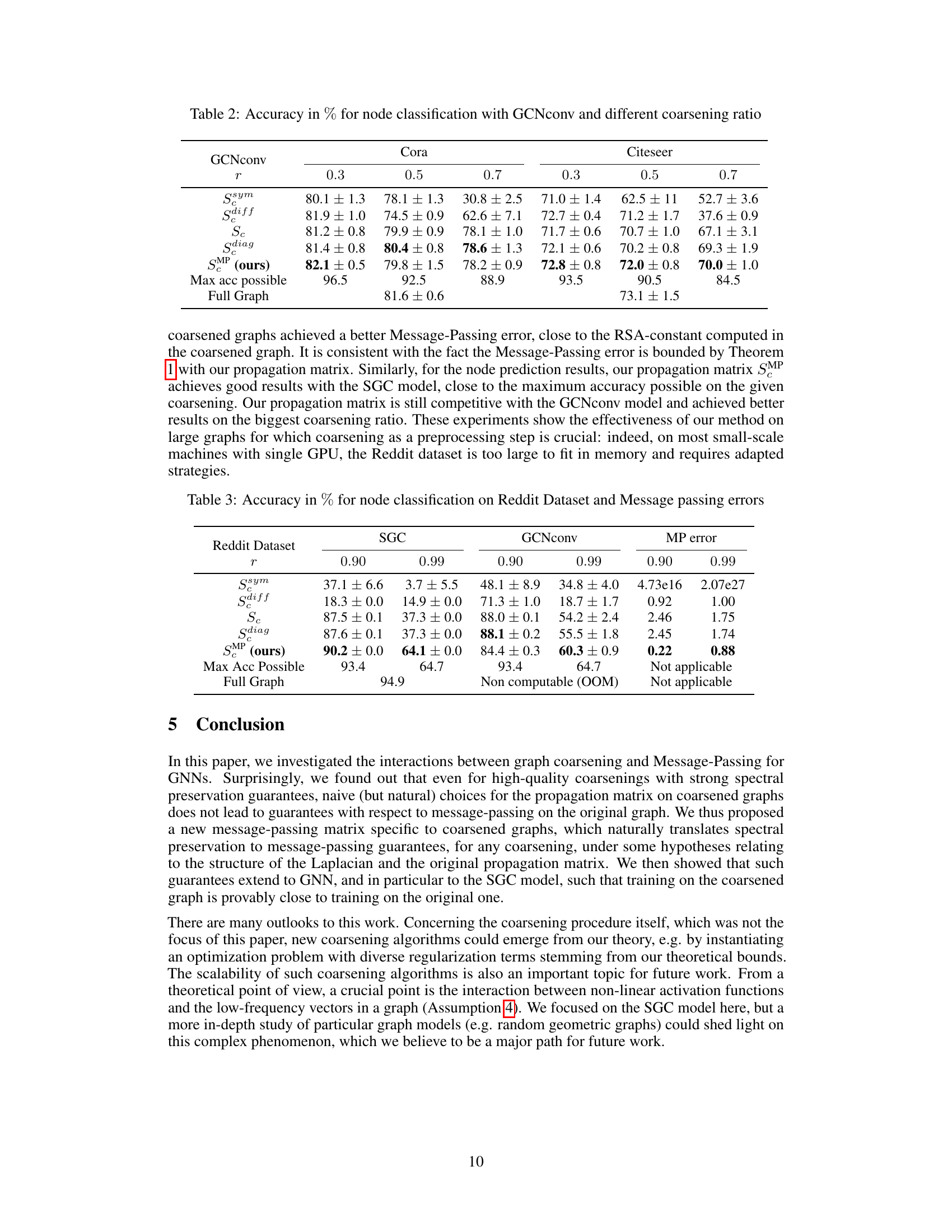
This table presents the accuracy (in percentage) of node classification using Simplified Graph Convolution (SGC) neural networks. The results are broken down by different coarsening ratios (0.3, 0.5, 0.7), showing the performance of various propagation matrices (SMP, Sc, Sdiag, etc.) on the Cora and Citeseer datasets. The ‘Max acc possible’ row indicates the maximum achievable accuracy given the coarsening, and ‘Full Graph’ shows the accuracy when using the entire graph without coarsening. The table highlights the improved accuracy achieved using the proposed SMP propagation matrix, especially at higher coarsening ratios.
In-depth insights#
Coarsening Guarantees#
The concept of “Coarsening Guarantees” in graph neural networks (GNNs) centers on maintaining crucial graph properties during the graph coarsening process. This is critical because GNNs rely heavily on graph structure, and simplifying a graph by reducing its size (coarsening) can lead to significant performance improvements in terms of computational efficiency and memory usage. However, naive coarsening can distort important structural information, negatively impacting GNN performance. Therefore, research focuses on developing coarsening methods that provide theoretical guarantees on preserving specific graph properties, such as spectral properties or the propagation of signals. These guarantees ensure that the coarsened graph remains a faithful representation of the original, allowing GNNs trained on the smaller graph to generalize well to the original, larger graph. The challenge lies in finding a balance: creating a significantly smaller graph while retaining enough structural information for effective GNN performance. Strong theoretical bounds are crucial for establishing confidence in the coarsening process, especially in scenarios where data is limited or computational resources are constrained.
Novel Propagation#
The concept of “Novel Propagation” in the context of graph neural networks (GNNs) and graph coarsening is intriguing. It suggests a new method for propagating information across a simplified graph structure (coarsened graph), aiming to improve the efficiency and accuracy of GNNs. This likely involves a new type of matrix operation or algorithm that differs from traditional message-passing schemes. The novelty probably lies in how it handles the information loss inherent in coarsening while preserving crucial structural or spectral properties. It might introduce oriented message passing, even on initially undirected graphs, potentially enhancing the ability to capture directional relationships. A key aspect of any “novel propagation” would be the demonstration of theoretical guarantees—proving that this method maintains a close approximation of the original, uncoarsened graph’s signal propagation. This theoretical grounding would be essential for establishing its reliability and superiority over naive message passing on a coarsened graph. The practical impact would be demonstrated through experiments showcasing improved performance on node classification tasks, potentially achieving better accuracy or faster training times compared to conventional methods. The efficiency gain from using a smaller coarsened graph is crucial, particularly for large-scale graph data. Overall, a successful “Novel Propagation” method would mark a significant advancement in GNN-based graph analysis.
Empirical Validation#
An Empirical Validation section would critically assess the proposed graph coarsening method with message-passing guarantees. It would involve experiments on diverse datasets, comparing the method’s performance against existing baselines using relevant metrics such as classification accuracy and computational efficiency. A key aspect would be demonstrating the method’s robustness to variations in graph structure and size. The results should showcase the improved performance of the proposed technique in preserving signal propagation compared to naive message-passing approaches on coarsened graphs, potentially corroborating the theoretical guarantees. Attention should be given to the choice of evaluation metrics, ensuring they directly reflect the core contribution of the research. The experimental setup and parameters should be detailed, facilitating reproducibility. Finally, a thorough analysis of the results should be performed, discussing potential limitations and suggesting directions for future research, particularly focusing on scalability and the applicability to larger and more complex graphs.
Limitations & Future#
The research paper’s core contribution is a novel message-passing scheme for graph coarsening, offering theoretical guarantees. A primary limitation is the focus on the Simplified Graph Convolution (SGC) model, which, while analytically convenient, may not fully capture the complexities of real-world GNN architectures. The assumptions around the Laplacian and the signal subspace (R) need further investigation to broaden the applicability of the theoretical guarantees. Computational cost is another limitation, particularly with the greedy coarsening algorithm, making it less suitable for extremely large graphs. Future work could involve extending the theoretical framework to handle more sophisticated GNNs, exploring alternative coarsening algorithms that are more scalable, and performing more extensive empirical evaluation on diverse and massive datasets. Investigating the influence of various Laplacian choices and the impact of non-uniform coarsenings would also significantly enhance the results.
Related Work#
The ‘Related Work’ section would ideally provide a thorough analysis of existing graph coarsening and graph neural network (GNN) literature. It should highlight the key differences between the proposed approach and prior methods, particularly concerning the handling of spectral properties and message-passing guarantees. A strong ‘Related Work’ section would critically evaluate existing graph reduction techniques (sampling, sparsification, distillation), comparing their strengths and weaknesses concerning efficiency, accuracy, and theoretical guarantees. It should emphasize the novelty of the proposed message-passing operation on coarsened graphs, especially regarding its oriented nature even for undirected graphs. Finally, it should place the work in context, demonstrating how the proposed approach addresses limitations in existing GNN training methods for large-scale graphs.
More visual insights#
More on figures

This figure shows the message-passing error for different propagation matrices (SMP, Sc, Sdiag, Sdiff, Ssym) against the coarsening ratio (r). The error is calculated as the L2 norm of the difference between the message-passing on the original graph and the lifted message-passing on the coarsened graph. The plot demonstrates that the proposed SMP matrix consistently outperforms other methods in minimizing this error, especially at higher coarsening ratios. The upper bound (CEL,Q,R) derived from Theorem 1 is also plotted, showing a positive correlation with the error of SMP.

This figure illustrates an example of uniform graph coarsening. Panel (a) shows the original graph G. Panel (b) displays the coarsened adjacency matrix Ac, representing the connections in the coarsened graph. Panel (c) depicts the proposed SMP (Specific Message Passing matrix) when the propagation matrix S is equal to the adjacency matrix A. Finally, Panel (d) shows the coarsening matrix Q, its pseudo-inverse Q+, and the projection operator I = Q+Q. This figure is essential to understanding the mathematical concepts behind graph coarsening and the construction of the new proposed propagation matrix.
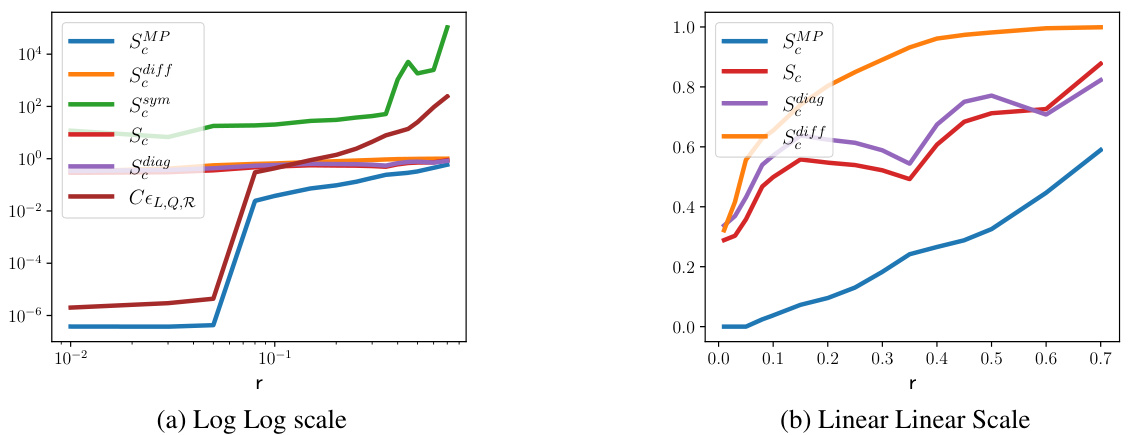
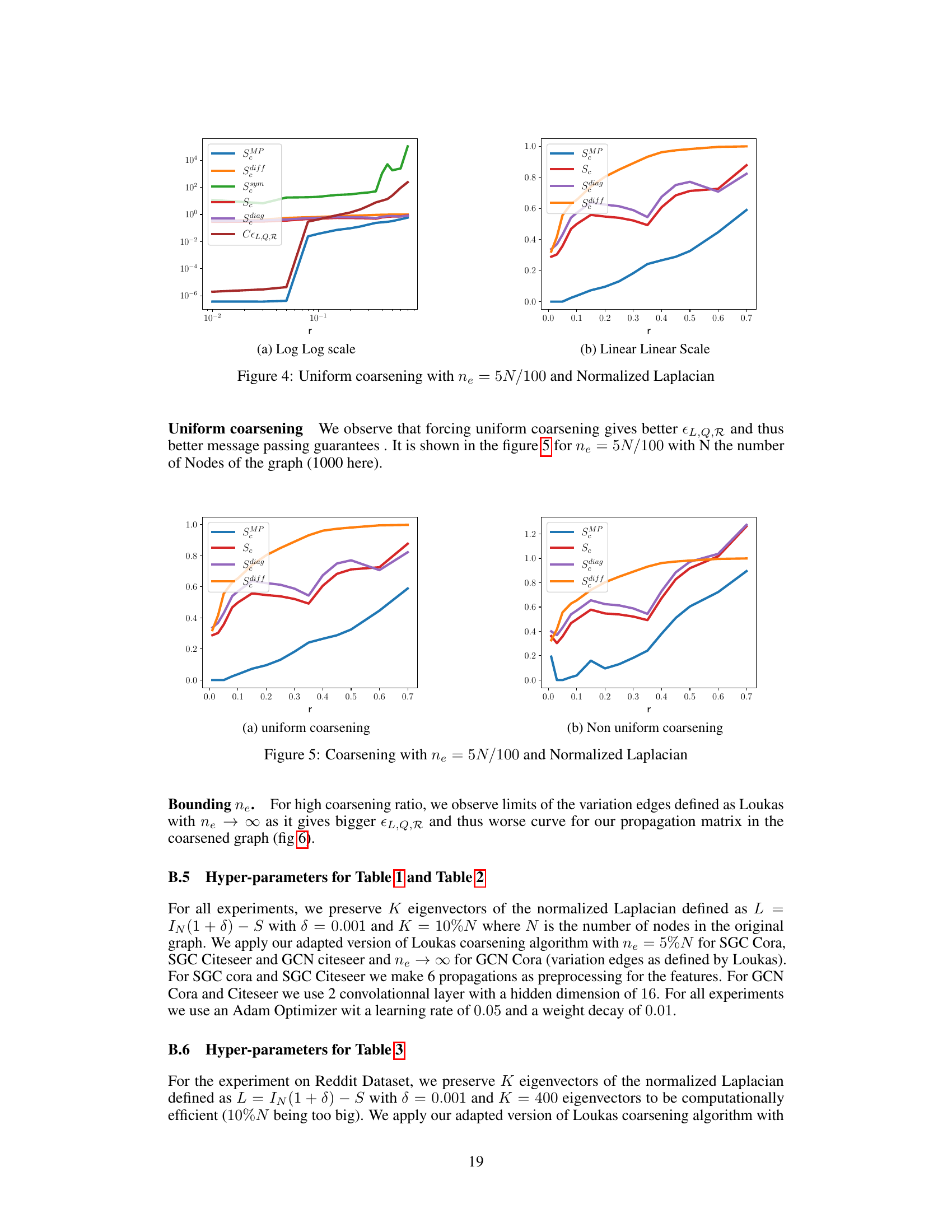
This figure compares the message-passing error for different propagation matrices on uniformly coarsened graphs with a normalized Laplacian. The x-axis represents the coarsening ratio (r), and the y-axis represents the message-passing error. The plot shows that the proposed propagation matrix (SMP) has significantly lower error compared to other choices, especially for higher coarsening ratios. The figure includes two subplots: (a) Log-Log scale and (b) Linear-Linear scale, to better visualize the behavior at different coarsening ratios.

This figure shows the Message-Passing error for different propagation matrices (SMP, Sc, Sdiag, Sdiff, Sym) as a function of the coarsening ratio (r). The error is measured as ||Skx - Q+(SMP)kxc||L for various signals x, with Np = 6 message-passing steps. The figure illustrates the effectiveness of the proposed propagation matrix SMP in preserving message-passing guarantees compared to other methods, demonstrating that the error is correlated with the RSA constant.
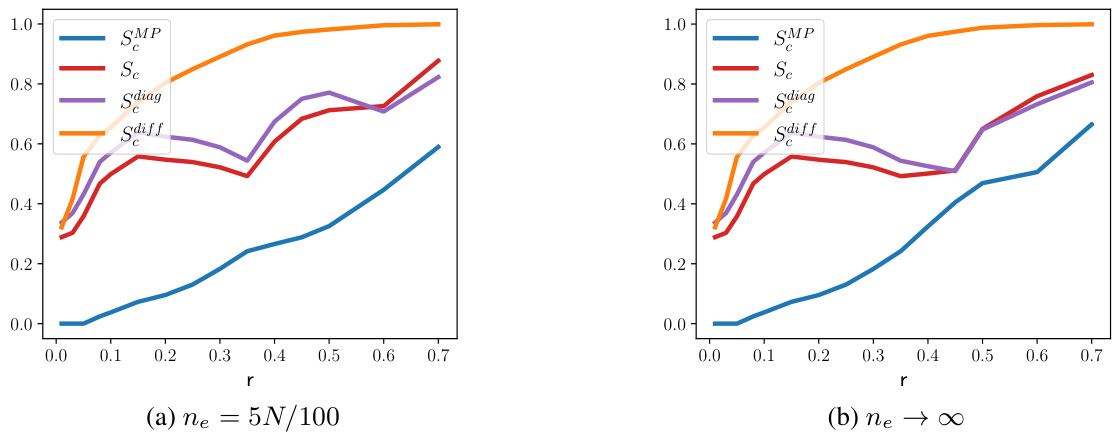
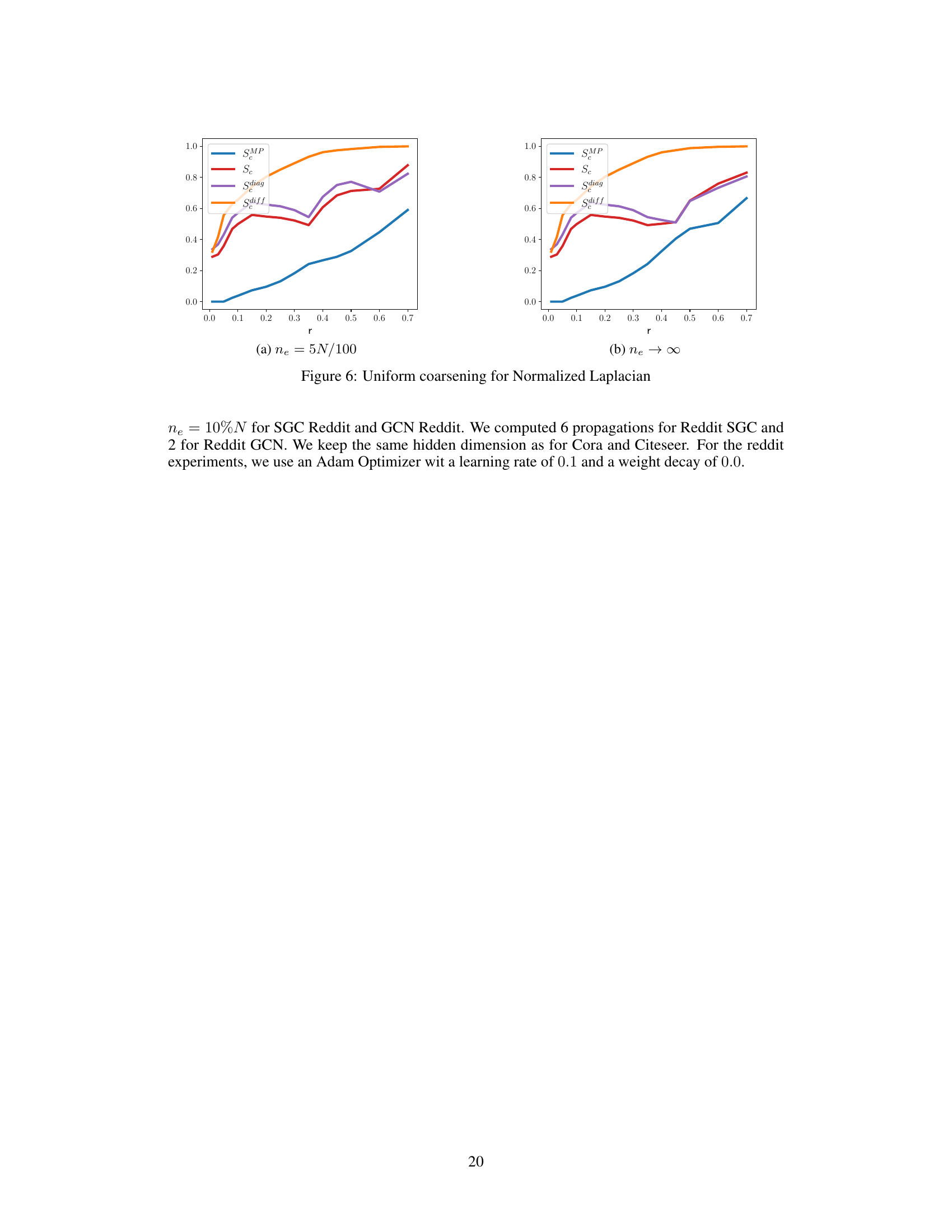
This figure shows the Message-Passing error for different propagation matrices with uniform coarsening (ne = 5N/100) and Normalized Laplacian. The x-axis represents the coarsening ratio (r), and the y-axis represents the Message-Passing error. The plot compares the proposed SMP matrix with other propagation matrices (Sc, Sdiag, Sdiff, Ssym) for different coarsening ratios. The figure helps to evaluate the effectiveness of the proposed propagation matrix for preserving message-passing guarantees during graph coarsening.
More on tables
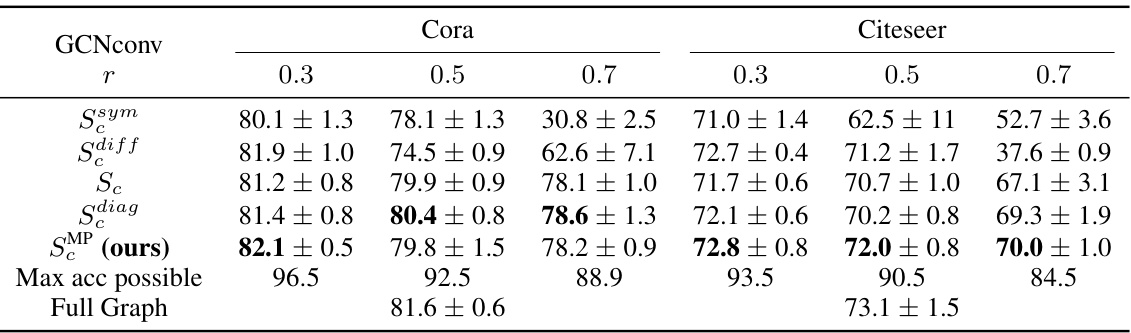
This table presents the accuracy results for node classification using the GCNconv model on Cora and Citeseer datasets with different coarsening ratios (0.3, 0.5, 0.7). It compares five different propagation matrices: SMP (the proposed method), Sc (naive), Sdiff, Sdiag, and Ssym. The results are averaged over 10 random training sets. Max accuracy possible and the full graph accuracy results are also shown for comparison.
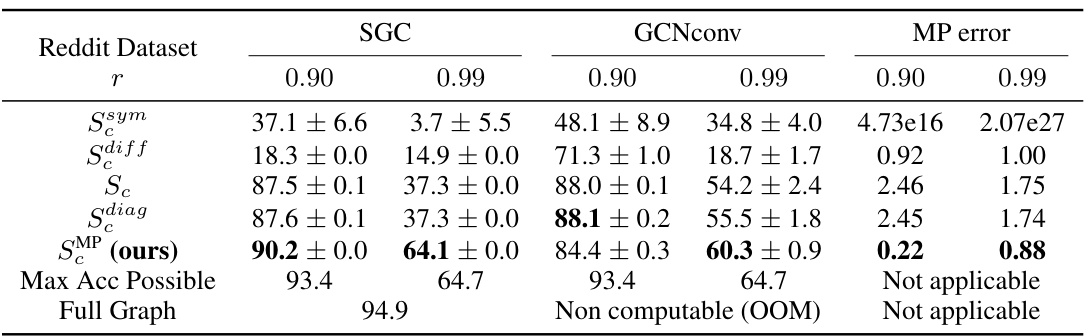
This table presents the results of node classification experiments on the Reddit dataset using different propagation matrices and coarsening ratios. It shows the accuracy achieved by various methods (Ssym, Sdiff, Sc, Sdiag, SMP) along with the message passing errors for both SGC and GCNconv models. The ‘Max Acc Possible’ row indicates the maximum achievable accuracy given the coarsening, while the ‘Full Graph’ row represents the accuracy obtained when training on the complete graph (out of memory for this dataset).

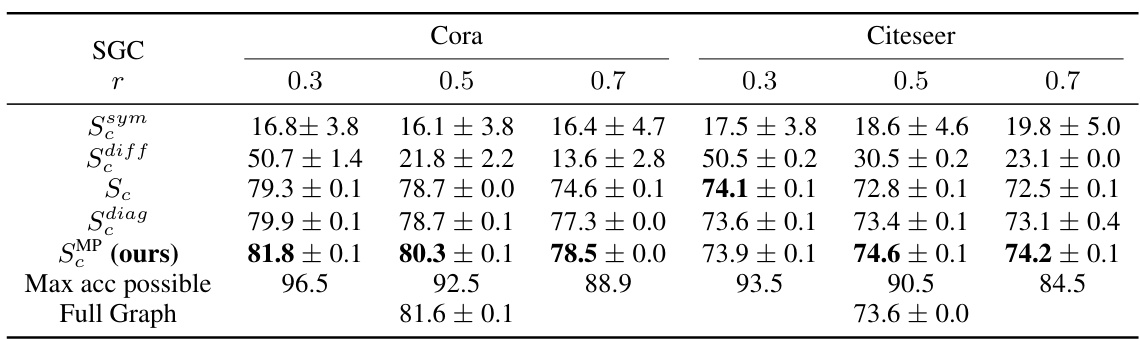
This table presents the accuracy of node classification using Simplified Graph Convolution (SGC) models with varying coarsening ratios (r = 0.3, 0.5, 0.7). It compares the performance of five different propagation matrices: SMP (the proposed method), Sdiag, Sdiff, Sc (naive choice), and Ssym. The results are shown for both the Cora and Citeseer datasets and include a ‘Max acc possible’ row representing the theoretical maximum achievable accuracy given the coarsening.

This table presents the accuracy of node classification using Simplified Graph Convolution (SGC) models on the Cora and Citeseer datasets with different coarsening ratios. It compares the performance of five different propagation matrices (SMP, Sc, Sdiag, Sdiff, and Ssym) across various coarsening ratios (0.3, 0.5, and 0.7), showing the accuracy and standard deviation for each method. The ‘Max acc possible’ row indicates the upper bound of accuracy that can be achieved with a given coarsening.

This table presents the accuracy results of node classification using Simplified Graph Convolution (SGC) with different coarsening ratios (0.3, 0.5, 0.7) on Cora and Citeseer datasets. It compares five different propagation matrices: SMP (the proposed method), Sc (naive choice), Sdiag, Sdiff, and Ssym. The accuracy is averaged over 10 random trainings. The table also shows the maximum possible accuracy achievable given the coarsening and the accuracy obtained using the full graph without coarsening for comparison.
Full paper#