Neural Collapse To Multiple Centers For Imbalanced Data

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it addresses the challenge of imbalanced data classification, a pervasive problem across many machine learning applications. By proposing a novel loss function and strategy to induce Neural Collapse to Multiple Centers (NCMC), it offers a new approach to improve generalization, which is highly relevant to current research trends in imbalanced learning. Further investigation of NCMC opens avenues for optimizing deep network architectures and improving the performance of long-tailed recognition.

Visual Insights

#

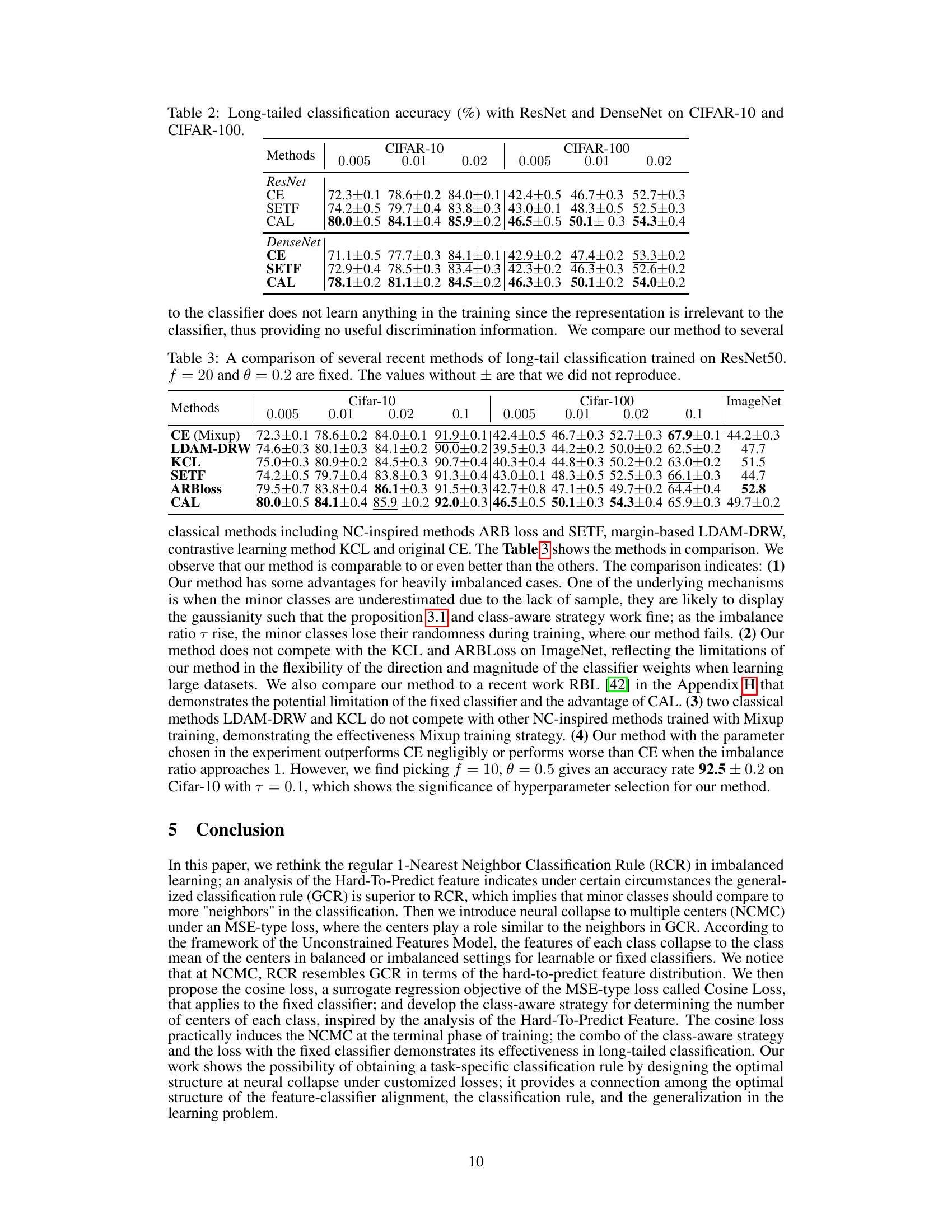
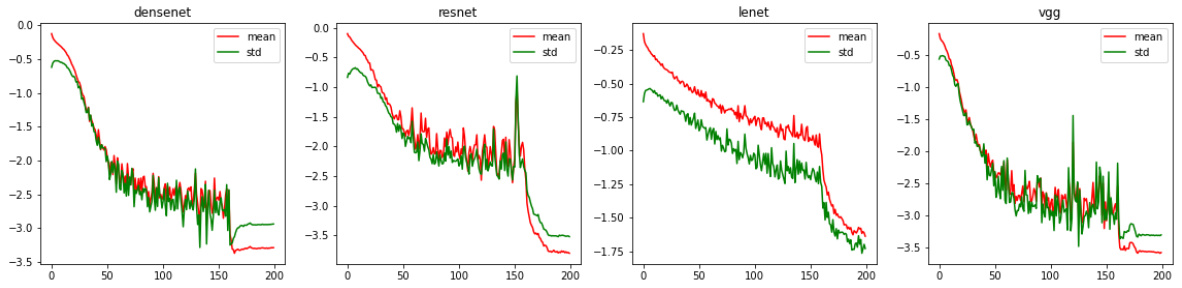
This figure shows the neural collapse curves for Average Loss (AL) and Class-Aware Loss (CAL) on CIFAR-10 and CIFAR-100 datasets with an imbalance ratio (τ) of 0.01. The plots display the average neural collapse (NC_ave), standard deviation of the neural collapse (NC_std), and variability over epochs of training. AL uses a fixed number of centers (f=20), while CAL employs a class-aware strategy to determine the number of centers for each class. The graphs illustrate how the features collapse towards their respective class centers as training progresses.

This table presents the results of an ablation study conducted to evaluate the impact of using the Mixup training method in conjunction with different classifiers and loss functions on the ResNet50 model trained on the CIFAR-100 dataset. The study examines various imbalance ratios (0.005, 0.01, 0.02) and compares the performance of different methods (CE, SETF, CAL) both with and without Mixup. The parameters f and θ for the CAL method are fixed at 20 and 0.2 respectively.

In-depth insights

#

Imbalanced Data NC

#

The concept of “Imbalanced Data NC” likely refers to the phenomenon of Neural Collapse (NC) in the context of imbalanced datasets. Standard NC research often assumes balanced class distributions; however, real-world datasets frequently exhibit class imbalance. This imbalance presents challenges as the dominant classes tend to disproportionately influence the learning process, potentially leading to suboptimal performance and the underrepresentation or misclassification of minority classes. Analyzing how NC manifests in imbalanced data is crucial because the typical properties of NC, such as the convergence of feature vectors and classifier weights to optimal geometric structures, might be affected. Research into “Imbalanced Data NC” would investigate how these structures change under class imbalance, exploring techniques to mitigate the adverse effects of the dominant classes and improve the representation of minority classes. This likely involves investigating modified loss functions, data augmentation strategies, or other methods that can encourage more balanced representation and better classification across all classes, potentially leading to improved generalization and robustness in real-world applications. A key focus would be on determining if and how the benefits of NC, like improved generalization, can be preserved or enhanced in the face of class imbalance.

Cosine Loss

#

The Cosine Loss function, as presented in the research paper, is a novel approach to address long-tailed classification challenges. It’s a regularized loss function designed to induce Neural Collapse to Multiple Centers (NCMC) in deep neural networks. The key idea behind Cosine Loss is to measure the angular distance between feature vectors and their corresponding class centers, moving away from traditional Euclidean distance. This focus on angular similarity is crucial for handling class imbalance because it emphasizes the direction rather than magnitude. The cosine similarity encourages feature vectors from the same class to cluster together, while simultaneously pushing them away from centers of other classes. The regularization term in the loss function further refines the effect by penalizing large feature vector norms. This effectively creates more discriminative feature representations by leveraging the relative orientation of the features with respect to class centers. The inclusion of hyperparameters (λ and β) provides control over the tradeoff between angular distance and magnitude regularization, making the loss adaptable to various imbalanced datasets. The class-aware strategy for determining the optimal number of centers is also critical, enabling adaptation of the loss function based on the class distribution, a significant feature that contributes to improved long-tailed classification performance. Overall, Cosine Loss, as designed and implemented, offers a theoretically sound and empirically effective way to tackle the class imbalance problem.

NCMC Analysis

#

An in-depth ‘NCMC Analysis’ would dissect the theoretical underpinnings of Neural Collapse to Multiple Centers (NCMC), exploring its behavior under various conditions. It would delve into the mathematical framework used to describe NCMC, likely focusing on the Unconstrained Feature Model (UFM) and its implications for feature and classifier weight alignment. A key aspect would be a rigorous comparison of NCMC to standard Neural Collapse (NC), highlighting how the introduction of multiple centers alters the optimal geometric structure at the terminal phase of training. The analysis would likely examine the impact of data imbalance on NCMC, potentially showing how this phenomenon can mitigate the problem of minority collapse. A critical component would involve the derivation and properties of the loss function used to induce NCMC, explaining how its design encourages the desired feature alignment to multiple class centers. Finally, it should explore the limitations of the NCMC framework, perhaps discussing its computational cost or scenarios where it might not be effective, alongside empirical results supporting or challenging its theoretical predictions.

Class-Aware Strategy

#

The Class-Aware Strategy, as described in the paper, is a crucial component for determining the number of centers for each class in the proposed NCMC framework. It directly addresses the challenge of data imbalance by dynamically adjusting the number of centers based on class size. Unlike traditional methods that use a fixed number of centers, the Class-Aware Strategy provides a more nuanced approach. This adaptive strategy is theoretically justified and empirically demonstrated to improve the performance on long-tailed classification problems. By assigning more centers to smaller classes, this approach helps mitigate the minority class collapse issue commonly seen in imbalanced datasets. The strategy’s effectiveness stems from its ability to provide more discriminative power for under-represented classes, leading to improved generalization and accuracy. Furthermore, the class-aware allocation of centers aligns well with the proposed Generalized Classification Rule (GCR), which suggests that minor classes benefit from aligning with more directions to improve classification accuracy. The strategy’s practical implementation involves a three-step process and successfully balances computational cost and performance gains. However, it’s important to note that the strategy’s hyperparameters (like the scaling factor) require careful selection to obtain optimal results, and further research into the strategy’s sensitivity to these parameters and its applicability to more complex datasets is warranted.

Future Work

#

Future research directions stemming from this Neural Collapse to Multiple Centers (NCMC) work could explore several promising avenues. Extending the theoretical framework to handle more complex network architectures and loss functions beyond the MSE-type loss and UFM model is crucial. Investigating the impact of different hyperparameter choices (such as the number of centers and the angle parameter) on the performance across various datasets and imbalance levels would provide deeper insights into the method’s behavior. Empirical studies should compare NCMC against a broader range of state-of-the-art imbalanced learning methods on larger-scale, real-world datasets to solidify the claims of comparable performance. A detailed analysis of the relationship between NCMC and generalization is warranted, possibly through theoretical bounds or empirical studies exploring the model’s robustness to distribution shifts. Finally, exploring how NCMC can be incorporated or enhanced within existing long-tail classification techniques to potentially improve their overall effectiveness is worthwhile.

More visual insights

#

More on figures

This figure is a 3D scatter plot visualizing a toy example dataset used to illustrate the concept of ‘hard-to-predict’ samples. The plot shows data points from multiple classes, each represented by a different color and shape. Data points close to the class centers are easily classified, while others far from class centers are harder to classify correctly. The purple points, specifically, are referred to as ‘hard-to-predict’ and illustrate the challenges of accurately classifying these points. The axes represent the feature space of the model.

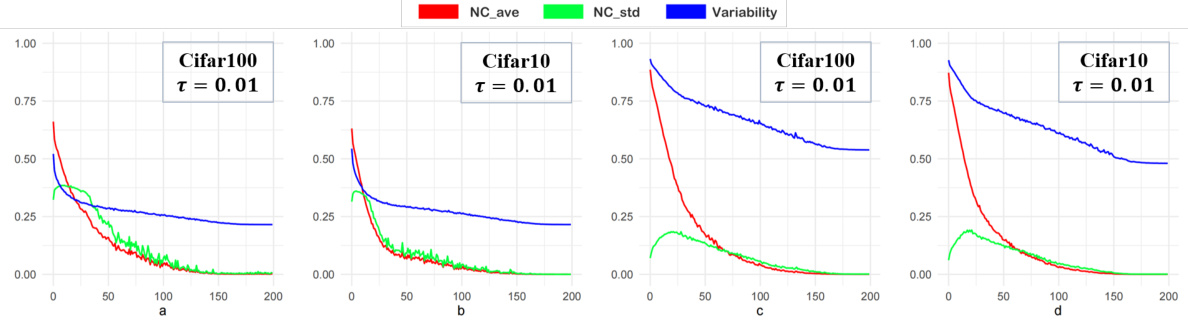
This figure provides a 3D visualization of the concept of multiple centers for two classes (Class 1 and Class 2). Each class has two centers, represented by dashed lines. The solid lines represent the vectors (w and v) that determine the centers according to the formula: Wij = cos θ * vij + sin θ * wi. This illustrates how the features of a class tend to collapse to multiple centers instead of a single center, as in standard neural collapse.

This figure shows the neural collapse curves for both the Average Loss (AL) and the Class-Aware Loss (CAL) functions. The curves illustrate the mean and standard deviation of a neural collapse metric over training epochs for two different datasets (CIFAR-10 and CIFAR-100) with varying levels of class imbalance (τ). The AL uses a fixed number of centers (f=20) for each class, while the CAL uses a class-aware strategy to determine the number of centers. The figure demonstrates that both AL and CAL induce neural collapse, with the CAL showing potentially better performance.

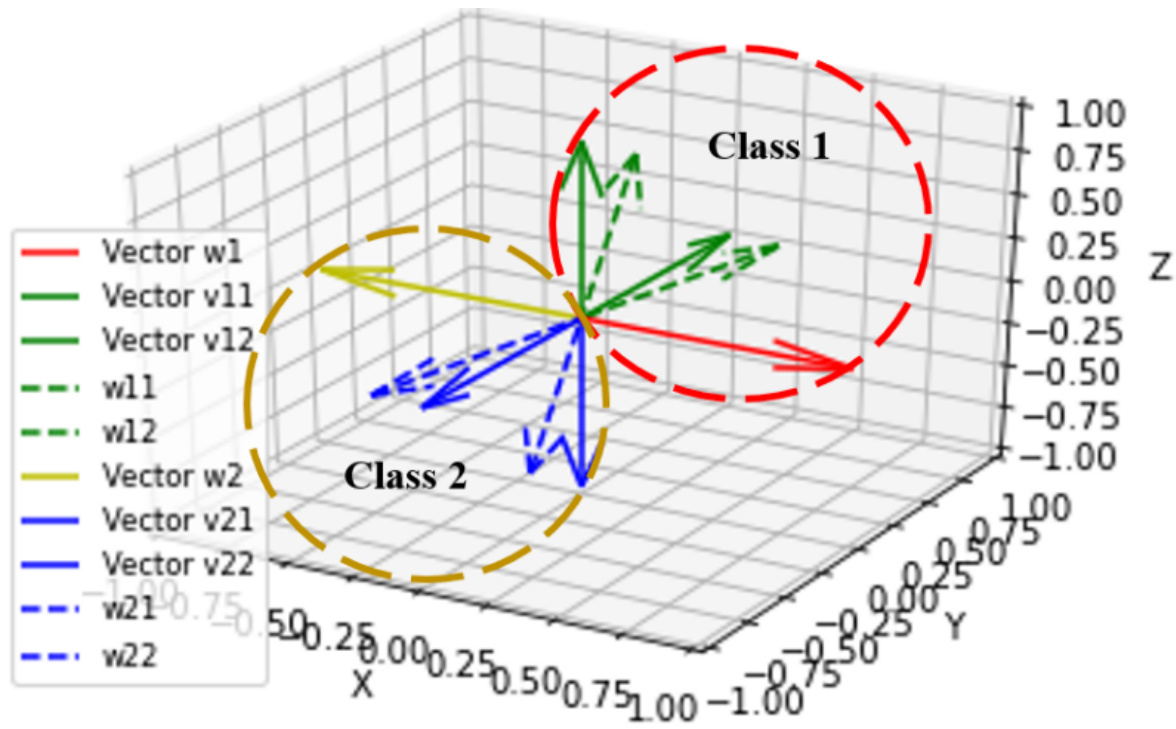
This figure shows the mean and standard deviation of the neural collapse metric (NC) for different imbalanced ratios (0.005, 0.01, 0.02, and balanced) on CIFAR-10 dataset, with and without regularization. The x-axis represents the log10-scaled NC metric value, indicating the degree of neural collapse. The y-axis shows the mean and standard deviation of this metric. The figure visualizes the impact of regularization on the neural collapse phenomenon under the proposed Loss P.

This figure shows the neural collapse curves for both Average Loss (AL) and Class-Aware Loss (CAL) on CIFAR-10 and CIFAR-100 datasets with an imbalance ratio (τ) of 0.01. The x-axis represents the training epoch, while the y-axis displays the neural collapse metric. AL uses a fixed number of centers (f=20), while CAL uses a class-aware strategy to dynamically determine the number of centers for each class. The plots illustrate how both AL and CAL induce neural collapse, showcasing the mean and standard deviation of the collapse metric over multiple runs.

This figure displays the neural collapse curves for both Average Loss (AL) and Class-Aware Loss (CAL) on CIFAR-10 and CIFAR-100 datasets with an imbalance ratio (τ) of 0.01. The plots show how the mean and standard deviation of a neural collapse metric change over training epochs. AL uses a fixed number of centers (f=20), while CAL dynamically determines the number of centers using a class-aware strategy. The plots illustrate the convergence behavior towards neural collapse for both loss functions under different settings.

More on tables

This table shows the results of long-tailed classification experiments using ResNet and DenseNet architectures on CIFAR-10 and CIFAR-100 datasets. The results are presented for different imbalance ratios (0.005, 0.01, and 0.02) and compare the performance of three methods: CE (standard cross-entropy loss), SETF (Simplex-Encoded-Labels Interpolation), and CAL (the proposed Cosine-Aware Loss). The table highlights the improved performance of CAL, especially in the more challenging imbalanced scenarios.

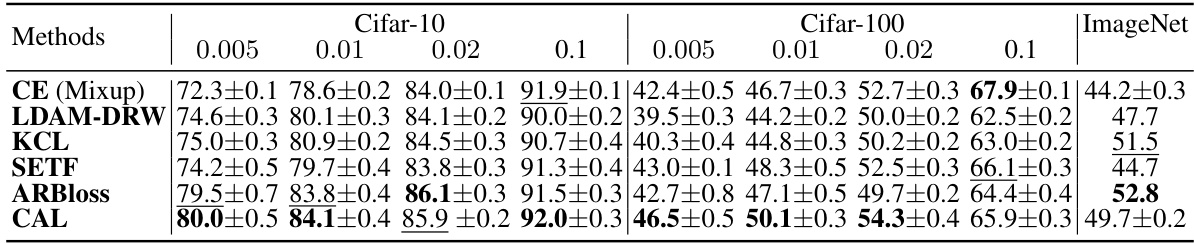
This table compares the performance of different long-tail classification methods on three datasets (CIFAR-10, CIFAR-100, and ImageNet) using ResNet50 as the backbone network. The methods compared include several recent approaches (LDAM-DRW, KCL, SETF, ARBLoss) and the proposed method (CAL). The imbalance ratio (τ) varies across different columns. Note that some values are missing because the authors did not reproduce those results. The hyperparameters f and θ are fixed at 20 and 0.2, respectively.

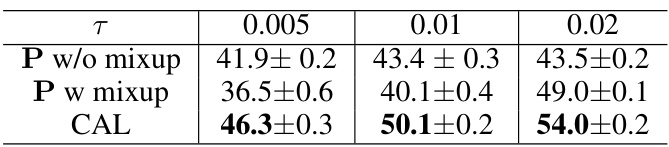
This table presents the long-tail classification results obtained using three different loss functions (Loss P without Mixup, Loss P with Mixup, and CAL) on the CIFAR-100 dataset at different imbalance ratios (τ = 0.005, 0.01, 0.02). The results are presented as the accuracy with standard deviations, showcasing the performance of each loss function under various data imbalance levels.

This table presents the results of long-tailed image classification experiments using two different network architectures (ResNet and DenseNet) on two datasets (SVHN and STL-10). The results show the accuracy achieved at different levels of class imbalance (0.005, 0.01, 0.02), comparing the performance of a standard cross-entropy loss function (CE), a fixed-classifier SETF method, and the proposed CAL method.

This table presents the ResNet50 accuracy on CIFAR-100 with an imbalance ratio of 0.005, varying hyperparameters f and θ in the proposed Cosine Regression Loss. It demonstrates how the choice of these hyperparameters impacts the model’s performance on the long-tailed classification task.

This table compares the performance of CAL and RBL methods on CIFAR-10 and CIFAR-100 datasets with different imbalance ratios. It highlights the impact of the post-hoc logit adjustment in RBL and shows that CAL outperforms RBL in some settings, but RBL with post-hoc logit adjustment is better in others.

Full paper

#