↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large-scale least squares regression is computationally expensive, especially in distributed settings. Existing sketching methods, while reducing data size, often introduce significant bias, impacting accuracy. Previous approaches to mitigate bias involved costly techniques or imposed strong assumptions, limiting their practical use. This created a need for efficient methods that minimize bias while maintaining computational efficiency.
This work introduces a novel sparse sketching method that addresses these limitations. By focusing on bias reduction rather than error minimization, the method achieves a nearly unbiased least squares estimator. It utilizes only two passes over the data, operates in optimal space complexity, and runs within current matrix multiplication time. This leads to significant advancements in distributed averaging algorithms for least squares and related tasks, improving upon various existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large datasets and distributed systems. It offers significant improvements in efficiency and scalability for least squares regression, a fundamental problem across many fields. The novel bias analysis and new sketching techniques presented are broadly applicable and can inspire new research directions in randomized linear algebra and beyond.
Visual Insights#
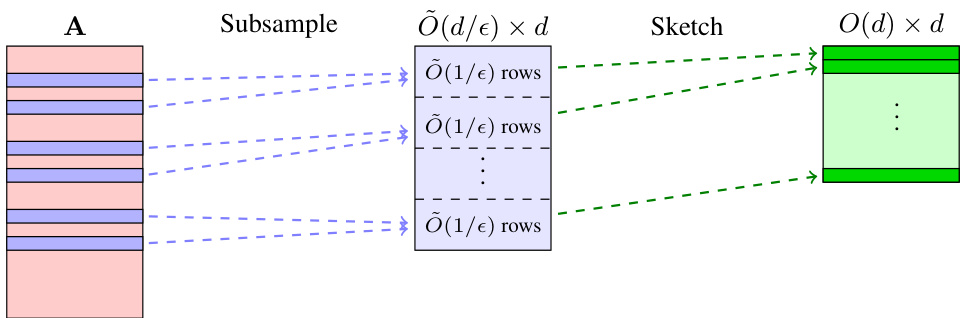
This figure illustrates the leverage score sparsification algorithm used to prove Theorem 1 in the paper. It shows how a large data matrix A is first subsampled to a smaller matrix with O(d/ε) rows. Then, a sketching matrix is applied to this subsample, creating a final sketch with only O(d) rows. The key takeaway is that while the error guarantee of the subsampled estimator is ε, the bias of the sketched estimator remains at ε. This demonstrates that a smaller sketch can achieve the same level of bias.

This table compares the time complexity and the number of parallel passes required by different methods for solving a least squares problem with a given preconditioner. The methods compared are Gaussian Sketch, Leverage Score Sampling, Determinantal Point Process, and Weighted Mb-SGD (sequential). The comparison is based on achieving a (1+ε)-approximation using O(d²log(nd)) bits of space.
In-depth insights#
Bias Reduction#
The concept of bias reduction is central to this research paper, focusing on improving the accuracy of least squares estimators within the context of matrix sketching. Traditional sketching methods prioritize minimizing error, often at the cost of increased bias. This work innovates by directly tackling bias reduction, demonstrating that in distributed settings, a nearly unbiased estimator can be recovered using computationally efficient techniques. This involves the development of novel sparse sketching methods that minimize bias, analyzed using higher-moment restricted Bai-Silverstein inequalities. The key insight is that by carefully controlling the sketch’s sparsity and leveraging statistical robustness, substantial bias reduction can be achieved without sacrificing computational efficiency. The resulting algorithms offer a promising approach to solving large-scale least squares problems in space-constrained environments, effectively mitigating the inherent limitations of traditional sketching approaches.
LESS Sketching#
Leverage Score Sparsification (LESS) sketching is a powerful technique for dimensionality reduction in large-scale data analysis. It cleverly combines the benefits of leverage score sampling with the efficiency of sparse sketching matrices. LESS excels by minimizing the bias of least squares estimators, unlike traditional sketching methods that primarily focus on minimizing error. The approach involves constructing a sparse sketching matrix where the non-zero entries are strategically placed according to the approximate leverage scores of the original data matrix. This results in a significant reduction in the size of the data while maintaining near-unbiasedness of the resulting estimators, particularly crucial in distributed computing scenarios. The resulting low-bias property is particularly valuable for communication-efficient distributed algorithms. Moreover, the inherent sparsity of LESS embeddings translates to significant computational advantages, making it computationally efficient compared to dense sketching methods. A key advantage is its optimal space complexity, enabling it to handle massive datasets with limited memory. This technique thus offers a compelling trade-off between bias reduction, computational efficiency, and memory usage, making it a noteworthy advancement in sketching methods for least squares regression and related tasks.
Distributed Setting#
The research paper explores the advantages of applying sketching methods in a distributed computing environment to solve least squares problems. A key insight is that minimizing bias, rather than simply error, in the distributed setting leads to significant improvements in accuracy and efficiency. The authors propose a novel sparse sketching method, demonstrating that near-unbiased estimates can be obtained in optimal space and time complexity. The distributed averaging algorithm leverages these low-bias estimators, substantially improving upon existing communication-efficient approaches. Higher-moment restricted Bai-Silverstein inequalities are introduced to provide sharp bias analysis, showcasing a sharp characterization of bias dependence on sketch sparsity. The algorithm’s efficiency and scalability for large-scale least squares regression are highlighted, making it suitable for parallel processing environments and resource-constrained settings. Practical benefits are demonstrated via experiments on benchmark datasets, illustrating that compression of data via sketching maintains accuracy through averaging despite an increase in variance.
Higher-Moment Analysis#
Higher-moment analysis extends traditional methods by examining moments beyond the second moment (variance). In the context of sketching-based estimators for least squares problems, it’s crucial because standard analyses often rely on second-moment properties, which may not fully capture the behavior of sparse sketching matrices. Higher-moment analysis provides a more comprehensive understanding of the estimator’s bias, especially when dealing with sparse matrices that exhibit non-Gaussian behavior. By considering higher moments, it allows for sharper characterizations of the bias’s dependence on sketch sparsity, leading to tighter bounds and potentially more efficient algorithms. This analysis often involves sophisticated techniques from random matrix theory and may lead to new inequalities or refinements of existing ones, demonstrating the estimator’s statistical robustness, such as sharp confidence intervals and effective inference tools.
Future Directions#
Future research could explore extensions to handle non-linear models and scenarios with non-convex loss functions. The current work focuses on least squares, a specific case. Investigating the applicability and bias-reduction techniques for broader machine learning tasks would significantly impact practical applications. Moreover, the optimal choice and efficient estimation of sketching matrix sparsity requires further investigation. While the paper provides a characterization, a more refined understanding, potentially data-adaptive methods, could lead to improved performance in practice. Finally, theoretical bounds could be tightened, and the algorithmic runtime could be optimized. The current bounds provide an important initial characterization but may not reflect the empirical performance. Further investigation into the distributional properties of the estimates could also prove valuable.
More visual insights#
More on figures

This figure displays the results of a distributed averaging experiment conducted on two datasets: YearPredictionMSD and Abalone. The experiment evaluates the effectiveness of using sparse sketching to compress data while maintaining near-unbiasedness in least squares estimation. Different lines represent different sketch sizes and non-zero entries per row, but with the same total cost, demonstrating that compressing the data does not lead to increased bias, despite reducing the error, showcasing a ‘free lunch’ in distributed averaging.
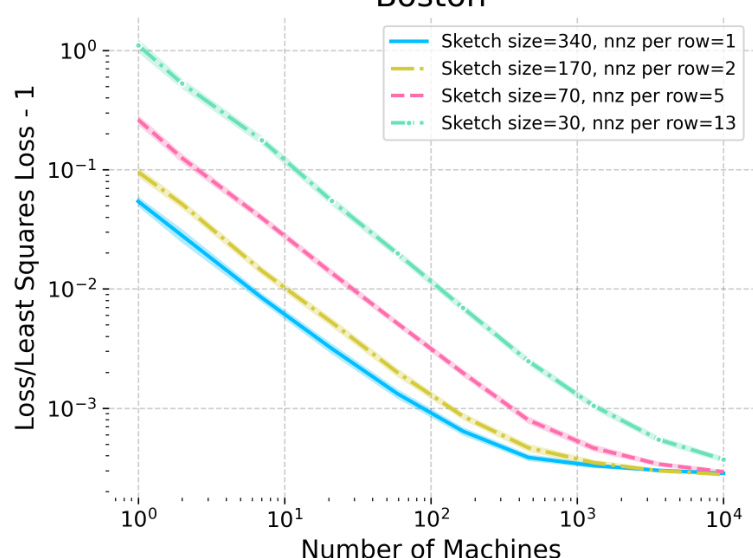
The figure shows the results of a distributed averaging experiment using sparse sketching on two datasets, YearPredictionMSD and Abalone. The experiment demonstrates that using sparse sketching to compress the data does not introduce significant bias, while maintaining near-unbiasedness and without increasing the computational cost. Multiple lines on the graph show the effect of varying the sketch size and sparsity, all while keeping the total computational cost of sketching constant.
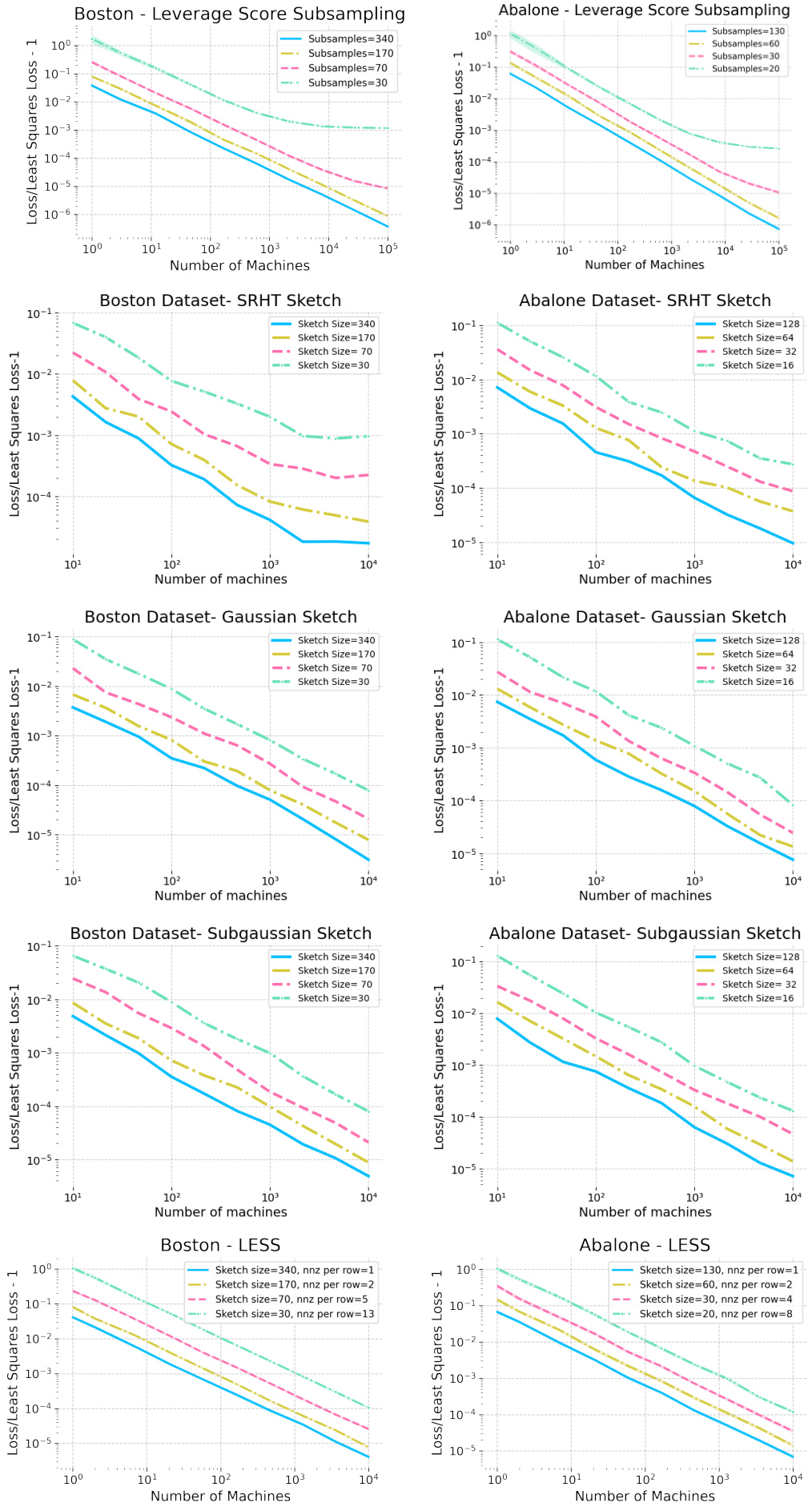
The figure displays the results of a distributed averaging experiment conducted on the YearPredictionMSD and Abalone datasets. The experiment compares the relative error of averaged sketched-and-solved least squares estimators using different sketching techniques with varying sketch sizes and sparsity. It demonstrates that sparse sketching compresses data effectively while maintaining low bias, suggesting that in distributed settings, the bias is minimal even when the space on each machine is limited. The results for the Boston dataset are available in Appendix F.
Full paper#