Semidefinite Relaxations of the Gromov-Wasserstein Distance

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents a novel semi-definite programming (SDP) relaxation for the Gromov-Wasserstein (GW) distance, a challenging problem in optimal transport. This offers a tractable algorithm to compute globally optimal solutions (in some instances), unlike existing methods that only find locally optimal solutions. The proposed approach is shown to frequently compute globally optimal solutions in numerical experiments. This work opens new avenues for research in optimal transport, particularly for applications involving structured data and complex cost matrices where existing methods fall short. The availability of a Python implementation further enhances its accessibility and impact.

Visual Insights

#

This figure shows a comparison of optimal transport plans obtained using three different methods: GW-SDP (the authors’ proposed method), CG-GW (a conditional gradient descent method), and entropic OT. The left panel displays the 2D source distribution (blue) and the 3D target distribution (red). The right panel shows the optimal transport plans generated by each method. Note that the GW-SDP and CG-GW methods produce sparse transport plans (many zero entries in the transport matrix), while the entropic OT method does not. The sparsity indicates that these methods primarily match similar points in the two distributions while the entropic OT method smooths this process.

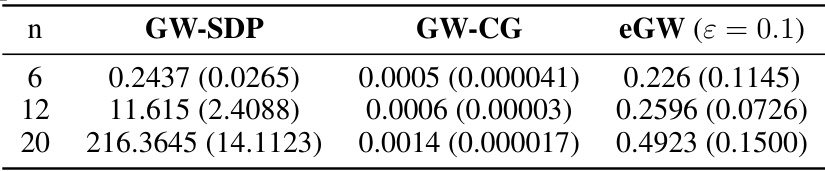
This table shows the average runtime in seconds for the Gaussian matching experiment shown in Figure 1a of the paper. The runtime is broken down by the number of samples (n = 6, 12, 20) and the algorithm used (GW-SDP, GW-CG, eGW). Standard deviations are included in parentheses. This illustrates the computational cost comparison between the proposed GW-SDP method and existing methods.

In-depth insights

#

SDP-GW Relaxation

#

The heading ‘SDP-GW Relaxation’ suggests a novel approach to solving the Gromov-Wasserstein (GW) distance problem, a computationally challenging task in optimal transport. The core idea is to leverage semidefinite programming (SDP), a powerful technique for tackling non-convex optimization problems. By formulating the GW distance calculation as an SDP, the method aims to overcome the limitations of existing GW solvers, which often only provide locally optimal solutions. This SDP relaxation likely involves reformulating the GW problem’s objective function and constraints into a form suitable for SDP solvers. The benefit of using SDP is that it guarantees finding a globally optimal solution, as opposed to local optima, provided certain conditions are met. This global optimality is the key advantage claimed, though the computational cost of SDP might increase depending on the problem size. Tractability becomes a crucial factor to consider, as the computational complexity of SDP can be high. Therefore, the effectiveness hinges on the trade-off between achieving global optimality and maintaining computational feasibility. The paper likely provides numerical results demonstrating the efficiency and accuracy of the SDP-GW relaxation compared to other existing methods. Furthermore, the authors may explore the theoretical properties of their relaxation, demonstrating its tightness and providing bounds on the approximation error.

Global Optimality

#

The concept of global optimality is central to the paper’s exploration of semidefinite programming (SDP) relaxations for the Gromov-Wasserstein (GW) distance. The GW distance, while powerful for comparing objects in different spaces, is notoriously difficult to solve due to its non-convex nature. Existing methods often get trapped in local optima, failing to find the true global minimum. The paper’s key contribution is the introduction of a strong SDP relaxation that frequently finds the globally optimal solution. This is a significant advance because SDPs are efficiently solvable using polynomial-time algorithms. The authors provide a theoretical framework for understanding when this relaxation is exact, offering a certificate of global optimality in specific cases. Moreover, they demonstrate empirically that their approach outperforms existing GW solvers, often finding superior solutions with comparable or better computational cost. The frequent attainment of global optima, even without guarantees in all cases, highlights the practical significance of this approach. The ability to certify global optimality in some cases, combined with frequent empirical success, positions this work as a major contribution to the field of optimal transport and its applications in graph matching and other domains.

Gaussian Matching

#

The experiment section, “Gaussian Matching”, demonstrates the efficacy of the proposed SDP relaxation for the Gromov-Wasserstein distance. It focuses on matching Gaussian distributions in differing dimensional spaces (R2 and R3), a scenario where traditional optimal transport methods are inapplicable. The SDP approach consistently outperforms existing methods (Conditional Gradient and Entropic GW) in terms of objective function value, indicating superior accuracy in finding globally optimal transport plans. Furthermore, the results show that the SDP solutions produce transport plans with comparable sparsity to the Conditional Gradient method, a desirable property in many applications. The experiment also explores the impact of varying the number of sample points, showing the robustness of the SDP relaxation while highlighting potential efficiency benefits over traditional methods, especially when the number of sample points is smaller. This Gaussian matching experiment serves as a strong validation of the proposed method’s capabilities and its potential to provide substantial improvements in applications involving comparisons of probability distributions across disparate spaces.

Computational Cost

#

The computational cost of Gromov-Wasserstein (GW) distance computation is a significant bottleneck, especially for large-scale datasets. Existing methods often rely on iterative algorithms that converge slowly, leading to substantial runtime issues. The paper addresses this by proposing a semidefinite programming (SDP) relaxation of the GW distance, which offers a potential pathway towards polynomial-time solutions. While the SDP relaxation itself involves solving a computationally intensive problem, the authors argue it’s a stronger approach for finding globally optimal solutions than existing iterative solvers. However, even SDP solvers can be costly. The paper emphasizes the importance of developing specialized solvers tailored to exploit the unique structure of the GW problem to further mitigate the computational burden. The numerical experiments highlight the trade-off between computational cost and global optimality: While the SDP method is slower than local optimization methods for smaller datasets, the trade-off is worthwhile in obtaining the globally optimal solution, especially as the dataset size grows. Future work should focus on developing efficient and specialized SDP solvers optimized for GW distance calculations.

Future Research

#

Future research directions stemming from this work on semidefinite programming (SDP) relaxations for the Gromov-Wasserstein (GW) distance could focus on several key areas. Improving computational efficiency is paramount, as the current SDP formulation’s scalability is limited. Exploring specialized solvers that leverage the problem’s structure, such as low-rank techniques, would be crucial. Investigating the tightness of the SDP relaxation across different data types and cost functions is another important avenue. Determining which problem instances yield globally optimal solutions via the SDP relaxation is key to understanding its strengths and limitations. Further work could explore extensions to handle structured data more effectively, potentially incorporating domain-specific constraints. Finally, applying the framework to related problems, such as the Gromov-Hausdorff distance, and exploring connections with other optimization techniques, like moment-sum-of-squares relaxations, would provide significant advancements in optimal transport research. A complete characterization of computationally tractable GW instances would be of theoretical interest.

More visual insights

#

More on figures

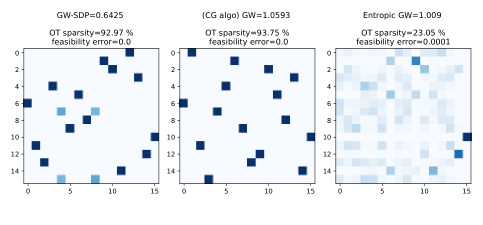
This figure shows a comparison of optimal transport plans obtained by three different methods: GW-SDP (the proposed method), CG-GW (a conditional gradient descent method), and entropic OT. The left panel visualizes the source (2D) and target (3D) distributions. The right panel displays the optimal transport plans generated by each method, highlighting the sparsity of GW-SDP and CG-GW compared to the entropic OT method.

This figure shows the results of an experiment comparing the performance of the proposed GW-SDP algorithm against Conditional Gradient (CG-GW) and entropic GW methods on a Gaussian matching task. The left panel displays the objective function values for each algorithm as the number of sample points increases. The right panel shows the approximation ratio, calculated as the ratio of the objective function value of each algorithm to that of the optimal solution obtained using GW-SDP. The results suggest that GW-SDP consistently achieves lower objective values and frequently computes globally optimal solutions.

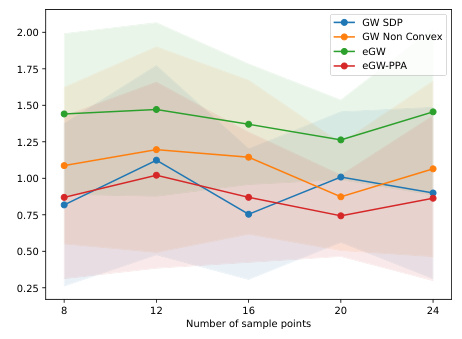
The figure shows the results of Gaussian matching experiments where the number of sample points in one distribution is fixed (n=8), while the number of sample points (m) in the other distribution varies. It compares the objective function values (GW distances) obtained using four different methods: GW-SDP (the proposed method), GW Non-Convex (conditional gradient descent solver), eGW (entropic GW solver), and eGW-PPA. The plot shows the average objective function value over 20 runs for each value of m, illustrating that the proposed GW-SDP method consistently yields smaller objective function values compared to the other methods.

This figure shows the results of Gaussian matching experiments where the number of sample points in one distribution is fixed (n=8), and the number of sample points (m) in the other distribution is varied. It presents two subplots. The left subplot displays the objective values obtained using different solvers (GW-SDP, GW Non-Convex, eGW). The right subplot shows the approximation gap for GW-SDP, indicating how close the SDP relaxation solution is to the globally optimal solution for the GW problem. The approximation gap is calculated by dividing the objective value of the SDP solution by the objective value of the true optimal GW solution. A value of 1.0 signifies that the SDP relaxation found the globally optimal solution. The experiment was repeated 20 times, and the average results are shown.

This figure compares the performance of three different methods (GW-SDP, GW-CG, and eGW) and their fused counterparts (Fused-GW-SDP, Fused-GW-CG, and Fused-eGW) on a graph matching task. The methods are applied to two synthetic graphs generated from stochastic block models (SBMs) with different numbers of clusters. The top row shows the results using the standard Gromov-Wasserstein (GW) distance, while the bottom row shows the results using the Fused Gromov-Wasserstein (FGW) distance. Each image represents the optimal transport plan obtained by each method, visualized by connecting corresponding nodes between the two graphs. The numbers below the images show the objective function values achieved by each method. The figure visually demonstrates that the proposed GW-SDP method consistently achieves lower objective values than the alternative methods. This indicates that GW-SDP achieves better results in this specific scenario.

This figure shows two examples of correspondences between 3D objects found by the GW-SDP algorithm. The left panel shows a one-to-one mapping between two elephants, and the right panel shows a one-to-one mapping between an elephant and a cat. The correspondences are visualized by lines connecting corresponding points on the two objects.

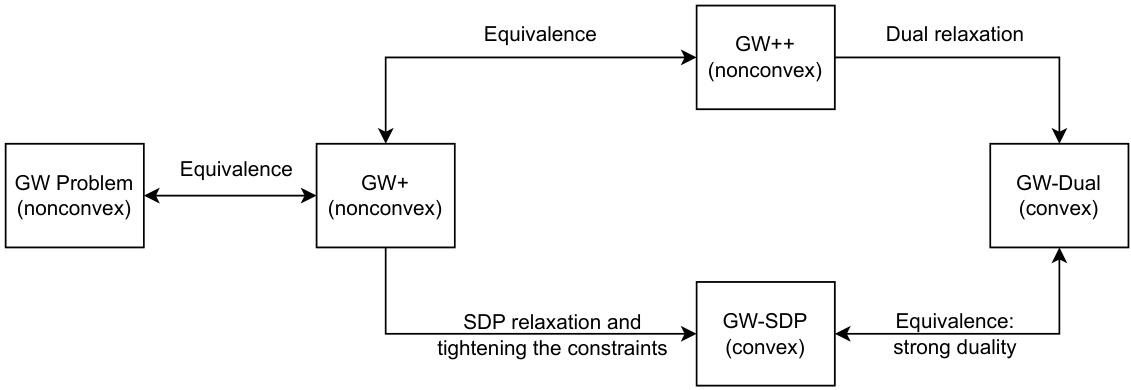
This figure illustrates the relationships between several formulations of the Gromov-Wasserstein (GW) problem and its dual. It shows how the original non-convex GW problem is first reformulated as GW+ and GW++. The GW++ formulation, which includes additional redundant constraints, is then used to derive the convex GW-Dual problem through Lagrangian dualization. A separate convex relaxation (GW-SDP) is also developed, and the figure demonstrates the equivalence and strong duality that exists between GW-SDP and GW-Dual.

This figure visualizes the results of applying the proposed GW-SDP algorithm to compute the barycenter of a set of noisy circular graphs. (a) shows nine examples of the noisy circular graphs used as input to the algorithm, each with a slightly different structure. (b) displays the resulting barycenter graph computed by GW-SDP, which represents a kind of average structure among the input graphs. The figure illustrates the algorithm’s capability to find a meaningful representative structure from a collection of similar but not identical graphs.

More on tables

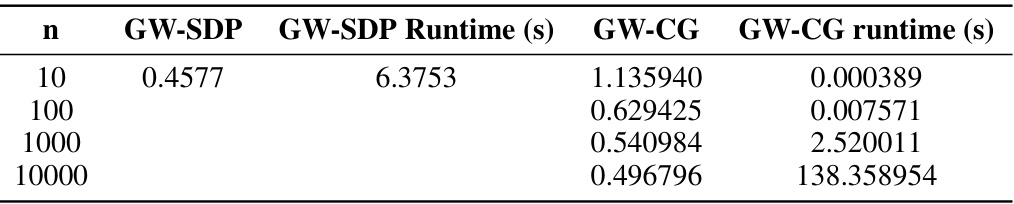
This table compares the performance of the GW-SDP solver and the GW-CG solver for the Gaussian matching experiment with different numbers of sample points. It shows the objective values obtained by each solver and their corresponding runtimes for various sample sizes (n = 10, 100, 1000, 10000). The results demonstrate the trade-off between the accuracy and efficiency of the two approaches, highlighting the strengths and weaknesses of each method in terms of computational cost and quality of solution.

This table shows the Gromov-Wasserstein (GW) distances calculated using three different methods (GW-SDP, GW-CG, and eGW-PPA) for pairs of 3D shapes from the categories elephant, cat, and horse. The results demonstrate that the GW-SDP method consistently produces the lowest GW distance values, indicating its effectiveness in shape matching compared to existing methods.

Full paper

#