Meta-Reinforcement Learning with Universal Policy Adaptation: Provable Near-Optimality under All-task Optimum Comparator

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for meta-reinforcement learning (meta-RL) researchers because it offers provable near-optimality guarantees under all-task optimum comparators, a significant advancement over existing methods. It also introduces a novel universal policy optimization algorithm, applicable to various existing meta-RL approaches, widening its impact and providing theoretical backing. Furthermore, its rigorous analysis and empirical validation of the upper bound on the expected optimality gap are invaluable for advancing meta-RL.

Visual Insights

#

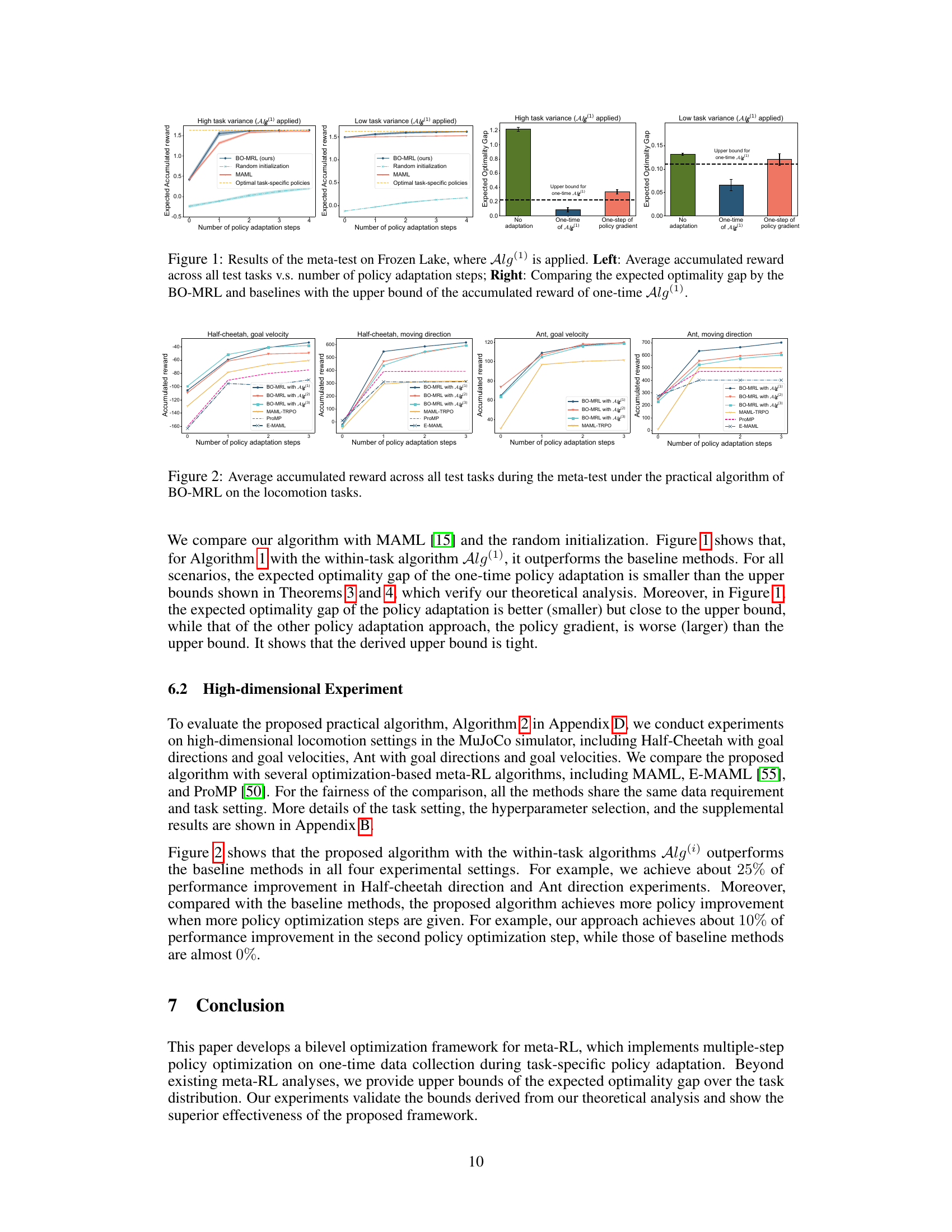
This figure displays the results of the meta-test on the Frozen Lake environment using Alg(1) in the BO-MRL framework. The left panel shows the average accumulated reward across all test tasks plotted against the number of policy adaptation steps. The BO-MRL approach is compared against baselines like random initialization and MAML. The right panel focuses on the expected optimality gap, comparing BO-MRL’s performance to the upper bound of the accumulated reward achieved with a single application of Alg(1). This illustrates BO-MRL’s efficiency in leveraging data collected from a single policy adaptation.

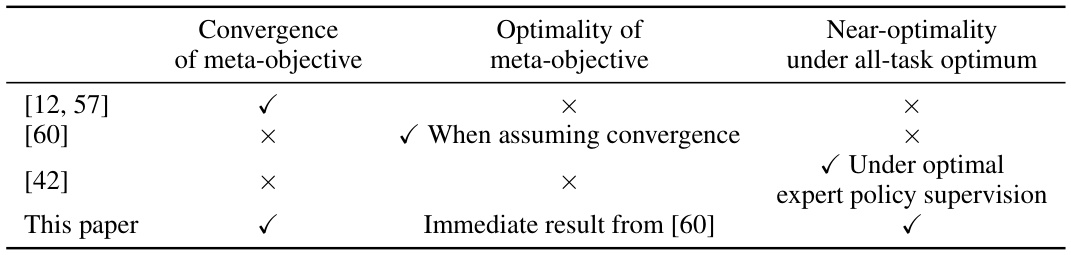
The table summarizes the theoretical advancements in meta-reinforcement learning (meta-RL) research, comparing several key aspects of different meta-RL algorithms, including this paper’s contribution. It shows which algorithms achieve convergence of the meta-objective, optimality of the meta-objective (with or without convergence assumptions), and near-optimality under the all-task optimum comparator. The table highlights the unique contributions of this work compared to prior research.

In-depth insights

#

Universal Policy

#

A universal policy, in the context of meta-reinforcement learning, aims to create a single policy that can effectively adapt to a wide range of tasks. This contrasts with task-specific policies, which are optimized for individual tasks. The core idea is to learn a meta-prior, a representation of shared knowledge across tasks, from which task-specific policies can be efficiently adapted. This approach leverages the similarities between tasks to improve data efficiency and generalization, reducing the need for extensive training data on each new task. A key challenge is balancing the capacity of the universal policy to adapt to diverse tasks with its ability to perform well on any given task. Universal policies are particularly valuable in real-world scenarios where exposure to many diverse tasks is common and collecting vast amounts of data for each task is impractical. Successful designs for universal policies rely heavily on effective meta-learning algorithms capable of learning a powerful meta-prior that balances generalization and performance. Furthermore, the theoretical analysis of such policies is critical to ensure provable performance bounds across all tasks. Thus, the study of universal policies is a crucial step toward creating truly adaptable and robust reinforcement learning agents.

Bilevel Optimization

#

Bilevel optimization is a powerful technique for tackling problems involving nested optimization, where one optimization problem is embedded within another. In machine learning, it is particularly useful for meta-learning, where an outer loop optimizes a hyperparameter or meta-policy, and the inner loop optimizes model parameters or task-specific policies for individual tasks. The outer loop aims for generalizability across tasks. A key challenge lies in computing the gradient of the outer objective with respect to the inner optimization’s solution. This necessitates techniques like implicit differentiation, which can be computationally expensive. Despite this, bilevel optimization offers a principled way to learn shared knowledge from multiple tasks efficiently. The theoretical analysis of bilevel optimization is complex, typically involving non-convex optimization and convergence guarantees that depend on specific assumptions about the problem structure. However, it offers a strong framework for meta-learning, enabling the derivation of upper bounds on the distance between adapted policies and task-specific optimal policies, thereby quantifying generalizability. The effectiveness of bilevel optimization approaches often hinges on carefully choosing the inner optimization algorithm and using appropriate hyperparameters.

Optimality Bounds

#

The optimality bounds section of a research paper is crucial for establishing the theoretical guarantees of a proposed algorithm. It provides a quantitative measure of how close the algorithm’s performance is to the optimal solution, typically expressed as an upper bound on the difference between the algorithm’s output and the optimal solution. A tight bound is highly desirable, as it indicates strong theoretical performance. The derivation of these bounds often involves intricate mathematical analysis, leveraging properties of the problem’s structure, the algorithm’s design, and relevant assumptions. The assumptions made play a critical role, as they often simplify the analysis but might not fully capture the real-world complexity. Discussing the implications of these assumptions and exploring the sensitivity of the bounds to their violation is key. Empirical validation is essential, comparing the theoretical bounds with the algorithm’s actual performance to assess the bound’s tightness and the algorithm’s practical efficacy. A discrepancy between the theoretical and empirical results could indicate limitations of either the algorithm or the analysis itself, requiring further investigation. Overall, the optimality bounds analysis offers significant value for assessing the robustness and generalizability of the developed method.

Meta-RL Analysis

#

A thorough meta-RL analysis would delve into the theoretical underpinnings of the proposed methods, examining their convergence properties, sample complexity, and generalization capabilities. Provable guarantees of optimality or near-optimality are crucial, especially under all-task optimum comparators, demonstrating the algorithm’s robustness and effectiveness across diverse tasks. The analysis should also cover the impact of hyperparameter choices on performance and provide insights into the algorithm’s scalability and computational efficiency. A detailed comparison with existing meta-RL approaches, highlighting the strengths and weaknesses of each method and justifying the selection of specific techniques, is necessary. Furthermore, the analysis should address the limitations of the theoretical framework, acknowledging the assumptions made and their potential impact on the results. Finally, empirical validation through comprehensive experiments on diverse benchmarks is crucial for substantiating the theoretical claims and demonstrating the practical applicability of the proposed methods.

High-dim. Results

#

A section titled ‘High-dim. Results’ in a research paper would likely present findings from experiments conducted on high-dimensional datasets or problems. This is crucial because many real-world applications involve high dimensionality, where traditional methods often struggle. The results would show how the proposed approach performs in such complex scenarios, possibly including comparisons to existing methods. Key metrics might include accuracy, efficiency, and generalization ability, comparing performance across different dimensions. Success in high-dimensional settings strongly suggests practical applicability and robustness of the approach, as it addresses the ‘curse of dimensionality.’ A detailed analysis of these results would be essential for evaluating the efficacy and scalability of the proposed method, providing crucial evidence of its usefulness in practical settings. The discussion might involve limitations observed in higher dimensions and potential future improvements. Ultimately, this section aims to demonstrate that the research is not merely theoretical but also practically relevant and capable of handling realistic challenges.

More visual insights

#

More on figures

This figure compares the performance of the proposed BO-MRL algorithm against several baseline methods (MAML, E-MAML, ProMP, and MAML-TRPO) across four locomotion tasks in the MuJoCo simulator. The tasks involve Half-Cheetah with goal directions and velocities, and Ant with goal directions and velocities. The x-axis represents the number of policy adaptation steps, and the y-axis shows the average accumulated reward across all test tasks. The figure demonstrates that the proposed BO-MRL algorithm consistently achieves higher average accumulated reward than the baseline methods for all four tasks, showcasing its superior performance in high-dimensional environments.

This figure shows the results of applying Algorithm 1 with the Alg(2) within-task algorithm to the Frozen Lake environment. The left panel displays the average accumulated reward achieved across all test tasks, plotted against the number of policy adaptation steps. This demonstrates the performance of the proposed BO-MRL method compared to baselines like MAML and random initialization. The right panel focuses on the expected optimality gap, comparing BO-MRL’s performance to the upper bound derived from the theoretical analysis. This comparison shows how close the BO-MRL method gets to the optimal policy.

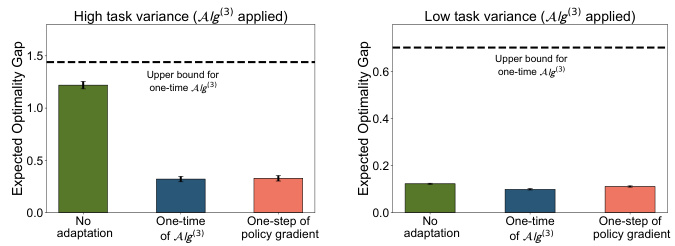
This figure displays the results of the BO-MRL algorithm on the Frozen Lake environment, specifically using the Alg(3) within-task algorithm. It compares the expected optimality gap (the difference between the optimal policy and the policy obtained by the algorithm) for three scenarios: no policy adaptation, a single one-time adaptation using Alg(3), and one step of policy gradient adaptation. The results are shown separately for high and low task variance distributions. A horizontal dashed line represents the theoretical upper bound derived in the paper for the one-time Alg(3) policy adaptation. This figure visually verifies the theoretical upper bounds and demonstrates the performance improvement of the BO-MRL approach.

This figure displays the average accumulated rewards obtained during meta-testing on four MuJoCo locomotion tasks using the practical BO-MRL algorithm. The tasks are Half-cheetah with goal velocity, Half-cheetah with goal direction, Ant with goal velocity, and Ant with goal direction. Results are shown for different numbers of policy adaptation steps (1, 2, and 3). The BO-MRL algorithm’s performance is compared against several baseline meta-reinforcement learning methods (MAML-TRPO and ProMP). The graph illustrates how BO-MRL’s performance improves over the baselines, and how that improvement increases with more policy adaptation steps, showing better generalization and adaptation ability.

Full paper

#