QVAE-Mole: The Quantum VAE with Spherical Latent Variable Learning for 3-D Molecule Generation

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents the first full quantum variational autoencoder (QVAE) for 3D molecule generation, a significant advancement in the field of quantum machine learning and drug discovery. It addresses limitations of previous methods by using a novel quantum encoding scheme and a von Mises-Fisher distributed latent space, achieving competitive performance with significantly reduced parameters. This opens avenues for exploring quantum advantages in other applications that involve generating complex 3D structures.

Visual Insights

#

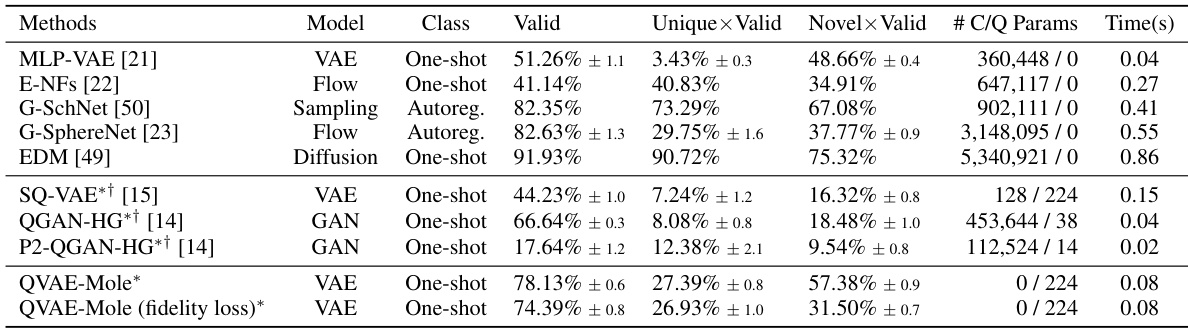
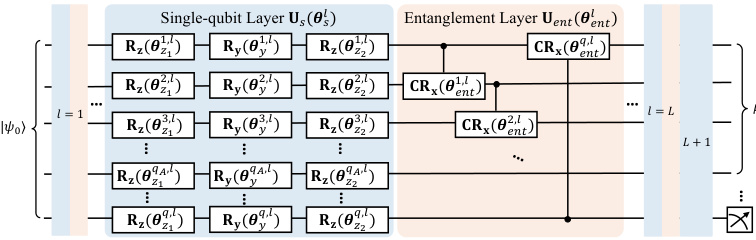
This figure illustrates the architecture of QVAE-Mole and QCVAE-Mole. It shows how classical molecular data is encoded into a quantum state using amplitude encoding, then processed by a quantum encoder to produce a latent variable sampled from a von Mises-Fisher (vMF) distribution. This latent variable is then decoded by a quantum decoder to reconstruct the molecule. The conditional version, QCVAE-Mole, incorporates conditional vectors to generate molecules with specific properties.

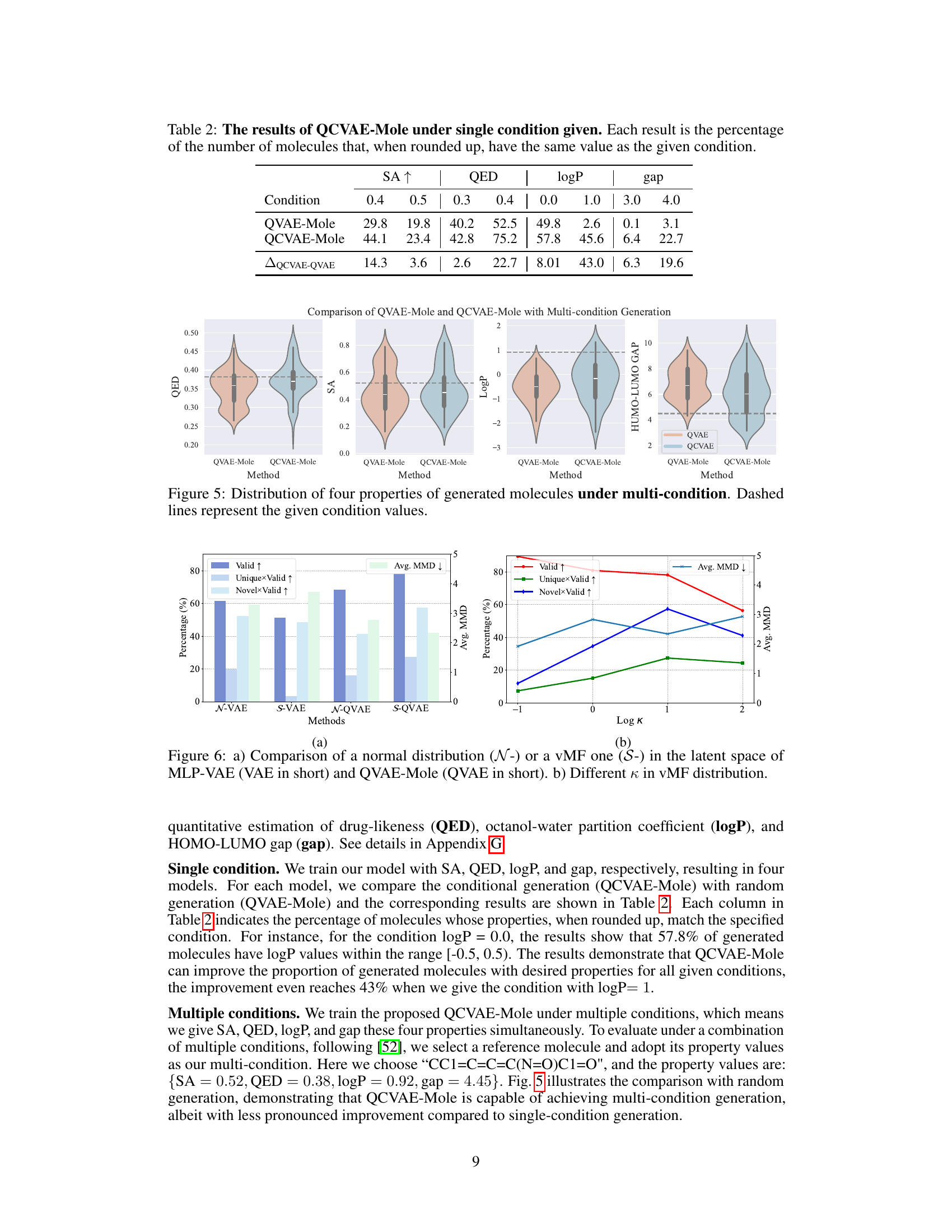
This table compares the performance of various methods for 3D molecule generation on the QM9 dataset. Metrics include the percentage of valid molecules, uniqueness, novelty, and the number of classical and quantum parameters used by each model. The inference time per molecule is also included. The table highlights the performance of the proposed QVAE-Mole model compared to state-of-the-art classical and quantum methods.

In-depth insights

#

Quantum VAE for 3D

#

The concept of a ‘Quantum VAE for 3D’ is intriguing, suggesting the application of Variational Autoencoders (VAEs) within a quantum computing framework to generate 3-dimensional data. This approach merges the strengths of VAEs—their ability to learn efficient latent representations and generate new data points—with the potential computational advantages of quantum computing, particularly in handling high-dimensional data like 3D molecular structures. A key challenge would be designing efficient quantum circuits that can encode and decode 3D information. The choice of the latent space representation is critical, as is the development of quantum-friendly loss functions to guide the learning process. Success would likely depend on advances in near-term quantum hardware capabilities and algorithms. The practical application to 3D molecule generation is particularly relevant, as it could potentially accelerate drug discovery and materials science by generating novel molecules with desired properties. However, the development of a fully quantum VAE for 3D will require significant advancements in both quantum hardware and software.

vMF Latent Space

#

The heading ‘vMF Latent Space’ suggests a core methodological choice in a research paper focused on generative modeling, likely within the context of machine learning or quantum computing. The use of a von Mises-Fisher (vMF) distribution indicates the modeling of data points residing on a hypersphere, capturing directional information rather than just position. This is particularly relevant for applications where the data’s inherent structure exhibits rotational symmetry or boundedness, such as in molecular generation or other scientific domains. The ’latent’ aspect suggests this vMF distribution is embedded within a latent space of a model—perhaps a variational autoencoder (VAE)—where it acts as the prior distribution of latent variables. This choice is likely motivated by its suitability for generating data constrained to hyperspherical manifolds while avoiding the issues of unboundedness inherent to common Gaussian priors. The selection of vMF over Gaussian reveals a deep understanding of the data’s geometric properties. The results likely demonstrate improvements in data generation, especially regarding realism and diversity of generated outputs. Therefore, the paper’s likely contribution is a novel approach to generative modeling that leverages vMF distributions within the latent space for improved performance in generating data that naturally lives on a hypersphere.

NISQ-Friendly Design

#

A NISQ-friendly design in quantum machine learning focuses on creating algorithms and models that are practical for current Noisy Intermediate-Scale Quantum (NISQ) devices. This implies several crucial considerations. Reduced qubit count is paramount; NISQ devices have limited qubits, so algorithms must be efficient. Shallow circuit depth is essential to minimize the impact of noise accumulation. Hardware-efficient gates are preferred to ensure compatibility with the available gate sets. Furthermore, a hybrid approach, integrating classical and quantum computation, may be necessary for complex tasks, leveraging the strengths of both paradigms. Finally, the design should be scalable to larger systems as quantum hardware improves, making it a future-proof solution that gracefully transitions to fault-tolerant quantum computers. In summary, the core of a NISQ-friendly approach is to solve relevant problems with the limited capabilities of current hardware, minimizing noise impact while enabling progress towards more powerful quantum computation.

Conditional Generation

#

The section on ‘Conditional Generation’ would explore the ability to control the generation process of 3D molecules. Instead of producing molecules randomly, the model would be guided towards specific properties. This is achieved by incorporating condition vectors, containing desired attributes like specific atom types or desired HOMO-LUMO gaps, into the quantum circuits of both the encoder and decoder. This conditional aspect introduces a significant advancement, moving beyond purely generative methods towards a more targeted, property-specified approach to molecular design. The use of conditional qubits and layers within the quantum circuit is a key innovation, allowing for the encoding of these conditions directly into the quantum representation of the molecule, rather than relying on hybrid methods that leverage classical neural networks. The success of this approach would depend on the quantum circuit’s ability to effectively incorporate and translate the conditions into meaningful changes in the generated molecules. Experimental results should demonstrate the model’s effectiveness in generating molecules with the desired properties, showing quantitative improvements in accuracy and potentially reducing the computational burden compared to classical methods. The limitations might include challenges in scaling the number of conditions and ensuring the faithfulness of property translation within the quantum circuit.

Quantum Encoding

#

Quantum encoding, a crucial aspect of quantum machine learning, involves representing classical data as quantum states. The choice of encoding significantly impacts the efficiency and effectiveness of quantum algorithms. Amplitude encoding, for instance, offers exponential speedup in representing high-dimensional data, but requires careful normalization. Other encoding schemes like angle encoding exist, each presenting tradeoffs in qubit complexity and expressivity. In the context of molecular generation, encoding 3D coordinates, atom types, and other molecular properties requires a sophisticated approach. This often includes normalization steps to ensure the resulting quantum state adheres to the constraints of quantum mechanics. Successful encoding facilitates the subsequent quantum computations, enabling the quantum system to learn and generate new molecules. The choice of encoding method and its implementation are critical steps towards building practical and efficient quantum algorithms for molecule generation and other areas.

More visual insights

#

More on figures

This figure illustrates the process of encoding classical data of 3D molecules into a quantum state vector using amplitude encoding. The input data includes 3D coordinates and atom types. First, an auxiliary value is introduced for normalization purposes. Second, the data is normalized to have a unit norm, which is essential for amplitude encoding. Finally, this normalized data is converted into the quantum state vector via amplitude encoding. This process ensures that the data is compatible with quantum computing.

This figure shows the architecture of the quantum encoder used in QVAE-Mole and QCVAE-Mole. The encoder takes an initial quantum state as input and processes it through multiple layers consisting of single-qubit gates and entanglement gates. Each layer introduces trainable parameters. Finally, a measurement is performed on a subset of the qubits to obtain the mean direction μ in the latent space, which follows a von Mises-Fisher (vMF) distribution.

This figure shows the quantum circuit architecture of the QCVAE-Mole model, which is an extension of the QVAE-Mole model designed for conditional generation of molecules. The key difference is the inclusion of additional condition qubits and condition layers that encode specific properties into the quantum circuit. The figure illustrates how the condition qubits are used in conjunction with controlled Rx gates (CRx) to influence the state evolution of the circuit. Ultimately, the condition qubits are traced out before the output state vector is measured, reflecting the generation of a molecule with the specified properties.

This figure shows the violin plots for four molecular properties (QED, SA, LogP, and HOMO-LUMO gap) generated by QVAE-Mole (unconditional generation) and QCVAE-Mole (conditional generation). Each violin plot represents the distribution of the values for each property obtained from the generated molecules. The dashed lines in each plot indicate the target values specified as the conditions for QCVAE-Mole. The figure helps to visualize the effectiveness of the conditional generation model in controlling the desired properties of the generated molecules. The distributions’ differences between QVAE-Mole and QCVAE-Mole suggest QCVAE-Mole is able to steer the generated molecules toward the desired properties.

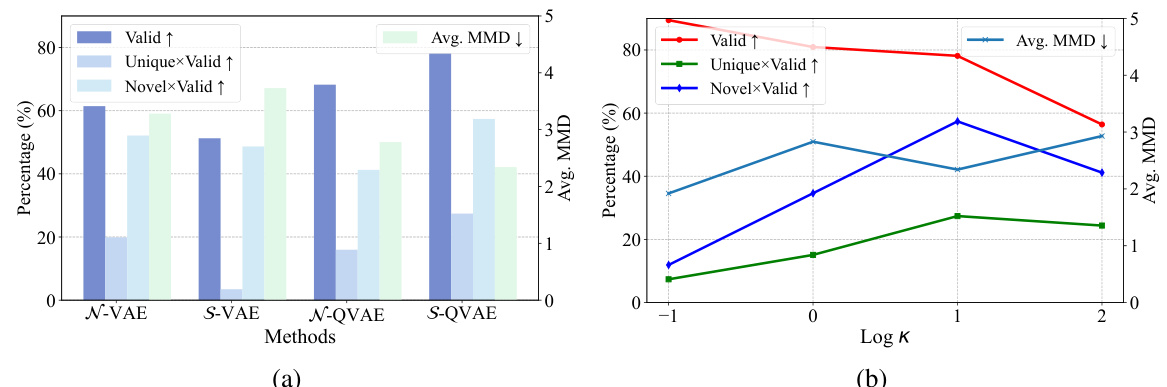
This figure compares the performance of using a normal distribution versus a von Mises-Fisher (vMF) distribution in the latent space of both classic variational autoencoders (VAEs) and the proposed quantum VAEs. Subfigure (a) shows that the vMF distribution yields better validity in the quantum VAE, highlighting its suitability for the hyperspherical structure of quantum states. Subfigure (b) explores the impact of varying the concentration parameter (κ) within the vMF distribution, demonstrating a tradeoff between the accuracy and diversity of the generated molecules.

More on tables

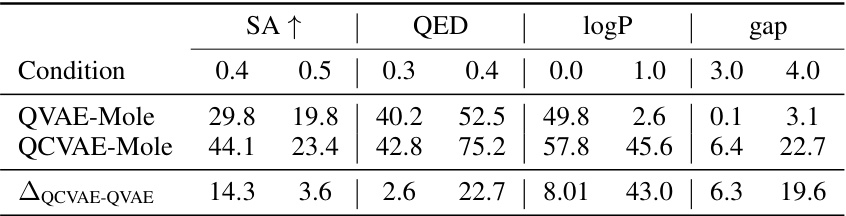
This table presents the performance of the QCVAE-Mole model under various single-condition generation tasks. For each condition (SA, QED, logP, and gap), it shows the percentage of generated molecules whose property value, after rounding, matches the specified condition. A higher percentage indicates better performance in generating molecules with the desired property. The differences between QCVAE-Mole and QVAE-Mole show the effectiveness of the conditional generation.

This table compares the performance of various methods for 3D molecule generation on the QM9 dataset. Metrics include the percentage of valid, unique, and novel molecules generated, as well as the number of classical and quantum parameters used and the inference time. The table highlights the superior performance of the proposed QVAE-Mole method in terms of quantitative results and significantly reduced parameter count.

This table compares the performance of QVAE-Mole with other state-of-the-art methods for 3D molecule generation on the QM9 benchmark dataset. Metrics include the percentage of valid, unique, and novel molecules generated, as well as the number of classical and quantum parameters and inference time. The table highlights QVAE-Mole’s competitive performance with significantly reduced parameters compared to classical counterparts and superior performance to other quantum or hybrid methods.

Full paper

#