SymILO: A Symmetry-Aware Learning Framework for Integer Linear Optimization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in optimization and machine learning because it significantly improves the accuracy of solving integer linear programs (ILPs), a common problem across various fields. The symmetry-aware approach presented offers a novel way to handle data variability inherent in symmetric ILPs, leading to more robust and efficient solutions. It opens new avenues for research in incorporating structural properties of problems into machine learning models for improved performance.

Visual Insights

#

This figure illustrates four types of permutations: identity, swapping, cyclic, and reflective. Each permutation is represented by a directed graph where nodes represent elements and edges represent mappings between elements. The identity permutation maps each element to itself. The swapping permutation swaps two elements. The cyclic permutation shifts the elements in a circular manner. The reflective permutation reverses the order of elements.

This table compares the Top-m% errors of two models, f(K) and f(K), trained using different empirical risks. The Top-m% error measures the minimum distance between predictions and the nearest equivalent solutions. Lower values indicate better performance. The table shows that the symmetry-aware model, f(K), consistently achieves lower Top-m% errors across different datasets and values of m%, demonstrating its superior solution prediction accuracy.

In-depth insights

#

Symmetry in ILPs

#

Symmetry in Integer Linear Programs (ILPs) presents a significant challenge and opportunity. Symmetry arises when permuting variables doesn’t alter the problem’s structure, leading to multiple equivalent optimal solutions. This poses problems for machine learning approaches that treat ILP solutions as labels during training because randomly selecting a single solution introduces noise and prevents the model from learning stable patterns. SymILO addresses this by integrating symmetry directly into the learning process, treating solution permutations as learnable parameters, optimized alongside model weights. This symmetry-aware approach significantly improves prediction accuracy compared to methods ignoring symmetry, demonstrating the importance of incorporating this intrinsic property into ILP solution methods.

SymILO Framework

#

The SymILO framework presents a novel approach to integer linear programming (ILP) by integrating machine learning and symmetry awareness. SymILO directly addresses the challenge of label variability in training data caused by ILP symmetry, where multiple optimal solutions exist. By incorporating solution permutation as a learnable parameter alongside neural network weights, SymILO learns stable patterns regardless of the specific optimal solution selected as a label during training. This symmetry-aware approach significantly improves prediction accuracy, outperforming existing methods across diverse ILP benchmarks involving different symmetry types. The framework’s alternating optimization algorithm efficiently handles the discrete nature of permutation operations, making it a computationally viable solution for a range of practical applications. The effectiveness across different downstream tasks, further highlights the robustness and versatility of the SymILO framework.

Alternating Minimization

#

Alternating minimization is a powerful optimization technique particularly well-suited for problems involving both continuous and discrete variables, as demonstrated in the context of the symmetry-aware learning framework for integer linear programs (ILPs). The core idea is to iteratively optimize one set of variables while holding the others fixed, cycling between continuous model parameters and discrete permutation operators. This approach cleverly addresses the challenge posed by ILP symmetries where multiple optimal solutions exist, significantly enhancing the model’s ability to learn stable patterns. By alternating optimization, the algorithm avoids simultaneously handling both continuous and discrete variables, simplifying the optimization process and improving efficiency. The effectiveness of this strategy is supported by experimental results showcasing significant improvements over existing methods, highlighting the power of incorporating inherent problem structure into the optimization strategy. The careful design of the alternating steps, particularly the sub-problem solving for various symmetry groups, further underscores the framework’s sophistication and adaptability. Overall, alternating minimization proves to be a crucial component of the proposed framework, leading to a considerable performance boost by effectively leveraging the problem’s symmetry.

Downstream Tasks

#

The ‘Downstream Tasks’ section of this research paper is crucial because it evaluates the effectiveness of the proposed SymILO framework’s predictions in real-world scenarios. Instead of solely focusing on prediction accuracy, the authors integrate three distinct downstream tasks—fix and optimize, local branching, and node selection—to gauge the impact of SymILO’s output on the actual solution process. This multi-faceted approach provides a more comprehensive assessment. The inclusion of established baselines for each downstream task (ND, PS, and MIP-GNN) allows for a direct comparison, highlighting SymILO’s improvements. The use of metrics like relative primal gap, alongside Top-m% error, further strengthens the evaluation by examining solution quality in a practical context. This methodology showcases a thorough investigation of SymILO’s applicability and efficacy, beyond just prediction accuracy.

Future Research

#

Future research directions stemming from this work could explore several promising avenues. Extending SymILO to handle more complex symmetry groups beyond those currently addressed (symmetric, cyclic, dihedral) is crucial for broader applicability. Developing more efficient optimization algorithms within the alternating minimization framework is necessary to mitigate computational costs, particularly for large-scale problems. Investigating the impact of different neural network architectures and loss functions on the performance of SymILO warrants further investigation. Finally, a comprehensive empirical comparison against a wider range of existing ILP solvers and symmetry-handling techniques would strengthen the conclusions and provide a more complete picture of SymILO’s effectiveness.

More visual insights

#

More on figures

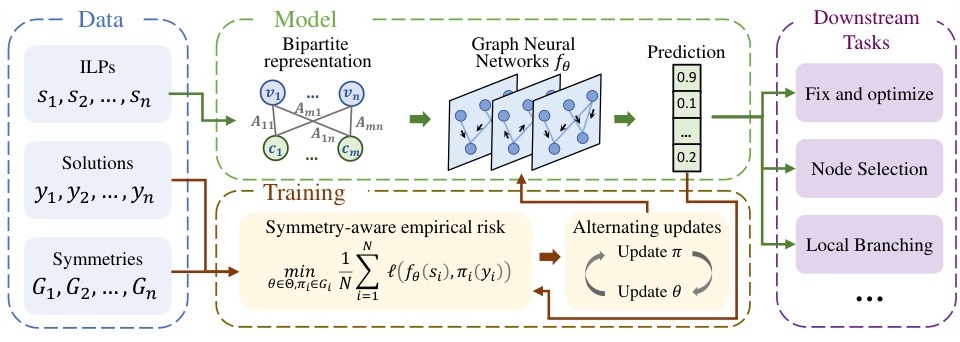
This figure presents a schematic overview of the SymILO framework. It illustrates the data flow, processing stages, and key components involved in training a symmetry-aware model for integer linear program (ILP) solution prediction. The framework consists of three main stages: data processing (including the input ILPs, their optimal solutions, and their symmetry groups), model training (using a graph neural network and an alternating optimization algorithm that leverages the ILP’s symmetry), and downstream tasks (where the model predictions are used by different algorithms to find feasible solutions). The figure highlights how symmetry information is incorporated into both the training process and the subsequent downstream tasks to improve the quality of the predictions.

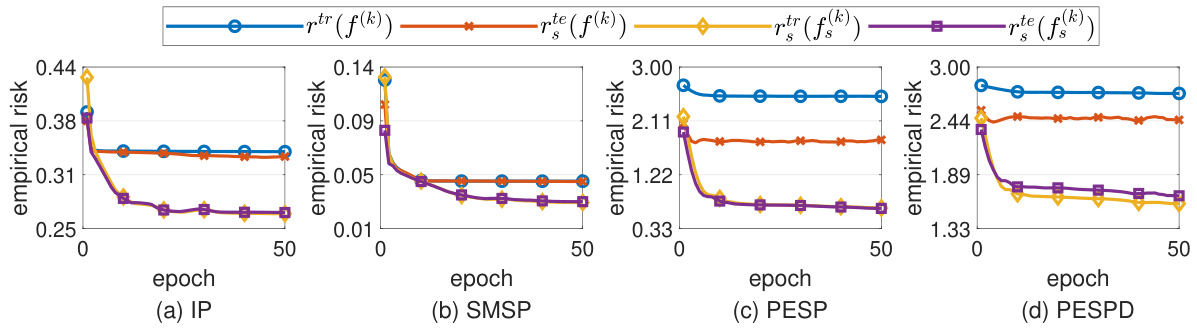
This figure displays the training and testing empirical risks plotted against the number of epochs for four different benchmark problems (IP, SMSP, PESP, and PESPD). The plot shows the training and testing risks for both the classic model and the symmetry-aware model. The results demonstrate that the symmetry-aware model consistently achieves lower empirical risks compared to the classic model after training convergence, supporting the effectiveness of the proposed symmetry-aware approach.

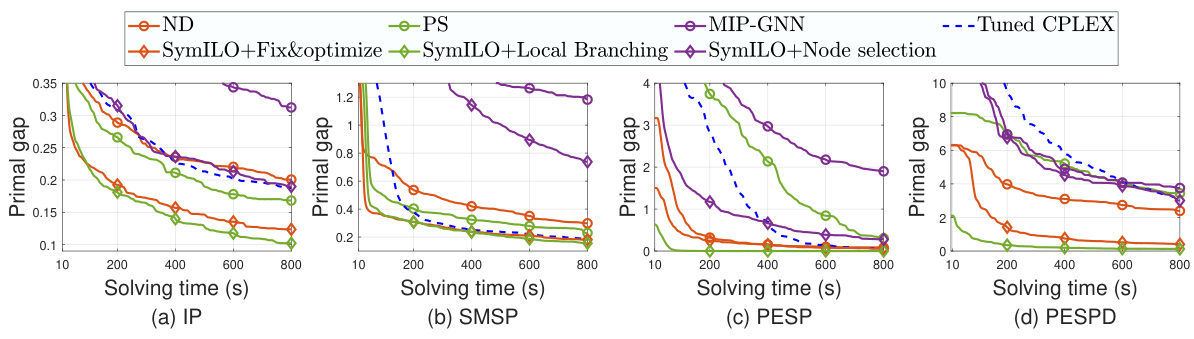
This figure shows the relative primal gaps achieved by different downstream tasks (fix-and-optimize, local branching, node selection) at various time points up to 800 seconds. Each downstream task uses a specific color, allowing for easy comparison. The performance of a tuned CPLEX solver (single-thread) is included as a baseline (blue dashed line). The figure illustrates how the SymILO framework improves the primal gap across all downstream tasks compared to the baseline methods.

This figure illustrates equivalent solutions to the bin packing problem (Example B.0.1) presented earlier in the paper. Since all bins are identical, swapping them does not change the feasibility or the objective value. The figure visually demonstrates how different arrangements of items within the bins represent equivalent solutions to the optimization problem. The key takeaway is that the symmetry of the problem (identical bins) leads to multiple equivalent solutions.

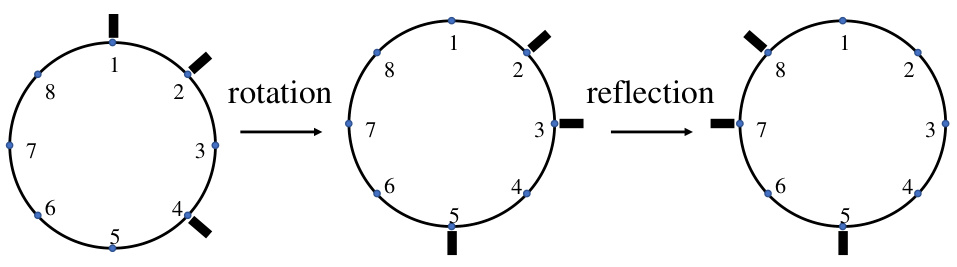
This figure illustrates equivalent solutions for Example B.0.2, a problem involving placing ticks on a circle such that distances between ticks are distinct. The leftmost circle shows an initial solution. The middle circle demonstrates a rotation of the ticks, resulting in an equivalent solution because distances remain unchanged. The rightmost circle shows a reflection of the ticks, again producing an equivalent solution due to preserved distances. This highlights the concept of symmetry in the problem, where certain permutations of solutions yield the same objective value.

More on tables

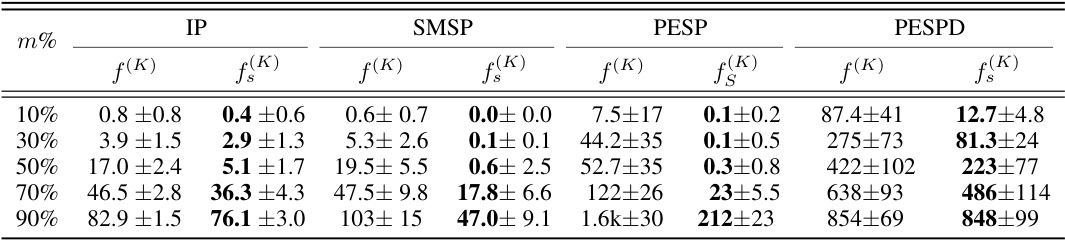
This table compares the Top-m% errors of the models trained using the classic empirical risk (f(K)) and the symmetry-aware empirical risk (f(K)). Top-m% error is defined as the sum of the absolute differences between rounded prediction values and their closest equivalent solution values for the top m% of variables with the largest difference between the rounded prediction and actual values. Lower values indicate better performance. The results are averaged across four different datasets: IP, SMSP, PESP, and PESPD, each with varying levels of symmetry. The table demonstrates that the symmetry-aware approach consistently achieves lower Top-m% errors compared to the classic approach for all m% values across all datasets, highlighting its improved performance.

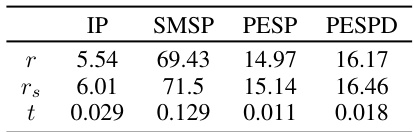
This table shows the time taken to minimize the empirical risk (r) and the symmetry-aware empirical risk (rs) for each dataset. The column ’t’ represents the average time spent solving the permutation decisions per instance during the minimization of rs. It demonstrates that the proposed alternating optimization algorithm (SymILO) for updating model parameters and permutation operations is computationally efficient, with the added step of updating permutations in the rs minimization not significantly increasing the overall time.

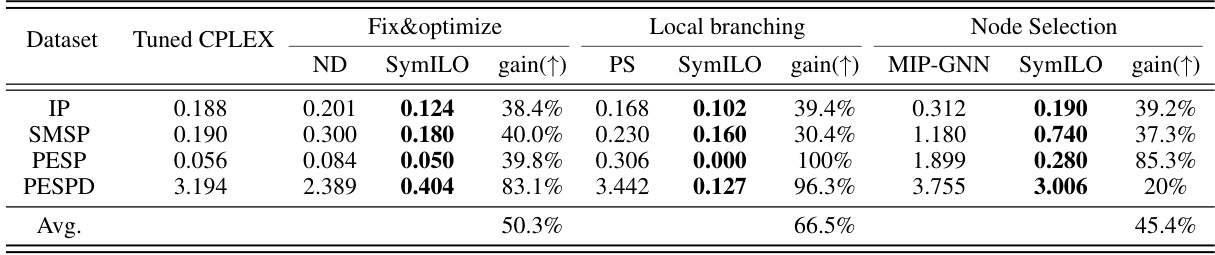
This table presents the average relative primal gaps achieved by different methods across four benchmark datasets, for three different downstream tasks: fix and optimize, local branching, and node selection. The ‘gain’ column shows the percentage improvement of SymILO over the baseline methods for each task and dataset. Tuned CPLEX serves as a reference point representing the performance of a well-tuned commercial solver.

This table shows the hyperparameters used for the three downstream tasks (fix and optimize, local branching, and node selection) for each dataset (IP, SMSP, PESP, PESPD). The hyperparameters α and β are tuned for both the classic empirical risk (r) and the symmetry-aware empirical risk (rs) approaches. The values indicate the optimal settings found for each configuration.

This table presents the Top-m% errors for different values of m (10%, 30%, 50%, 70%, 90%) achieved by the classic model f(K) and the symmetry-aware model f(K). Lower values indicate better performance. The results are averaged across four different datasets: IP, SMSP, PESP, and PESPD. This comparison shows how using symmetry awareness improves the prediction accuracy.

This table presents the average relative primal gaps achieved by three different downstream tasks (fix-and-optimize, local branching, node selection) at 800 seconds of solving time. It compares the performance of SymILO against three baselines (ND, PS, MIP-GNN) and tuned CPLEX. The relative primal gap is a metric that measures the relative difference between the objective value of a feasible solution obtained and the optimal solution’s objective value. Lower values indicate better performance. The table also shows the percentage gain achieved by SymILO compared to each baseline.

Full paper

#