↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world applications deal with incomplete spatio-temporal data, leading to challenges in analysis and prediction. Existing methods often rely on iterative message-passing across spatial and temporal dimensions, but these approaches are susceptible to information loss and high computational costs, particularly with highly sparse data. These limitations are theoretically analyzed in the paper, showing the susceptibility of iterative methods to sparsity.
The paper proposes a novel method, OPCR (One-step Propagation and Confidence-based Refinement), that directly addresses these issues. OPCR uses a sparse attention mechanism for one-step imputation, followed by a confidence-based refinement step to integrate spatial and temporal information. This approach significantly improves accuracy and reduces computational cost compared to iterative methods. Empirical evaluations demonstrate the superiority of OPCR across various downstream tasks involving highly sparse spatio-temporal datasets, highlighting its effectiveness and robustness.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the critical issue of handling highly sparse spatio-temporal data, a common challenge in many real-world applications. The proposed method, OPCR, offers a significant improvement over existing techniques by achieving better accuracy and efficiency, opening new avenues for research and application in diverse fields.
Visual Insights#

This figure illustrates the framework of the proposed One-step Propagation and Confidence-based Refinement (OPCR) method. It shows a two-stage process. The first stage involves independent learning of spatial and temporal representations for spatio-temporal points using sparse attention mechanisms. These representations are then used for one-step imputation of missing data. The second stage refines the imputation results by assigning confidence levels based on correlations between data points and then performing weighted spatio-temporal propagation to address potential biases. The figure visually represents the flow of information through the model, highlighting the key components such as input data, sparse attention modules, imputation steps, confidence-based refinement, and final predictions.

This table presents the key statistics of the three datasets used in the paper’s experiments: TRAFFIC, LARGE-SCALE, and T4C22. For each dataset, it shows the number of nodes, edges, and time steps. The TRAFFIC dataset includes PEMS-BAY and METR-LA. The LARGE-SCALE dataset includes PV-US, CER-E, LONDON, MADRID. The T4C22 dataset includes LONDON, MADRID, MELBOURNE. This information is crucial for understanding the scale and characteristics of the data used to evaluate the proposed spatio-temporal imputation method.
In-depth insights#
Sparse Data Imputation#
Sparse data imputation, a crucial aspect of handling incomplete spatio-temporal data, is addressed by the paper. The authors highlight the limitations of iterative methods, which are susceptible to information loss and instability due to data and graph sparsity. They propose a novel one-step propagation and confidence-based refinement (OPCR) method to overcome these limitations. OPCR leverages inherent spatial and temporal relationships through a sparse attention mechanism, directly propagating limited observations to the global context for a more robust imputation. A key innovation is the assignment of confidence levels to initial imputations, which allows the refinement of the results through spatio-temporal dependencies. The effectiveness of the approach is demonstrated through experiments showcasing superior performance compared to existing imputation methods across various downstream tasks involving highly sparse data. The theoretical analysis provided gives insights into the limitations of traditional iterative models. Overall, the paper presents a significant improvement in dealing with sparse spatio-temporal data imputation, offering both theoretical justification and empirical evidence for its effectiveness.
One-Step Propagation#
The concept of “One-Step Propagation” in the context of spatiotemporal data imputation presents a compelling alternative to traditional iterative methods. Its core strength lies in directly propagating information from observed data points to missing ones in a single step, bypassing the iterative refinement process inherent in many existing techniques. This approach not only significantly reduces computational costs but also mitigates the risk of information loss and error accumulation associated with multiple iterations. The efficacy of one-step propagation hinges on the capability of the underlying model to effectively capture and leverage inherent spatial and temporal dependencies. Techniques like sparse attention mechanisms are well-suited for this task, enabling efficient information flow even with highly sparse data. While the one-step approach might not achieve the same level of refinement as iterative methods in some instances, its efficiency and robustness make it particularly attractive for large-scale datasets where computational constraints are paramount. The trade-off between computational efficiency and imputation accuracy is a critical aspect to consider when evaluating the effectiveness of one-step propagation in a specific application. Further research could focus on exploring more sophisticated attention mechanisms or incorporating additional contextual information to improve the accuracy of one-step imputation.
Confidence Refinement#
Confidence refinement, in the context of spatio-temporal data imputation, is a crucial step to enhance the accuracy and robustness of predictions. It acknowledges that initial imputation methods, even sophisticated ones like sparse attention mechanisms, may introduce biases or uncertainties. By correlating missing data with valid observations and leveraging spatio-temporal dependencies, a confidence score is assigned to each imputed value. Higher confidence scores signify greater reliability, enabling a weighted combination of spatial and temporal imputation results. This refinement stage effectively mitigates the inherent uncertainties associated with single imputation methods, leading to more accurate and balanced final predictions. It is a key aspect of achieving a more resilient and reliable system. The process of assigning confidence scores requires careful consideration of the correlation structure within the data, choosing appropriate correlation measures, and potentially using advanced techniques such as probabilistic modeling. The effectiveness of confidence refinement is directly tied to the quality and informativeness of the available data. Therefore, a comprehensive approach that includes techniques to handle noisy or incomplete data during confidence assignment is paramount for optimal results. The final step involves a weighted spatio-temporal propagation, improving the global coherence of the imputed data. This is an area for further research: exploring more advanced techniques to improve confidence estimation and incorporate external knowledge or domain-specific information to further enhance the imputation process.
PAC-Learnability Analysis#
A PAC-learnability analysis for spatio-temporal imputation would rigorously examine the theoretical guarantees of learning algorithms under sparsity. It would likely involve defining a concept class representing the imputation models, then proving that, with enough data, the algorithm can learn a model that is both accurate and generalizes well to unseen data. Key challenges would include handling the inherent complexities of spatio-temporal data, such as the dependencies between spatial locations and temporal instances. The analysis would probably highlight the impact of sparsity, showing how the learnability of imputation models degrades as the data becomes increasingly sparse. This is crucial because existing iterative methods are shown to suffer from information loss and instability under sparsity, hence the exploration of alternative one-step imputation methods is justified. The analysis might also investigate how model complexity, as measured by measures like VC-dimension or Rademacher complexity, affects learnability. Ultimately, a successful PAC-learnability analysis would provide strong theoretical justification for the proposed one-step approach, offering a theoretical underpinning for its empirical performance advantages.
Future Directions#
Future research could explore extending the model’s capabilities to handle more complex spatio-temporal patterns and higher dimensional data. Improving the model’s scalability to efficiently process massive datasets is crucial for real-world applications. Investigating alternative attention mechanisms and exploring different imputation strategies could potentially enhance the model’s accuracy and robustness. A deeper theoretical understanding of the model’s behavior under various data sparsity levels and noise conditions is also needed. Furthermore, research into handling different types of missing data mechanisms beyond point-level and node-level missing is warranted. Finally, exploring the application of OPCR to diverse domains and evaluating its performance on various downstream tasks will further demonstrate its generalizability and practical value.
More visual insights#
More on figures

This figure displays the Mean Absolute Error (MAE) for imputation on four different datasets (PEMS-BAY, METR-LA, PV-US, and CER-E) across various missing rates (25%, 50%, 75%, 95%). It compares the performance of the proposed OPCR model against several baseline methods (PriSTI, IGNNK, BRITS, SPIN-H, and SAITS). The graph allows for a visual comparison of the different imputation methods’ robustness to increasing data sparsity in point-level missing scenarios.

This figure displays the Mean Absolute Error (MAE) for imputation across four different datasets (PEMS-BAY, METR-LA, PV-US, and CER-E) at various missing rates (25%, 50%, 75%, 95%). The performance of six different imputation methods (OPCR, PriSTI, IGNNK, SPIN-H, BRITS, and SAITS) is compared, showing how their MAE changes with increasing spatial data sparsity. The results highlight the relative performance of each imputation method under different levels of missing spatial data.

This figure illustrates the framework of the One-step Propagation and Confidence-based Refinement (OPCR) model. The model consists of two main stages. The first stage involves independent learning of spatial and temporal representations for spatio-temporal points using sparse attention mechanisms. These separate representations are then used for one-step imputation to directly propagate information from observed to missing data points. The second stage assigns confidence levels to these initial imputations by correlating missing and valid data points, and refines these imputations through spatio-temporal dependencies using a weighted propagation method. This framework is designed to handle highly sparse spatio-temporal data efficiently and accurately by avoiding the error accumulation and information loss often associated with iterative imputation methods.
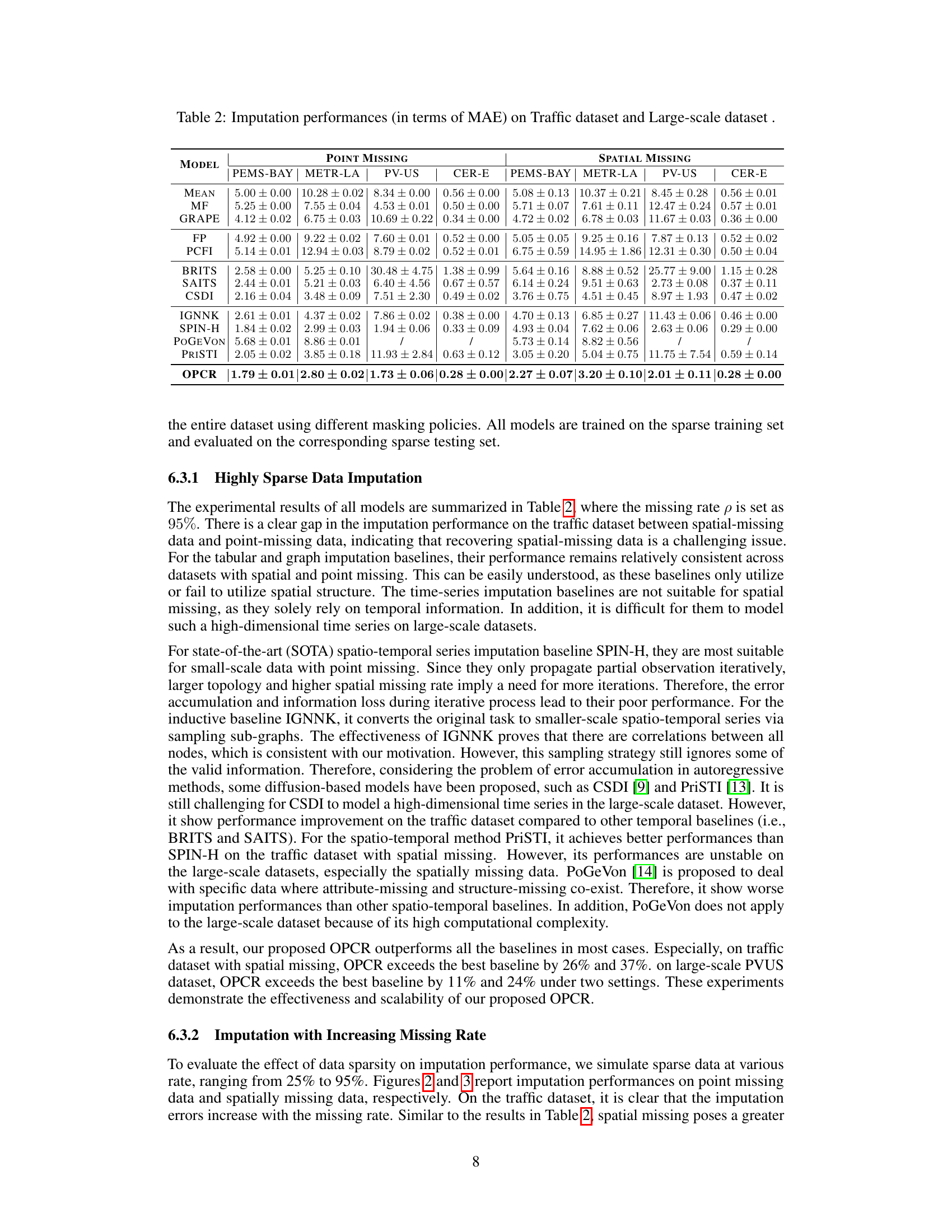
This figure displays the results of an ablation study, evaluating the impact of different components on the model’s performance. The left panel shows the performance impact by changing the size of hidden layers in both the spatial and temporal modules, for datasets with point and spatial missing data. The right panel shows the results of varying the number of layers in the refinement stage of the model, also for datasets with point and spatial missing data. The results help demonstrate the contribution of each component (spatial module, temporal module, and refinement) to the overall imputation performance.
More on tables
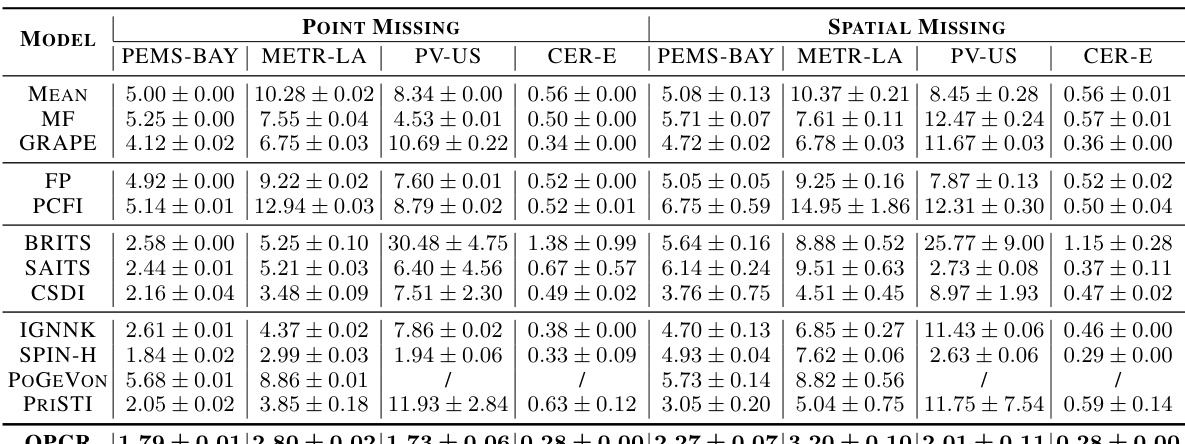
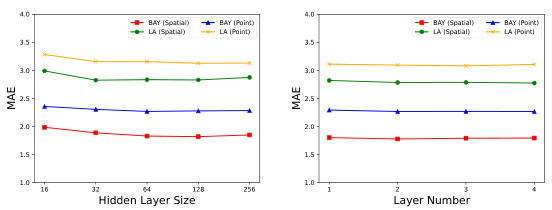
This table presents the Mean Absolute Error (MAE) achieved by different imputation methods on two datasets: Traffic and Large-scale. It compares the performance across various methods (Mean, MF, GRAPE, FP, PCFI, BRITS, SAITS, CSDI, IGNNK, SPIN-H, PoGeVon, PriSTI, and OPCR) under two missing data scenarios: point missing and spatial missing. The results show the MAE for each method on four different subsets within each dataset (PEMS-BAY, METR-LA, PV-US, and CER-E).
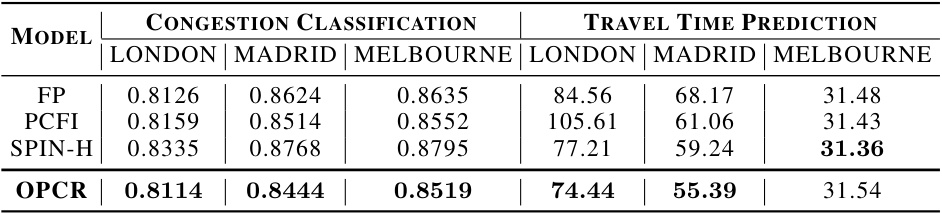
This table presents the performance comparison of different models on two downstream tasks of the T4C22 dataset: congestion classification and travel time prediction. The metrics used are weighted cross-entropy loss for congestion classification and MAE for travel time prediction. The results show the performance of each model across three cities: London, Madrid, and Melbourne.
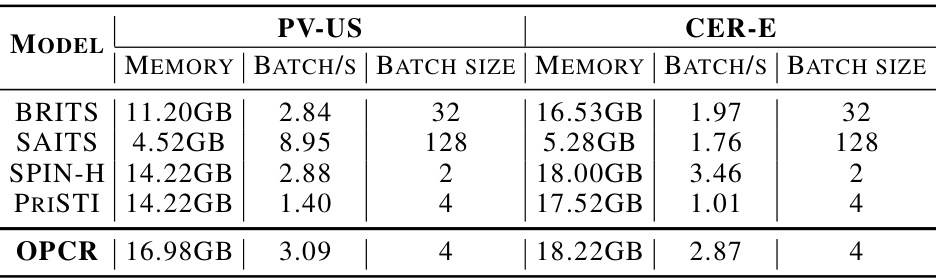
This table shows the memory consumption and training speed (in terms of batches per second) for various models on two large-scale datasets (PV-US and CER-E). The results demonstrate that the proposed OPCR model is computationally efficient and has significant advantages over other state-of-the-art imputation methods.
Full paper#