↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline reinforcement learning (RL) shows promise for applications where real-time data collection is difficult, but real-world offline datasets often contain various corruptions (noise, errors, adversarial attacks). Existing offline RL methods struggle to learn robust agents under such uncertainty, leading to performance drops in clean environments. This necessitates robust methods that can handle diverse data corruptions effectively.
The paper introduces TRACER, a novel robust variational Bayesian inference method for offline RL. TRACER models all types of corruptions as uncertainty within the action-value function. It utilizes all available offline data to approximate the posterior distribution of this function using Bayesian inference. A key feature is its entropy-based uncertainty measure, allowing TRACER to differentiate corrupted data from clean data and reduce the influence of unreliable data points. This approach enhances the algorithm’s robustness and improves its performance in clean environments. Experiments demonstrate significant performance improvements over state-of-the-art methods in various corruption scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in offline reinforcement learning (RL) and related fields because it tackles the critical problem of robustness against diverse data corruptions, a common issue in real-world applications. The proposed TRACER method offers a novel solution by integrating Bayesian inference to effectively manage uncertainty in offline data, significantly improving performance in clean environments. This opens exciting new avenues for developing more robust and reliable RL algorithms for diverse applications, including healthcare and autonomous driving.
Visual Insights#
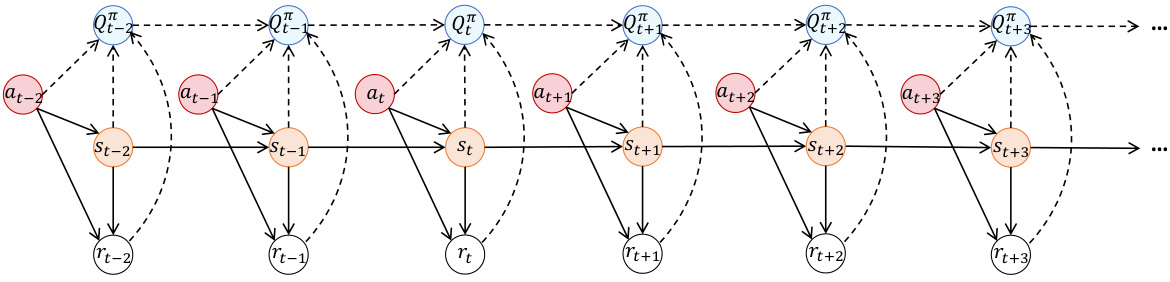
This figure shows a graphical model representing the decision-making process in reinforcement learning. The solid lines connect observed data points present in the offline dataset (states, actions, rewards, next states). The dashed lines represent the unobserved Q-values (action-values), which are the target variables offline RL algorithms aim to estimate. The figure highlights that while the offline dataset provides some data, the Q-values are inferred based on the observed data and their correlations.

This table presents the average performance scores and standard errors of different offline reinforcement learning algorithms under different corruption scenarios. The algorithms are evaluated on three MuJoCo environments (HalfCheetah, Walker2d, and Hopper). Each environment is tested under random and adversarial simultaneous corruption, meaning both types of corruption are applied simultaneously. The table allows for a comparison of algorithm robustness to diverse forms of data corruption.
In-depth insights#
Robust Offline RL#
Robust Offline Reinforcement Learning (RL) tackles the challenge of training effective agents using only a fixed dataset, without the ability to interact with the environment. This is crucial for scenarios where data collection is expensive or dangerous. A core issue is distribution shift, where the data used for training doesn’t accurately represent the environment the agent will ultimately operate in. Robust methods focus on mitigating this by incorporating techniques to handle uncertainty, such as Bayesian inference or ensemble methods. They also strive to improve generalization to unseen situations and reduce sensitivity to data corruption (noise or adversarial attacks), thus enhancing the reliability and performance of the learned policy in real-world deployments.
Bayesian Inference#
Bayesian inference, in the context of offline reinforcement learning (RL), offers a robust approach to handle uncertainties stemming from diverse data corruptions. Instead of relying on point estimates, Bayesian methods model the uncertainty inherent in the action-value function, capturing uncertainty from noisy or adversarial data. This approach is particularly valuable in offline RL settings because direct interaction with the environment for data collection is often impossible. By treating the action-value function as a probability distribution rather than a single value, Bayesian inference provides a more nuanced understanding of the environment, leading to more robust and reliable policy learning. The incorporation of Bayesian inference allows for principled methods to distinguish clean data from corrupted data, thus leading to improved performance on clean data. A major advantage is that it directly addresses uncertainty across all aspects of the data (states, actions, rewards, and dynamics), unlike methods only focusing on a subset of them.
Entropy-based Measure#
The concept of an ‘Entropy-based Measure’ in the context of robust offline reinforcement learning (RL) offers a novel approach to handling data corruptions. The core idea revolves around the observation that corrupted data points tend to exhibit higher uncertainty and consequently, higher entropy than their clean counterparts in the action-value function distribution. This distinction forms the basis for a mechanism to effectively identify and downweight the influence of corrupted data during training. By quantifying the entropy associated with each data point, the algorithm can assign weights that reduce the contribution of uncertain observations to the overall learning process. This strategy is particularly useful in offline RL where direct interaction with the environment is limited, and the dataset might contain various types of noise or adversarial perturbations. The use of an entropy-based measure enables a more nuanced approach to data filtering compared to simply discarding data points based on heuristics, thus improving the robustness and accuracy of the learned policy.
Diverse Data Tests#
A robust offline reinforcement learning model should ideally perform well under diverse data conditions. A section titled “Diverse Data Tests” would be crucial for validating such a model’s generalizability and robustness. These tests would encompass various types of data corruptions, including random noise, adversarial attacks, and missing data, affecting states, actions, rewards, or dynamics. The testing methodology would involve evaluating the model’s performance across different corruption levels (e.g., varying the noise magnitude or the percentage of corrupted data). This comprehensive testing strategy would provide a thorough assessment of the model’s ability to handle real-world scenarios where data imperfections are common. Quantitative metrics such as average return, success rate, and stability would be essential for a comprehensive evaluation. The results would demonstrate not only the model’s resilience but also highlight its strengths and weaknesses under different types of data corruptions, ultimately contributing to building a more reliable and robust model. The section should also detail the types of data sets used and whether the testing was performed on datasets created from the same distribution as the training dataset to test for generalization and overfitting issues.
Future Work#
Future research directions stemming from this work on robust offline reinforcement learning could explore several key areas. Extending TRACER to handle even more complex data corruptions, such as those involving intricate correlations between different data elements or time-varying corruptions, would enhance its real-world applicability. Investigating the theoretical limits of TRACER’s robustness under diverse corruption scenarios is crucial, potentially involving a more nuanced understanding of the Wasserstein distance’s limitations in capturing complex uncertainty. Improving efficiency is another important direction; exploring alternative inference techniques or approximate Bayesian methods could potentially accelerate the learning process. Finally, applying TRACER to a broader array of tasks and environments, including real-world applications in robotics or autonomous systems, would demonstrate its practical value and uncover potential limitations in diverse contexts.
More visual insights#
More on figures
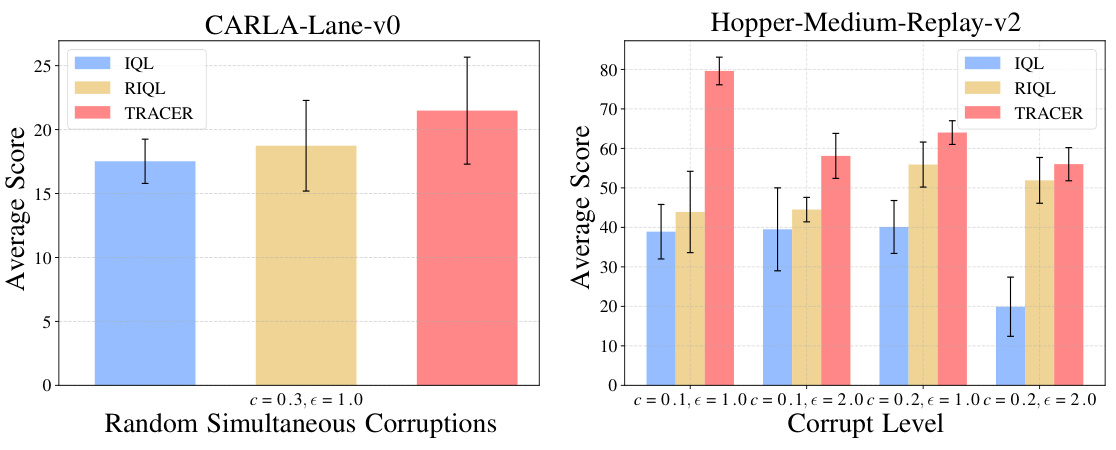
This figure shows the performance of different offline reinforcement learning algorithms under random simultaneous data corruptions. The left panel shows the average scores and standard deviations on the CARLA environment with corruption rate c = 0.3 and scale = 1.0. The right panel shows how the performance changes at different corruption levels (varying c and epsilon) in the Hopper environment.
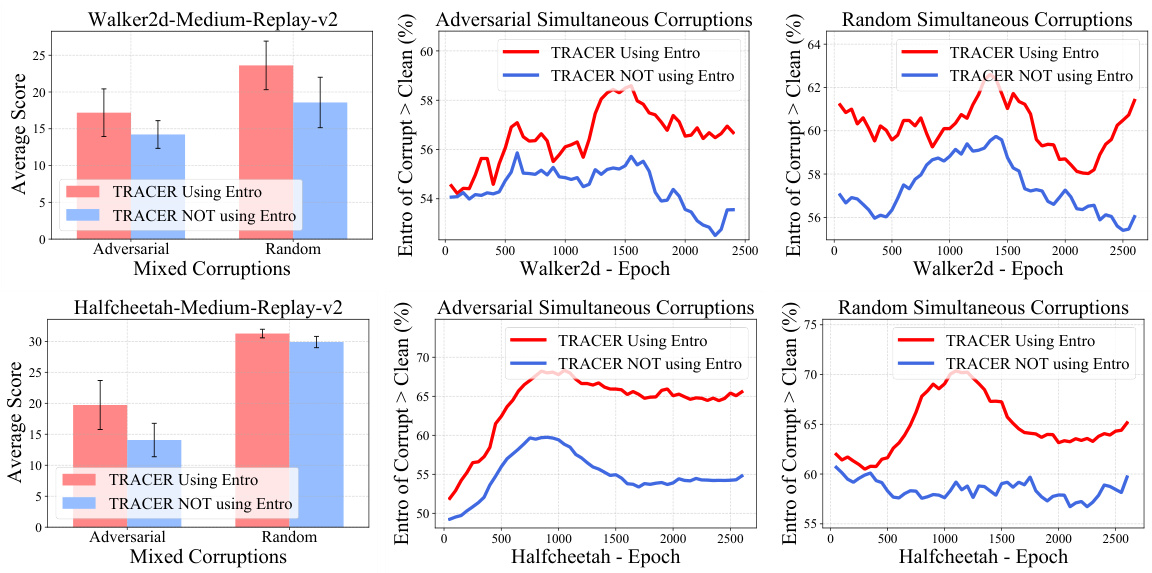
This figure presents results from experiments comparing TRACER’s performance with and without using an entropy-based uncertainty measure. The leftmost column shows average performance across different corruption types. The remaining two columns illustrate the entropy difference between clean and corrupted data throughout training, demonstrating how the entropy-based measure effectively distinguishes between the two.

This figure shows the architecture of the TRACER model. It consists of four main components: an ensemble of observation models that model the uncertainty in states, actions, rewards and next states; a critic network that uses quantile regression to approximate the action-value distribution and value function; a value network; and an actor network that outputs the policy. The figure highlights how the ensemble models and the critic network interact and how the resulting action-value distribution is used to update the actor network’s policy.
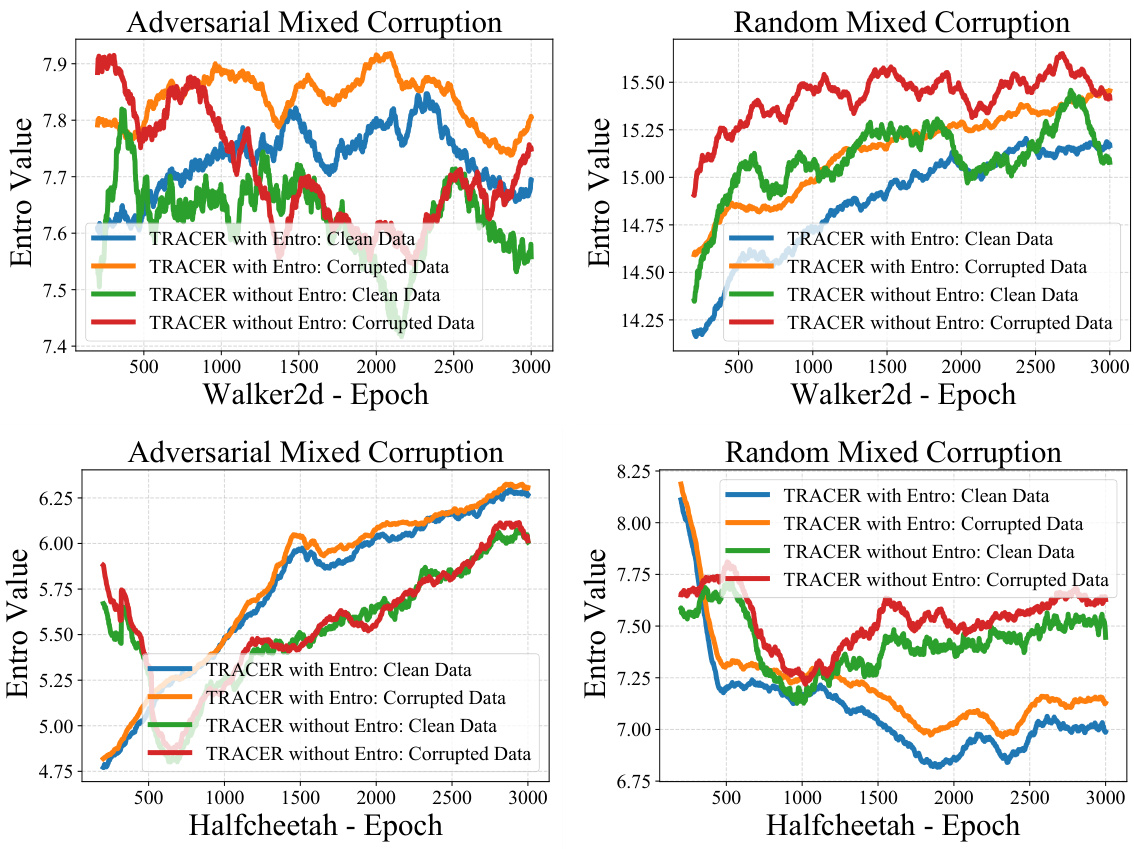
This figure shows the results of using entropy-based uncertainty measure in TRACER. The first column compares the performance of TRACER with and without the entropy-based uncertainty measure. The second and third columns show the entropy of clean and corrupted data over training epochs for two different environments.
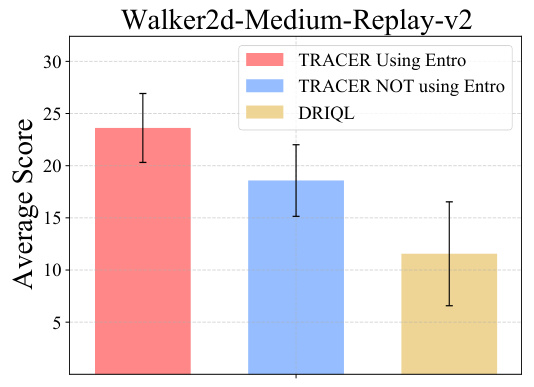
This figure compares the performance of TRACER with and without the entropy-based uncertainty measure. The first column shows the average entropy of corrupted data is higher than clean data using TRACER. The second and third columns demonstrate this higher entropy of corrupted versus clean data over training epochs in two different MuJoCo tasks.
More on tables

This table presents the average performance scores and their standard errors for different reinforcement learning algorithms across various environments (Halfcheetah, Walker2d, Hopper) under different corruption scenarios. The corruption scenarios involve simultaneous random and adversarial corruptions of observations, actions, rewards, and dynamics in the offline datasets. The table allows for a comparison of the robustness of different algorithms against various data corruptions. TRACER (ours) consistently outperforms other algorithms across all environments and corruption types.

This table presents the average performance scores of different offline reinforcement learning algorithms under various adversarial corruptions. The algorithms are evaluated on three different environments (Halfcheetah, Walker2d, and Hopper) with corruptions applied to different elements of the dataset (observation, action, reward, and dynamics). The table shows TRACER significantly outperforms other algorithms across all environments and corruption types.

This table presents the average performance scores and standard errors of different offline reinforcement learning algorithms under conditions of simultaneous random and adversarial data corruptions. The algorithms are evaluated across three different MuJoCo environments (Halfcheetah, Walker2d, and Hopper). The results show the average performance across both random and adversarial corruptions, offering a comparison of algorithm robustness. The table helps illustrate the performance advantage of the proposed TRACER algorithm in handling diverse data corruptions.
This table presents the average scores and standard errors achieved by various offline reinforcement learning algorithms on three different environments (Halfcheetah, Walker2d, and Hopper) under simultaneous random and adversarial corruptions. The results are compared across different corruption methods and show the performance differences between the algorithms in handling diverse data corruption scenarios. The results highlight the impact of the various algorithms and their handling of noisy data.

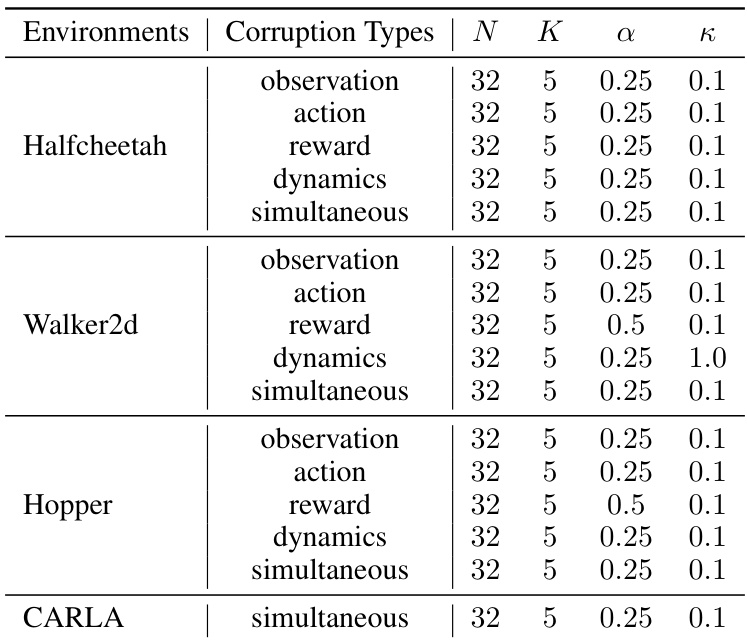
This table lists the hyperparameters used in the TRACER algorithm for the random corruption benchmark. It specifies the number of samples (N), number of ensemble models (K), and alpha and kappa values for each environment (Halfcheetah, Walker2d, Hopper) and corruption type (observation, action, reward, dynamics, simultaneous). These hyperparameters control the model’s behavior and learning process under different corruption scenarios.

This table presents the average performance and standard errors of TRACER on the Hopper-medium-replay-v2 task, focusing on hyperparameter tuning. It shows the results under four different types of corruptions (Random Dynamics with κ values of 0.01, 0.1, 0.5, and 1.0; Adversarial Reward with the same κ values). The table is meant to illustrate the impact of the hyperparameter κ (a threshold parameter in the Huber loss function) on the model’s robustness under various corruption scenarios, showing how different settings influence the average performance. The bold values highlight the best-performing hyperparameter setting.

This table presents the average performance and standard errors of RIQL and TRACER (with and without entropy-based uncertainty measure) under various individual corruptions in the Hopper-medium-replay-v2 environment. The results are averaged over two seeds and using 64 batch sizes. It showcases the performance difference in each individual corruption type (observation, action, reward, dynamics) for both random and adversarial corruptions. The
TRACER (New)row indicates an improved version of TRACER.

This table presents the average scores and standard errors achieved by IQL, RIQL, and TRACER on four different benchmark tasks (AntMaze-Medium-Play-v2, AntMaze-Medium-Diverse-v2, Walker2d-Medium-Expert-v2, and Hopper-Medium-Expert-v2) under random simultaneous corruptions. The results demonstrate TRACER’s superior performance compared to the baseline methods, showcasing its effectiveness in handling simultaneous corruptions across various environments.

This table presents the average scores and standard errors obtained by RIQL and TRACER (the proposed method) on the Hopper-medium-replay-v2 task under different levels of random simultaneous data corruption. The corruption level is controlled by the
corrupt rate c, with values ranging from 0.1 to 0.5, which correspond to approximately 34.4%, 59.0%, 76.0%, 87.0%, and 93.8% of corrupted data, respectively. The table demonstrates TRACER’s robustness against data corruption and highlights its superior performance compared to RIQL, especially at higher corruption levels.

This table presents the average performance scores and standard errors of various offline reinforcement learning algorithms under conditions of simultaneous random and adversarial data corruptions. The results are categorized by environment (Halfcheetah, Walker2d, Hopper), type of corruption (random or adversarial), and algorithm (BC, EDAC, MSG, UWMSG, CQL, IQL, RIQL, TRACER). The table highlights the relative performance of each algorithm when dealing with corrupted data.
Full paper#



















