Learning to Balance Altruism and Self-interest Based on Empathy in Mixed-Motive Games

ry0RXTJwjy

Fanqi Kong et el.

TL;DR
#

Many real-world scenarios involve mixed motives, requiring AI agents to cooperate while protecting themselves. Existing approaches struggle to achieve both. This is a significant problem because purely selfish agents can exploit altruistic ones, while overly altruistic agents may be taken advantage of. There is a need for AI agents that can dynamically balance these competing goals.

The paper introduces LASE (Learning to balance Altruism and Self-interest based on Empathy), a novel algorithm that addresses this challenge. LASE uses a counterfactual reasoning approach and a perspective-taking module to infer social relationships, and then uses this to guide its gifting strategy—sharing rewards with helpful teammates while minimizing exploitation. Extensive experiments show LASE’s success in various games, demonstrating its ability to promote cooperation without compromising fairness or self-protection.

Key Takeaways
#

Why does it matter?
#

This paper is important because it presents LASE, a novel algorithm that tackles a critical challenge in multi-agent reinforcement learning: balancing altruism and self-interest in mixed-motive games. It offers a computational model of empathy to guide decision-making, addressing limitations of existing methods. This work opens avenues for creating more sophisticated, human-like AI agents capable of navigating complex real-world interactions. The insights and techniques are relevant to various fields beyond AI, including economics and social sciences.

Visual Insights
#

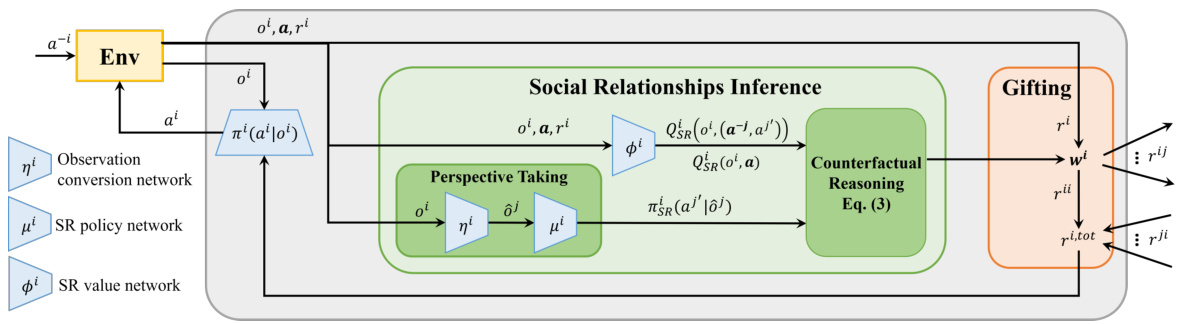
The figure illustrates the architecture of the LASE algorithm. LASE comprises two main modules: Social Relationship Inference (SRI) and Gifting. The SRI module uses counterfactual reasoning and a perspective-taking module to infer the social relationships between agents. These relationships are then used by the Gifting module to determine how much reward to share with other agents. The figure shows the flow of information between the environment, the agent, and the two modules.

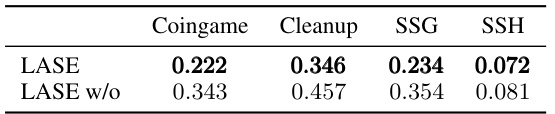
This table presents the average gifting weights assigned by LASE and its variant (LASE w/o) to other agents during the final 10,000 episodes of their self-play training across four different social dilemma environments: Coingame, Cleanup, SSG, and SSH. It shows how the gifting strategy changes when the perspective-taking module is removed (LASE w/o), providing insight into its impact on the distribution of rewards.

In-depth insights
#

Empathy in MARL
#

The concept of ‘Empathy in MARL’ introduces a fascinating avenue for enhancing multi-agent reinforcement learning. Traditional MARL often struggles to balance cooperation and competition effectively, particularly in mixed-motive games. Empathy, by enabling agents to understand and respond to the emotional states and intentions of others, offers a potential solution. Incorporating empathy could lead to more robust and cooperative agents that are less susceptible to exploitation. This involves developing computational models of empathy, which may involve techniques like counterfactual reasoning or perspective-taking. The success of this approach hinges on the ability to accurately infer co-players’ internal states, a task made challenging by the inherent complexity of multi-agent interactions and the partially observable nature of many environments. However, achieving truly empathetic AI remains a significant challenge, raising ethical and philosophical questions about the nature of artificial consciousness and the potential for unintended consequences. Further research should explore different computational models of empathy, evaluate their effectiveness in diverse MARL settings, and address the ethical implications of creating more empathetic AI agents.

LASE Algorithm
#

The LASE algorithm, designed for mixed-motive multi-agent reinforcement learning, cleverly addresses the challenge of balancing altruism and self-interest. Its core innovation lies in its empathy-based gifting mechanism, where agents dynamically allocate rewards to collaborators based on inferred social relationships. This approach deviates from traditional methods, moving away from centralized training and information sharing. Instead, LASE uses a distributed model and employs counterfactual reasoning to estimate each co-player’s contribution, informing its gifting decisions. The algorithm incorporates a perspective-taking module which further enhances its effectiveness in partially observable environments by predicting co-players’ policies. This sophisticated model allows LASE to dynamically adapt its strategy, promoting group collaboration without compromising individual gains and demonstrating resilience against exploitation. Overall, the LASE algorithm showcases the potential of integrating cognitive empathy into MARL, leading to more nuanced and effective solutions in complex social dilemmas.

Gift-Based Cooperation
#

Gift-based cooperation, as explored in the context of multi-agent reinforcement learning (MARL), presents a compelling approach to fostering collaboration in mixed-motive games. The core idea is that agents can strategically transfer a portion of their rewards to others as ‘gifts,’ thereby influencing the reward structures of their co-players and encouraging more cooperative behavior. This mechanism effectively addresses the challenge of balancing altruism and self-interest, as agents can adapt their gifting strategies based on the perceived trustworthiness and contributions of other agents. The success of this approach hinges on several factors, including the design of the gifting mechanism itself (e.g., zero-sum gifting, adaptive gifting based on social relationships), the learning algorithms used by the agents, and the specific characteristics of the game environment. A significant advantage of gift-based cooperation is its decentralized nature, eliminating the need for a central controller to manage reward allocation, thereby making it more suitable for real-world scenarios. However, this approach also raises several challenges. Determining optimal gifting strategies can be computationally expensive. Counterfactual reasoning and perspective-taking are vital for effective gift allocation, and accurate inference of co-players’ intentions and actions is crucial for avoiding exploitation. The choice of the appropriate social relationship metric for guiding gift allocation is also significant, as it directly impacts the fairness and efficiency of cooperation. Future research should focus on developing more sophisticated gifting mechanisms that are robust to uncertainty, scalable to large numbers of agents, and capable of adapting to dynamically changing social relationships in complex environments. Furthermore, ethical considerations regarding fairness and the potential for manipulation should be carefully addressed.

Social Relationship Inference
#

The proposed method for “Social Relationship Inference” is a crucial component of the LASE algorithm, aiming to foster altruistic cooperation while mitigating exploitation. It leverages counterfactual reasoning to estimate the impact of each co-player’s actions on the focal agent’s reward. This is achieved by comparing the estimated Q-value of the current joint action with a counterfactual baseline that marginalizes a single co-player’s action, thereby isolating their specific contribution. The method addresses the challenge of partial observability by incorporating a perspective-taking module. This module simulates each co-player’s local observation, facilitating the prediction of their policy distribution. In essence, the inference mechanism provides a nuanced measure of “friendliness”, guiding the gifting strategy by providing a continuous metric for social relationships. This innovative approach goes beyond simple reward sharing, moving towards a more sophisticated understanding of dynamic social interactions in multi-agent environments.

Fairness & Scalability
#

The concept of fairness in multi-agent systems is multifaceted. A fair system should ensure that all agents receive equitable rewards and opportunities, irrespective of their initial conditions or actions. LASE’s approach to reward sharing based on empathetically inferred social relationships aims to address this. While achieving perfect fairness across diverse agent strategies in complex environments is challenging, LASE’s mechanism of zero-sum gifting strikes a balance between altruism and self-preservation, mitigating exploitation. Scalability is crucial for real-world applications, and LASE’s decentralized nature enables it to handle a growing number of agents. Further research should focus on quantifying fairness more rigorously, such as through established metrics, and on analyzing LASE’s performance across a broader range of agent types and environmental complexities. Addressing potential issues like free-riding behavior and adaptive strategies of adversarial agents is important in assessing the overall long-term fairness and robustness of the system.

More visual insights
#

More on figures

This figure shows the results of a theoretical analysis of LASE’s learning process in iterated matrix games. The surface plot displays the probability of LASE agents cooperating (vertical axis) as a function of two game parameters: T (temptation to defect) on the horizontal axis and S (sucker’s payoff) on the depth axis. The plot shows that LASE converges to higher cooperation probability as the temptation to defect (T) decreases and the sucker’s payoff (S) increases. The dashed lines and shaded regions divide the parameter space into four well-known game types (Prisoner’s Dilemma (PD), Stag Hunt (SH), Snowdrift (SG), and Harmony). The red dot represents the specific game parameters used in the IPD experiments presented in the paper.

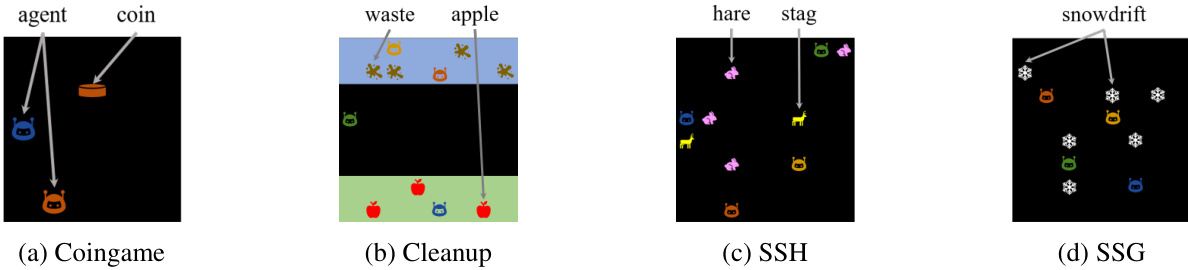
This figure shows four different spatially extended social dilemmas (SSDs): Coingame, Cleanup, Sequential Stag-Hunt (SSH), and Sequential Snowdrift Game (SSG). Each subfigure displays a simplified visual representation of the game’s environment, illustrating the agents’ positions, resources, and potential interactions. The map sizes are indicated in the caption, showing the scale of each game. These diverse SSDs serve to evaluate the proposed LASE algorithm in more complex and dynamic environments than simple matrix games.

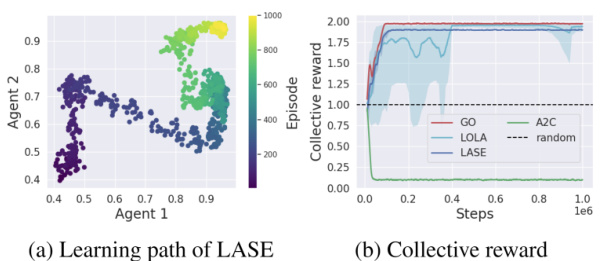
This figure shows the results of the Iterated Prisoner’s Dilemma (IPD) experiment. Panel (a) is a scatter plot visualizing the learning paths of two LASE agents, showing their cooperation probabilities over time. The agents begin with low cooperation probabilities but gradually converge towards high cooperation (around 0.93). Panel (b) compares the collective reward obtained by LASE with other baselines (GO, LOLA, A2C, and random) over training steps. The plot displays the mean collective reward and standard deviation across five random seeds. LASE demonstrates superior performance in achieving a higher collective reward and consistent cooperation compared to the other baselines.

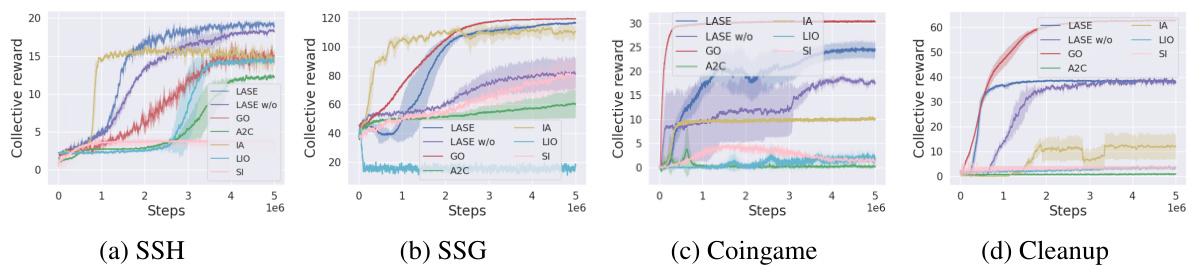
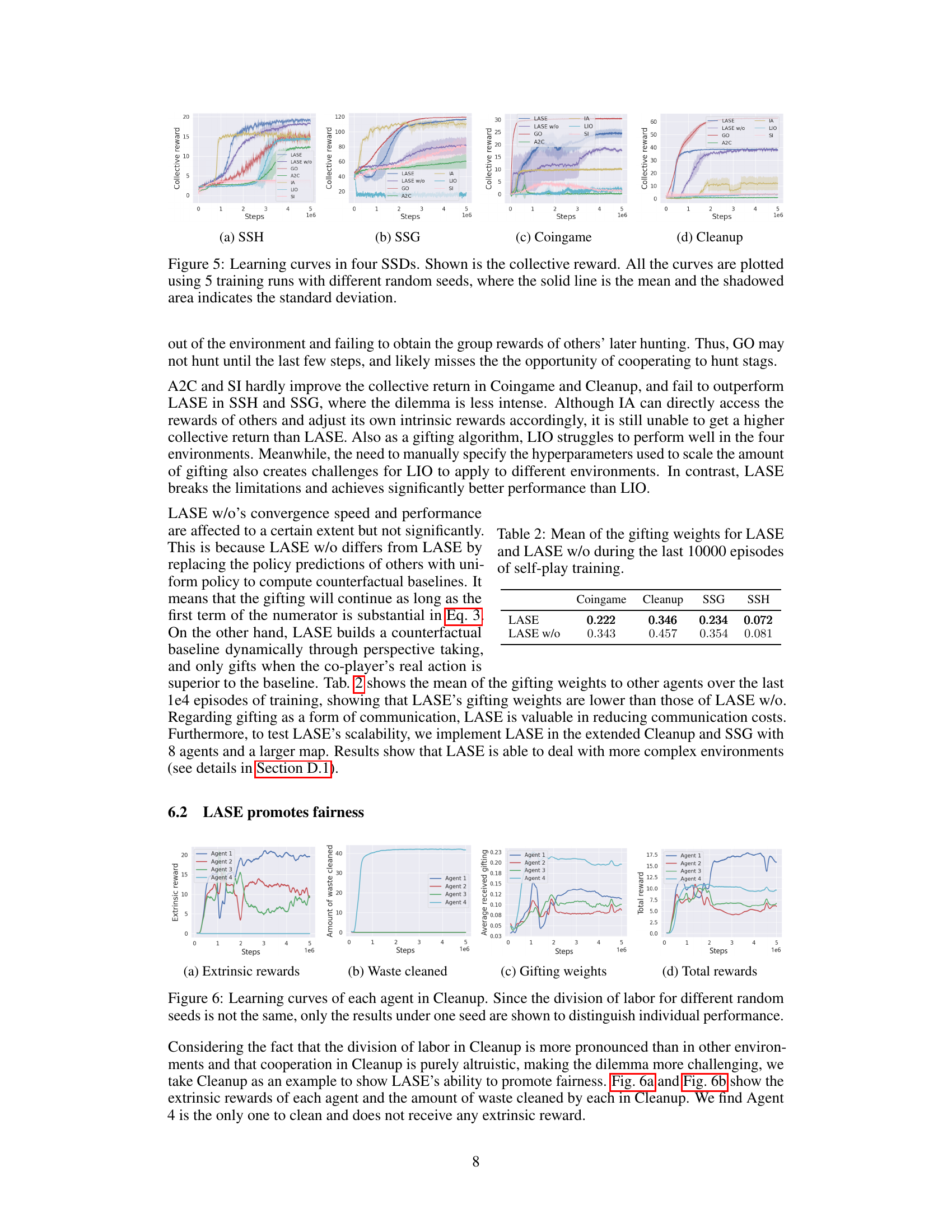
This figure presents the learning curves for four different spatially extended social dilemmas (SSDs) using LASE and other baseline algorithms. The x-axis represents the number of steps in training, and the y-axis displays the collective reward achieved by the agents. Each line shows the average performance over five runs with different random seeds, with a shaded region indicating the standard deviation. The figure demonstrates how LASE compares to other methods like A2C, LIO, IA, SI, and GO in different scenarios. It provides a visual representation of the comparative effectiveness of LASE for promoting cooperation across different types of mixed-motive environments.

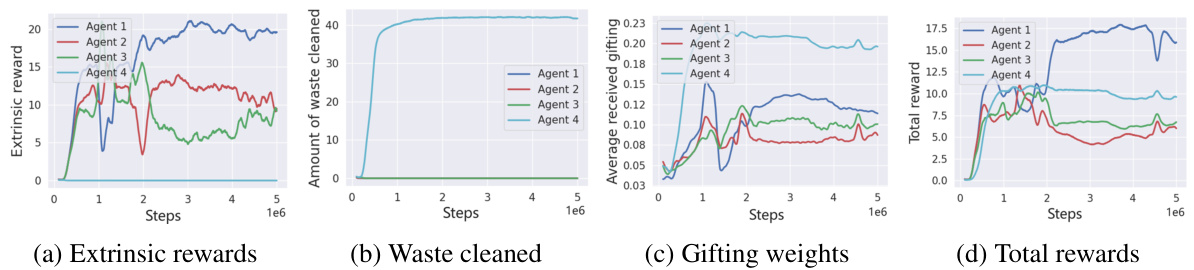
This figure shows the learning curves for four agents in the Cleanup environment. It displays the extrinsic rewards earned by each agent, the amount of waste cleaned by each agent, the average gifting weights each agent received from the other agents, and the total rewards for each agent over time. The figure highlights the impact of LASE’s gifting mechanism in promoting fairness and mitigating exploitation. Note that since the division of labor varies with different random seeds, only results from one specific seed are displayed for easier analysis.

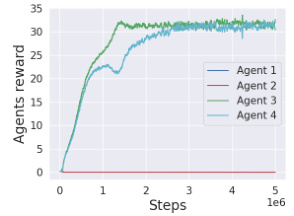
This figure shows the learning curves for four agents in the Cleanup environment. The top graph displays the extrinsic rewards earned by each agent over training steps, showing a significant disparity in the rewards earned. The second graph illustrates the amount of waste each agent cleans up. Agent 4 is the only one that cleans waste, and, thus receives no direct rewards from cleaning. The third graph shows the gifting weights from other agents to each agent. Agent 4 receives substantially more gifting weight compared to the other agents, suggesting a recognition of its contribution. The final graph shows the total rewards (extrinsic + gifting) received by each agent, illustrating that while Agent 4 receives no direct rewards from cleaning, it receives a high total reward through the gifting mechanism, balancing the inequality of the extrinsic rewards.

This figure shows how LASE’s gifting weights change over time when interacting with three different types of agents: a cooperator (always performs the helpful action), a defector (always performs the selfish action), and a random agent. The shaded areas represent the standard deviation across multiple runs. The results demonstrate LASE’s ability to dynamically adapt its gifting strategy based on the observed behavior of its co-players, rewarding cooperators more and defectors less.

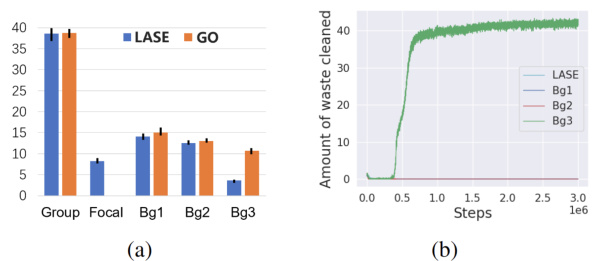
This figure shows the results of an experiment where one LASE agent (or GO agent for comparison) interacts with three A2C agents in the Cleanup environment. Part (a) presents a bar chart comparing the average reward obtained by the LASE group and the GO group after 30,000 training episodes. The LASE group’s reward is shown after the gifting mechanism is applied. The chart breaks down the rewards for the whole group and each individual agent (LASE, three A2C agents). Part (b) is a line graph illustrating the amount of waste cleaned by each agent (LASE and three A2C agents) over 3,000,000 steps.

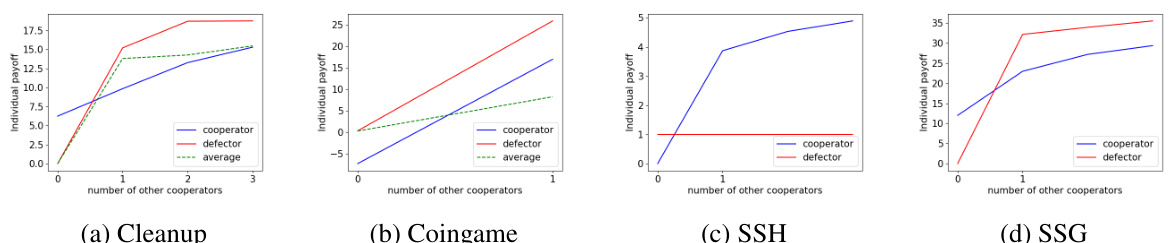
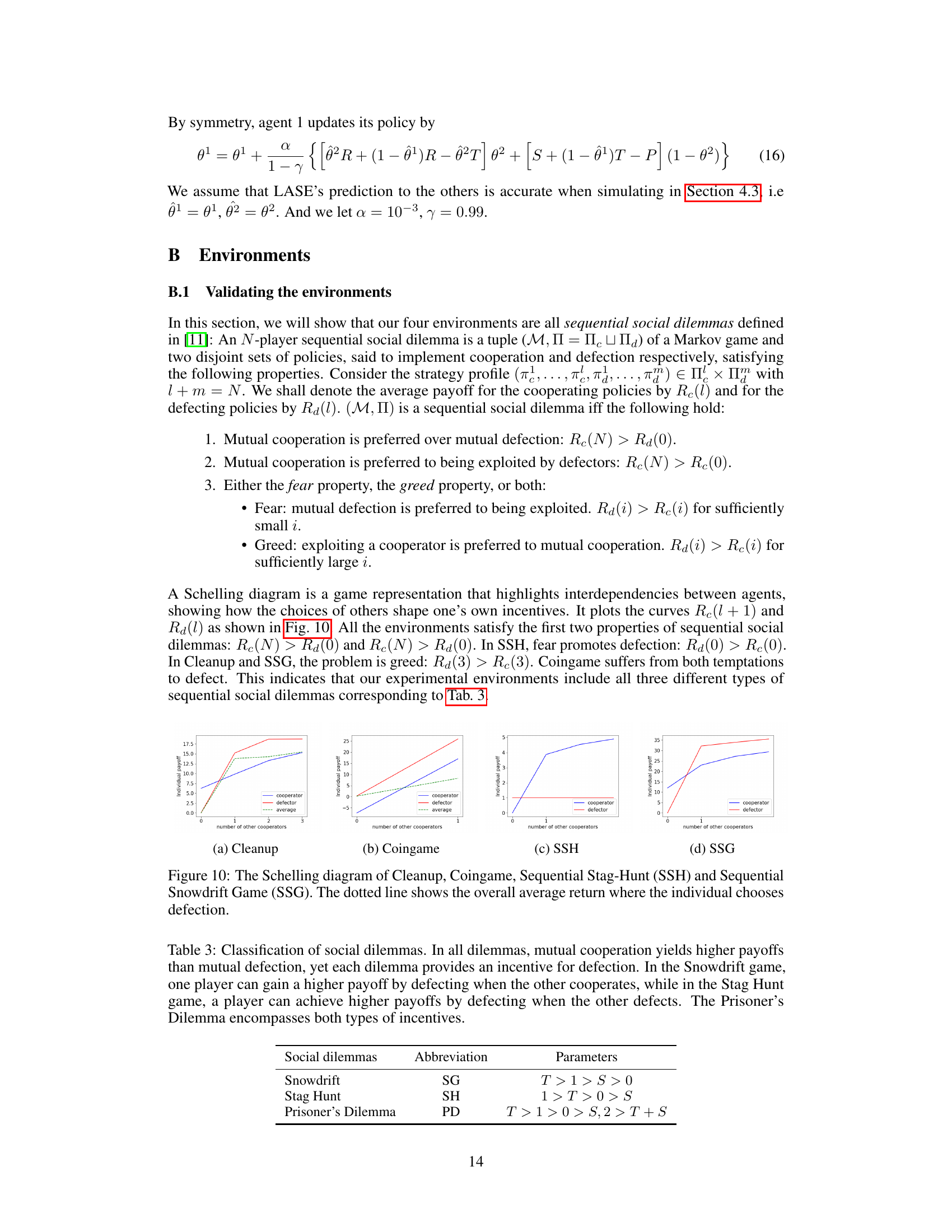
This figure presents Schelling diagrams for four sequential social dilemmas: Cleanup, Coingame, Sequential Stag-Hunt (SSH), and Sequential Snowdrift Game (SSG). A Schelling diagram illustrates the interdependencies between agents, showing how the choices of others influence an agent’s incentives. The x-axis represents the number of other cooperators, and the y-axis shows the average payoff for either choosing cooperation or defection. The dotted line indicates the overall average return when an agent chooses to defect. These diagrams visually demonstrate the nature of the social dilemma in each game, highlighting the conditions under which cooperation or defection is preferred.