↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Image restoration using deep learning often suffers from deviations between single model predictions and ground truths. Ensemble learning can mitigate these issues by combining predictions from multiple models, but most existing methods focus on ensemble learning during model training, limiting their flexibility and efficiency. Existing post-training ensemble methods often rely on simple averaging or regression, which are less effective and efficient.
This paper proposes EnsIR, a novel post-training ensemble algorithm. EnsIR formulates the ensemble problem using Gaussian mixture models (GMMs) and employs an expectation-maximization (EM)-based algorithm to estimate ensemble weights, which are stored in a lookup table for efficient inference. This approach is both model-agnostic and training-free, enabling seamless integration with various pre-trained models. Experiments show that EnsIR consistently outperforms regression-based methods and averaging approaches on multiple image restoration tasks.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel, model-agnostic, and training-free ensemble algorithm (EnsIR) for image restoration. EnsIR addresses the limitations of existing methods by efficiently combining predictions from multiple pre-trained models without requiring retraining. This significantly enhances the flexibility and performance of image restoration systems, particularly relevant in industrial settings where model flexibility is crucial. The algorithm’s generalizability and efficiency make it a valuable tool for researchers and practitioners alike, opening up new avenues for improving image restoration across various applications.
Visual Insights#

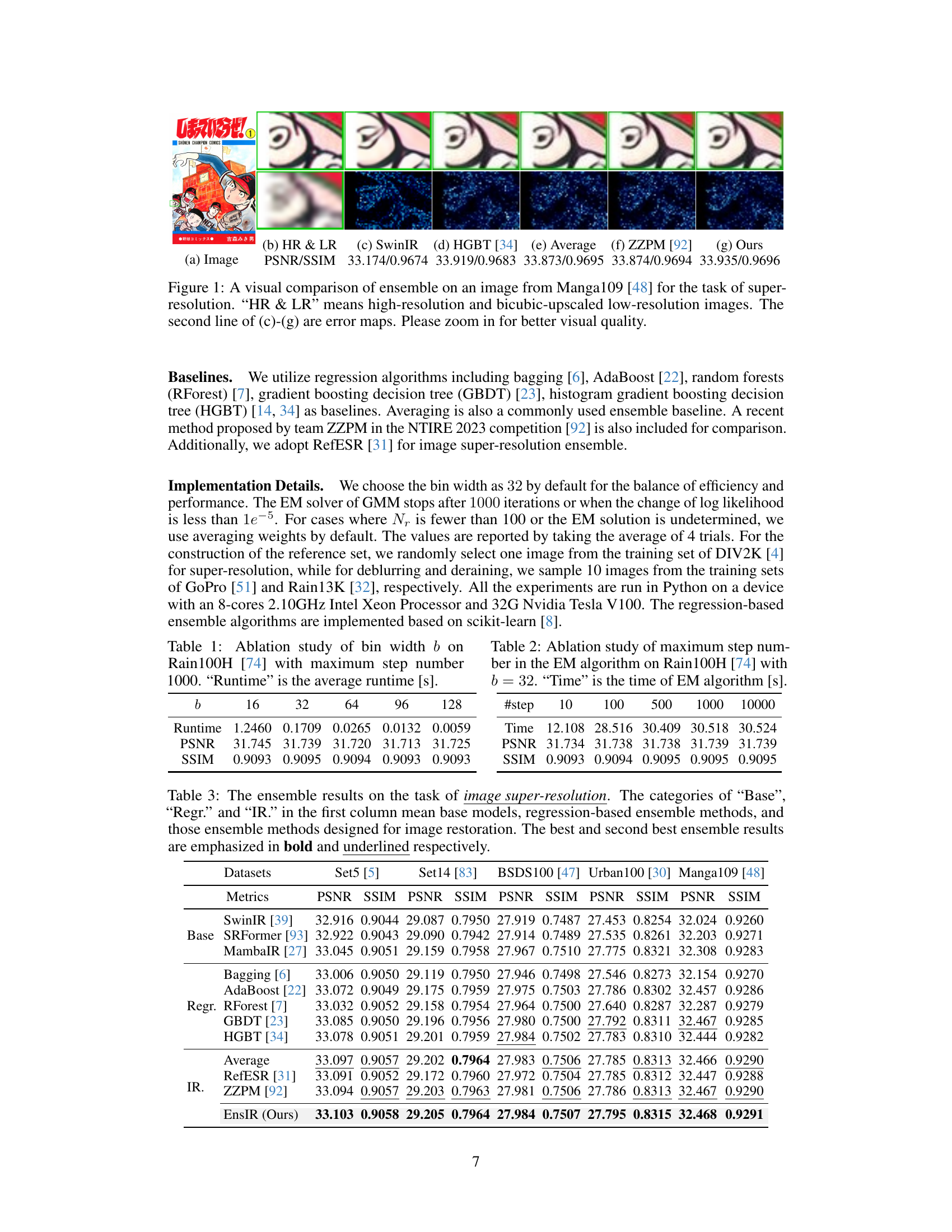
This figure compares different super-resolution methods on a sample image from the Manga109 dataset. It shows the original high-resolution (HR) image, a low-resolution (LR) bicubic upscaled version, and the results from SwinIR, HGBT (Histogram Gradient Boosting), average ensemble, ZZPM (a state-of-the-art method from the NTIRE 2023 competition), and the proposed EnsIR method. The bottom row displays error maps for visual comparison of the quality of results. EnsIR produces the visually best results according to this example.

This table presents a comparison of different ensemble methods on the task of image super-resolution. It compares the performance (PSNR and SSIM) of various base models (CNNs, ViTs, etc.) against several ensemble techniques, including regression-based methods and those specifically designed for image restoration. The results highlight the superior performance of the proposed EnsIR method.
In-depth insights#
EnsEMBLE Inference#
Ensemble inference methods combine predictions from multiple models to improve accuracy and robustness. The core idea is to leverage the strengths of diverse models, each potentially excelling in different aspects of the task. This approach offers several advantages, including improved generalization (reducing overfitting), increased stability (less susceptible to noise), and better handling of complex patterns. However, ensemble inference strategies need careful design. Simple averaging, although computationally inexpensive, may not be optimal. More sophisticated techniques like weighted averaging, where weights reflect model performance or confidence, or using more complex combination strategies, are often beneficial but introduce increased computational costs. The choice of ensemble method should consider the specific task, model characteristics, and computational constraints. Efficient ensemble methods are crucial for deployment in real-time applications where computational resources are limited. Furthermore, understanding how model diversity contributes to improved performance is important for selecting and training suitable base models for ensemble inference.
GMM Weight Estimation#
GMM weight estimation, in the context of ensemble image restoration, is a crucial step for effectively combining predictions from multiple models. The core idea is to represent the ensemble problem as a Gaussian Mixture Model (GMM), where each model’s prediction corresponds to a Gaussian component. The GMM weights, representing the contribution of each model, are then estimated using the Expectation-Maximization (EM) algorithm. This approach leverages the statistical properties of Gaussian distributions to find optimal weights, which can be efficiently stored in a lookup table for fast inference. A key advantage is the model-agnostic nature of GMM weight estimation; it’s applicable to diverse pre-trained models without requiring retraining. The algorithm partitions pixel values into range-wise bins, simplifying the weight estimation process to multiple univariate GMMs, which are more computationally tractable than their multivariate counterparts. The use of a lookup table (LUT) significantly speeds up inference, making the ensemble approach practically efficient. Finally, the selection of appropriate bin widths and EM algorithm parameters are critical to achieving a balance between computational efficiency and the accuracy of the estimated weights. Careful consideration of these factors is essential to the overall success of the GMM-based ensemble method.
LUT-Based Inference#
LUT-based inference offers a compelling approach to accelerating the inference stage of ensemble methods in image restoration. By pre-computing and storing ensemble weights in a lookup table (LUT), the computationally expensive process of determining these weights during inference is eliminated. This is particularly beneficial for computationally intensive tasks like image restoration where real-time performance is often crucial. The model-agnostic nature of LUT-based inference is a significant advantage, enabling seamless integration with a wide variety of pre-trained image restoration models. However, the LUT approach introduces a trade-off between accuracy and efficiency. The size of the LUT scales with the number of bins and models, potentially leading to increased memory requirements and decreased accuracy if the bin size is too large. Therefore, careful consideration needs to be given when selecting appropriate bin sizes and balancing speed versus accuracy. Furthermore, the success of this method heavily relies on the representativeness of the reference set used for LUT generation. A poorly chosen reference set may lead to inaccurate ensemble weights, and hence reduced restoration performance, highlighting the need for a thoroughly curated reference set that encapsulates the variations in real-world image data.
Model-Agnostic Method#
A model-agnostic method in a research paper signifies an approach independent of any specific machine learning model. This is a significant advantage as it offers flexibility and broad applicability. Unlike model-specific methods, which are tailored to a particular architecture or algorithm (e.g., convolutional neural networks, transformers), model-agnostic techniques can be applied to a wider range of pre-trained models without requiring retraining or modification. This versatility is crucial as it facilitates efficient integration with existing tools, reduces development time, and allows for experimentation across diverse model types to potentially discover optimal model combinations. The core focus of a model-agnostic method lies in the processing or combination of the outputs from different models, rather than influencing their inner workings. This usually involves post-processing steps which could include ensemble methods like weighted averaging, or more sophisticated techniques such as Gaussian Mixture Models (GMMs) or other statistical approaches to combine the predictions. The evaluation of a model-agnostic method thus centers on its effectiveness in improving overall performance or robustness across a variety of base models, regardless of their underlying structure.
Future Enhancements#
Future enhancements for this ensemble image restoration method could focus on several key areas. Improving efficiency is crucial, potentially through optimized binning strategies, more efficient GMM parameter estimation techniques, or leveraging parallel processing capabilities. Exploring alternative ensemble methods beyond GMMs, such as robust regression techniques or novel deep learning architectures for weight aggregation, might yield further improvements in accuracy and robustness. Extending the model’s applicability to a broader range of image restoration tasks and degradation types would enhance its versatility. Addressing limitations related to handling cases where all base models perform poorly or scenarios with highly variable image content warrants attention. Finally, developing methods to automatically determine optimal bin sizes or parameters for different image types and degradation conditions could reduce manual intervention and improve automation.
More visual insights#
More on figures

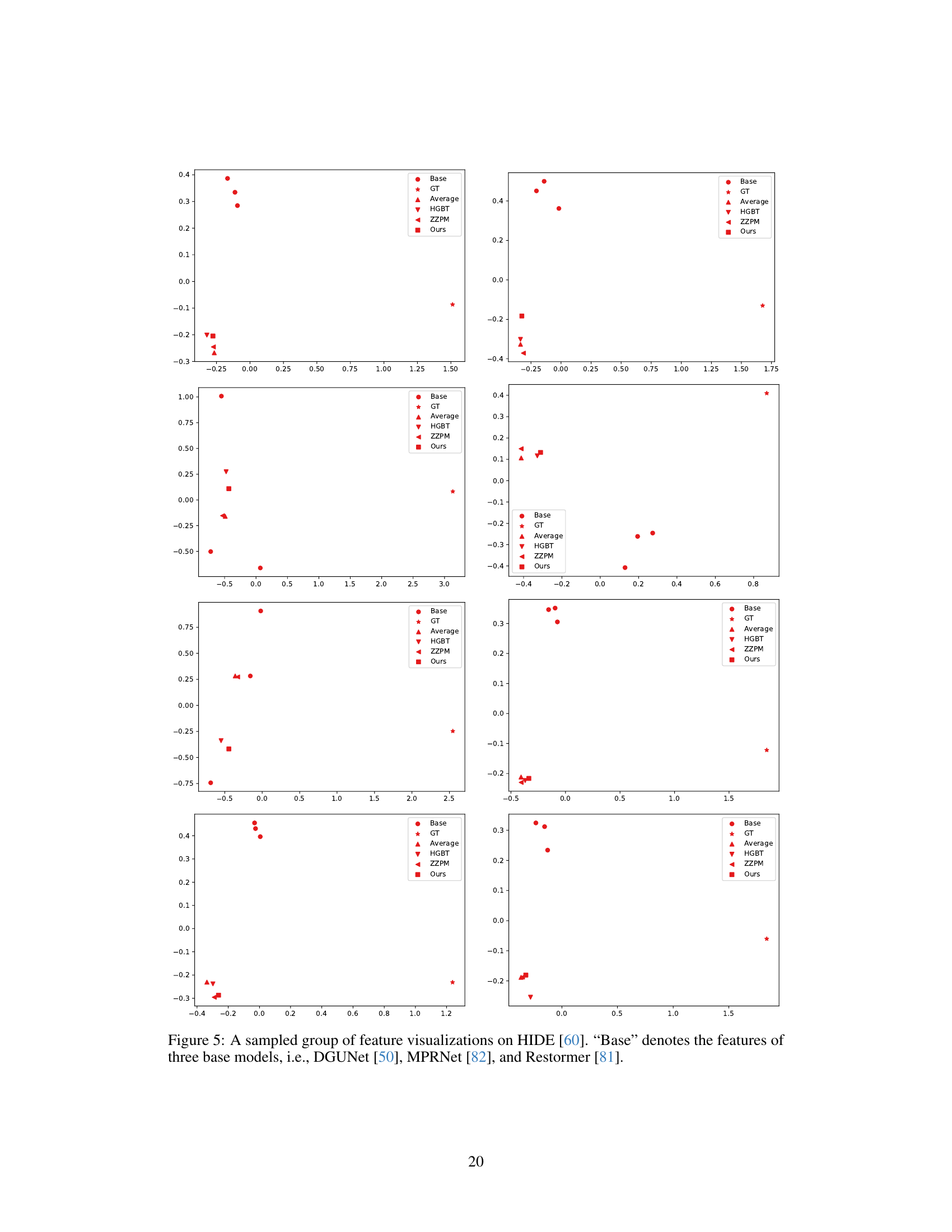
This figure shows a comparison of ensemble weight visualizations using different methods on an image from the HIDE dataset. The figure includes ground truth, results from three base models (DGUNet, MPRNet, Restormer), and the results of averaging, ZZPM, and the proposed EnsIR method. Each visualization section shows the weights assigned to each base model’s prediction for each region of the image, offering a visual representation of how the different methods weight the contributions of the base models.

This figure shows the distribution of pixel values within specific ranges (bins) for different image restoration models on the HIDE dataset. It demonstrates the distribution of ground truth and model predictions for each bin, illustrating the underlying assumption of Gaussian distribution for range-wise ensemble weights in the proposed EnsIR algorithm.

This figure displays a comparison of ensemble weight maps for different methods on a sample image from the HIDE dataset for image deblurring. It demonstrates the weight distributions assigned by various methods including averaging, ZZPM, and the proposed EnsIR algorithm. The base models used are DGUNet, MPRNet, and Restormer. The figure shows how EnsIR assigns more detailed weights, preserving textures better than the other methods.

This figure shows a comparison of ensemble weight maps for different methods on a sample image from the HIDE dataset. Four base models (DGUNet, MPRNet, Restormer) are used, along with averaging, ZZPM, and the proposed EnsIR method. The figure demonstrates how the proposed EnsIR learns more detailed and nuanced weights compared to simpler averaging or regression-based approaches. Each column represents a different method, showing the base model predictions, ground truth, and the resulting ensemble weight maps.
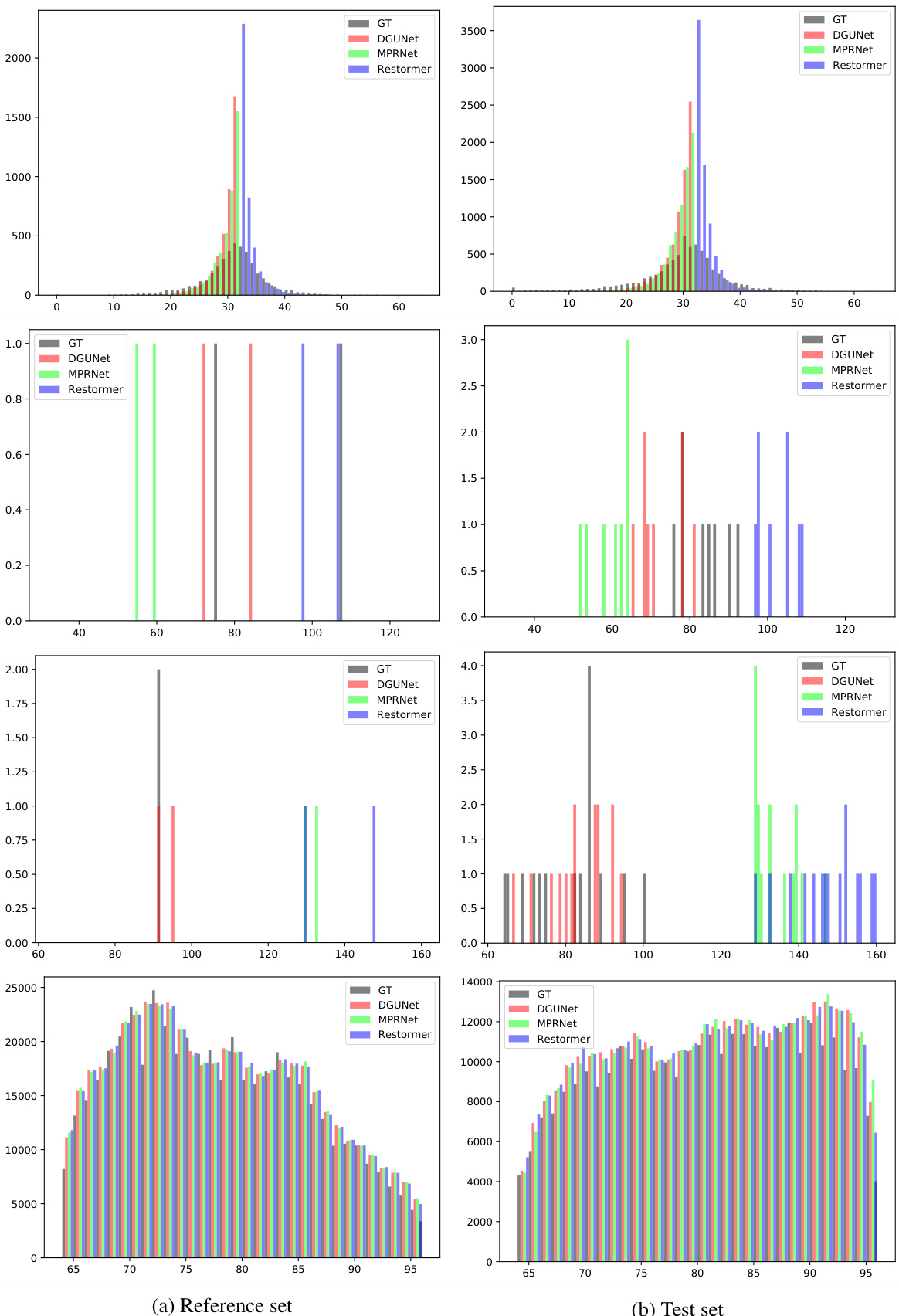
This figure shows the distribution of pixel values within different bin sets for both the reference and test sets. It visually demonstrates the Gaussian-like distribution assumption used in the proposed ensemble method (EnsIR). The different rows represent different combinations of bin ranges selected for analysis. Each bar shows the frequency of pixels within a specific range for different base models and the ground truth. This visualization helps in understanding how the model determines the weights for the ensemble.

This figure compares different super-resolution methods on a sample image from the Set14 benchmark dataset. The first image shows the original high-resolution image. The next images show the low-resolution image upscaled using bicubic interpolation, and then results from several different super-resolution models (SwinIR, SRFormer, HGBT, averaging, ZZPM, and the proposed EnsIR method). The caption notes that zooming in will improve the visual comparison, implying subtle differences are present between the methods.

This figure compares different super-resolution methods on a single image from the Urban100 dataset. It shows the original high-resolution (HR) image, the bicubic upscaled low-resolution image, results from SwinIR, SRFormer, HGBT, average ensemble, ZZPM’s method and the proposed EnsIR method. The PSNR/SSIM scores are provided for each method, allowing for a quantitative comparison of their performance. The visual differences between the methods, particularly in finer details, are highlighted to showcase the qualitative improvement achieved by the proposed method.

This figure compares the results of different super-resolution methods on a sample image from the Urban100 dataset. It shows the original high-resolution (HR) image, the bicubic upsampled low-resolution image, results from SwinIR, MambaIR, HGBT, averaging, ZZPM, and the proposed EnsIR method. The PSNR and SSIM values are provided for quantitative comparison, highlighting the improved performance of EnsIR.
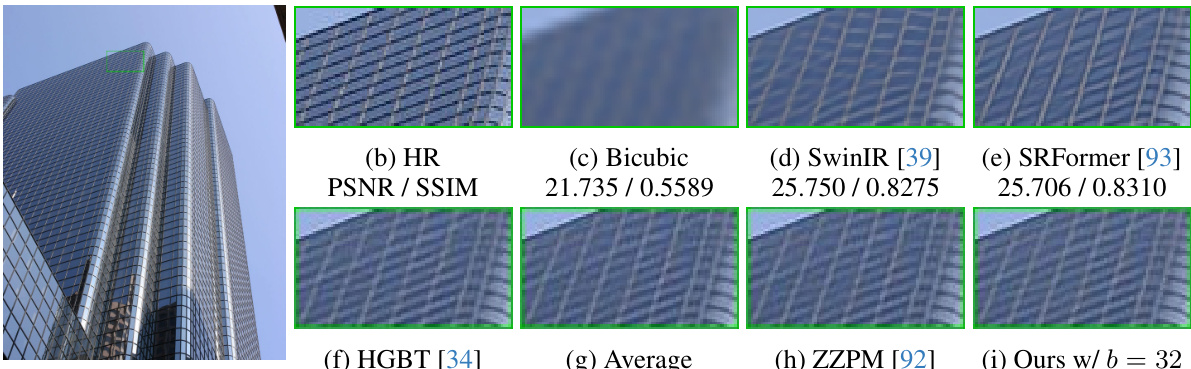
This figure compares different super-resolution methods on a specific image from the Urban100 dataset. It shows the original high-resolution image, a bicubic upscaled low-resolution image, results from SwinIR, SRFormer, HGBT, a simple averaging ensemble, the ZZPM method, and the proposed EnsIR method. The PSNR and SSIM values are provided for quantitative comparison, highlighting the superior performance of the EnsIR method.

This figure shows a visual comparison of different ensemble methods on a blurry image from the HIDE dataset for image deblurring. The methods compared include: a blurry image, MPRNet, HGBT, average ensemble, ZZPM, and the proposed EnsIR method with bin widths of 64 and 32. The results are presented in terms of PSNR and SSIM values, along with visual comparisons of the deblurred images. The figure aims to highlight the improved performance of the proposed EnsIR method, especially in preserving fine details and textures compared to other techniques.

This figure compares different ensemble methods on a blurry image from the RealBlur-J dataset. The methods compared include the baseline HGBT, averaging, ZZPM, and the proposed EnsIR method. The figure shows the original blurry image, the ground truth, results of the individual base models used in the ensemble (MPRNet and Restormer), the results of each ensemble method, and the corresponding PSNR/SSIM values. The visual comparison highlights that the proposed EnsIR method outperforms other methods in terms of both quantitative metrics and visual quality.

This figure shows a visual comparison of different ensemble methods on a blurry image from the RealBlur-J dataset. The image is deblurred using several base models (MPRNet, Restormer, HGBT), as well as averaging, ZZPM, and the proposed EnsIR method. The results demonstrate the effectiveness of EnsIR in producing sharper and higher-quality deblurred images compared to other methods.

This figure shows a visual comparison of different ensemble methods on a rainy image from the Rain100H dataset. The image is first shown in its original, rainy state. It then shows the ground truth (Clean), results from applying individual deraining models (MPRNet, MAXIM), results from the HGBT method, the average ensemble, ZZPM’s ensemble, and finally the results from EnsIR (the proposed method) with a bin width of 32. The PSNR/SSIM values for each method are given below the images. The figure highlights the improvement in deraining quality achieved by the proposed EnsIR method compared to other ensemble techniques.

This figure shows a visual comparison of different ensemble methods on a single image from the Rain100L dataset for image deraining. The top row displays the original clean image, the rainy image, and the results from three individual deraining models (MPRNet, Restormer, and HGBT). The bottom row shows the results of the averaging ensemble method, the ZZPM method, and the proposed EnsIR method. The PSNR and SSIM values are provided for quantitative comparison. The green boxes highlight regions where visual differences are more apparent. Overall, the figure demonstrates the visual improvements achieved by the proposed ensemble method.

This figure compares different ensemble methods on a single image from the Rain100L dataset for image deraining. The image shows a woman under an umbrella, and the results highlight differences in how each method handles rain streaks and overall image quality. The methods include a baseline of using only the MPRNet and Restormer models, the HGBT algorithm, simple averaging, the ZZPM method, and the authors’ proposed EnsIR method. The results show that EnsIR produces a visually superior result with enhanced details and reduced artifacts compared to other approaches.

This figure shows a visual comparison of different image deraining methods on a specific image from the Test1200 dataset. The methods compared include the base models MAXIM and Restormer, the ensemble methods HGBT, averaging, ZZPM, and the proposed EnsIR method. The results are presented in terms of PSNR and SSIM values, and visually, showing the derained image produced by each method. The goal is to showcase the performance improvement achieved by EnsIR compared to other baselines and other ensemble methods.

This figure compares the visual results of different ensemble methods on a single image from the Test2800 dataset for image deraining. It shows the original clean image, the rainy image, and the results of MPRNet, MAXIM, HGBT, averaging, ZZPM, and the proposed EnsIR method. The caption highlights that zooming in will reveal more details of the visual differences in image quality.
More on tables
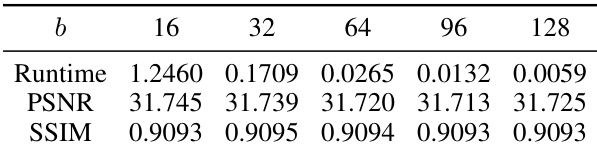
This table shows the ablation study of the bin width (b) parameter used in the EnsIR algorithm. The study was conducted on the Rain100H dataset with a maximum of 1000 steps in the Expectation-Maximization (EM) algorithm. The table presents the average runtime in seconds, the Peak Signal-to-Noise Ratio (PSNR), and the Structural Similarity Index Measure (SSIM) for different bin widths (16, 32, 64, 96, 128). It demonstrates the trade-off between computational efficiency (runtime) and performance (PSNR and SSIM) as the bin width varies.
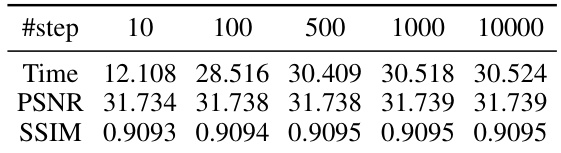
This table shows the ablation study of the maximum step number in the Expectation-Maximization algorithm used in the paper’s ensemble method. The experiment was performed on the Rain100H dataset with a bin width (b) of 32. The table shows how the PSNR and SSIM metrics, and the runtime of the EM algorithm, change as the maximum number of steps is increased.
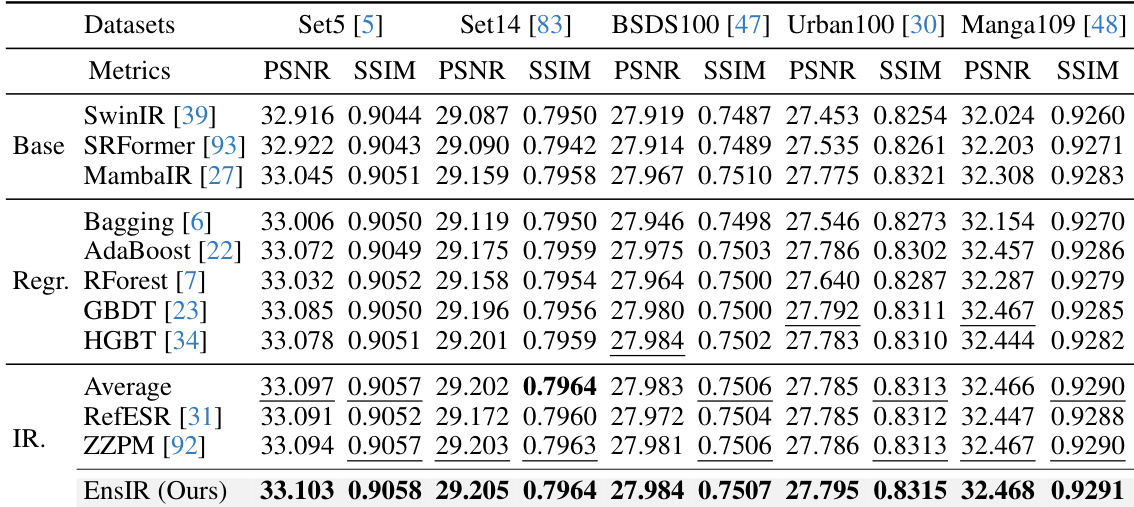
This table presents a comparison of different ensemble methods for image super-resolution. It shows the PSNR and SSIM scores achieved by various base models (CNNs, ViTs, etc.), regression-based ensemble methods, image restoration-specific ensemble methods, and the proposed EnsIR method. The results are presented for five benchmark datasets (Set5, Set14, BSDS100, Urban100, and Manga109). The best-performing methods for each dataset are highlighted.
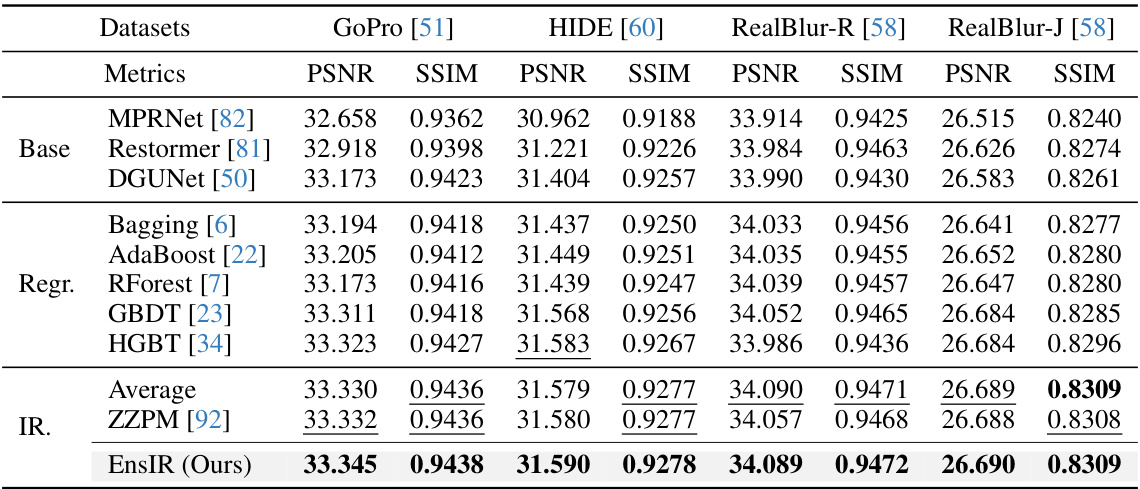
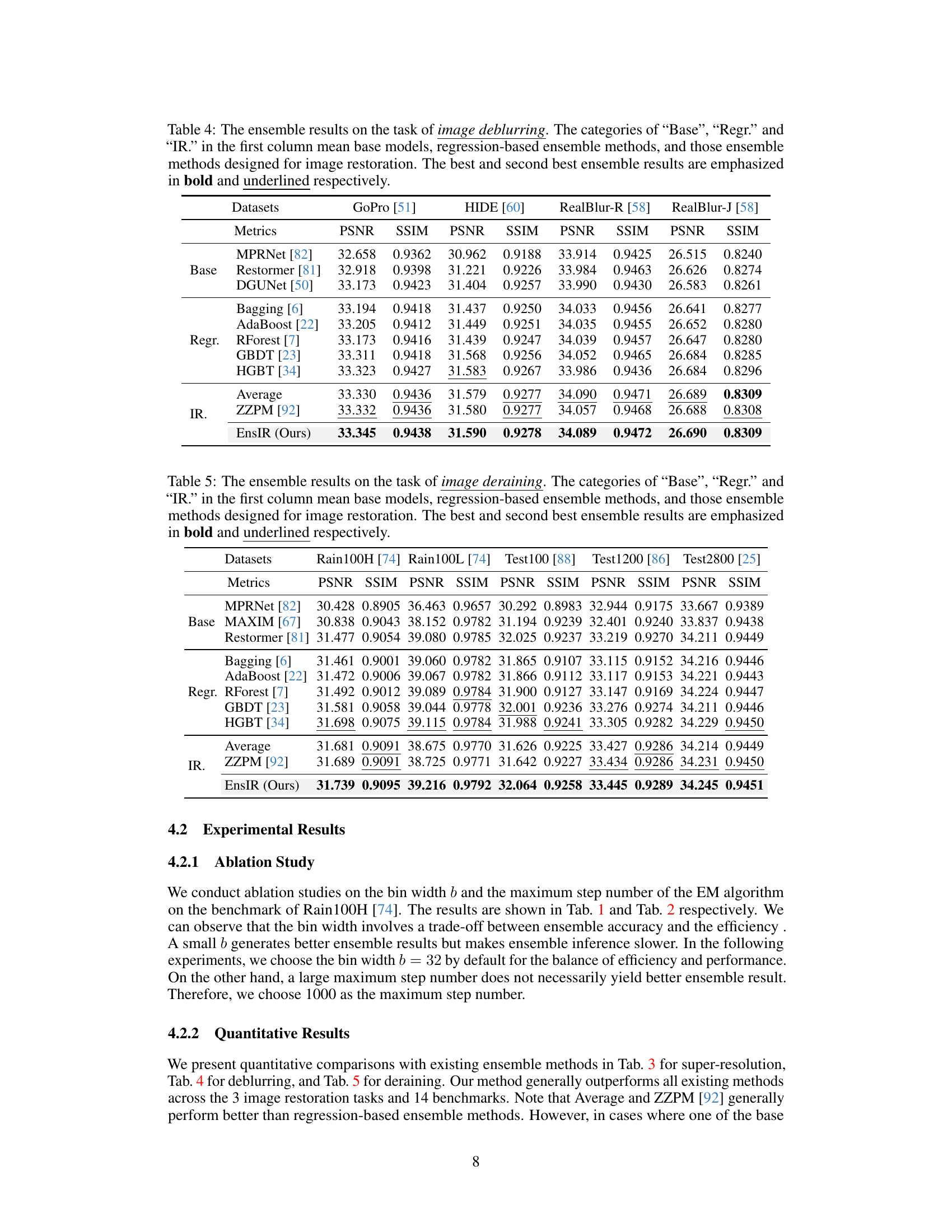
This table presents a quantitative comparison of different ensemble methods for image deblurring. It shows the PSNR and SSIM scores achieved by various base models (MPRNet, Restormer, DGUNet), regression-based ensemble methods (Bagging, AdaBoost, RForest, GBDT, HGBT), image restoration ensemble methods (Average, ZZPM), and the proposed EnsIR method. The results are evaluated on four datasets (GoPro, HIDE, RealBlur-R, RealBlur-J). The best performing methods are highlighted.

This table compares the performance of different ensemble methods on the image super-resolution task using various metrics (PSNR and SSIM) across five benchmark datasets (Set5, Set14, BSDS100, Urban100, and Manga109). It shows the results for individual base models (CNNs, ViTs, and Mambas), regression-based ensemble methods, image restoration-specific ensemble methods, averaging, and the proposed EnsIR method. The best and second-best results are highlighted.

This table presents the average runtime, in seconds, for each ensemble method tested on the Rain100H dataset for image deraining. The methods compared include Bagging, AdaBoost, Random Forest, GBDT, HGBT, Averaging, ZZPM, and the proposed EnsIR method. The runtime is a key factor in determining the efficiency and practicality of the method, especially in real-time applications.
Full paper#