↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current Bayesian deep learning often struggles with generating diverse neural networks for reliable uncertainty quantification. Standard methods, like using multiple random initializations, suffer from issues like permutation invariance and diminishing gradients when networks are too similar. This makes it difficult to obtain a good estimate of how confident the model is in its predictions. The naive similarity metrics lack permutation invariance and are inappropriate for comparing networks.
This paper introduces a novel approach using Centered Kernel Alignment (CKA) and Hyperspherical Energy (HE) to address these issues. The method projects the feature kernels onto a unit hypersphere, then minimizes the hyperspherical energy between kernels. This helps ensure that the network ensemble/posterior is diverse and well-distributed, leading to better uncertainty quantification. Experimental results show the method significantly outperforms existing baselines, particularly in uncertainty quantification and out-of-distribution detection tasks across various datasets and neural network architectures.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the critical need for improved uncertainty quantification in Bayesian deep learning. It introduces a novel approach to enhance diversity in ensemble and hypernetwork methods, leading to more robust and reliable uncertainty estimates. The findings have implications for various machine learning applications that require dependable uncertainty measures, such as outlier detection, safety-critical systems, and trustworthy AI. The proposed hyperspherical energy minimization of CKA offers a new tool for researchers and opens up avenues for further research in this crucial area.
Visual Insights#
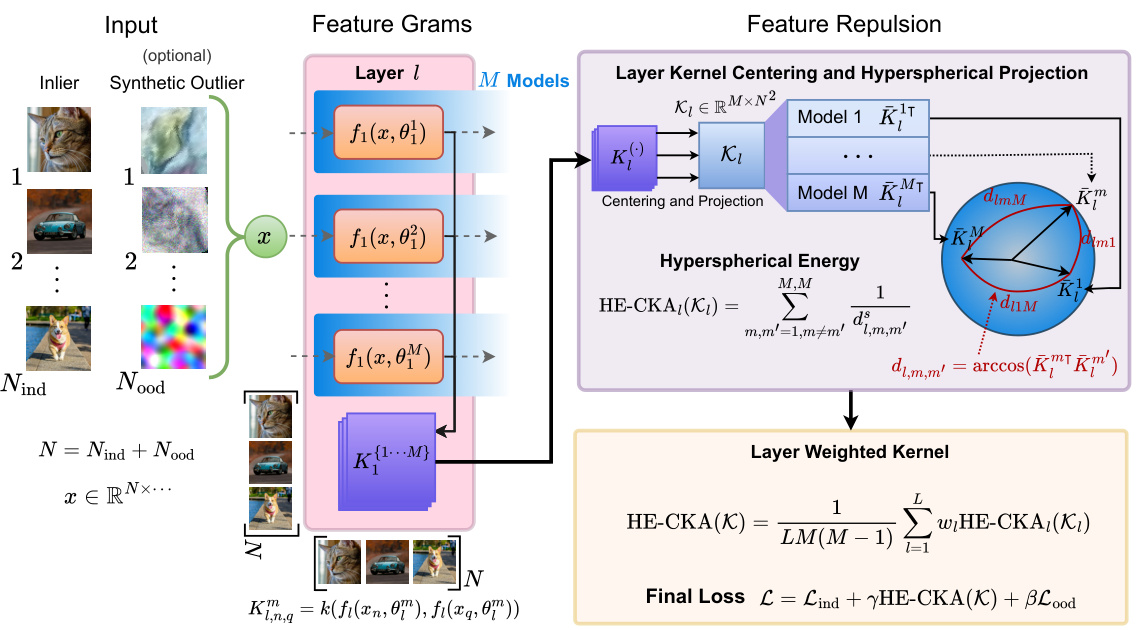
This figure illustrates the process of constructing a feature repulsive loss for enhancing diversity in Bayesian deep learning. It starts with a batch of input examples, optionally including synthetic outliers. Ensemble features from each layer are used to create centered Gram matrices. These matrices are then projected onto a unit hypersphere, and hyperspherical energy is calculated between the models. Finally, the layer-weighted hyperspherical energy is incorporated into the loss function to encourage diversity among models.
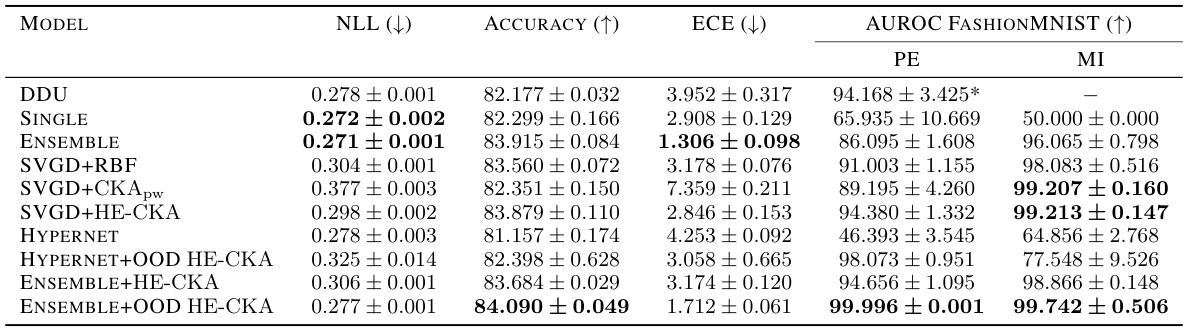
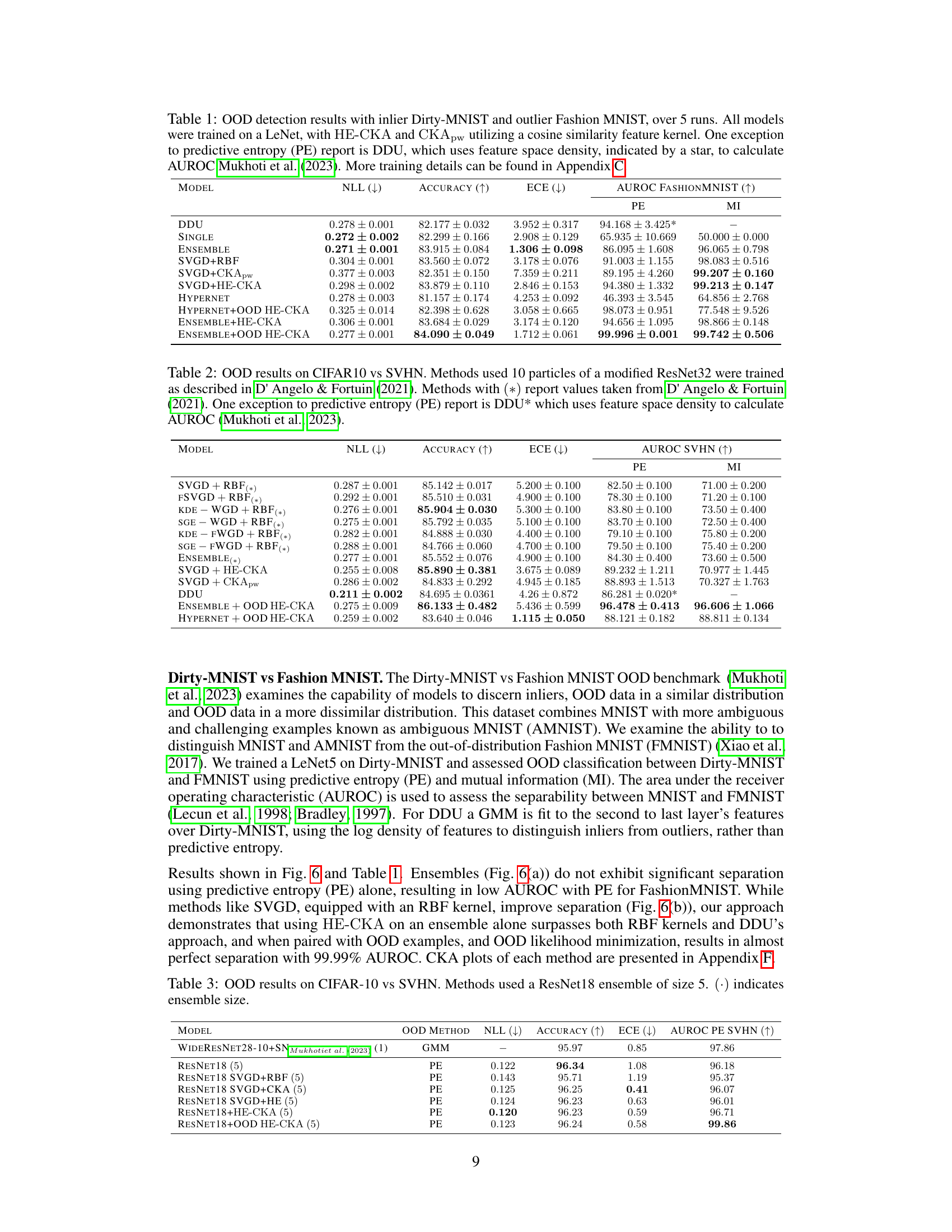
This table presents the results of out-of-distribution (OOD) detection experiments using different methods on the Dirty-MNIST and Fashion-MNIST datasets. It compares the performance of various methods, including those using the proposed HE-CKA and CKApw approaches, in terms of negative log-likelihood (NLL), accuracy, expected calibration error (ECE), and AUROC for FashionMNIST (as an OOD dataset). The table highlights the superior performance of methods incorporating HE-CKA, particularly when combined with out-of-distribution (OOD) data and an entropy term.
In-depth insights#
Bayesian Deep Ensembles#
Bayesian deep ensembles combine the strengths of Bayesian methods and ensemble learning to address challenges in deep learning. Bayesian methods offer principled ways to quantify uncertainty, crucial for reliable predictions, especially in scenarios with noisy or limited data. Ensemble methods, by combining predictions from multiple models, improve robustness and accuracy. Bayesian deep ensembles achieve this by training multiple deep neural networks with different initializations and/or variations in architecture. The resulting ensemble provides not just a single prediction, but also a distribution of predictions, enabling a more nuanced understanding of uncertainty. This approach is particularly effective in handling complex, high-dimensional data common in modern machine learning applications. A key challenge lies in efficiently managing and combining information from multiple models, often requiring sophisticated computational techniques. The effectiveness of Bayesian deep ensembles hinges on carefully selecting and training diverse models, ensuring their predictions capture different aspects of the data. Further research is focused on developing more efficient algorithms for training and inference, as well as exploring new methods for ensuring model diversity.
CKA for Diversity#
The concept of using Centered Kernel Alignment (CKA) to enhance diversity in deep learning models, particularly within Bayesian frameworks, is a novel and insightful approach. CKA’s strength lies in its ability to measure the similarity between feature maps of different networks, overcoming limitations of simpler metrics that are not permutation invariant. The authors cleverly leverage CKA to encourage diversity within ensembles and hypernetworks by minimizing pairwise CKA scores. This is not without its challenges: directly optimizing CKA leads to vanishing gradients when networks become similar. The introduction of hyperspherical energy (HE) minimization as a refinement is crucial, addressing this gradient problem and promoting a more uniform distribution of models in the feature space. The integration of synthetic outliers and feature repulsion further enhances the method’s effectiveness. This approach contributes significantly to Bayesian deep learning by producing more diverse and reliable models, yielding improved uncertainty quantification and outlier detection capabilities. The combination of CKA and HE offers a powerful strategy for generating robust and informative deep learning ensembles. The application of this technique is particularly relevant to tasks demanding high uncertainty quantification and sensitivity to outliers.
Hyperspherical Energy#
The concept of “Hyperspherical Energy” in this context refers to a novel approach for promoting diversity in Bayesian deep learning ensembles. The core idea involves projecting kernel matrices representing network feature similarities onto a hypersphere, then minimizing the hyperspherical energy of these projected points. This addresses the limitation of traditional metrics that struggle with permutation invariance and diminishing gradients when networks are very similar. Minimizing hyperspherical energy encourages greater dispersion of networks across the hypersphere, leading to more diverse ensembles that improve uncertainty quantification, which is a crucial aspect of Bayesian deep learning. This method is particularly advantageous for complex models where traditional distance metrics are less effective. The use of hyperspherical energy represents a significant advance in generating diverse and robust deep learning ensembles, offering improved performance in challenging scenarios like outlier detection.
OOD Detection#
The research paper explores Out-of-Distribution (OOD) detection, a crucial aspect of robust machine learning. A key focus is on enhancing the uncertainty quantification capabilities of deep learning models, particularly within ensemble and hypernetwork settings. The authors introduce a novel approach leveraging hyperspherical energy (HE) minimization with centered kernel alignment (CKA) to promote diversity among network functions. This diversity improves the model’s ability to identify when an input sample falls outside the distribution it was trained on, resulting in improved OOD detection performance. Experiments on multiple datasets and network architectures demonstrate the effectiveness of the proposed method, showcasing its superiority to existing techniques across various scenarios. The use of synthetic OOD data and feature repulsion techniques further refines the approach, enhancing discrimination between in-distribution and out-of-distribution samples. The overall work suggests a significant advance in OOD detection, offering a more reliable and accurate method for determining the confidence of predictions made by deep learning models.
Future Work#
Future research directions stemming from this work on enhancing diversity in Bayesian deep learning could focus on several key areas. Automating hyperparameter selection (gamma, beta, and layer weights) is crucial for broader applicability. The current method requires manual tuning, limiting ease of use. Exploring alternative kernel functions beyond the HE-CKA, potentially incorporating invariance to other transformations (besides permutations), could improve performance. Investigating the impact of different smoothing techniques and their effect on training stability is also warranted. Furthermore, a more thorough exploration of the interaction between HE-CKA and the number of particles/batch size is needed to optimize performance across varied datasets and network architectures. Finally, applying this approach to different types of Bayesian inference and extending its use to other machine learning tasks beyond uncertainty quantification are promising avenues for future work. Specifically, research into how this method contributes to robustness in adversarial settings or improved transfer learning would be invaluable.
More visual insights#
More on figures

This figure compares the results of minimizing cosine similarity and hyperspherical energy (HE) on a unit hypersphere. Panel (a) shows the initial random distribution of points on the sphere. Panels (b) and (c) display the final point distributions after 50 iterations of optimization using cosine similarity and HE, respectively. The visualizations highlight how HE promotes a more uniform distribution of points, unlike cosine similarity which leads to clustering. Panels (d) and (e) plot the values of cosine similarity and HE, respectively, against the number of iterations during the optimization process, demonstrating HE’s faster convergence and achievement of uniformity.
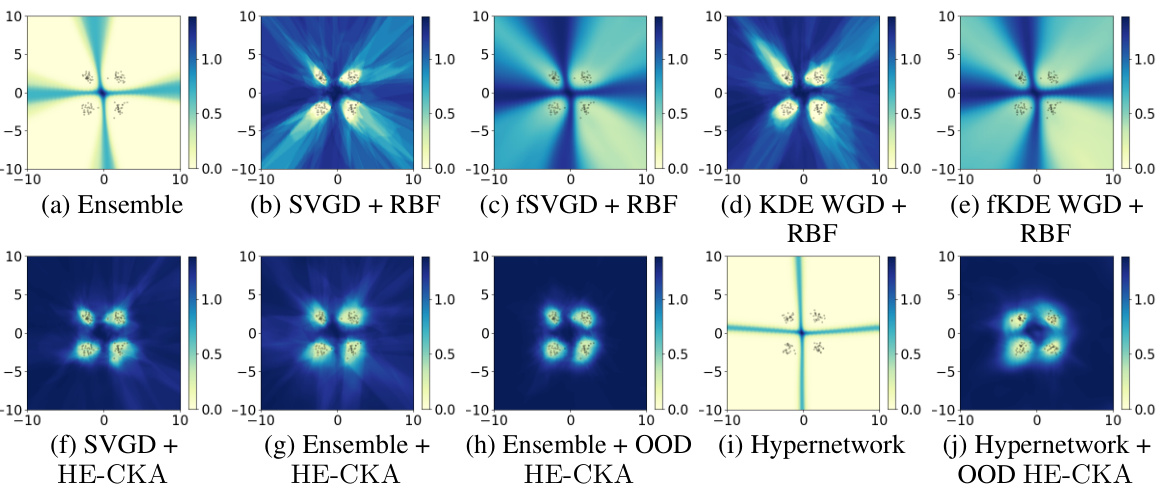
This figure compares the predictive entropy on a 2D four-class classification task using different methods: ensembles, SVGD with RBF kernel, and HE-CKA with and without OOD terms. Each subfigure shows a heatmap representing the predictive entropy, with darker colors indicating higher entropy (lower confidence) and lighter colors indicating lower entropy (higher confidence).
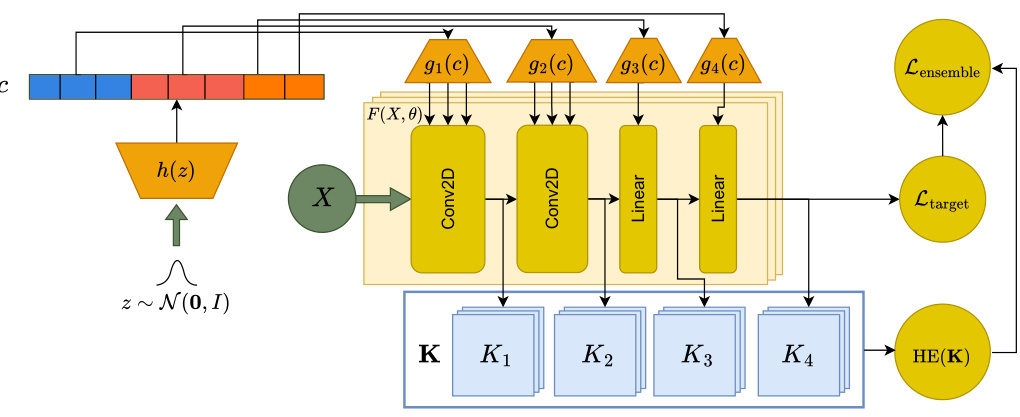
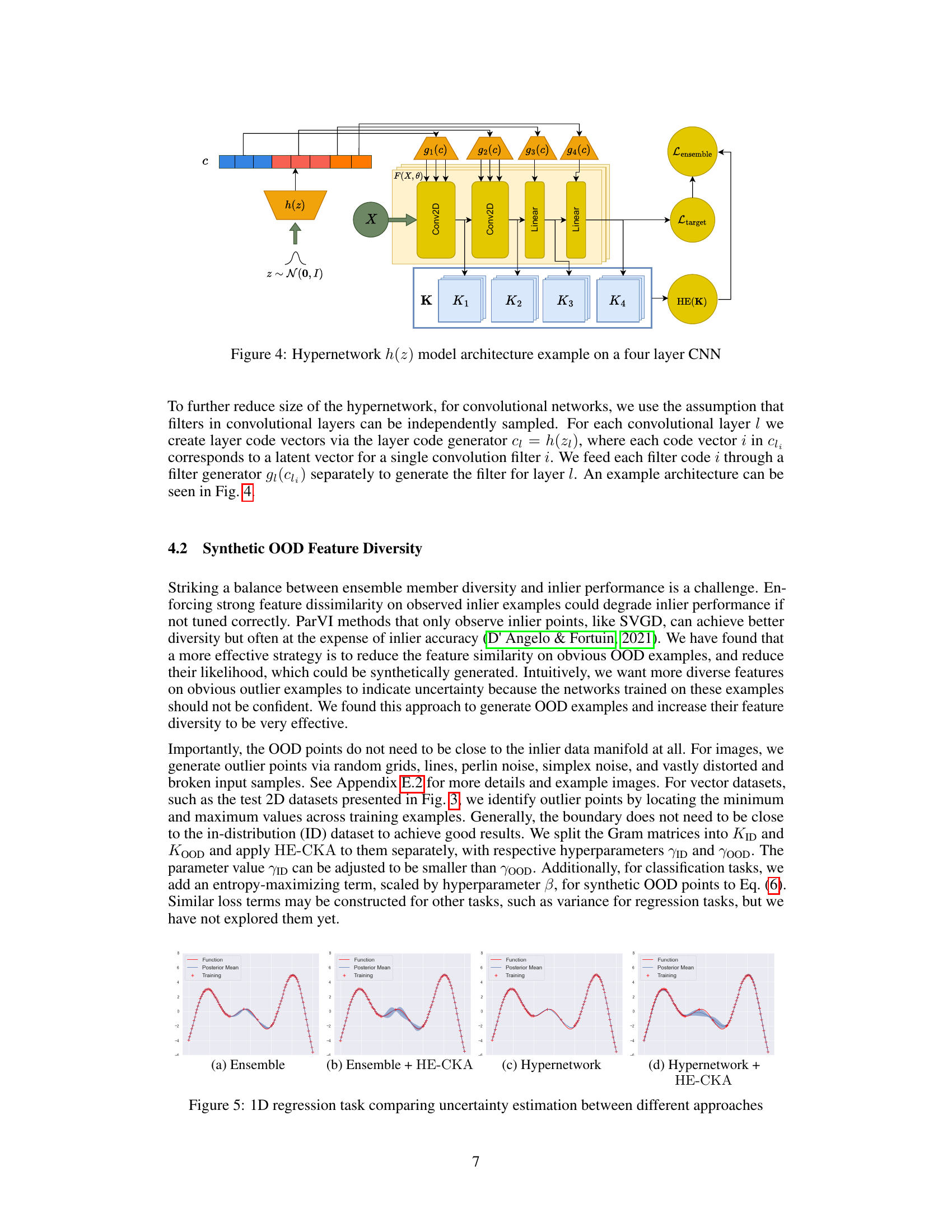
This figure illustrates the architecture of a hypernetwork used to generate the weights of a four-layer convolutional neural network (CNN). A latent vector z, sampled from a normal distribution N(0,I), is passed through the hypernetwork h(z). The output of the hypernetwork, denoted by c, is then used as input to four separate layer generators, g1(c), g2(c), g3(c), and g4(c). Each layer generator produces the weights for its corresponding layer in the CNN. The weights generated by the hypernetwork are used to make predictions on input data X. The features from each layer are then used to construct kernel matrices, which are in turn used to calculate the hyperspherical energy (HE).

The figure compares the uncertainty estimation of four different methods on a 1D regression task: (a) Ensemble, (b) Ensemble + HE-CKA, (c) Hypernetwork, and (d) Hypernetwork + HE-CKA. The x-axis represents the input values, and the y-axis represents the output values. The red line represents the true function, the blue shaded area represents the posterior mean, and the red plus signs represent the training data. The figure shows that adding HE-CKA to both ensembles and hypernetworks improves uncertainty estimation, especially in regions with low data density.
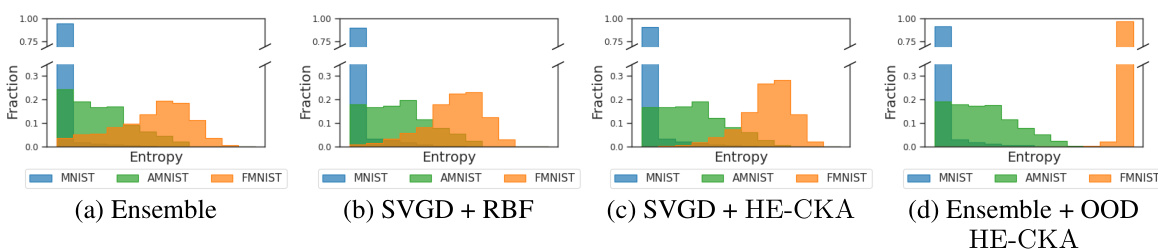
This figure shows the predictive softmax entropy for three different datasets: MNIST, Dirty-MNIST (MNIST with added noise representing aleatoric uncertainty), and Fashion-MNIST (out-of-distribution data). The results are shown for four different methods: a standard ensemble, SVGD with an RBF kernel, SVGD with HE-CKA, and an ensemble with HE-CKA and an OOD term. The HE-CKA methods, especially when combined with the OOD term, show significantly better separation between the in-distribution (Dirty-MNIST) and out-of-distribution (Fashion-MNIST) data. This illustrates the improved uncertainty quantification achieved by incorporating HE-CKA and the OOD term.

This figure shows the effect of the smoothing term ((\epsilon_{arc})) on the HE-CKA kernel’s performance when used with SVGD. As (\epsilon_{arc}) increases from 0.010 to 0.030, the resulting distribution of points on the hypersphere changes. Smaller values lead to more concentrated clusters, while larger values encourage a more uniform distribution. The smoothing term helps to manage the gradients during optimization, preventing the model from getting stuck in local optima. The plot shows that with increasing values of (\epsilon_{arc}), the distribution of points becomes more uniform, suggesting that the smoothing term is effective in improving the performance of the algorithm.

This figure compares the predictive entropy of various Bayesian deep learning methods on a 2D four-class classification task. Each subplot shows a heatmap representing the predictive entropy, with darker colors indicating higher entropy (lower confidence) and lighter colors indicating lower entropy (higher confidence). Different methods are compared, including those using RBF kernels on weights or outputs, and methods incorporating HE-CKA and OOD entropy terms. The figure demonstrates that incorporating diversity in the ensemble significantly improves uncertainty estimation.

This figure compares the predictive entropy from different methods on a synthetic 2D four-class classification task. It shows how different methods generate different levels of uncertainty in different regions. The results highlight the effectiveness of HE-CKA in improving uncertainty quantification compared to baselines.

This figure shows a 5x5 grid of images that are generated as out-of-distribution (OOD) examples for the CIFAR dataset. These images are synthetically generated using various transformations and augmentations to make them different from the in-distribution images. The purpose of using these synthetic OOD examples is to enhance the diversity of features in the ensemble of neural networks.

This figure illustrates the process of constructing a feature repulsive loss for enhancing diversity in deep learning ensembles. It shows how ensemble features from each layer are used to compute centered Gram matrices, which are then projected onto a unit hypersphere. The hyperspherical energy (HE) between the models on the hypersphere is then computed and incorporated into the loss function, along with inlier and outlier loss terms. Synthetic outliers are optionally included to help push models apart in feature space.

This figure visualizes predictive entropies on a 2D four-cluster classification task using different methods. Darker colors represent higher entropy (lower confidence), while lighter colors indicate lower entropy (higher confidence). It compares various methods such as ensembles, SVGD with RBF kernels on weights or outputs, and the proposed HE-CKA method, with and without out-of-distribution (OOD) data and entropy terms. The results show that HE-CKA with OOD terms can better estimate uncertainty and identify confidence regions effectively.
This figure compares predictive entropy for different methods on a 2D four-class classification task. It shows that HE-CKA significantly improves uncertainty estimation, especially when combined with out-of-distribution (OOD) entropy terms. The results demonstrate improved uncertainty quantification in low-density regions of the feature space.
This figure compares predictive entropy visualizations for different methods on a 2D four-cluster classification task. It shows how different methods (ensemble, SVGD with different kernels, HE-CKA with and without OOD) handle uncertainty estimation by visualizing the entropy in the feature space. Darker colors represent higher entropy and lower confidence, while lighter colors show lower entropy and higher confidence. The results highlight the superior uncertainty quantification achieved by the proposed HE-CKA approach, particularly when incorporating out-of-distribution (OOD) data.
The figure shows the predictive entropies of different methods on a four-cluster 2D classification task. Darker colors represent higher entropy (less confidence), while lighter colors represent lower entropy (higher confidence). The figure compares several methods, highlighting the impact of different kernels (RBF vs. HE-CKA) and the inclusion of out-of-distribution (OOD) data and entropy terms. The results demonstrate the improved uncertainty estimation by the proposed method (HE-CKA) across diverse model ensembles.
This figure compares the predictive entropy results of different methods on a 2D four-cluster classification task. It illustrates how different methods (ensemble, SVGD with RBF kernel, SVGD with HE-CKA kernel, etc.) produce different uncertainty estimations, visualized as heatmaps. Darker colors represent higher uncertainty (lower confidence), and lighter colors show lower uncertainty (higher confidence). The impact of using an RBF kernel on weights vs. outputs, and the effect of adding HE-CKA and out-of-distribution (OOD) terms are shown.

This figure compares the predictive entropy of different methods on a 2D four-cluster classification task. Each subfigure shows the predictive entropy for a different approach: ensemble methods, SVGD with RBF kernel (on weights and outputs), KDE with RBF kernel, and finally, the proposed method HE-CKA with and without OOD examples. Darker colors mean higher entropy (lower confidence), illustrating the effectiveness of HE-CKA in uncertainty quantification.
This figure compares different methods’ uncertainty estimation performance on a 2D four-cluster classification task. The color intensity represents predictive entropy, with darker shades indicating higher entropy (uncertainty) and lighter shades indicating lower entropy (certainty). The results show that using HE-CKA, along with OOD entropy terms, improves the accuracy of the uncertainty estimations. Different kernels (RBF on weights vs. outputs) and the inclusion of out-of-distribution (OOD) data are also considered.
This figure compares predictive entropy of different methods on a 2D four-cluster classification task. The darker the color, the higher the entropy (uncertainty), and lighter colors indicate higher confidence. It shows the effect of using different kernels (RBF, HE-CKA) and incorporating out-of-distribution (OOD) examples on uncertainty estimation. The results illustrate the improvement in uncertainty quantification provided by the proposed HE-CKA method, especially when combined with OOD examples.
More on tables
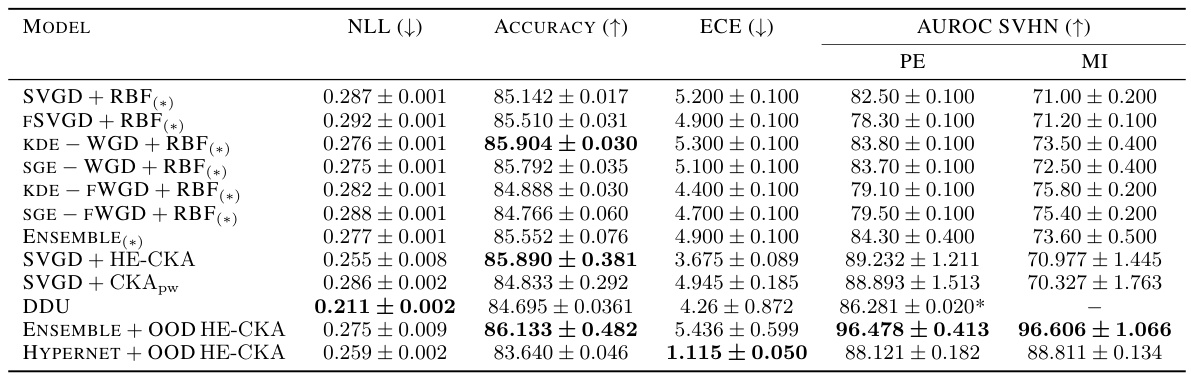
This table presents the out-of-distribution (OOD) detection results on CIFAR-10 versus SVHN datasets. Different methods are compared, including variations of Stein Variational Gradient Descent (SVGD) with different kernels (RBF, CKApw, HE-CKA), Deep Deterministic Uncertainty (DDU), and ensembles. The table shows negative log-likelihood (NLL), accuracy, expected calibration error (ECE), area under the receiver operating characteristic curve (AUROC) for SVHN (as the OOD dataset), predictive entropy (PE), and mutual information (MI). The results highlight the performance of the proposed HE-CKA method in improving OOD detection capabilities compared to other approaches.

This table presents the results of out-of-distribution (OOD) detection experiments using the Dirty-MNIST dataset as inliers and Fashion-MNIST as outliers. Multiple models, including a deep ensemble, SVGD with various kernel choices (RBF, CKApw, HE-CKA), and a hypernetwork, were evaluated. Performance is measured by negative log-likelihood (NLL), accuracy, expected calibration error (ECE), AUROC on Fashion-MNIST, predictive entropy (PE), and mutual information (MI). The HE-CKA method shows better performance, especially when combined with out-of-distribution (OOD) examples, leading to near-perfect OOD detection.
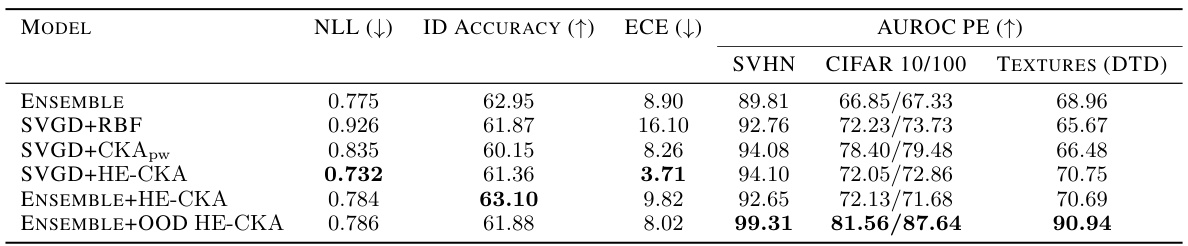
This table presents the results of out-of-distribution (OOD) detection experiments using a five-member ResNet18 ensemble trained on the TinyImageNet dataset. The models were initially pretrained without a repulsive term, then fine-tuned for 30 epochs using various methods. These include a standard ensemble, SVGD with RBF, CKApw, and HE-CKA kernels. The table displays negative log-likelihood (NLL), in-distribution (ID) accuracy, expected calibration error (ECE), and area under the receiver operating characteristic curve (AUROC) for predictive entropy (PE) on SVHN, CIFAR-10/100, and Textures (DTD) datasets. The HE-CKA and CKApw methods used a linear feature kernel.

This table presents the out-of-distribution (OOD) detection results on the CIFAR-100 dataset using SVHN as the outlier dataset. Three different model variations were tested: a standard ensemble, an ensemble with HE-CKA regularization, and an ensemble with HE-CKA regularization and synthetic OOD data. The results show negative log-likelihood (NLL), accuracy on in-distribution data, expected calibration error (ECE), and area under the receiver operating characteristic curve (AUROC) for SVHN as an outlier. The metrics evaluate the performance of each model variation in distinguishing between in-distribution and out-of-distribution samples.

This table presents the results of an ablation study on the number of particles used in training a ResNet18 model with the HE-CKA method on the TinyImageNet dataset. The table shows that increasing the number of particles generally improves performance, as measured by negative log-likelihood (NLL), ID accuracy, expected calibration error (ECE), and AUROC of the predictive entropy (PE) for outlier detection on SVHN, CIFAR-10/100, and Textures (DTD) datasets. The best performance is observed when using 5 particles.
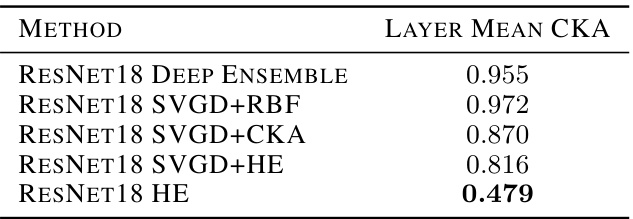
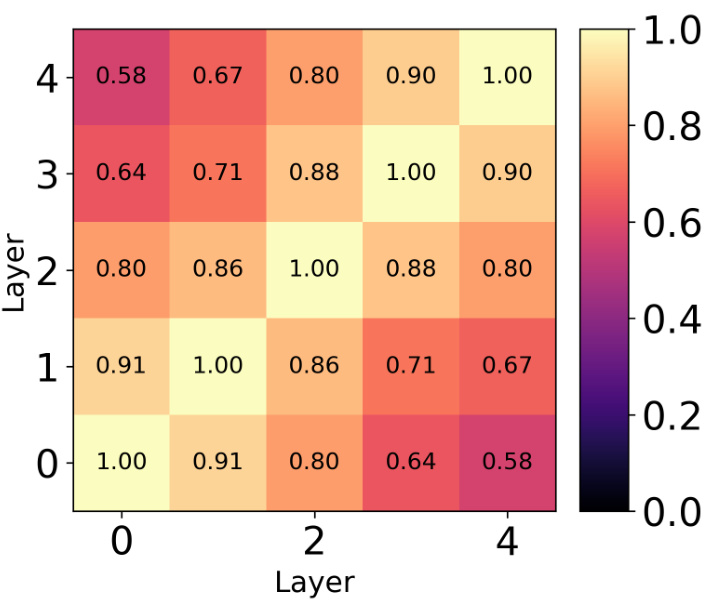
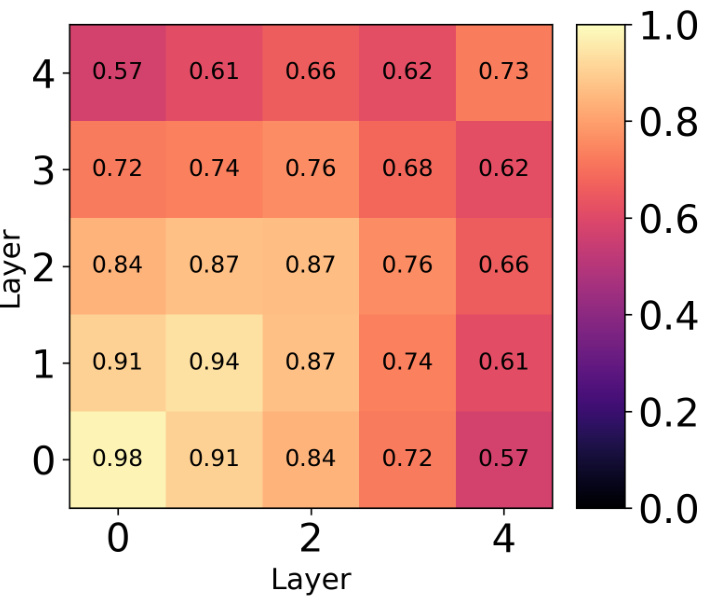
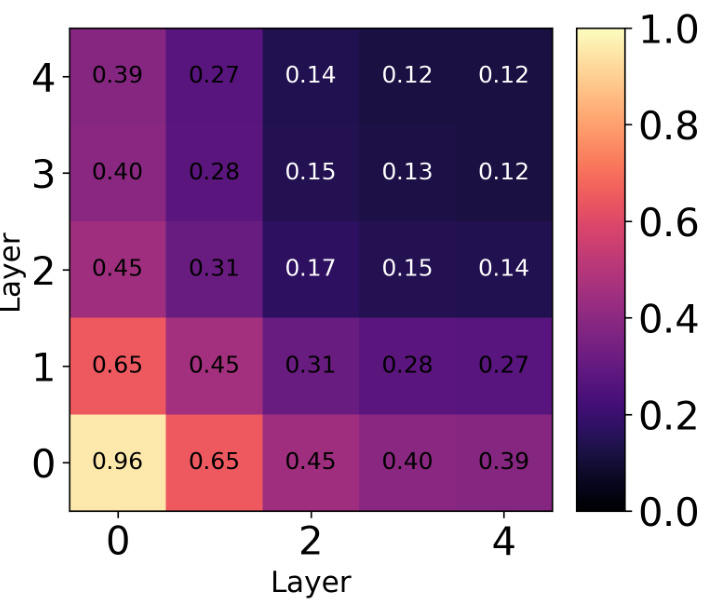
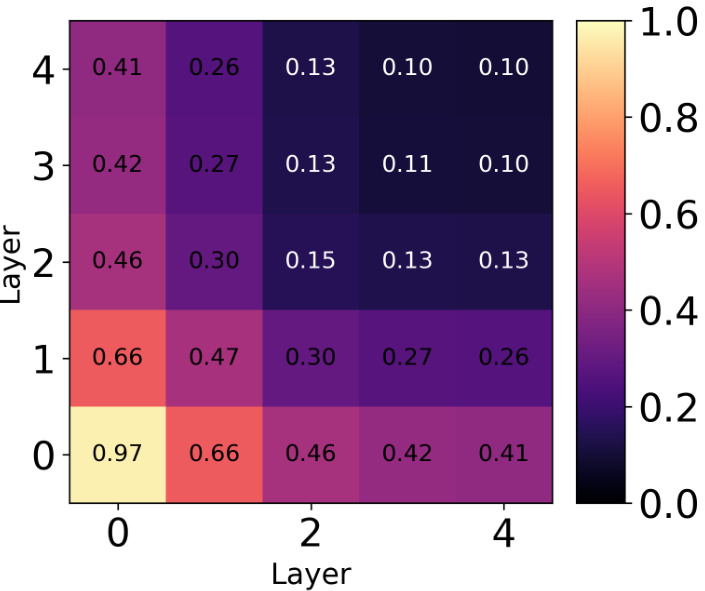
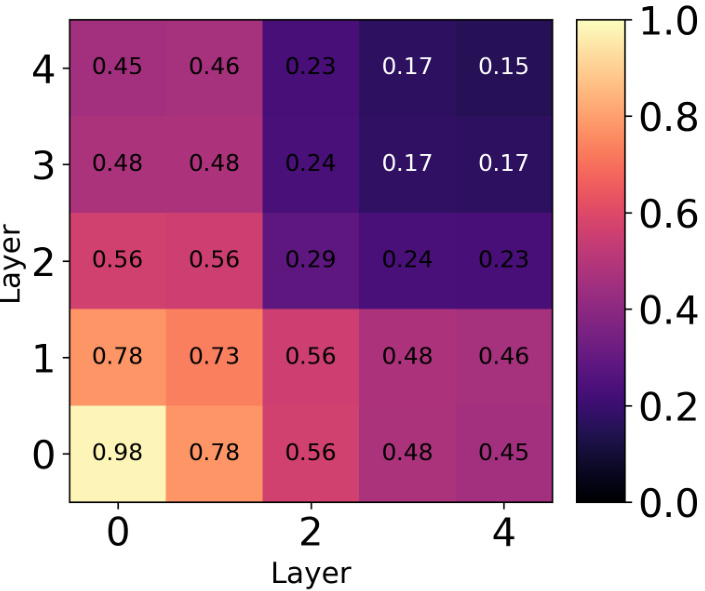
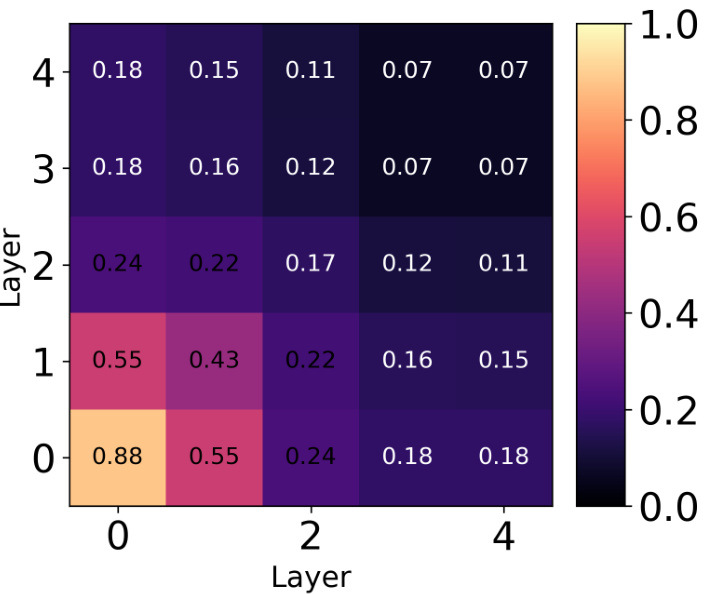
This table shows the average pairwise unbiased Centered Kernel Alignment (CKA) values across all layers for different methods used to train an ensemble of 5 ResNet18 models on the CIFAR-10 dataset. The methods compared include a standard deep ensemble, SVGD with RBF kernel, SVGD with CKA regularization, SVGD with hyperspherical energy (HE) regularization, and HE alone. Lower CKA values indicate greater diversity among the models in the ensemble.

This table presents the out-of-distribution (OOD) detection performance of various methods on the Dirty-MNIST and Fashion-MNIST datasets. It compares the Negative Log-Likelihood (NLL), Accuracy, Expected Calibration Error (ECE), Area Under the Receiver Operating Characteristic curve (AUROC) for Fashion-MNIST, predictive entropy (PE), and mutual information (MI). The results are averaged over 5 runs and show that the proposed HE-CKA method outperforms other baselines, especially when combined with out-of-distribution (OOD) data and entropy terms.
Full paper#