↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) with general function approximation faces challenges in balancing efficient exploration and exploitation, especially when frequent policy updates are expensive. Existing algorithms often struggle with either high regret (poor performance) or high switching costs. This limits their applicability in real-world scenarios.
The proposed MQL-UCB algorithm tackles these issues by using a novel deterministic policy-switching strategy that minimizes updates. It also incorporates a monotonic value function structure and a variance-weighted regression scheme to improve data efficiency. MQL-UCB achieves a minimax optimal regret bound and near-optimal policy switching cost, demonstrating significant advancements in sample and deployment efficiency for RL with nonlinear function approximations.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents a novel algorithm, MQL-UCB, that achieves near-optimal regret and low policy switching cost in reinforcement learning with general function approximation. This addresses a key challenge in real-world applications where deploying new policies frequently is costly. The work also provides valuable theoretical insights into algorithm design and performance bounds, paving the way for more efficient and practical RL algorithms.
Visual Insights#
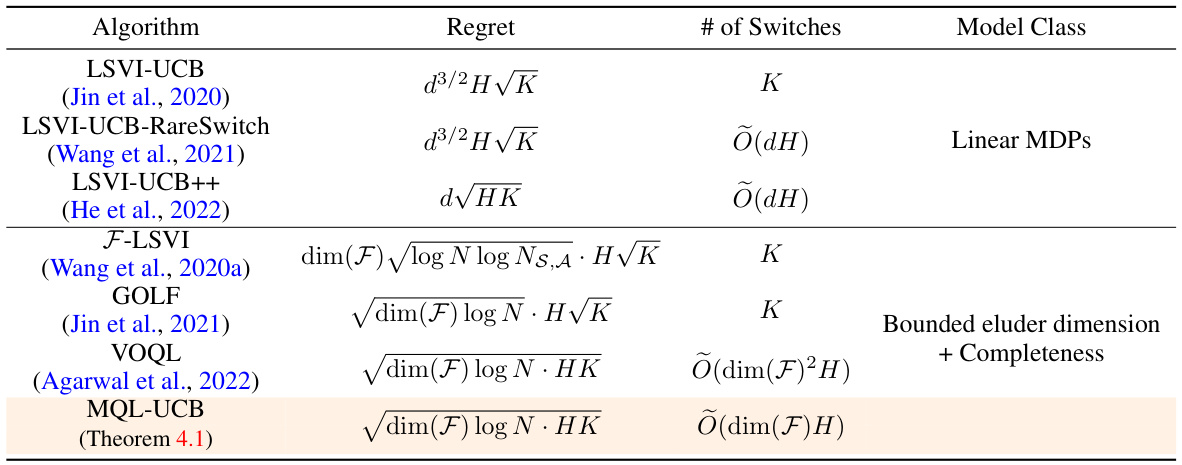
This table compares various reinforcement learning algorithms across several key metrics: regret (the difference between the cumulative reward of the optimal policy and the algorithm’s policy), switching cost (how often the algorithm changes its policy), and the type of model class they are applicable to (linear MDPs or general function classes with bounded eluder dimension and Bellman completeness). The regret bounds presented are simplified, showing only the leading terms and ignoring polylogarithmic factors. For general function classes, the table uses the eluder dimension (dim(F)), covering numbers (N, Ns,A) and other parameters to quantify the regret and switching cost.
Full paper#



















