↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Randomized smoothing is a popular technique to certify the robustness of machine learning models against adversarial attacks, however it is computationally expensive. The existing methods require many classifier passes, making it slow and impractical. This paper addresses the problem of statistical estimation in randomized smoothing which is the bottleneck of the algorithm.
The authors propose improvements to the existing methods, including using confidence sequences instead of confidence intervals, which enable adaptive and more efficient estimation. They also developed a new version of Clopper-Pearson confidence intervals and provided a complete theoretical analysis proving their optimality and demonstrating their improved performance empirically.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in adversarial robustness and machine learning because it significantly improves the efficiency of randomized smoothing, a leading certification method. By introducing novel statistical estimation techniques, this work reduces the computational cost of verifying robustness, making certified defenses more practical for real-world applications. It also opens up new avenues for adaptive estimation, impacting other areas beyond randomized smoothing.
Visual Insights#

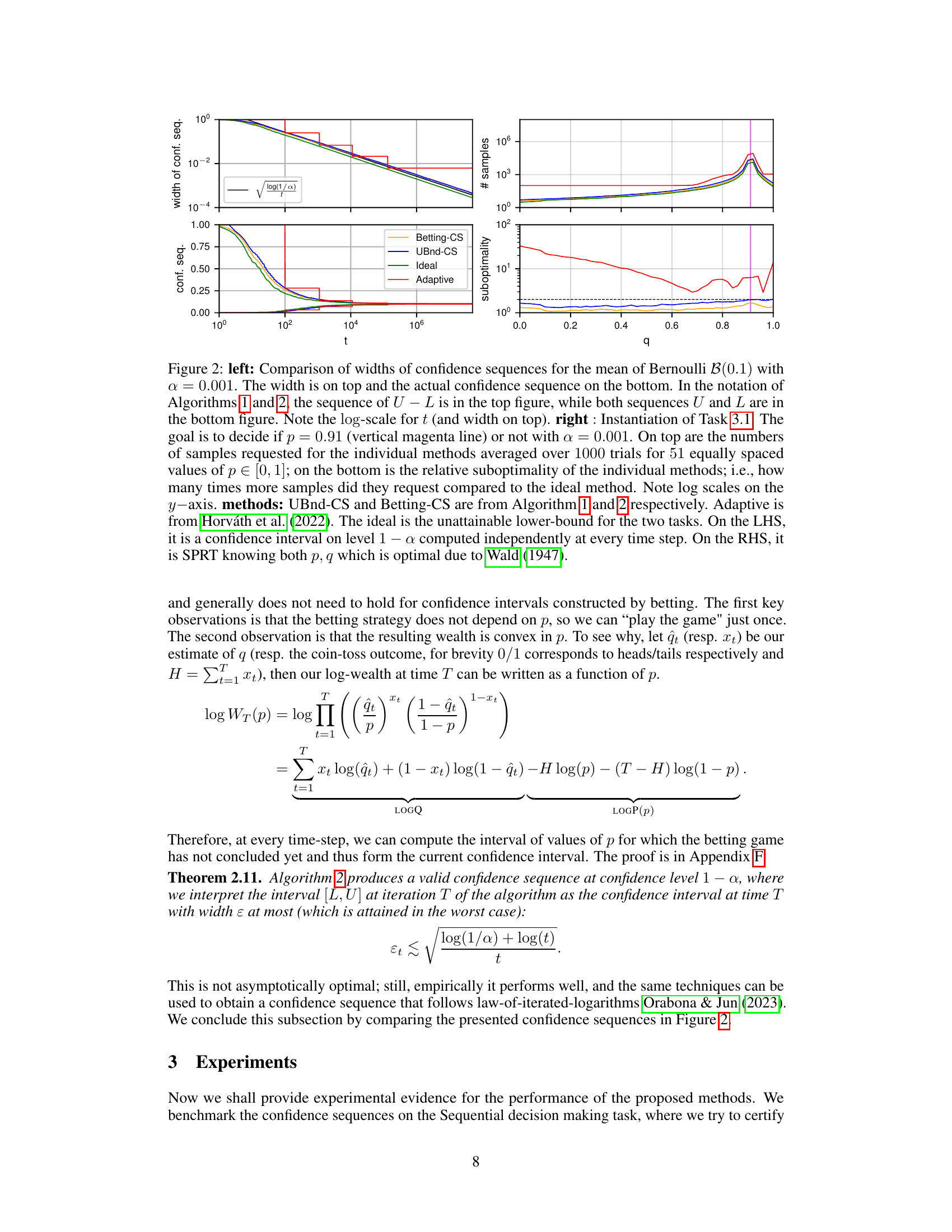
The left plot compares the actual coverage of the Clopper-Pearson and Randomized Clopper-Pearson confidence intervals for estimating the mean of a binomial distribution B(100,p) with a confidence level of 1-α=0.999. It shows that the randomized version has better coverage properties, particularly for larger values of p. The right plot shows the robustness curves for a CIFAR-10 dataset obtained using the standard and the randomized Clopper-Pearson methods. The randomized method yields stronger certificates (higher robustness).
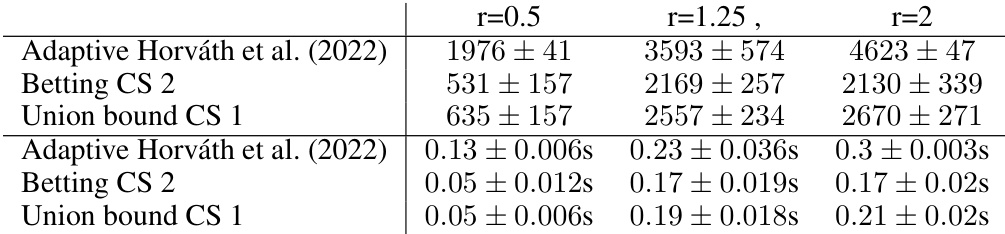
This table compares three different methods for certifying the robustness of a point at different radii. The methods compared are Adaptive Horváth et al. (2022), Betting CS 2, and Union bound CS 1. For each method and radius, the table shows the average number of samples required and the average time needed to reach a decision. The results are for the CIFAR-10 dataset and the l2 norm.
In-depth insights#
RS Conf. Seq.#
The heading ‘RS Conf. Seq.’ likely refers to a method combining randomized smoothing (RS) with confidence sequences for improved robustness certification in machine learning models. Randomized smoothing is a popular technique for certifying adversarial robustness by adding noise to the input, but it’s computationally expensive. Confidence sequences offer a sequential approach to statistical estimation, allowing for adaptive sampling. This combination aims to reduce the computational cost of randomized smoothing by only using as many samples as necessary to provide the desired level of certification, thus improving efficiency. The approach likely leverages the statistical guarantees of confidence sequences to provide stronger certificates of robustness, reducing the false positive rate of claiming robustness. Optimality might be explored by comparing the number of samples used to existing methods, demonstrating improved sample efficiency. The use of confidence sequences represents a significant improvement over traditional confidence intervals which are often conservative and require pre-determined sample sizes.
Improved CPIs#
The concept of “Improved CPIs” likely refers to enhancements made to Clopper-Pearson confidence intervals (CPIs). CPIs are a standard method for constructing confidence intervals for binomial proportions, but they are known to be conservative, meaning they often produce wider intervals than necessary. This can reduce statistical power, making it harder to detect true effects. Improvements could involve developing more accurate methods that better approximate the true coverage probability, perhaps employing techniques like randomization or transformations to reduce the conservativeness. Another area of improvement could be on computational efficiency; CPIs can be computationally intensive, particularly for large sample sizes, making faster algorithms a desirable improvement. Finally, improved CPIs might aim to provide more flexible or adaptive methods. For example, they might accommodate different types of prior information or allow for sequential updating of the intervals as more data are acquired. The overall goal of “Improved CPIs” would likely be to increase the precision and efficiency of confidence interval estimation while maintaining or improving the desired confidence level. Such improvements would have broad applications in statistical inference wherever binomial data are analyzed.
Adaptive Cert.#
The concept of “Adaptive Cert.” in the context of adversarial robustness likely refers to adaptive certification methods that dynamically adjust their parameters or sampling strategies based on the input data and model behavior. This contrasts with traditional, static certification, which uses fixed parameters across all inputs. Adaptive certification offers the potential for increased efficiency by avoiding unnecessary computation for easily certifiable points, and improved accuracy by adapting to the specific challenges posed by harder-to-certify examples. However, adaptive methods raise new challenges, requiring careful consideration of statistical guarantees and sample complexity to ensure reliable and valid certificates. A key research direction would be to design adaptive certification that balances computation with certification quality, formally demonstrating superior performance over static approaches while maintaining strong statistical guarantees and avoiding overfitting to specific training data.
Betting Approach#
The core idea of the betting approach in the context of confidence sequences involves framing the statistical estimation problem as a hypothetical betting game. Each hypothesis (a specific value of the parameter being estimated) corresponds to a fair betting game, designed such that the gambler’s wealth remains constant in expectation if the hypothesis is true. However, if the hypothesis is false, strategic betting can lead to exponential wealth growth. The betting strategy itself is crucial; it should adapt to the observed data, ideally maximizing the expected logarithmic wealth (Kelly Criterion). By observing the evolution of wealth across multiple games, corresponding to various hypotheses, those hypotheses with insufficient wealth growth can be eliminated, effectively constructing a confidence sequence that shrinks over time. This method offers a compelling alternative to traditional methods like union bounds, potentially leading to tighter confidence sequences and improved sample efficiency, particularly for sequentially updated confidence regions. The key advantage lies in the ability to adaptively adjust the sample size, only drawing as many samples as are strictly necessary for the desired confidence level. However, it is important to carefully consider the design of the betting game and betting strategy, ensuring fairness and optimality to guarantee the method’s effectiveness.
Future Works#
Future research directions stemming from this work on randomized smoothing could explore several avenues. Improving the efficiency of confidence sequence methods is crucial; reducing computational costs is key to making these techniques practical for real-world applications. Investigating alternative smoothing distributions beyond the Gaussian or uniform distributions currently explored could enhance robustness against specific attack types. The work’s focus on adaptive sampling suggests a promising path, and future work could develop and analyze more sophisticated adaptive strategies, potentially incorporating Bayesian methods. Finally, extending the framework to a wider range of machine learning tasks and model architectures beyond image classification would broaden its applicability and impact, including, for example, natural language processing or time-series analysis.
More visual insights#
More on figures

The left plot compares the coverage of standard and randomized Clopper-Pearson confidence intervals for estimating the mean of a binomial distribution B(100,p) with a confidence level of 1-0.001. It shows that the standard Clopper-Pearson interval is conservative, especially for larger values of p, while the randomized version achieves the desired coverage. The right plot illustrates the effect of using these different confidence intervals in the context of randomized smoothing for certifying the robustness of a classifier on the CIFAR-10 dataset. The randomized Clopper-Pearson interval leads to a more accurate and less conservative estimate of the robustness radius, overcoming the sharp drop usually observed at the end of the robustness curve in standard methods.
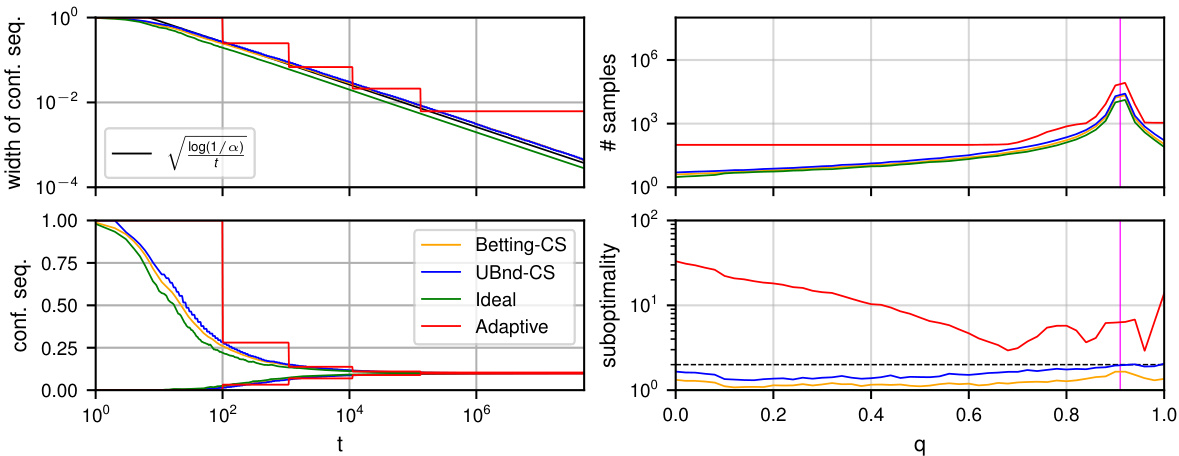
This figure compares the performance of different confidence sequence methods for estimating the mean of a Bernoulli distribution. The left panel shows the width of the confidence sequences over time, demonstrating the efficiency of the proposed methods. The right panel illustrates the number of samples required by each method to make a decision in a sequential decision-making task, highlighting the optimality of the proposed methods compared to existing techniques.
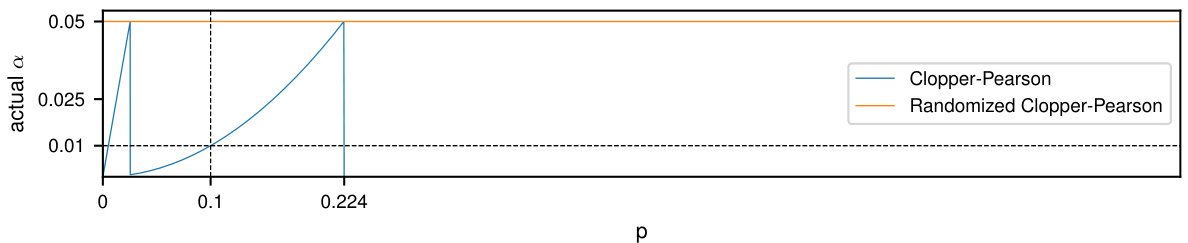
This figure compares the actual coverage of the standard Clopper-Pearson confidence intervals and the randomized version for a binomial distribution with parameters n=2 and varying p. The x-axis represents the probability of success p, while the y-axis represents the actual coverage, which is the probability that the confidence interval contains the true value of p. The dashed line represents the desired coverage level of 1-α = 0.95. The plot shows that the standard Clopper-Pearson intervals are conservative, meaning they overcover; their actual coverage is always greater than or equal to the desired coverage level. In contrast, the randomized Clopper-Pearson intervals achieve the desired coverage level, making them more efficient.

This figure compares the robustness curves obtained using binary and multiclass certification methods. In the binary case, the entire error budget is allocated to controlling the probability of the top class. In contrast, the multiclass method divides the error budget between controlling the top class probability and the second-highest class probability. The results show that multiclass certification achieves a higher average certified radius than binary certification. This indicates that the multiclass approach may be more effective in certifying the robustness of classifiers.
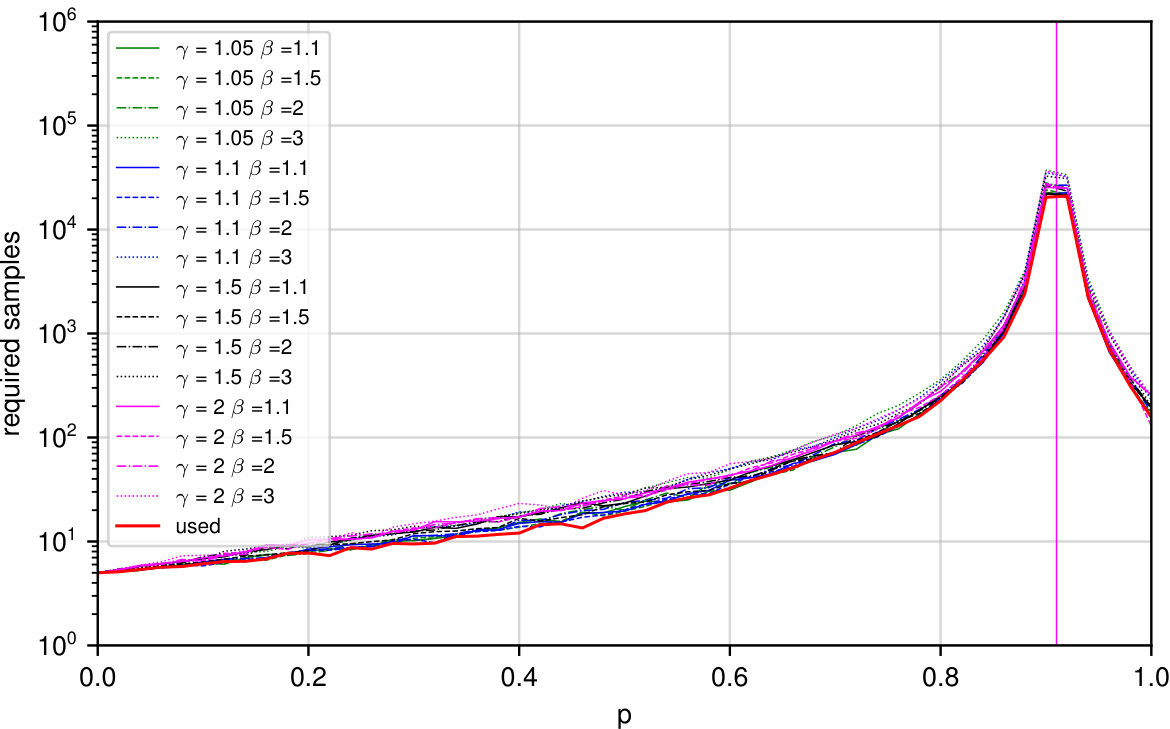
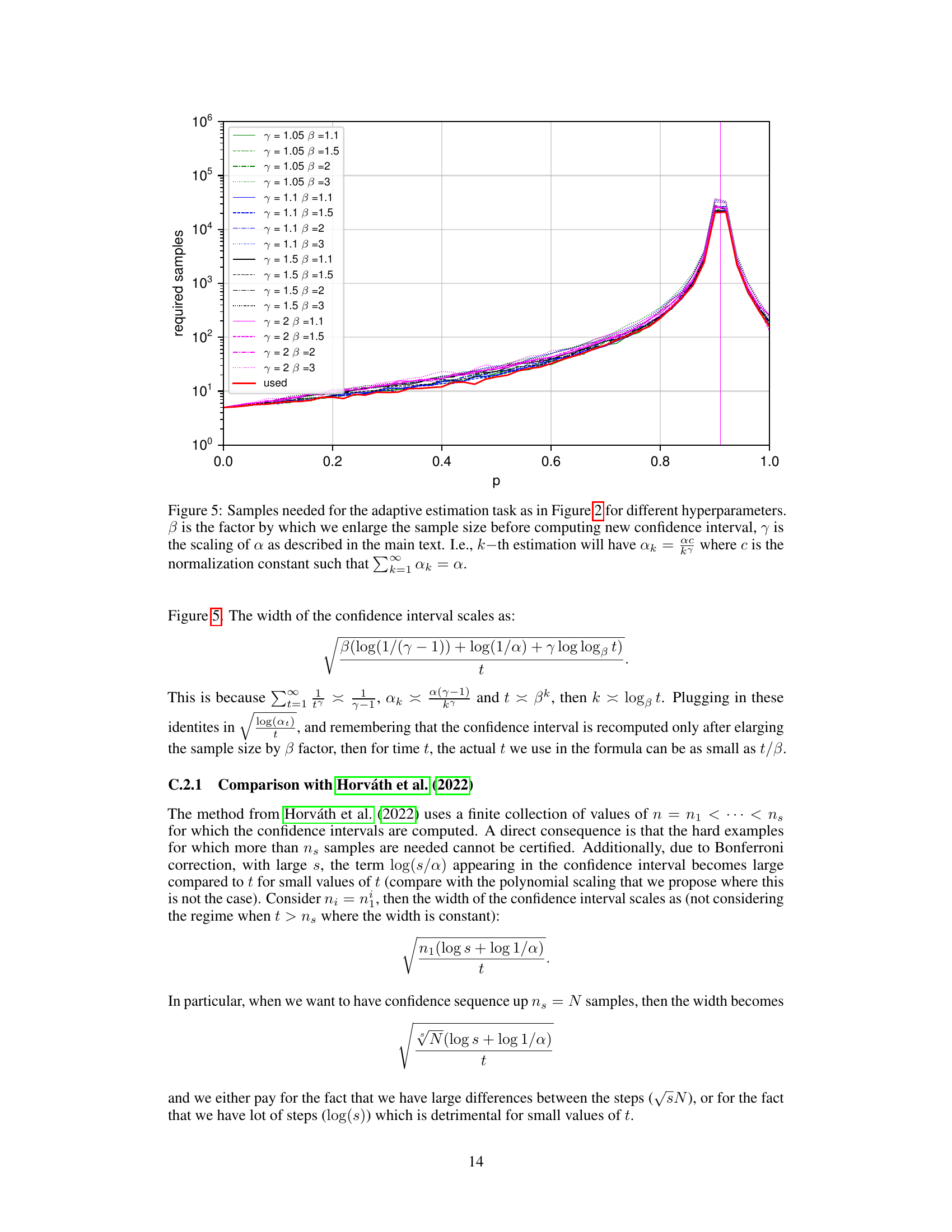
This figure compares the number of samples required by different confidence sequence algorithms for the sequential decision-making task. The x-axis represents the true probability (p), and the y-axis shows the number of samples needed. Different lines represent different algorithms, parameterized by γ (controls the decay rate of the failure probability) and β (controls how often the confidence interval is recomputed). The red line (‘used’) indicates the actual number of samples used by the algorithm, showing that the adaptive estimation procedures are more efficient compared to non-adaptive ones.
More on tables
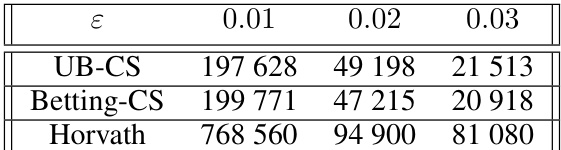
This table compares the average number of samples required by three different methods (UB-CS, Betting-CS, and Horvath) to certify a certain radius, given a confidence level of 0.999 and different values of ε (error margin). The experiment uses a WideResnet-40 network trained on CIFAR10 with a standard deviation (σ) of 1. The results highlight the efficiency gains of the confidence sequence methods (UB-CS and Betting-CS) compared to the Horvath method, which requires significantly more samples.

This table compares three different methods for certifying the robustness of a point at different radii. The methods are Adaptive Horváth et al. (2022), Betting CS 2, and Union bound CS 1. The table shows the average number of samples required to make a decision, along with the standard deviation, for each method and radius. It also shows the average time taken. The results indicate that Betting CS 2 and Union bound CS 1 require significantly fewer samples than Adaptive Horváth et al. (2022) to achieve the same level of certification.
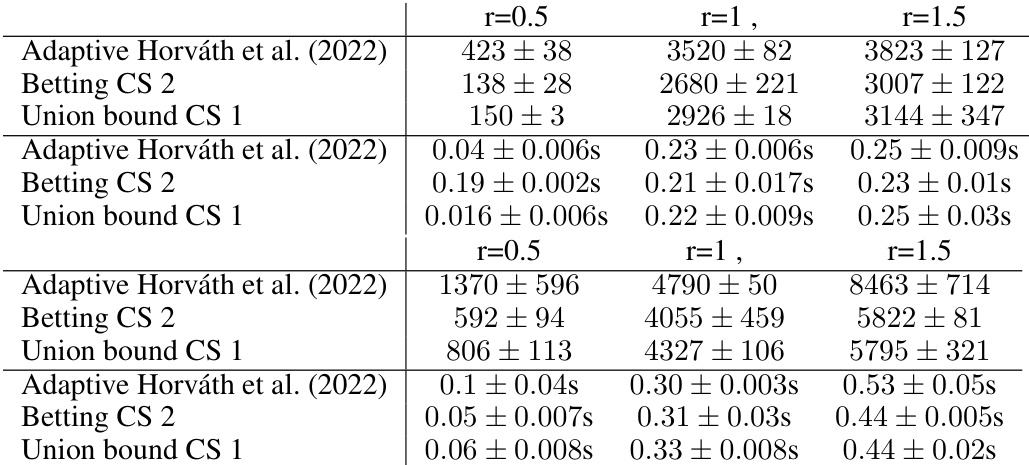
This table compares the performance of three different methods for certifying the robustness of a point at different radii (0.5, 1.25, and 2). The methods compared are: Adaptive Horváth et al. (2022), Betting CS 2, and Union bound CS 1. The table shows the average number of samples required to make a decision, along with the standard deviation, and the average time taken. The dataset used is CIFAR-10 with the l2 norm.
Full paper#