↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Event cameras offer advantages over traditional cameras but require specialized processing algorithms. Existing event-based vision models often lack efficiency and struggle with temporal modeling. This paper introduces Parametric Piecewise Linear Networks (PPLNs), inspired by biological neural mechanisms, to address these limitations.
PPLNs use piecewise linear functions to represent neural membrane potential, enabling efficient temporal modeling. Experiments show that PPLNs achieve state-of-the-art results in motion deblurring, steering prediction, and human pose estimation, outperforming existing methods in both event-based and frame-based settings. The key is its bio-inspired design and efficient use of learnable parameters.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel neural network architecture for temporal data processing, particularly event-based data. It demonstrates state-of-the-art performance in several computer vision tasks, and the use of biologically inspired piecewise linear functions offers a fresh perspective on deep learning design. This could lead to more efficient and effective models for various time-series applications, including those dealing with neuromorphic sensors.
Visual Insights#
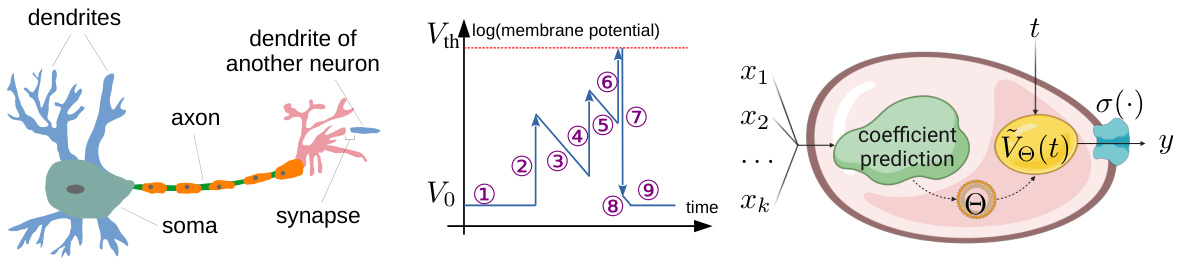
This figure shows a biological neuron’s components (dendrites, axon, soma, synapse), its membrane potential approximated by a piecewise linear function (illustrating resting state, external input, threshold excitation, spike generation, and decay), and the PPLN node, which uses input data (x1, x2,…xk) and time (t) to predict linear coefficients (Θ) for the membrane potential function (Ve(t)) resulting in output y.
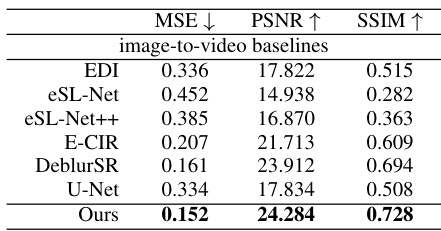
This table presents a comparison of motion deblurring and steering prediction results. The ‘Left’ side shows the mean squared error (MSE), peak signal-to-noise ratio (PSNR), and structural similarity index measure (SSIM) for various methods on motion deblurring. The ‘Right’ side shows the root mean square error (RMSE) and explained variance (EVA) for various methods on steering angle prediction, separated by day and night driving conditions and overall.
In-depth insights#
Neuromorphic Vision#
Neuromorphic vision, inspired by the biological visual system, offers a compelling alternative to traditional computer vision. Event-based cameras, mimicking the human retina’s asynchronous operation, capture only changes in visual data, leading to high temporal resolution and reduced power consumption. This contrasts sharply with frame-based cameras’ continuous data stream. Spiking neural networks (SNNs), designed to process the event-based data, offer biologically plausible computation that can be highly energy-efficient. However, SNNs present training challenges. The integration of parametric piecewise linear networks (PPLNs) offers a new approach that leverages the advantages of both event-based data and potentially more trainable deep networks. Bio-inspired deep learning models, such as PPLNs, aim to bridge the gap between biological mechanisms and deep learning algorithms for superior performance and efficiency in temporal vision tasks.
PPLN Architecture#
The core of the PPLNs lies in its novel architecture, which mimics biological neural processing. Parametric piecewise linear functions replace traditional activation functions at each node. This design allows the network to approximate the temporal evolution of a neuron’s membrane potential, a key aspect of biological neural computation often overlooked in standard deep learning models. The network uses learnable parameters to define the slope, intercept, and endpoints of the piecewise linear segments at each node, making it highly adaptable to diverse temporal input data. The use of input-dependent piecewise linear functions differentiates PPLNs from other approaches such as KANs (which use fixed B-splines), offering greater flexibility in capturing complex temporal dynamics. The combination of smoothing and integral normalization techniques enhances training stability and enables better handling of input heterogeneity. This architecture allows efficient temporal modeling and can easily integrate with existing deep network structures such as convolutional layers, resulting in state-of-the-art performance.
Event Data Modeling#
Event data modeling presents unique challenges and opportunities. The high-velocity, asynchronous nature of event streams necessitates specialized techniques beyond traditional time-series analysis. Representing event data effectively often involves considering dimensionality reduction and efficient data structures to manage the volume. Temporal modeling is crucial to capture the dynamic evolution of events and their relationships. Choosing appropriate models depends on the specific application and the inherent structure of the events. Neuromorphic principles often inform model design, particularly in domains like vision where event cameras mimic neural activity. The focus should be on learning meaningful representations that capture the temporal context while managing noise and sparsity. Real-time processing capabilities are highly desirable for many applications, driving the need for efficient and scalable models.
Vision Task Results#
A thorough analysis of the ‘Vision Task Results’ section requires a deep dive into the methodologies and metrics used to evaluate the performance of different vision tasks. Key aspects to examine include the specific vision tasks addressed (e.g., image classification, object detection, segmentation), the datasets employed for evaluation, and the performance metrics used (e.g., accuracy, precision, recall, F1-score, mAP). It’s crucial to assess whether the chosen datasets and metrics are appropriate and widely accepted within the field. Furthermore, a critical appraisal should consider the experimental setup, including training protocols, parameter tuning techniques, and the robustness of the results to variations in these factors. A comparison with state-of-the-art results on the same benchmarks is essential to determine the novelty and significance of the findings. Finally, the presentation and discussion of the results should be carefully evaluated for clarity, completeness, and fairness. Any limitations or potential biases should be acknowledged and their impact on the interpretation of the results should be discussed.
Future of PPLNs#
The future of Parametric Piecewise Linear Networks (PPLNs) appears bright, given their strong performance and bio-inspired design. Further research could focus on enhancing the network’s capacity to handle complex temporal dependencies by incorporating more sophisticated mechanisms for approximating membrane potentials, such as exploring different piecewise functions beyond linear. Investigating the integration of PPLNs with other neuromorphic computing architectures would also be a valuable direction, potentially leading to more efficient and powerful systems for processing event-based data. Exploring different training strategies and optimization techniques to address potential instability in training could improve the model’s robustness and generalization ability. Finally, applying PPLNs to a wider array of tasks beyond those presented in the original research would showcase their true potential and adaptability. The possibilities include applications in areas such as robotics, autonomous driving, and medical imaging, where precise temporal information is crucial.
More visual insights#
More on figures

This figure shows the architecture of the proposed Parametric Piecewise Linear Networks (PPLNs). Panel (a) illustrates a linear PPLN node, showing how input features (x) and a timestamp (t) are used to predict linear coefficients (m, b, s), which are then used to generate a piecewise linear function that produces the output (f). Panel (b) shows a similar 2D convolutional PPLN node, where the convolution operation is applied before coefficient prediction. Panels (c), (d), and (e) compare the proposed model to existing baselines for steering angle prediction. Panel (c) shows the original baseline, (d) the proposed model that uses PPLNs, and (e) a modified baseline with a similar number of input channels as the proposed model.

This figure displays a qualitative comparison of motion deblurring results from different methods. The top row shows the input blurry images, the ground truth sharp images, and results from various state-of-the-art deblurring methods, and the bottom row shows the results obtained by the proposed method (PPLNs). The images show that the proposed method produces sharper and more realistic results compared to the baseline methods.

This figure shows the results of motion deblurring using different methods on the HQF dataset. The first column shows the blurry input images, followed by the ground truth, and then the results from several methods, including EDI, eSL-Net, E-CIR, DeblurSR and the proposed method (Ours). The figure provides a visual comparison of the methods’ performance on diverse scenes.

This figure shows example piecewise linear functions produced by the network. The plots demonstrate the variety of functions the network can learn, including those with uneven segment lengths and discontinuities at segment boundaries, showing that the network does not collapse to a simple model.

This figure shows the impact of integral normalization on the ability of the model to fit piecewise linear signals with varying segment lengths. The left panel shows the initial model’s inability to accurately capture the data. The middle panel demonstrates the failure of the model without normalization. The right panel shows successful fitting after incorporating integral normalization.
More on tables
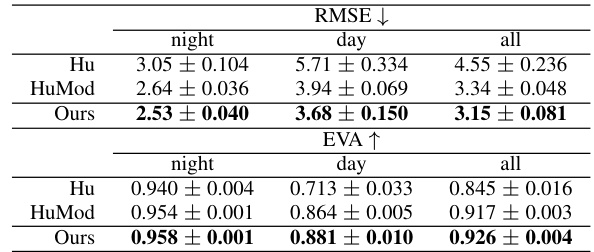
The table presents a comparison of motion deblurring and steering prediction performance metrics across different methods. The left side shows motion deblurring results using Mean Squared Error (MSE), Peak Signal-to-Noise Ratio (PSNR), and Structural Similarity Index Measure (SSIM). The right side presents steering prediction errors measured by Root Mean Squared Error (RMSE) and Explained Variance (EVA), categorized by day, night, and all conditions. The table highlights the performance improvements achieved by the proposed Parametric Piecewise Linear Networks (PPLNs) compared to existing state-of-the-art methods.

This table presents the results of human pose estimation and frame-based steering prediction experiments. The left side shows the 2D and 3D Mean Per Joint Position Errors (MPJPE) for human pose estimation, comparing the results of the proposed method against two baseline methods (Calabrese and CalabreseMod). The right side shows the Root Mean Squared Error (RMSE) and Explained Variance (EVA) for frame-based steering prediction, also comparing the proposed method to two baselines (Hu and HuMod). The results demonstrate the improved accuracy of the proposed method compared to the baselines in both tasks.

This table presents the results of ablation studies conducted to evaluate the impact of integral normalization on the performance of the proposed Parametric Piecewise Linear Networks (PPLNs). It compares the performance metrics (MSE, PSNR, SSIM for motion deblurring; RMSE, EVA for steering prediction; and 2D-2, 2D-3, 3D MPJPE for human pose estimation) with and without integral normalization. The results demonstrate the effectiveness of integral normalization in improving the overall performance across the three applications.

This table presents the 3D Mean Per Joint Position Error (MPJPE) in millimeters for a human pose estimation task. The results are broken down by movement type (33 total) and for five different subjects (S1-S5). The table also includes Calabrese’s original results and results from a modified version of Calabrese’s approach for comparison. The MPJPE represents the average error in estimating the 3D position of 13 key body joints. Lower values indicate better performance.

This table presents the 3D Mean Per Joint Position Error (MPJPE) in millimeters for a Spiking Neural Network (SNN) model evaluated on the Dynamic Vision Sensor Human Pose (DHP19) dataset. The results are broken down for 33 different movements and across 5 different subjects (S1-S5). The table shows the performance of the SNN model in estimating 3D human pose from event camera data.

This table presents the results of an ablation study conducted to determine the optimal number of line segments for the piecewise linear function in the PPLNs model, specifically for the steering prediction task. It shows that varying the number of segments (3, 6, 9, and 12) does not significantly improve performance. The metrics used for evaluation are Root Mean Squared Error (RMSE) and Explained Variance (EVA). The RMSE values indicate the average error in predicting the steering angle, while EVA reflects the proportion of variance in the steering angle that is explained by the model. Lower RMSE and higher EVA are desired, indicating better performance.

This table presents the ablation study results focusing on the impact of smoothing on the model performance. The results are categorized by three tasks: Motion Deblurring, Steering Prediction, and Human Pose Estimation. For each task, several metrics are reported, including Mean Squared Error (MSE), Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), Root Mean Square Error (RMSE), Explained Variance (EVA), and 2D/3D Mean Per Joint Position Error (MPJPE). The table compares the results obtained with and without smoothing, allowing for an assessment of the smoothing operator’s contribution to the overall model accuracy.
Full paper#



















