Activation Map Compression through Tensor Decomposition for Deep Learning

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in edge AI and deep learning due to its novel approach to compressing activation maps for efficient on-device training. It directly addresses the memory bottleneck in backpropagation, a major obstacle to deploying deep learning models on resource-constrained devices. The findings offer theoretical guarantees and demonstrate Pareto-superiority over existing methods, opening new avenues for on-device learning research and development.

Visual Insights

#

This figure illustrates the core concept of the proposed method: compressing activation maps to reduce memory usage during backpropagation. The left side shows the standard forward and backward passes, where activation maps (A_i and A_i+1) are stored in memory. The right side shows how the proposed method compresses these activation maps before storing them, reducing memory usage while allowing for efficient reconstruction when needed for backpropagation. The compression process is represented by the symbol of a double arrow with a smaller width than the other arrows to indicate that it is using a lossy compression technique. The gears represent the computation process.

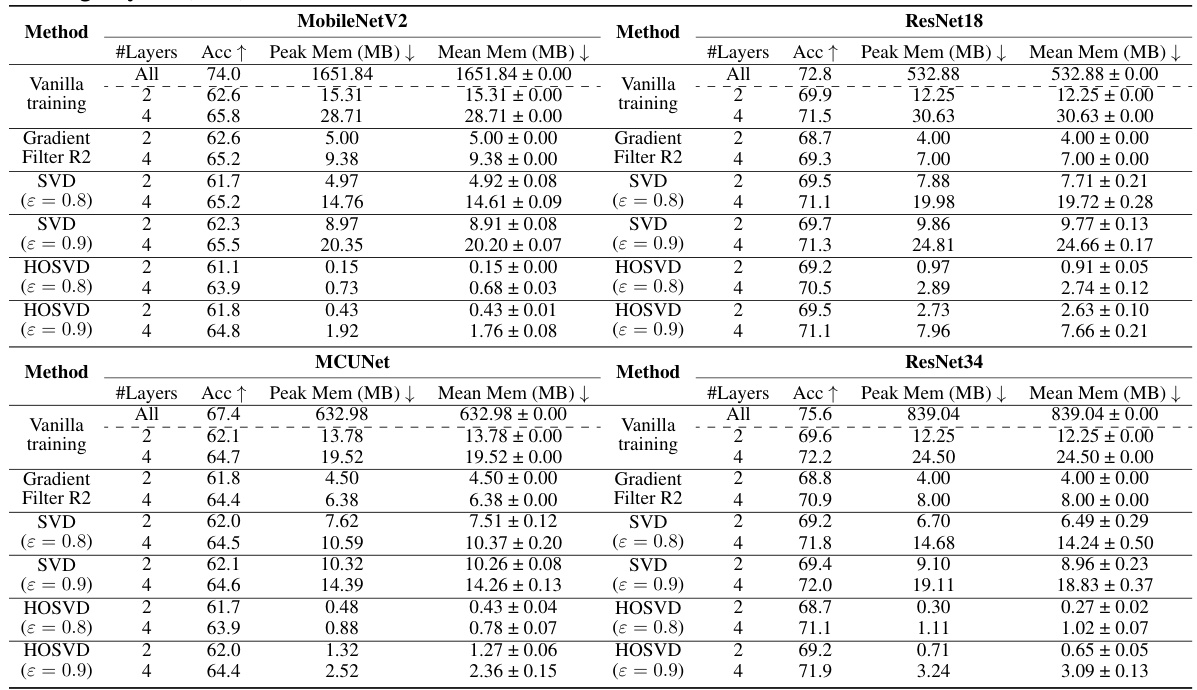
This table presents the classification performance and memory consumption for MobileNetV2, ResNet18, and ResNet34 models. It shows the top-1 validation accuracy and peak/mean activation memory (in MB) for different fine-tuning setups (varying the number of fine-tuned layers): Vanilla training, Gradient Filter (with different patch sizes), SVD (with ε = 0.8 and ε = 0.9), and HOSVD (with ε = 0.8 and ε = 0.9). The results demonstrate the trade-off between accuracy and memory consumption for different methods and the impact of fine-tuning different numbers of layers.

In-depth insights

#

Edge AI Bottleneck

#

The core bottleneck in Edge AI is the constrained computational resources of edge devices. Unlike cloud-based AI, edge devices have limited processing power, memory, and energy. This severely restricts the complexity of models that can be deployed, hindering performance for demanding applications like real-time object detection or complex image processing. Furthermore, the memory footprint of activation maps during backpropagation represents a significant challenge. Storing these maps consumes substantial memory, often exceeding the available resources on edge devices. This limits the feasibility of on-device training, which is crucial for adapting models to evolving data distributions and ensuring data privacy. Therefore, effective Edge AI necessitates innovative techniques to compress model parameters and activation maps, thereby reducing computational and memory demands while maintaining accuracy. Successful Edge AI strategies require a careful balance between model complexity, performance, and resource efficiency.

Tensor Decomposition

#

Tensor decomposition methods are explored as a powerful technique for compressing activation maps in deep learning models. This compression is crucial for enabling efficient on-device training, overcoming the memory limitations of embedded systems. Singular Value Decomposition (SVD) and its higher-order variant, Higher-Order SVD (HOSVD), are investigated and compared. These methods reduce the memory footprint of activations without sacrificing the essential features needed for effective learning. The approach offers theoretical guarantees on convergence, and experimental results demonstrate significant memory savings while maintaining performance, offering a Pareto-superiority compared to existing approaches. The core idea revolves around using low-rank approximations to capture the majority of tensor variance, thus allowing for efficient backpropagation. The trade-off between compression ratio and performance is carefully analyzed.

HOSVD Backprop

#

The concept of “HOSVD Backprop” centers on accelerating and making memory-efficient the backpropagation process in deep learning, particularly for on-device training. It leverages High-Order Singular Value Decomposition (HOSVD) to compress activation maps, significantly reducing memory requirements. This compression is crucial for resource-constrained environments like embedded systems or IoT devices. The method’s core strength lies in its ability to maintain accuracy despite compression, achieved by adaptively capturing the majority of tensor variance. Theoretical guarantees of convergence are a significant advantage. This approach isn’t limited to specific network architectures, offering broad applicability and flexibility. The method’s effectiveness has been demonstrated through experiments, showing a considerable improvement in the trade-off between accuracy and memory footprint when compared to traditional backpropagation and other state-of-the-art compression techniques. The use of HOSVD is particularly beneficial for high-dimensional activation tensors.

Compression Tradeoffs

#

The core concept of ‘Compression Tradeoffs’ in the context of deep learning revolves around the inherent conflict between achieving high model compression and maintaining optimal performance. Higher compression rates generally lead to smaller model sizes, reduced memory usage, and faster inference times, which are highly desirable for resource-constrained environments like edge devices. However, excessive compression often results in information loss, which can negatively impact the model’s accuracy and generalization capabilities. The sweet spot lies in finding the best balance: sufficient compression to meet resource constraints without significantly compromising performance. This optimization process, the exploration of compression trade-offs, is crucial for successfully deploying deep learning models in real-world applications, especially where computational resources are limited. The optimal trade-off point is often context-dependent, varying based on the specific application requirements (accuracy needs, hardware limitations) and the nature of the data itself. Effective strategies for managing compression trade-offs involve the careful selection and tuning of compression techniques (e.g., pruning, quantization, knowledge distillation, tensor decomposition) to maximize performance within acceptable resource limits.

Future of On-Device

#

The “Future of On-Device” in deep learning hinges on solving the computational and memory constraints of resource-limited devices. Current research focuses on model compression techniques, such as tensor decomposition, to reduce the memory footprint of activation maps during backpropagation. On-device training is crucial for adapting models to real-world data drift and ensuring privacy, but requires efficient gradient computation methods. Future advancements will likely involve further exploration of low-rank approximation algorithms, novel backpropagation techniques, and hardware acceleration. Continual learning strategies are vital for enabling on-device models to adapt and improve their performance over time, reducing reliance on cloud-based training and maintaining accuracy in dynamic environments. The key challenge will be finding the optimal balance between model accuracy, computational efficiency, and memory usage on embedded systems, leading to more robust and versatile edge AI applications.

More visual insights

#

More on figures

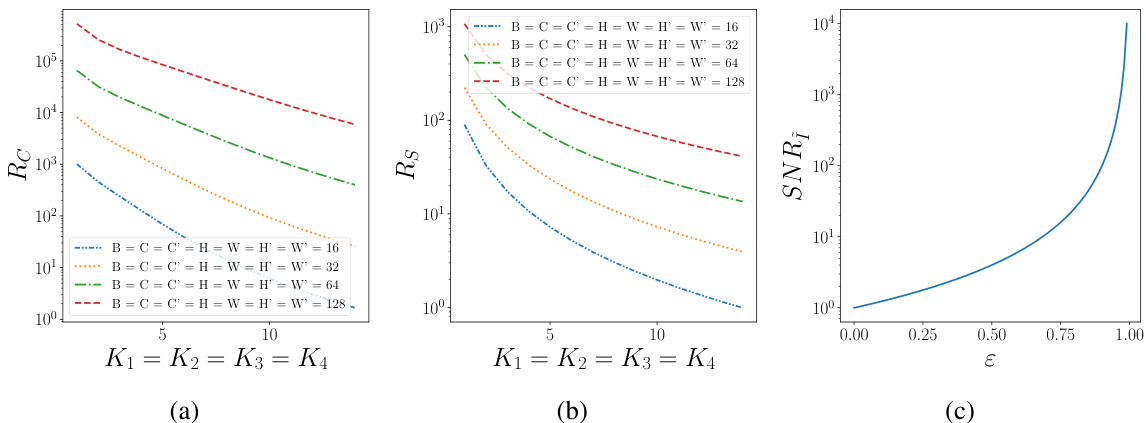
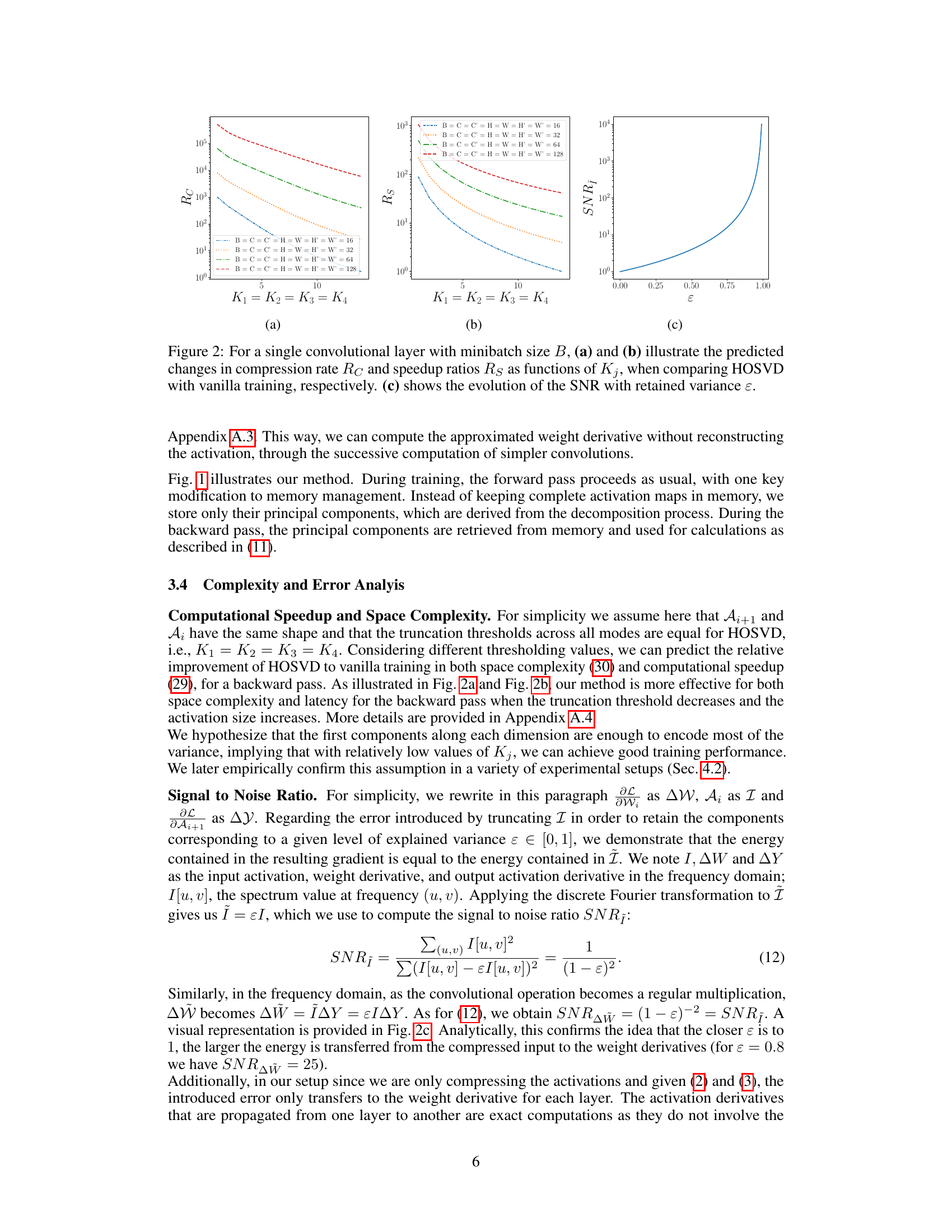
This figure shows the predicted performance of HOSVD compared to vanilla training for a single convolutional layer. Subfigure (a) shows the compression rate (Rc) as a function of the number of principal components (Kj) kept after applying HOSVD. Subfigure (b) displays the speedup ratio (Rs) achieved by using HOSVD versus vanilla training, also as a function of Kj. Subfigure (c) illustrates the relationship between the signal-to-noise ratio (SNR) and the retained variance (ε) when applying HOSVD. This figure demonstrates that HOSVD offers significant compression and speedup advantages while maintaining acceptable SNR.

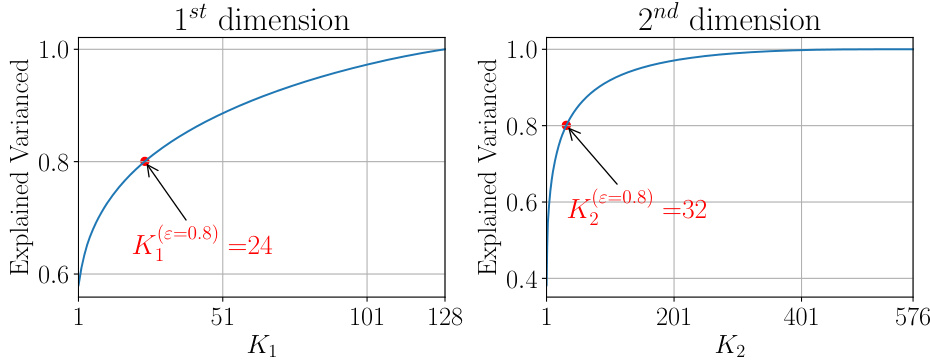
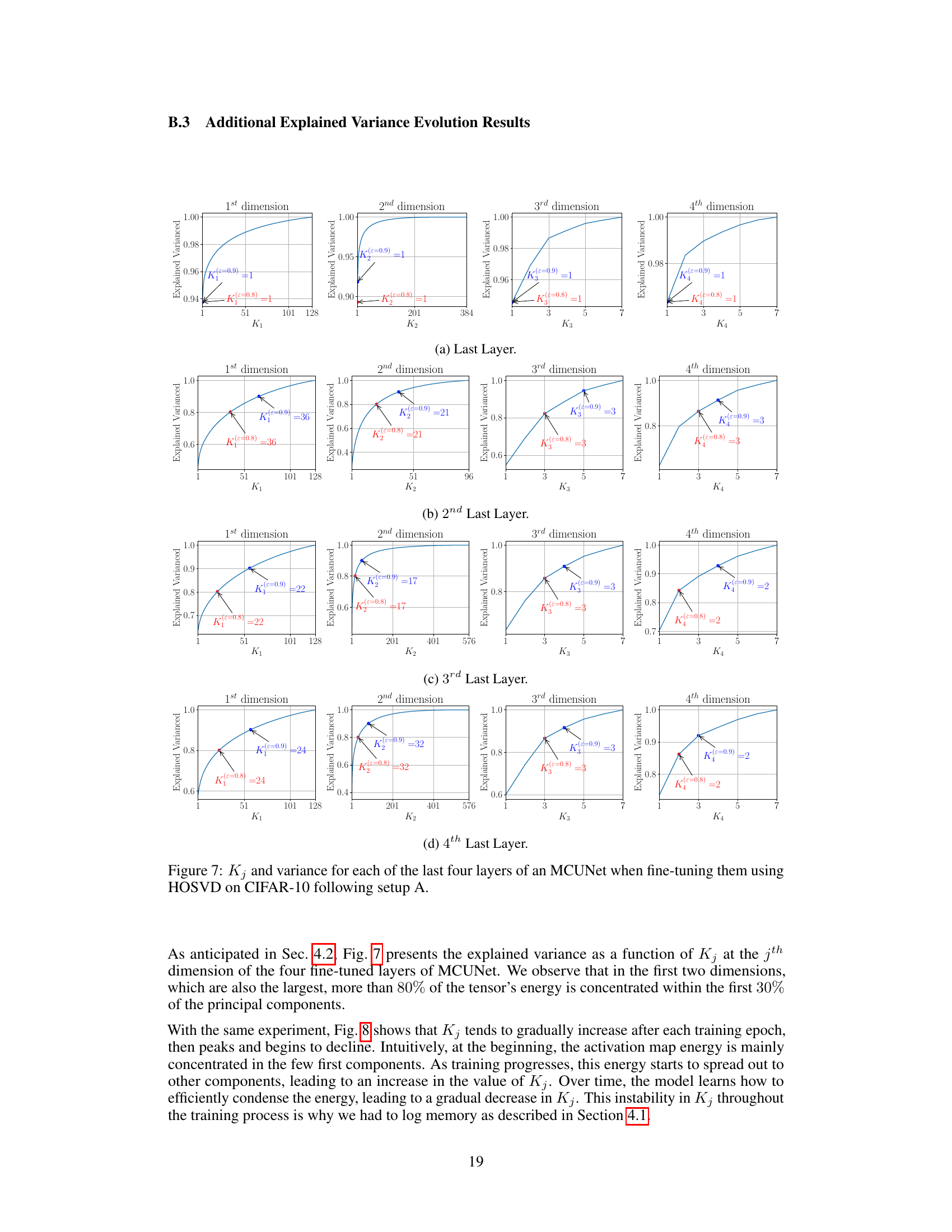
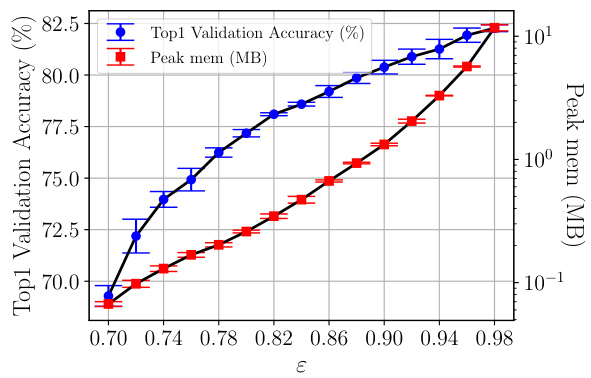
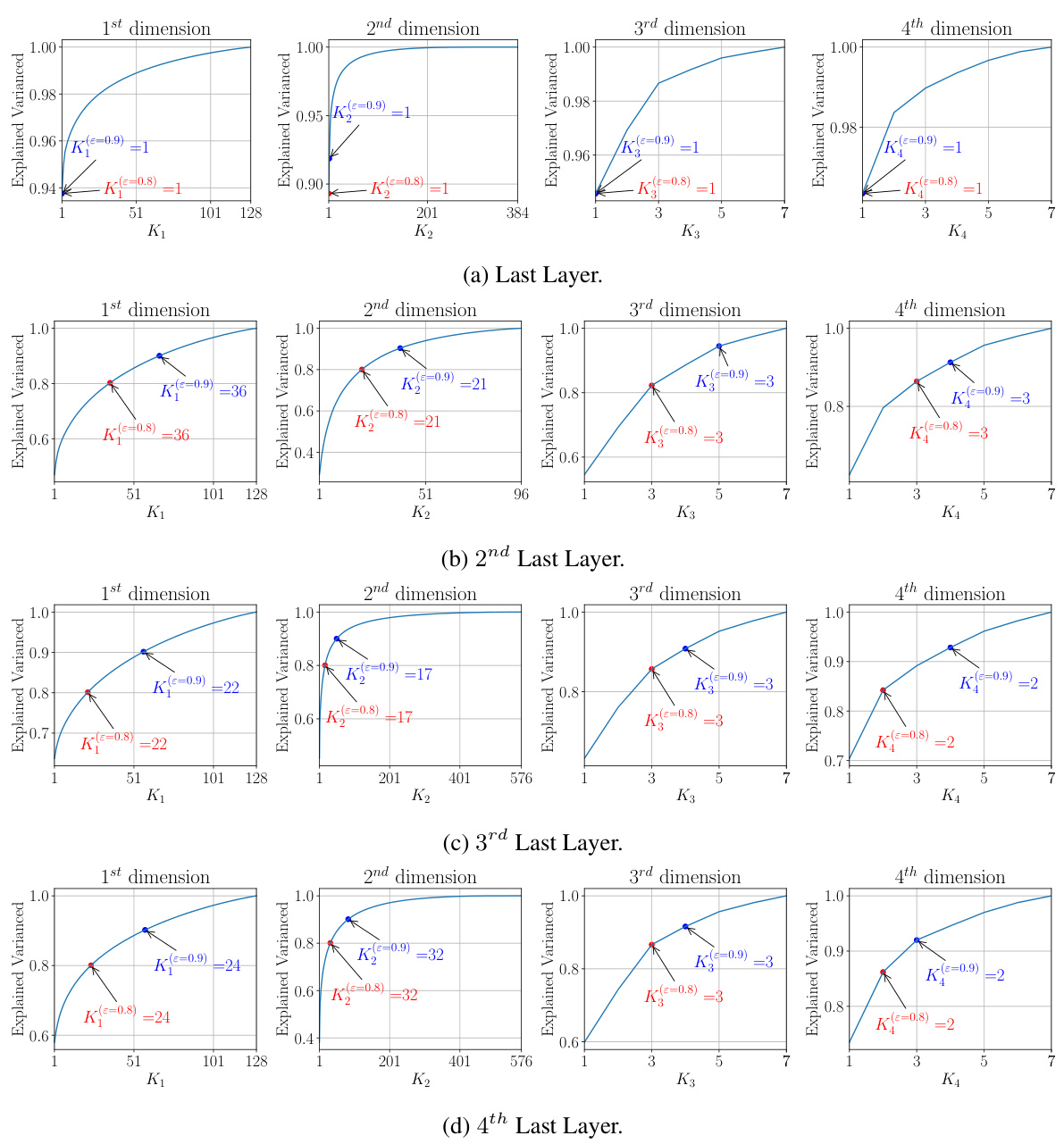
This figure shows the explained variance for the first two dimensions of the activation map in the 4th last layer of a MCUNet model when fine-tuning the last four layers using HOSVD on the CIFAR-10 dataset. It illustrates how many principal components (K1 and K2) are needed to retain a specific fraction (ε=0.8) of the explained variance in each dimension. The plot indicates that a relatively small number of principal components can capture a significant portion of the variance.

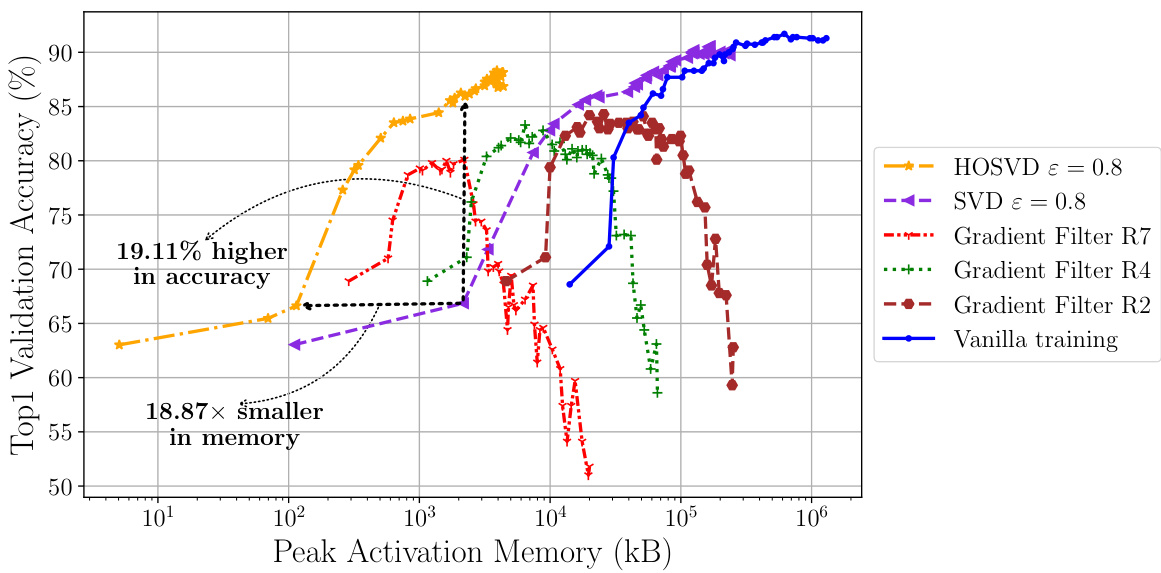
This figure shows the performance of different activation compression techniques on a MCUNet model. The x-axis represents the peak activation memory in kilobytes, while the y-axis represents the top-1 validation accuracy. The plot compares vanilla training to several compression methods, including HOSVD and SVD with different variance thresholds, and gradient filtering with different patch sizes. The results demonstrate that HOSVD achieves higher accuracy with significantly lower memory compared to other methods, highlighting its effectiveness for memory-constrained environments. Specific values are highlighted showing the improvement of HOSVD over vanilla training in accuracy and memory reduction.

This figure shows the performance of different activation compression strategies when fine-tuning a MCUNet model. The model is first pre-trained on ImageNet and then fine-tuned on CIFAR-10. The x-axis represents the peak activation memory in kilobytes (kB), while the y-axis represents the top-1 validation accuracy. Multiple lines represent different strategies: vanilla training (no compression), gradient filtering with different patch sizes (R2, R4, R7), SVD (singular value decomposition), and HOSVD (higher-order singular value decomposition) with an explained variance threshold of 0.8. The graph illustrates the trade-off between memory usage and accuracy for each method. HOSVD demonstrates superior performance in terms of achieving higher accuracy with significantly less memory compared to other methods, highlighting its effectiveness for memory-constrained environments.

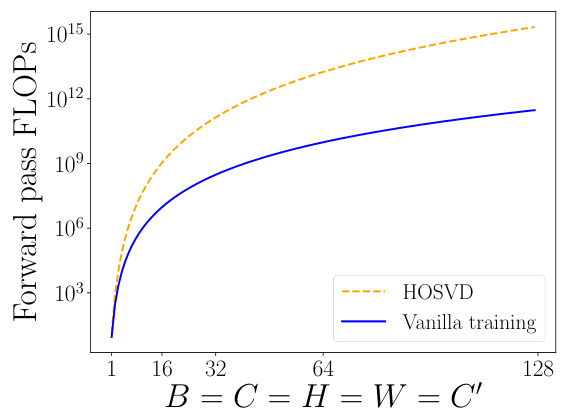
This figure shows the predicted FLOPs (floating point operations) for the forward pass of a convolutional layer during training. The blue line represents vanilla training, while the orange dashed line represents the proposed HOSVD method. The x-axis shows the increasing size of the activation map (B=C=H=W=C’). The plot demonstrates that vanilla training’s FLOPs increase more slowly than HOSVD’s with increasing activation map size. The HOSVD method has significantly higher FLOPs than Vanilla at smaller activation map sizes but eventually the difference becomes relatively small.

This figure shows the predicted effects of using Higher Order Singular Value Decomposition (HOSVD) for activation map compression on a single convolutional layer. Subfigure (a) illustrates the predicted compression rate (Rc) as a function of the number of principal components (Kj) kept in each mode of the tensor decomposition, comparing HOSVD to the standard training method (vanilla). Subfigure (b) shows the predicted speedup ratio (Rs) achieved by HOSVD over the standard training method. Finally, subfigure (c) shows the Signal-to-Noise Ratio (SNR) in relation to retained variance (ε), indicating how well the variance is captured with compression.

This figure shows the predicted changes in compression rate and speedup ratios when using HOSVD compared to vanilla training for a single convolutional layer. Different values of Kj (the number of principal components kept in each mode of the tensor decomposition) are used to demonstrate how the compression rate and speedup vary. The graphs show that higher compression rates and speedup are achieved with smaller values of Kj. Finally, another graph illustrates the relationship between the Signal-to-Noise Ratio (SNR) and retained variance ε, showing that the SNR increases quadratically with retained variance.

This figure illustrates the trade-off between peak activation memory (in kilobytes) and top-1 validation accuracy (%) for different activation compression methods on the MCUNet model. The model was pre-trained on ImageNet and fine-tuned on CIFAR-10. The plot compares vanilla training with various compression techniques including HOSVD (Higher-Order Singular Value Decomposition), SVD (Singular Value Decomposition), and Gradient Filter with different compression ratios. The results show that HOSVD achieves a better balance between high accuracy and low memory compared to other methods.

More on tables

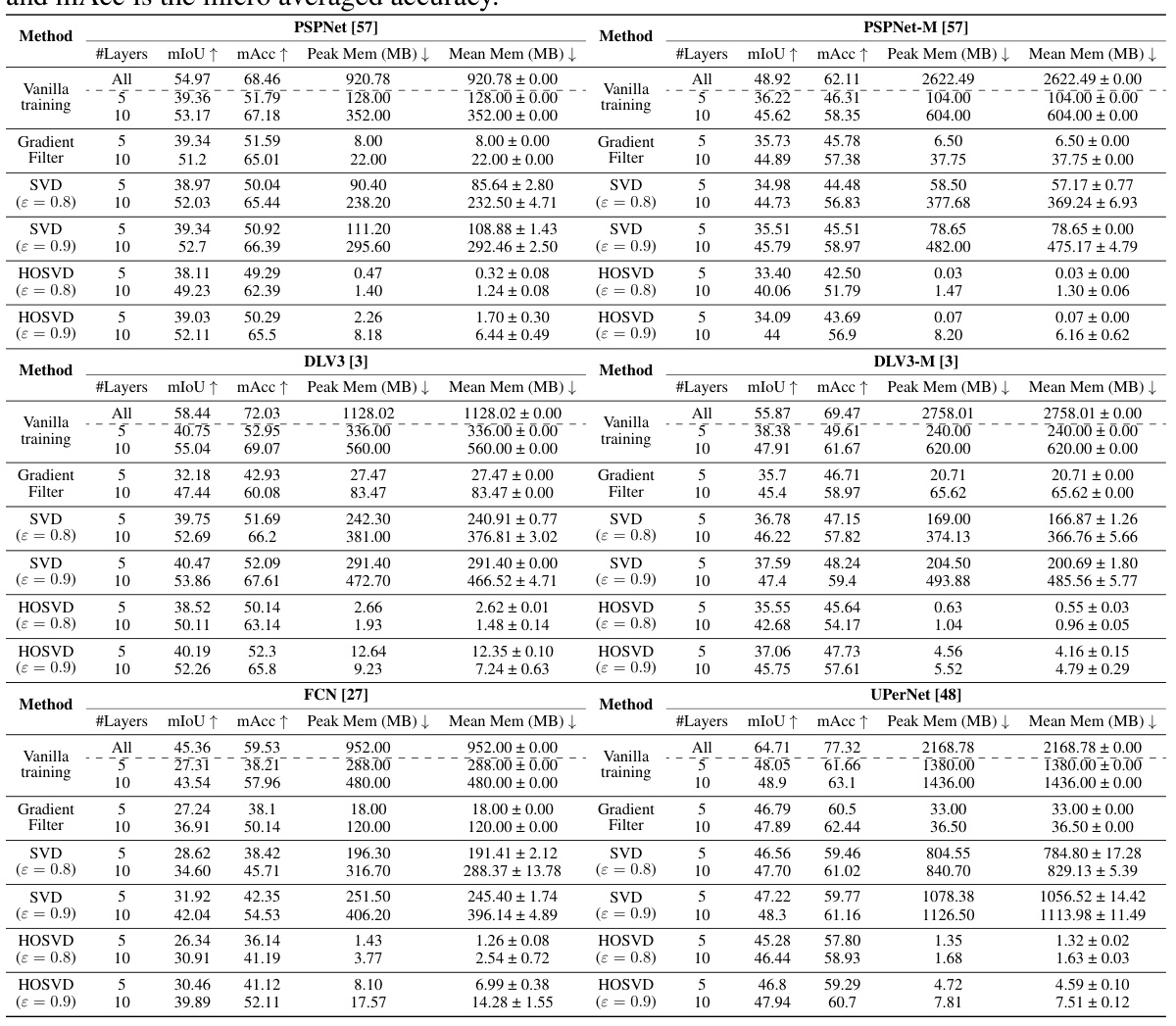
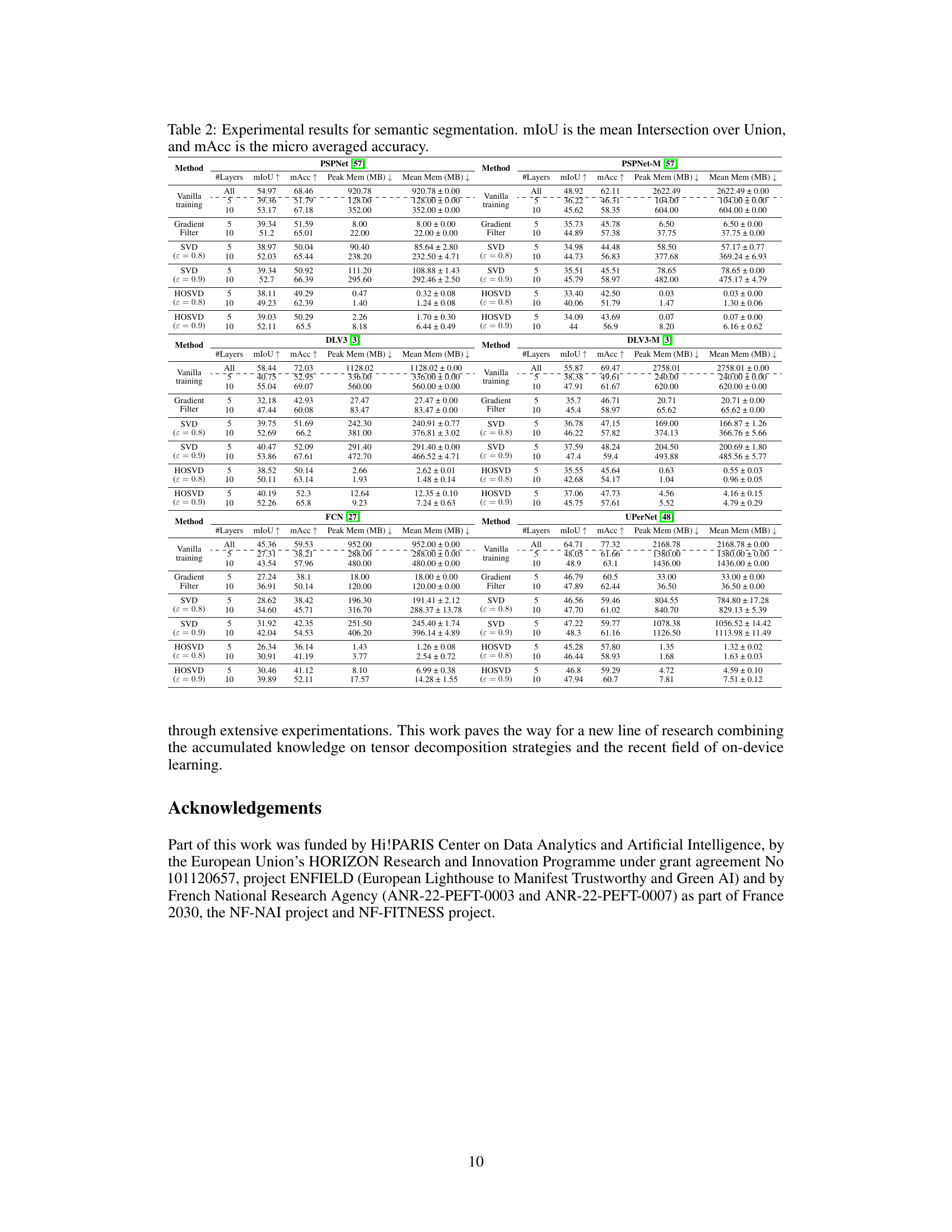
This table presents the results of semantic segmentation experiments using different methods (Vanilla training, gradient filtering, SVD, and HOSVD) on various models (PSPNet, PSPNet-M, DLV3, DLV3-M, FCN, and UPerNet). For each model and method, the mean Intersection over Union (mIoU), micro-averaged accuracy (mAcc), peak memory usage, and mean memory usage are reported for different numbers of fine-tuned layers (5 and 10). The results show the trade-off between model accuracy and memory consumption achieved using different compression techniques.

This table presents the results of semantic segmentation experiments using the DeepLabV3 model with different random seeds. It shows the mean intersection over union (mIoU) and micro-averaged accuracy (mAcc) for different numbers of layers (5 and 10) and different methods (HOSVD and SVD with ε = 0.8). The standard deviations are also provided for each metric.

This table shows the experimental results of fine-tuning different numbers of layers on ImageNet-1k using various methods including vanilla training, gradient filtering, SVD, and HOSVD. The table presents the top-1 validation accuracy and activation memory (peak and mean) in MB for MobileNetV2, ResNet18, ResNet34, and SwinT models.

Full paper

#